【数论】最大公约数、约数的个数与约数之和定理
Halo,这里是Ppeua。平时主要更新C语言,C++,数据结构算法......感兴趣就关注我吧!你定不会失望。
🌈个人主页:主页链接
🌈算法专栏:专栏链接
我会一直往里填充内容哒!
🌈LeetCode专栏:专栏链接
目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目,也会当天做完发出
🌈代码仓库:Gitee链接
🌈点击关注=收获更多优质内容🌈
用辗转相除法求最大公约数,以及数论相关的知识:约数个数与约数和的定理,及代码实现
目录
题目:最大公约数
题解:
代码实现:
题目:约数个数
题解:
代码实现:
题目:约数之和
题解:
代码实现:
完结撒花:
先来科普下什么是约数:当a能被b整除,我们就说b为a的约数,b的倍数为a
题目:最大公约数

题解:
这里我们用到了辗转相除法 先读入a与b这两个数,之后把a与b相除,令其结果为c,若c不为0,则令a=b,b=c(辗转就是体现在了这里),若c为0,则说明b为a的最大公约数,则输出b即可
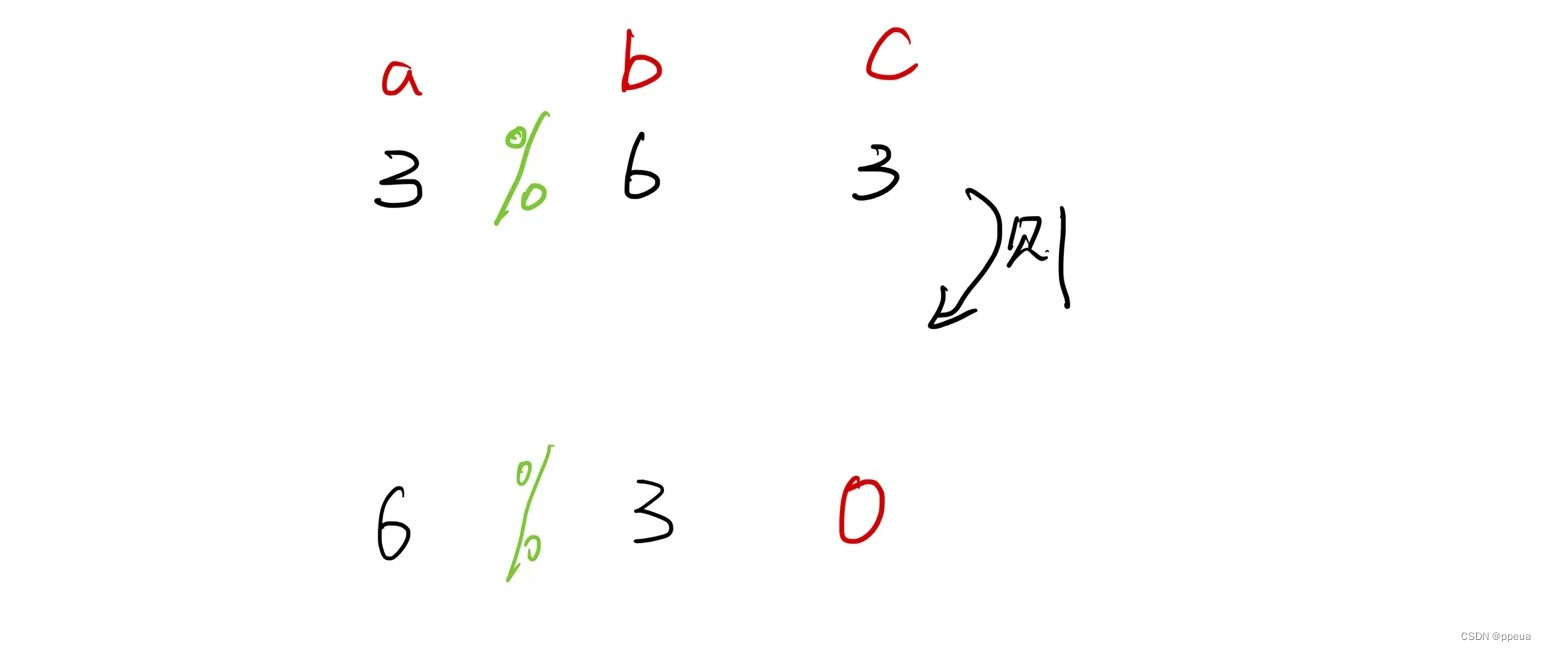
代码实现:
#include<iostream>
using namespace std;
int gcd(int a,int b)
{return b?gcd(b,a%b):a;
}
int main()
{int n=0;cin>>n;while(n--){int a,b;cin>>a>>b;cout<<gcd(a,b)<<endl;}return 0;
}题目:约数个数
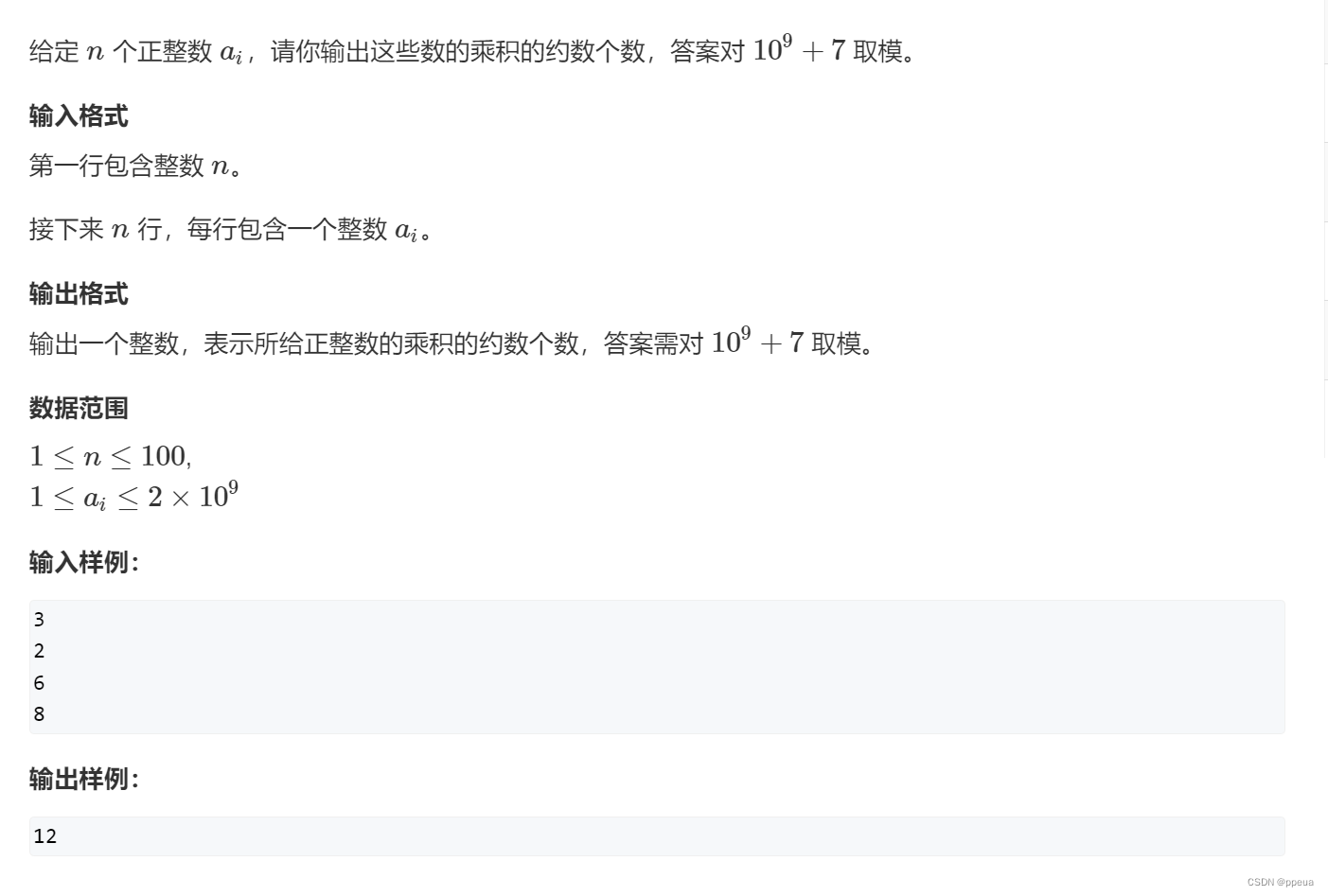
题解:
这里先科普一个数学知识,约数个数定理,假设这个数为16,求出他的质因子为2,其指数为4
那么其约数的个数就为指数加一(4+1)
可以这样理解
第一个约数为其因子的1次方2,第二个约数为其因子的二次方2*2
第三个约数为其因子的三次方2*2*2
第四个约数为其因子的四次方2*2*2*2 第五个约数为其因子的0次方也就是1

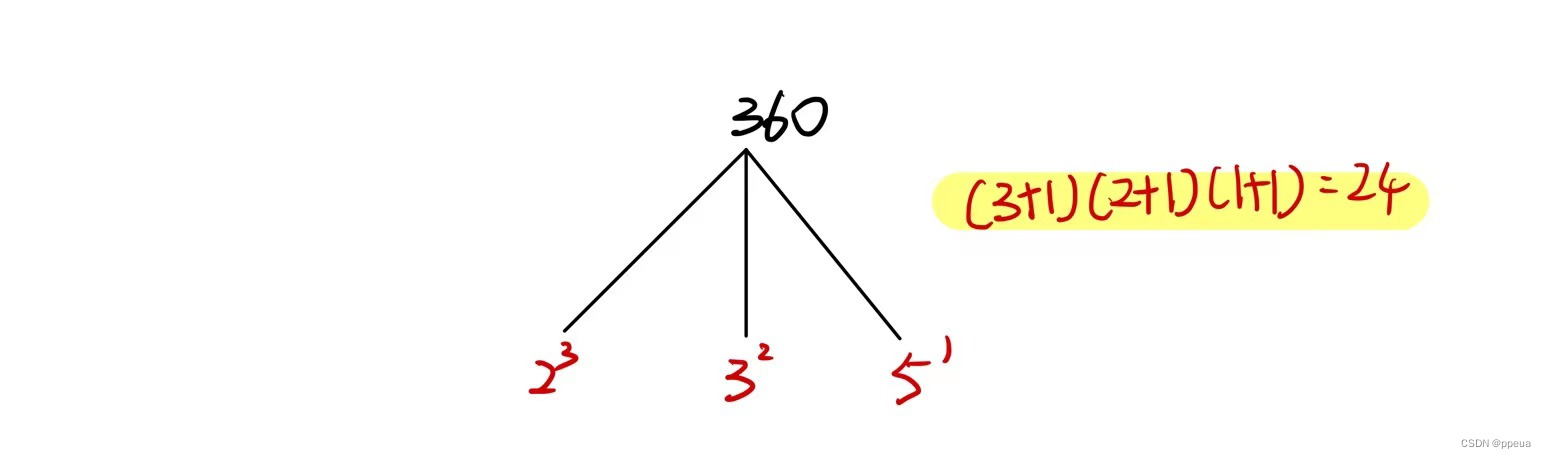
再举一个例子:
所以360的约数个数就为(3+1)*(2+1)*(1+1)
这就是约数个数定理
回顾一下 我们要做的就是将一个数求出他每一个质因子(不会的uu们可以看看这篇文章分解质因数)并记录其指数情况。之后将指数拿出来做乘法就ok了
这里用hash表记录其质因子与指数的情况,其中key为质因子 value为指数,所以最后的表达式就为指数value,所以最后就将其加一再相乘即可。
代码实现:
#include<iostream>
#include<unordered_map>
using namespace std;
const int N=1e9+7;
int main()
{unordered_map<int,int>map;int n=0,s;cin>>s;while(s--){cin>>n;for(int i=2;i<=n/i;i++){while(n%i==0){n/=i;map[i]++;}}if(n>1)map[n]++;}long long res=1;for(auto ma:map){long long p=1;int a=ma.second;res=(res*(a+1))%N;}cout<<res;
}题目:约数之和
题解:
上面学了约数个数的定理,现在我们再来学一下约数之和定理,同样非常的简单
仍然以16来举例子,其质因子为2指数为4.
所以其约数之和为(2^0+2^1+2^2+2^3+2^4)=31
再来举上面360的例子:
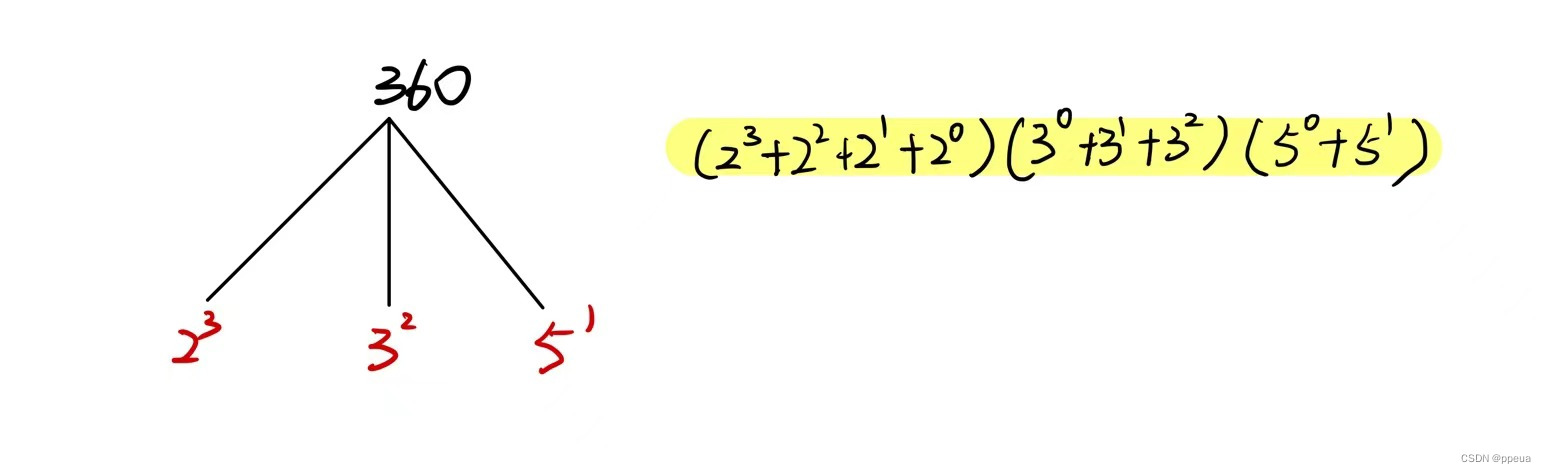
所以其约数之和为1261
这就是约数之和定理。
回顾一下 我们要做的就是将一个数求出他每一个质因子(不会的uu们可以看看这篇文章分解质因数)并记录其指数情况。之后将其拿出来先相加再做乘法就ok了
这里用hash表记录其质因子与指数的情况,其中key为质因子 value为指数,所以最后的表达式就为指数value与其质因子,先相加再相乘就好。
代码实现:
#include<iostream>
#include<unordered_map>
using namespace std;
const int N=1e9+7;
int main()
{unordered_map<int,int>map;int n=0,s;cin>>s;while(s--){cin>>n;for(int i=2;i<=n/i;i++){while(n%i==0){n/=i;map[i]++;}}if(n>1)map[n]++;}long long res=1;for(auto ma:map){long long p=1;int a=ma.second;while(a--)p=(p*ma.first+1)%N;res=res*p%N;}cout<<res;
}完结撒花:
🌈本篇博客的内容【数论:最大公约数、约数的个数与约数之和定理】已经结束。
🌈若对你有些许帮助,可以点赞、关注、评论支持下博主,你的支持将是我前进路上最大的动力。
🌈若以上内容有任何问题,欢迎在评论区指出。若对以上内容有任何不解,都可私信评论询问。
🌈诸君,山顶见!
相关文章:
【数论】最大公约数、约数的个数与约数之和定理
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
)
第28篇:Java日期Calendar类总结(二)
目录 1、获取系统当前时间 2、获取指定日期 3、对象字段类型 4 、对象信息设置 4.1 Set设置...

【Python】字符串 - 集大成篇
目录 1. 不同语言的字符串比较 1.1 C 语言 1.2 C 语言 1.2.1 C 风格字符串 1.2.2 C 风格字符串 1.3 JAVA 1.4 Python 2. Python 字符串 2.1 方法 2.2.1 title () 2.2.2 lower () 2.2.3 upper () 2.2.4 rstrip () 2.2.5 lstrip …...

IDEA: 如何导入项目模块 以及 将 Java程序打包 JAR 详细步骤
IDEA: 如何导入项目模块 以及 将 Java程序打包 JAR 详细步骤 、 文章目录IDEA: 如何导入项目模块 以及 将 Java程序打包 JAR 详细步骤IDEA 导入项目模块 Module一. 创建一个空项目二. 导入 Module三. 将 Module 与 当前项目关联上IDEA 将 Java程序打包成…...
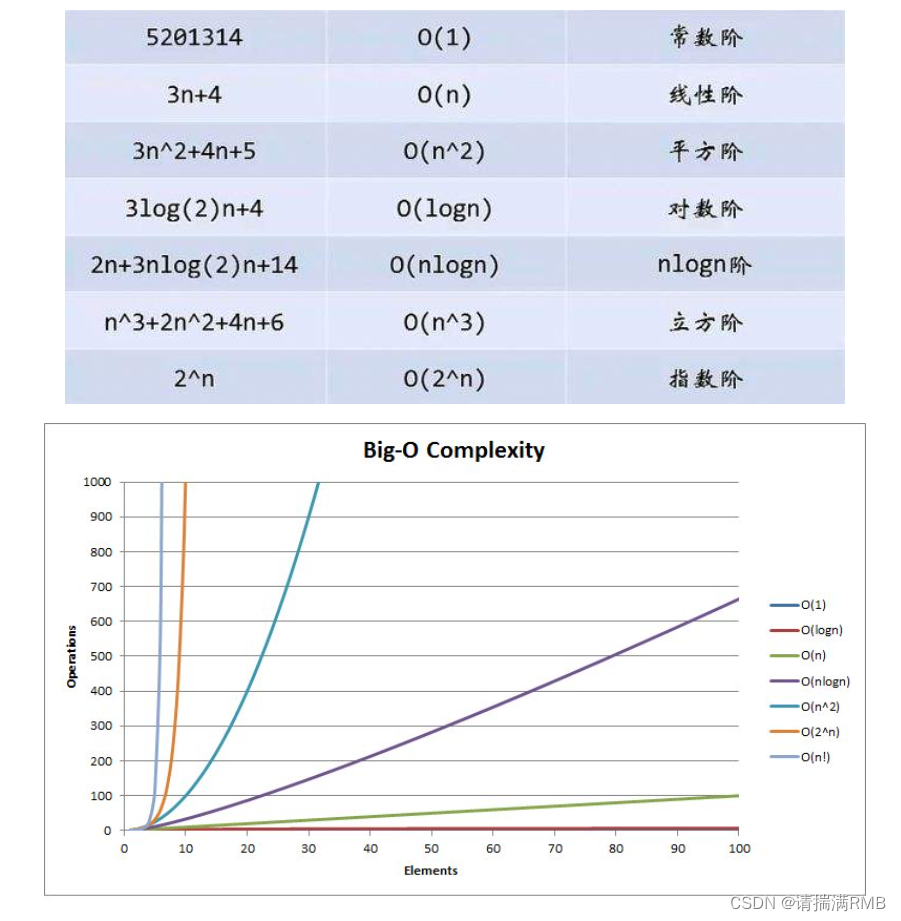
算法的效率——时间复杂度和空间复杂度
文章目录1. 算法效率1.1 什么是算法1.2 算法的好坏2. 时间复杂度2.1 什么是时间复杂度2.2 时间复杂度的计算方法2.3 大O的渐进表示法2.4 常见时间复杂度计算举例3. 空间复杂度4. 常见复杂度对比1. 算法效率 1.1 什么是算法 目前普遍认可对算法的定义是:算法是解决…...

2021年 第12届 蓝桥杯 Java B组 省赛真题详解及小结【第1场省赛 2021.04.18】
总分:5 一、试题A:ASC 得分:5分 本题总分:5 分 【问题描述】 已知大写字母 A 的 ASCII 码为 65,请问大写字母 L 的 ASCII 码是多少? 【答案提交】 这是一道结果填空的题,你只需要算出结果后提…...
透过等待看数据库
等待分类与解决基本流程步骤1.定位问题系统等待往往能直观的反映出系统问题。通过一些常见的等待类型,同样可以找到系统瓶颈,结合性能计数器往往定位更准确。如:系统中存在大量IO类等待,那么可能表示你的磁盘或内存是语句运行缓慢…...
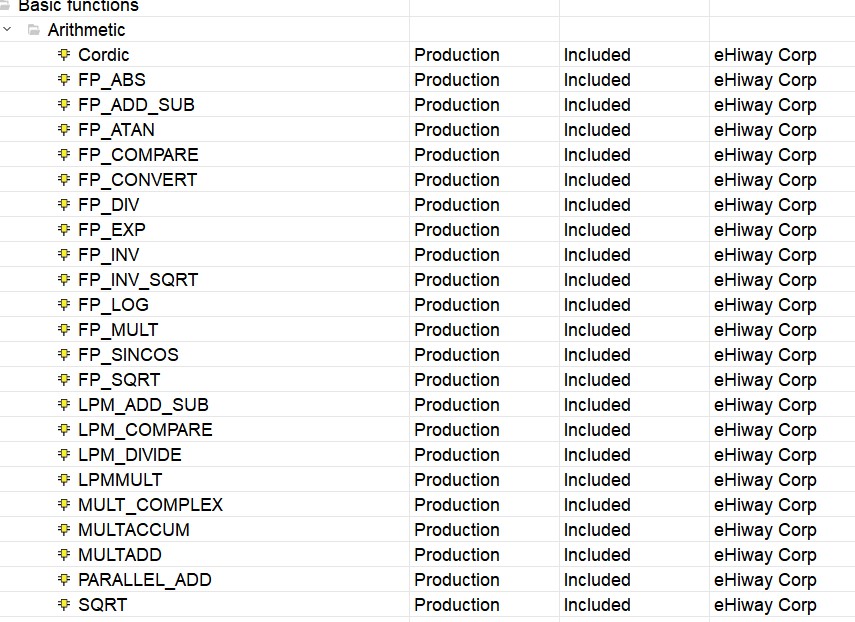
中科亿海微FPGA
国产FPGA中,紫光、安路、高云称得上是三小龙,其他的半斤八两,中科亿海微也算是其中之一。 其产品为亿海神针系列,如下: 可见其最小规模也有9.2KLUT,最大竟有136K之多了,对比其他国产࿰…...

【链表OJ题(三)】链表中倒数第k个结点
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录链表OJ题(三)1. 链表…...

华为防火墙的学习
防火墙 - 含义和定义 什么是防火墙? 防火墙的工作原理 防火墙的区域: 包过滤防火墙----访问控制列表技术---三层技术 代理防火墙----中间人技术---应用层 状态防火墙---会话追踪技术---三层、四层 UTM---深度包检查技术----应用层 下一代防火墙 防火墙的…...
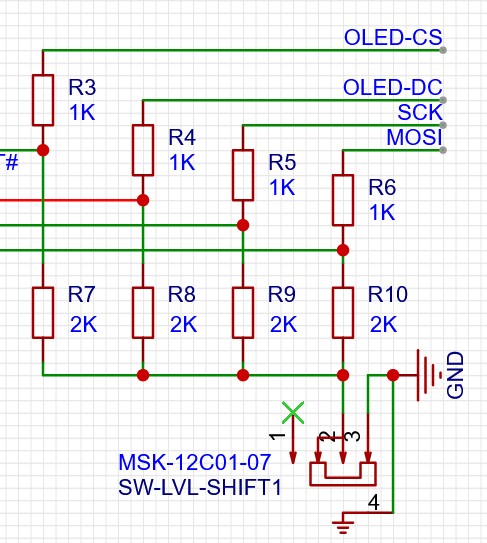
SPI 接口OLED 模块 - 兼容5V 和3.3V 电平
PCB 布局参考了老王0.8元128x32OLED显示屏转接板,开源项目地址:老王0.8元128x32OLED。 老王家买的屏幕放了快一年了,终于还是决定整个单独的模块,之前一直打算集成到开发板上的,不太灵活。相比那个转接板,主…...

css布局和定位
在Web开发中,CSS布局和定位是非常重要的技能。在这篇博客中,我们将深入探讨CSS布局和定位的概念、基本技术和最佳实践。 **CSS布局基础** ├── 盒模型 │ ├── 内边距 │ │ ├── padding │ │ ├── padding-top │ │ ├── p…...
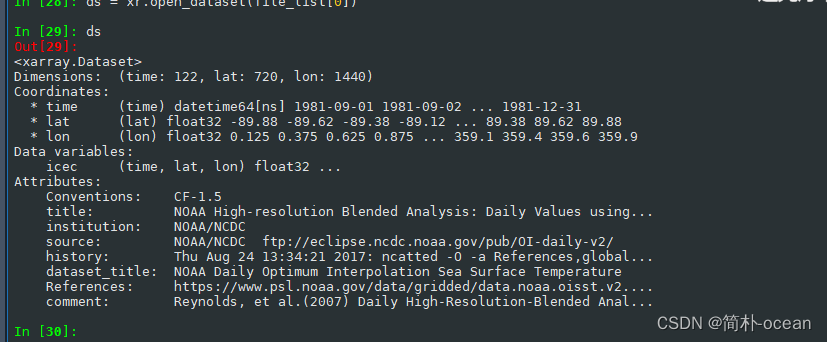
python -- 批量读取多个文件,并将每个文件中相同变量累加
python – 批量读取多个文件,并将每个文件中相同变量累加 情况描述 现有多个nc文件,位于同一个文件夹中,如下所示每个文件中都有相同的变量,想要读取每个文件中的变量然后将其加起来意思就是说: 文件1中的变量文件2中…...

低代码开发流程是怎么样的?
低代码开发流程是怎么样的?现在很多文章都在下功夫宣传what(低代码是什么)、why(为什么要用低代码),但是很少有文章能够系统讨论how(怎么用低代码)的问题。 所以我花3天的时间准备了…...

任何时候都不要在 for 循环中删除 List 集合元素!!!
首先说结论:无论什么场景,都不要对List使用for循环的同时,删除List集合元素,因为这么做就是不对的。 阿里开发手册也明确说明禁止使用foreach删除、增加List元素。 正确删除元素的方式是使用迭代器(Iteratorÿ…...

koa+Vite+vue3+ts+pinia构建项目
一、 初始化构建项目 npm create vite myProject -- --template vue-ts 注:Vite 需要 Node.js 版本 14.18,16。然而,有些模板需要依赖更高的 Node 版本才能正常运行,当你的包管理器发出警告时,请注意升级你的 Node 版…...
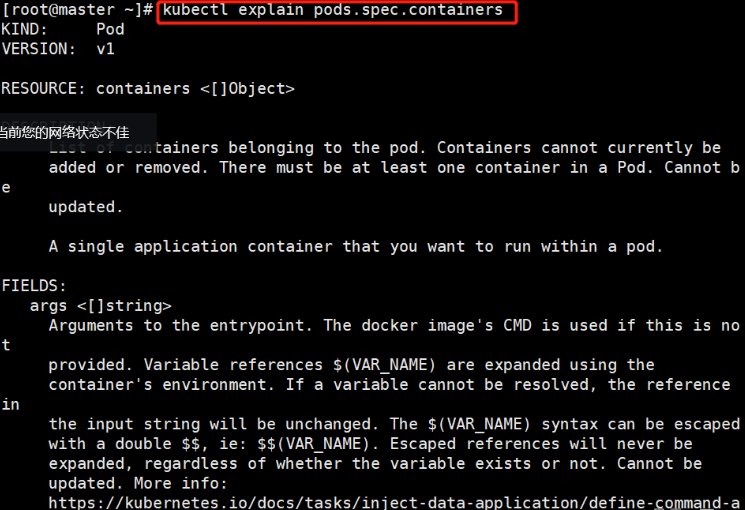
k8s-yaml文件
文章目录一、K8S支持的文件格式1、yaml和json的主要区别2、YAML语言格式二、YAML1、查看 API 资源版本标签2、编写资源配置清单2.1 编写 nginx-test.yaml 资源配置清单2.2 创建资源对象2.3 查看创建的pod资源3、创建service服务对外提供访问并测试3.1 编写nginx-svc-test.yaml文…...
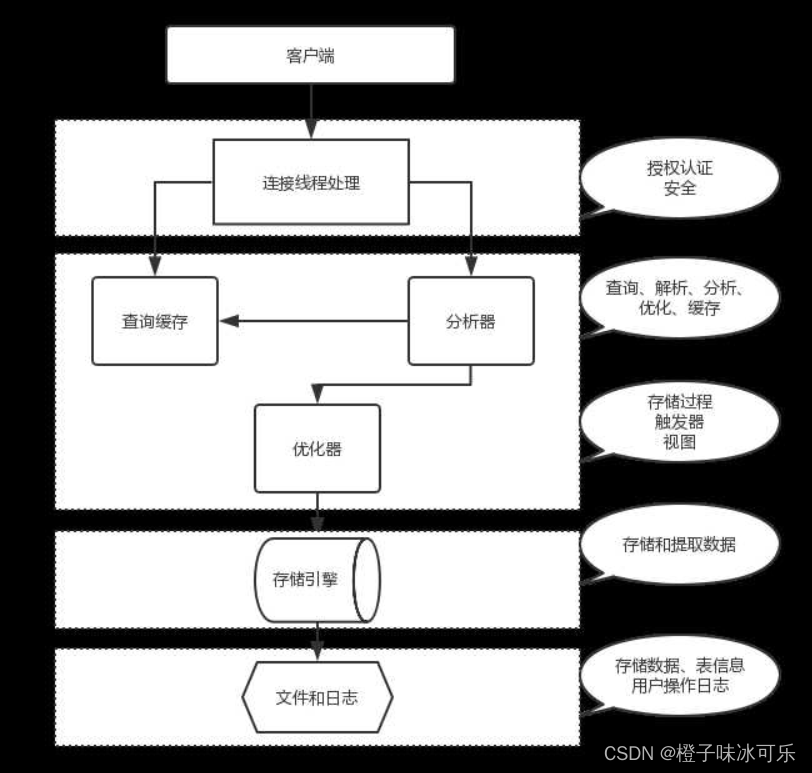
存储引擎
目录 ❤ MySQL存储引擎 什么是存储引擎? MySQL支持哪个存储引擎? ❤ 各种存储引擎的特性 概述 各种存储引擎的特性 各种搜索引擎介绍 ❤ 常用存储引擎及适用场景 ❤ 存储引擎在mysql中的使用 存储引擎相关sql语句 指定存储引擎建表 在建表时指定 在配置文件中…...

Go中 channel的使用
文章目录背景channel 简介使用说明声明发送和接受数据关闭channel使用示例背景 使用 sync 包和 context 包的工具可以实现多个协程之间互相协作, 但是没有一种很好的方式解决多个协程之间通信的问题. golang 作者 Rob Pike 说过一句话,不要通过共享内存来通信&…...

【C++】string OJ练习
文章目录1. 仅仅反转字母思路分析代码实现2. 字符串中的第一个唯一字符题目分析代码实现3. 《剑指offer》——替换空格解法一:寻找替换思路分析代码实现优化解法二:空间换时间思路分析代码实现4.字符串最后一个单词的长度思路分析代码实现5. 字符串相加思…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

