layui项目中的layui.define、layui.config以及layui.use的使用
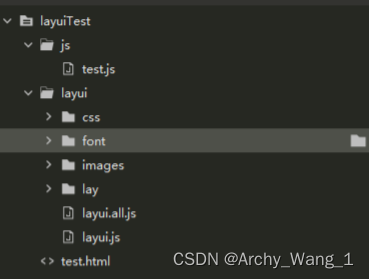
第一步:创建一个layuiTest项目,结构如下
第二步:新建一个test.js,利用layui.define定义一个模块test,并向外暴露该模块,该模块里面有两个方法method1和method2.
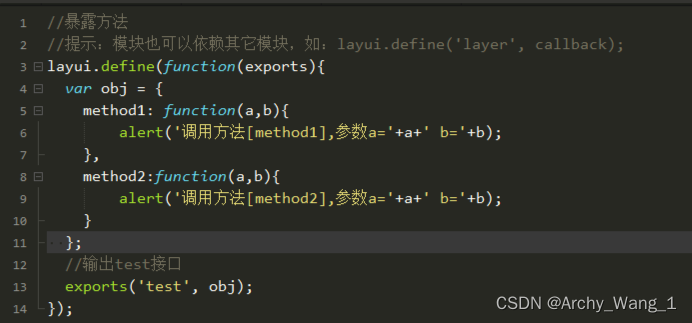
第三步:新建一个test.html,在该页面引入layui.js,并通过layui.config进行配置,用layui.use调用method1和method2两个方法。
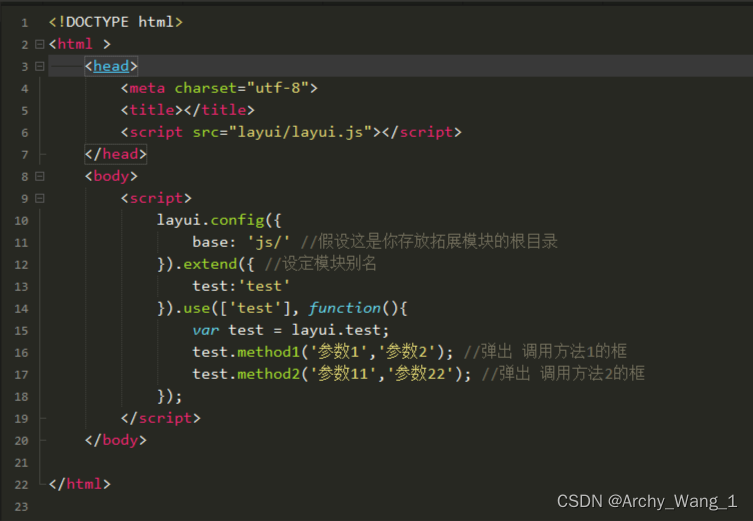
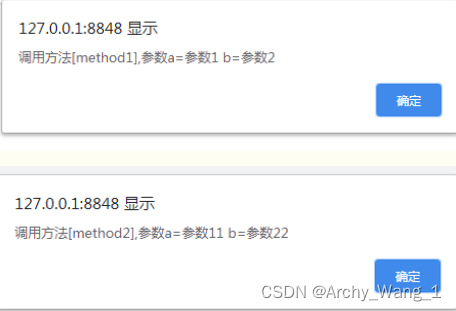
第四步:效果展示,在浏览器上打开页面地址,可以看到两次弹框。
相关文章:

layui项目中的layui.define、layui.config以及layui.use的使用
第一步:创建一个layuiTest项目,结构如下 第二步:新建一个test.js,利用layui.define定义一个模块test,并向外暴露该模块,该模块里面有两个方法method1和method2. 第三步:新建一个test.html,在该页面引入layui.js&#x…...

ChatGPT对话:Scratch编程中一个单词,如balloon,每个字母行为一致,如何优化编程
【编者按】balloon 7个字母具有相同的行为,根据ChatGPT提供的方法,优化了代码,方便代码维护与复用。初学者可以使用7个字母精灵,复制代码到不同精灵,也能完成这个功能,但不是优化方法,也没有提高…...

HTML【详解】超链接 a 标签的四大功能(页面跳转、页内滚动【锚点】、页面刷新、文件下载)
超链接 a 标签主要有以下功能: 跳转到其他页面 <a href"https://www.baidu.com/" target"_blank" >百度</a>href:目标页面的 url 地址或同网站的其他页面地址,如 detail.htmltarget:打开目标页面…...

Nginx+Tomcat群集
一.实验环境 二.安装多台Tomcat服务器 1.在安装Tomcat之前必须先安装JDK。 JDK的全称是Java Development Kit,是sun公司提供的JAVA语言的软件开发工具包,其中包含Java虚拟机(JVM),编写好的Java源程序经过编译可形成Ja…...

DBA 数据库管理 部署Mysql 服务,基础查询
数据库:存储数据的仓库 数据库服务软件: 关系型数据库: 存在硬盘 ,制作表格的 数据库的参数 [rootmysql50 ~]# cat /etc/my.cnf.d/mysql-server.cnf 主配置文件 [mysqld] datadir/var/lib/mysql 存放数据库目录…...

AIGC:构筑创意新时代的神奇力量
在当今数字化浪潮中,AIGC(人工智能生成内容)正以其强大的创造力和应用价值,引领着一场前所未有的创意革命。从文本生成到音乐创作,从图像设计到电影制作,AIGC的触角已延伸至文化艺术的各个领域,…...

前端Din字体和造字工房力黑字体文件
Din 字体是一种经典的、简洁的无衬线字体,它源自1930年代的德国交通标志设计。 造字工房力黑字体适用于数字,驾驶舱标题等统计界面 DIN-Medium.otf 案例 造字工房力黑.TTF 案例...

Studying-代码随想录训练营day33| 动态规划理论基础、509.斐波那契函数、70.爬楼梯、746.使用最小花费爬楼梯
第33天,动态规划开始,新的算法💪(ง •_•)ง,编程语言:C 目录 动态规划理论基础 动态规划的解题步骤 动态规划包含的问题 动态规划如何debug 509.斐波那契函数 70.爬楼梯 746.使用最小花费爬楼梯 总结 动态…...

【康复学习--LeetCode每日一题】724. 寻找数组的中心下标
题目: 给你一个整数数组 nums ,请计算数组的 中心下标 。 数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。 如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不…...

LeetCode-刷题记录-前缀和合集(本篇blog会持续更新哦~)
一、前缀和(Prefix Sum)算法概述 前缀和算法通过预先计算数组的累加和,可以在常数时间内回答多个区间和相关的查询问题,是解决子数组和问题中的重要工具。 它的基本思想是通过预先计算和存储数组的前缀和,可以在 O(1)…...

【中项第三版】系统集成项目管理工程师 | 第 4 章 信息系统架构③ | 4.6
前言 第4章对应的内容选择题和案例分析都会进行考查,这一章节属于技术相关的内容,学习要以教材为准。本章分值预计在4-5分。 目录 4.6 网络架构 4.6.1 基本原则 4.6.2 局域网架构 4.6.3 广域网架构 4.6.4 移动通信网架构 4.6.5 软件定义网络 4.6…...

知识图谱入门笔记
自学参考: 视频:斯坦福CS520 | 知识图谱 最全知识图谱综述 详解知识图谱的构建全流程 知识图谱构建(概念,工具,实例调研) 一、基本概念 知识图谱(Knowledge graph):由结…...

常见的气体流量计有哪些?
1.气体涡轮流量计 适用场合:流量变化小,脉动流频率小,中低压洁净天然气优点 1.精度高,重复性好 2.测量范围广,压损小,安装维修方便 3.具有较高的抗电磁干扰和抗震动能力缺点:分辨率低ÿ…...
:2024.07.01-2024.07.05)
AI推介-大语言模型LLMs论文速览(arXiv方向):2024.07.01-2024.07.05
文章目录~ 1.LLM Internal States Reveal Hallucination Risk Faced With a Query2.Fine-Tuning with Divergent Chains of Thought Boosts Reasoning Through Self-Correction in Language Models3.Investigating Decoder-only Large Language Models for Speech-t…...

Android IP地址、子网掩码、默认网关、首选DNS服务器、备用DNS服务器校验
Android IP地址、子网掩码、默认网关、首选DNS服务器、备用DNS服务器校验 public String isIP(String ip) {String regex = "(25[0-5]|2[0-4]\\d|1\\d{2}|[1-9]?\\d)(\\.(25[0-5]|2[0-4]\\d|1\\d{2}|[1-9]?\\d)){3}";Pattern p = Pattern.compile(regex)...

铁威马NAS教程丨为什么修复文件系统、为卷扩容、增加及删除 SSD 缓存等操作失败?
适用机型: 所有 TNAS 型号 适用版本: 所有 TOS 版本 问题现象: 在尝试修复文件系统、为卷扩容、增加或删除 SSD 缓存时(TOS 5),可能因卷被其他进程占用而操作失败。 解决方法: 为了成功执行上述操作,您…...

【深度学习】第3章——回归模型与求解分析
一、回归分析 1.定义 分析自变量与因变量之间定量的因果关系,根据已有的数据拟合出变量之间的关系。 2.回归和分类的区别和联系 3.线性模型 4.非线性模型 5.线性回归※ 面对回归问题,通常分三步解决 第一步:选定使用的model,…...

Maven的基本使用
引入依赖 1.引入Maven仓库存在的依赖,直接引入,刷新Maven <dependency><groupId>org.springframework</groupId><artifactId>spring-webmvc</artifactId><version>5.2.12.RELEASE</version> </dependency…...

【笔记】finalshell中使用nano编辑器GNU
ctrl O 保存 enter 确定 ctrl X 退出 nano编辑 能不用就不用吧 因为我真用不习惯 nano编辑的文件也可以用vim编辑的...

markdown文件转pdf
步骤:md转html转pdf pom引入 <!--markdown 转pdf--><dependency><groupId>com.vladsch.flexmark</groupId><artifactId>flexmark-all</artifactId><version>0.64.8</version></dependency><dependency&g…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...