05.C1W4.Machine Translation and Document Search
往期文章请点这里
目录
- Overview
- What you’ll be able to do!
- Learning Objectives
- Transforming word vectors
- Overview of Translation
- Transforming vectors
- Align word vectors
- Solving for R
- Frobenius norm
- Frobenius norm squared
- Gradient
- K nearest neighbors
- Finding the translation
- Nearest neighbours
- Hash tables and hash functions
- Hash tables
- Hash function
- Create a basic hash table
- Hash function v2
- Locality sensitive hashing
- Planes
- Which side of the plane?
- Visualizing a dot product
- Multiple Planes
- Approximate nearest neighbors
- Random Planes
- Multiple sets of random planes
- Searching documents
往期文章请点 这里
Overview
What you’ll be able to do!
machine translation,例如,英文→法文
document search,例如,根据给定句子:“Can I get a refund?”
搜索文档类似内容:
“What’s your return policy?”
“May I get my money back?”
Learning Objectives
“Transform vector”:转换向量
“K nearest neighbor”:K 最近邻
“Hash tables”:哈希表
“Divide vector space into regions”:将向量空间划分为区域
“Locality sensitive hashing”:局部敏感哈希
“Approximated nearest neighbors”:近似最近邻
Transforming word vectors
Overview of Translation
这里以英语翻译法语为例。

最笨的方法就是做一个英文与法文对应的列表。
如果要使用计算机来进行翻译,
先要将英文和法文的词向量表示给出来:

然后检索要翻译单词的词向量,如cat

将英文单词词向量转化为法文单词空间词向量:

在法语词向量空间中找到与转化结果最接近(相似)的词向量,最相似的单词就是翻译的候选单词,例如找到chat,就是法语中的cat

这里涉及到的Transform是用Matrix来完成的。
Transforming vectors
R = np. array([[2,0],[0,2]])
x = np. array([[1,1]])
np.dot(x,R)
最后结果:array([[2,2]]),从图像上看是这样的:

既然有向量 R R R使得英文词向量能转化为法文词向量,那我们来看看如何找到它。
Align word vectors
我们可以先随机初始化 R R R,然后查看转化的效果与实际法语词向量的差异。
首先要做的是对齐词向量,就是从词库中选择部分词(subsets of the full vocabulary),构造如下两个对齐向量:

每一行都是对应英法语的对应。
Solving for R
initialize R
in a loop:
L o s s = ∣ ∣ X R − Y ∣ ∣ F Loss=||XR-Y||_F Loss=∣∣XR−Y∣∣F
g = d d R L o s s g r a d i e n t g=\cfrac{d}{dR}Loss\quad gradient g=dRdLossgradient
R = R − α g u p d a t e R=R-\alpha g\quad update R=R−αgupdate
以上步骤中,损失函数求的是预测值 X R XR XR与实际值 Y Y Y之间的差异,我们希望差异越小越好,使用GD进行求解。
损失函数的下标F代表Frobenius范数,求法看下面
Frobenius norm
Frobenius范数是一种在矩阵理论中常用的范数,它定义为矩阵元素平方和的平方根。具体来说,对于一个 m × n m×n m×n的矩阵 A A A,其Frobenius范数表示为:
∥ A ∥ F = ∑ i = 1 m ∑ j = 1 n ∣ a i j ∣ 2 \| A \|_F = \sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} |a_{ij}|^2} ∥A∥F=i=1∑mj=1∑n∣aij∣2
robenius范数有时也被称为希尔伯特-施密特范数(Hilbert-Schmidt norm)
例子,假设我们只有2个单词,则矩阵有2行,词向量是2维的,则矩阵有2列, X R − Y XR-Y XR−Y的结果也是一个矩阵,记为 A A A,矩阵 X 、 R 、 Y X、R、Y X、R、Y和 A A A都是2乘2的矩阵,假设:
A = ( 2 2 2 2 ) A=\begin{pmatrix} 2 &2 \\ 2 & 2 \end{pmatrix} A=(2222)
∥ A ∥ F = 2 2 + 2 2 + 2 2 + 2 2 = 4 \| A \|_F =\sqrt{2^2+2^2+2^2+2^2}=4 ∥A∥F=22+22+22+22=4
A = np.array([[2,2],[2,2]])
A_squared = np.square(A)
A_squared
结果:array([[4,4],[4,4]])
A_Frobenious= np.sqrt(np.sum(A_squared))
A_Frobenious
结果:4
Frobenius norm squared
∣ ∣ X R − Y ∣ ∣ F 2 ||XR-Y||_F^2 ∣∣XR−Y∣∣F2
加上平方会让计算更加方便,去掉根号:
A = ( 2 2 2 2 ) A=\begin{pmatrix} 2 &2 \\ 2 & 2 \end{pmatrix} A=(2222)
∥ A ∥ F 2 = ( 2 2 + 2 2 + 2 2 + 2 2 ) 2 = 16 \| A \|_F^2 =(\sqrt{2^2+2^2+2^2+2^2})^2=16 ∥A∥F2=(22+22+22+22)2=16
Gradient
加上平方后,新的损失函数变成:
L o s s = ∣ ∣ X R − Y ∣ ∣ F 2 Loss=||XR-Y||_F^2 Loss=∣∣XR−Y∣∣F2
通过GD计算最小化Loss,变成求偏导操作:
g = d d R L o s s = 2 m ( X T ( X R − Y ) ) g=\cfrac{d}{dR}Loss=\cfrac{2}{m}(X^T(XR-Y)) g=dRdLoss=m2(XT(XR−Y))
K nearest neighbors
Finding the translation
在翻译英法语言过程中,我们通过R矩阵进行变换,得到的结果不一定与法语词向量空间中的单词完全对应:

这个时候需要我们找到最相近的词向量:

Nearest neighbours
先来看一个找朋友的例子,假设你住在三藩市,要找到最近的朋友:

Bangalore是印度的班加罗尔。
当你的朋友很多的时候,找到最邻近的朋友可能是一个非常耗时的过程。
可以考虑缩写查找范围,例如上例中我们可以将查找范围缩小到美国所在的北美洲过滤掉无关人员。
对于最邻近算法,可以设定一个搜索范围,有效提高算法效率。接下来我们将学习使用哈希表来组织数据集子集。
Hash tables and hash functions
Hash tables
假设有多个数据项,我们想通过某种相似性将它们分组到桶中

规则:
一个桶可有多个数据项
一个数据项属于某个桶
结果:

Hash function
其实这块在数据结构中有学过。
对于词向量而言,我们先从一维词向量来看,也就是单个数字,例如:
100 , 14 , 17 , 10 , 97 100,14,17,10,97 100,14,17,10,97
这里我们定义哈希函数来得到哈希值,并用哈希值来决定向量放入哪个桶中。

假设我们有10个桶,并将哈希函数定义为:

那么存放结果为:

Create a basic hash table
将以上内容编程实现:定义一个名为 basic_hash_table 的函数,用于创建一个基本的哈希表。这个哈希表使用一个列表来存储值,并使用一个简单的哈希函数来确定每个值应该存储在哈希表的哪个位置(即“桶”)。
def basic_hash_table(value_l, n_buckets):# 定义哈希函数,使用整数除法的余数来确定桶的位置def hash_function(value, n_buckets):return int(value) % n_buckets# 创建一个哈希表,其中包含n_buckets个空列表作为桶hash_table = {i: [] for i in range(n_buckets)}# 遍历输入值列表value_lfor value in value_l:# 对每个值使用哈希函数计算其哈希值hash_value = hash_function(value, n_buckets)# 将值添加到对应的桶中hash_table[hash_value].append(value)# 返回填充好的哈希表return hash_table# 使用示例:
# values = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# num_buckets = 3
# hash_table = basic_hash_table(values, num_buckets)
# print(hash_table)
注意:这段代码中的哈希函数非常简单,它只是取输入值的整数形式然后对桶的数量进行取模操作。这可能导致不同的输入值映射到同一个桶中,这种现象称为哈希冲突。在实际应用中,可能需要更复杂的哈希函数和冲突解决策略来提高哈希表的性能。
Hash function v2

之前的哈希函数并没有使得相近的数字在一个桶中,这样并不满足我们的计算邻近算法的要求,我们希望哈希表结果如下(Locality sensitive hashing):

Locality sensitive hashing
我们使用点来表示向量,并假设我们希望找到一种方法来使得蓝色、灰色向量是强相关的:

这里使用虚线来进行划分,但这些线称为Plane

可以看到,蓝色点在蓝色虚线的一侧,灰色点在灰色虚线的一侧。

也就是说这个划分方式是Locality sensitive的。
Planes

虽然在二维平面上,这里是一条紫色虚线,但是它实际上代表了所有可能位于该平面上的向量。例如下图中的橙色和蓝色向量

而紫色那个垂直于平面的,是法向量。
从三维空间上看,两个绿色向量组成一个平面,铅笔是法向量:

Which side of the plane?
在二维平面中如何判断向量和平面的位置呢?假设有三个示例向量和一个法向量P

分别求三个示例向量和法向量P的点积:
P V 1 T = 3 P V 2 T = 0 P V 3 T = − 3 PV_1^T=3\\ PV_2^T=0\\ PV_3^T=-3 PV1T=3PV2T=0PV3T=−3
总结来说,这三个示例向量与法向量 P 的点积结果表明它们与 P 之间的角度关系分别是锐角、直角和钝角。
第二示例向量是在平面内,而其他两个分别在平面上和下面。
def side_of_plane (P,v):dotproduct = np. dot (P,v.T)sign_of_dot_product = np.sign(dotproduct)sign_of_dot_product_scalar = np.asscalar(sign_of_dot_product)return sign_of_dot_product_scalar
Visualizing a dot product
查看 V 1 V_1 V1到向量P的投影,实际上是求 ∣ ∣ P V 1 T ∣ ∣ ||PV_1^T|| ∣∣PV1T∣∣

如果对另外一个向量进行投影,则会得到负值,这里的notation和前面不一样,要注意。

也就是说正负符号代表了向量相对法向量的位置,也决定了向量在平面的哪一侧。
Multiple Planes
由于正负号决定了向量所处平面的位置,因此可以用多个平面来确定某个哈希值。

从上图可知,通过每个区域的不同信号,可以确定当前向量所处的位置。划分这些区域的过程就是哈希函数,通过哈希函数可以确定哈希值。
例如对于三个平面,某向量对它们的相对位置可以用以下方式计算,注意框框颜色与平面颜色对应:

该向量的hash值为:
h a s h = 2 0 × h 1 + 2 1 × h 2 + 2 2 × h 3 = 1 × 1 + 2 × 1 + 4 × 0 = 3 hash=2^0\times h_1+2^1\times h_2+2^2\times h_3=1\times1+2\times1+4\times0=3 hash=20×h1+21×h2+22×h3=1×1+2×1+4×0=3
通用的判定写法为:
s i g n i ≥ 0 , → h i = 1 s i g n i < 0 , → h i = 0 sign_i\ge 0,\rightarrow h_i=1\\ sign_i< 0,\rightarrow h_i=0 signi≥0,→hi=1signi<0,→hi=0
最终hash值公式:
h a s h = ∑ i H 2 i × h i hash = \sum_i^H2^i\times h_i hash=i∑H2i×hi
代码:
def hash_multiple_plane (P_l,v)hash_value = 0for i, P in enumerate (P_l):sign = side_of_plane(P,v)hash_i = 1 if sign >= 0 else 0hash_value+=2**i*hash_ireturn hash_value
Approximate nearest neighbors
Random Planes
在近似最近邻(Approximate Nearest Neighbors,简称ANN)的搜索算法中,“Random Planes” 通常指的是一种基于随机划分空间的方法,用于加速搜索过程。这种方法在一些ANN算法中被用来减少搜索空间,例如在局部敏感哈希(Locality-Sensitive Hashing,LSH)算法中。
在Random Planes方法中,随机平面的组数取决于具体的算法实现和参数设置。在某些实现中,可能只使用一组随机平面来划分空间,而在其他更复杂的实现中,可能会使用多组随机平面。使用多组随机平面可以提高搜索的准确性,因为它们可以从不同的角度对空间进行划分,从而增加找到真正最近邻的可能性。

可将不同组的Random Planes看做是不同的平行宇宙。
Multiple sets of random planes
假设我们将英法翻译得到词向量用紫色表示,然后使用了三组不同的随机平面进行划分,得到最紫色向量最邻近的结果也有三组,分别用三种颜色表示。

可以看到,不同组的平面划分得到结果也不一样,这种划分方法在紫色向量找朋友的时候没有与所有的其他向量进行比较,只比较了子集,因此只能称为:Approximate nearest (friendly) neighbors算法
假设词向量有2个维度,要生成三个随机平面:
num_dimensions = 2 #300 in assignment
num_planes = 3 #10 in assignment
random_planes_matrix = np. random.normal(size=(num_planes,num_dimensions))
结果:
array([[ 1.76405235 0.40015721]
[ 0.97873798 2.2408932 ]
[ 1.86755799 0.97727788]])
然后判断向量处于平面集合的哪个位置:
v = np. array([[ 2,2]])
然后判断向量位置:
def side_of_plane_matrix (P, v):dotproduct = np. dot (P, v.T)sign_of_dot_product=np.sign(dotproduct)
num_planes_matrix = side_of_plane_matrix(random_planes_matrix,v)
结果
array([[1.]
[1.]
[1.])
Searching documents
对应文档有以下句子:
I love learning!
其对应的文档向量表示可以从各个单词的sum得来

word_embedding = {"I": np.array([1,0,1]),
"love": np.array([-1,0,1]),
"learning": np.array([1,0,1]),words_in_document = ['I', 'love', 'learning']
document_embedding= np. array ([0 0 0])
for word ind words_in_document:document_embedding+=
print(document_embedding)
相关文章:

05.C1W4.Machine Translation and Document Search
往期文章请点这里 目录 OverviewWhat you’ll be able to do!Learning Objectives Transforming word vectorsOverview of TranslationTransforming vectors Align word vectorsSolving for RFrobenius normFrobenius norm squaredGradient K nearest neighborsFinding the tr…...
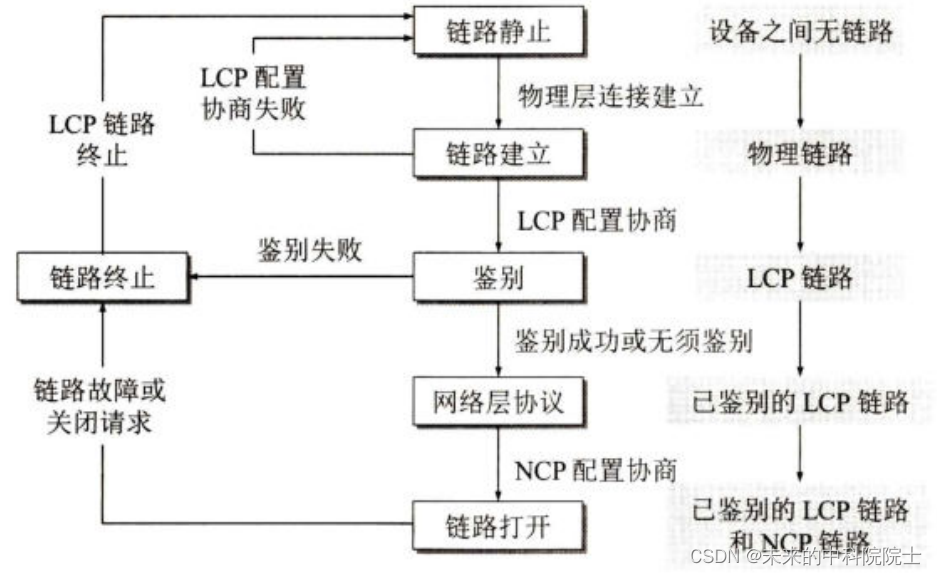
计算机网络——数据链路层(点对点协议PPP)
点对点协议PPP的概述 对于点对点的链路,目前使用得最广泛的数据链路层协议是点对点协议 PPP (Point-to-Point Protocol)。 它主要应用于两个场景: 用户计算机与ISP之间的链路层协议就是点对点协议 PPP,1999年公布了回以在以太网上运行的PPP协…...

信息安全概述
名词解释 大数据:指的是所涉及的资料量规模巨大到无法透过主流软件工具,在合理时间内达到撷取、管理、处理、并整理成为帮助企业经营决策更积极目的的资讯。 云计算:是指通过网络提供计算资源(如服务器、存储、数据库、软件开发…...

UE5.3-基础蓝图类整理一
常用蓝图类整理: 1、获取当前关卡名:Get Current LevelName 2、通过关卡名打开关卡:Open Level(by name) 3、碰撞检测事件:Event ActorBeginOverlap 4、获取当前player:Get Player Pawn 5、判断是否相等࿱…...

Python面试题: 如何在 Python 中实现一个线程池?
在 Python 中,实现线程池可以使用内置的 concurrent.futures 模块,该模块提供了一个高层次的接口来管理并发任务。ThreadPoolExecutor 类是实现线程池的主要工具。以下是一些使用示例,展示如何在 Python 中实现和使用线程池: 1. …...

☺初识c++(语法篇)☺
目录 一命名空间(namespace): 二cout与cin简述: 三缺省参数: 四函数重载: 五引用: 六内联函数: 七c中的nullptr简述: 一命名空间(namespace)࿱…...

process.env 管理 Vue 项目的环境变量(Vue项目中环境变量的配置及调用)
简述:在构建 Vue 应用时,管理配置是开发中的一个重要部分。不同的环境(如开发、测试和生产)往往需要不同的配置,例如 API、 基础 URL、第三方服务的密钥等。使用环境变量可以帮助我们更好地管理这些配置。这里将介绍如…...
)
算法工程师第六天(● 454.四数相加II ● 383. 赎金信 ● 15. 三数之和 ● 18. 四数之和 ● 总结 )
参考文献 代码随想录 一、四数相加 II 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1[i] nums2[j] nums3[k] nums4[l] 0 示例 1&#…...

笔记:Newtonsoft.Json 自定义一个根据typeconverter转换的JsonConverter
在 Newtonsoft.Json 中创建一个根据 TypeConverter 转换的 JsonConverter 允许你在序列化和反序列化过程中利用 .NET 的 TypeConverter 机制。这种方式特别有用,当你想要为不直接支持 JSON 序列化的类型提供自定义的序列化逻辑时,比如第三方库中的类型或…...

第241题| 确定极限中参数问题 | 武忠祥老师每日一题
解题思路:确定极限中的参数的方法是求这个极限;求极限根据类型选方法。 形可以用到三种方法:洛必达,等价,泰勒。 先观察题目,将看成一个整体,同时,并令,整理之后如下: 这里也要想办…...

线程池【开发实践】
文章目录 一、为什么要用线程池1.1 单线程的问题1.2 手动创建多线程的问题1.3 线程池的作用(优点)1.4 线程池的使用场景 二、线程池的基础知识2.1 线程池的核心组件2.2 JUC中的线程池架构2.3 线程池的配置参数2.4 线程池常见的拒绝策略(可自定…...

论文辅助笔记:ST-LLM
1 时间嵌入 2 PFA(Partial Frozen Architecture) 3 ST_LLM 3.1 初始化 3.2 forward...

加入运动健康数据开放平台,共赢鸿蒙未来
HarmonyOS SDK运动健康服务(Health Service Kit)是为华为生态应用打造的基于华为帐号和用户授权的运动健康数据开放平台。在获取用户授权后,开发者可以使用运动健康服务提供的开放能力获取运动健康数据,基于多种类型数据构建运动健…...
企业化运维(7)_Zabbix企业级监控平台
官网:Zabbix :: The Enterprise-Class Open Source Network Monitoring Solution ###1.Zabbix部署### (1)zabbix安装 安装源 修改安装路径为清华镜像 [rootserver1 zabbix]# cd /etc/yum.repos.d/ [rootserver1 yum.repos.d]# vim zabbix.r…...

CTF php RCE (一)
0x01 引言 首先进入题目 应该是大部分都是一段白盒PHP审计,然后我们为了命令执行,绕过或者是钻空子等等操作,来拿到flag 0x02 基础 0x01 传参方式 这里有两个工具,hackbar和burpsuite,这两个工具非常实用 大家可以自己Googl…...

Proteus + Keil单片机仿真教程(五)多位LED数码管的静态显示
Proteus + Keil单片机仿真教程(五)多位LED数码管 上一章节讲解了单个数码管的静态和动态显示,这一章节将对多个数码管的静态显示进行学习,本章节主要难点: 1.锁存器的理解和使用; 2.多个数码管的接线封装方式; 3.Proteus 快速接头的使用。 第一个多位数码管示例 元件…...

【Linux】网络新兵连
欢迎来到 破晓的历程的 博客 ⛺️不负时光,不负己✈️ 引言 在上一篇博客中,我们简单的介绍了一些Linux网络一些比较基本的概念。本篇博客我们将开始正式学习Linux网络套接字的内容,那么我们开始吧! 1.网络中的地址管理 大家一…...

基于STM32的智能加湿器
1.简介 基于STM32的加湿器发展前景非常乐观,这主要得益于其在技术、市场需求、应用场景以及政策支持等多方面的优势。STM32微控制器具备强大的处理能力和丰富的外设接口,能够实现精确的湿度监测和智能化控制。基于STM32的加湿器可以根据环境湿度自动调节…...

ubuntu 如何解压tar
在Ubuntu中解压.tar文件,可以使用tar命令。以下是解压.tar文件的命令: tar -xvf file.tar 解释: x 表示解压 v 表示显示过程中的详细信息(可选) f 表示后面跟文件名 这将在当前目录下解压file.tar文件的内容。如果…...

C++ 算法——二分查找
如果要你在一个升序序列中查找一个值的位置,你是否还会傻乎乎的用下面这个 O ( n ) \mathcal O(n) O(n) 的代码暴力查找,如果是,我告诉你,其实根本不用这么做。 int find(int a[],int n,int k) {for(int i0;i<n;i) if(a[i]k)…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
