一分钟理解 AP(Affinity Propagation) 亲和⼒传播算法
从来没有一个算法让我研究好几天都搞不明白,AP算法算是第一个。弄了好几天,打草纸用了几十页,反复琢磨,最后都怀疑人生了。我觉得网上那么多介绍 AP 的文章,基本上没有一篇能讲明白的。最后我都觉得 AP 的作者可能都没弄明白。
看在这篇论文发表在美国科学杂志的份上,终于耐着性子,梳理出其中的思路。在此奉献给大家,如果我这篇文章你都看不懂,那就洗洗睡吧,别伤脑筋了。
1. 基本思路
AP 算法的灵感来自投票选举。我们看下面的故事:
1.1 划分部落,选举首领
辽阔的草原上居住一群人。为便于组织管理,他们想通过投票选举部落首领,把人群分成若干部落,每个部落有一个首领。
投票规则很简单,(1) 每个人只能推选一个人做自己的首领; (2) 想当部落首领的人必须投票给自己。
AP 算法的基本思路是,开始的时候每个人的自我支持度设置为较低的数值,然后整个选举过程不断提升潜在首领的自我支持度和其他人对潜在首领的支持度,同时降低对民意较差的候选人的支持度。整个过程关注两件事情:
- 如何发现潜在的部落首领?
- 如何让选民加入正确的部落?
1.2 按亲情投票
其实人性决定了投票的倾向性,大家都愿意投给最亲近的人。可是谁是自己最亲近的人呢?很显然自己与自己是最亲近的。但是,如果每个人都投票给自己,按照规则就只能一个人组成一个部落。大家都明白这一点,于是人们虚伪宣布自己绝不亲近自己,如果世界上只有一个仇人,那就是我自己。
接下来,我用投票支持度这个词来说明选民对候选人的支持程度或者亲密程度。人群中的每一个人在选举中,既是选民,又是候选人。
第一轮投票的结果是,大家把票都投给了其他与自己最亲近的人,比如自己的老公,自己的儿子等。因为第一轮投票所有人都不会推选自己,所以投票后必然无法完成划分部落的任务。
1.3 发现潜在的部落首领
但是,第一轮投票还是有成果的。大家统计了一下票数,发现有些人得了一些票,未来有可能被推选为某个部落首领,还有些人没有得到投票,成为首领的可能性就低一些。
要利用这次的投票结果完成两件事情:
-
第一件事情,根据当前投票结果,每个人都要想法提升对自己的支持度,以便能产生部落首领。方法很简单,只要把其他人对自己的支持度累加起来,叠加到自我支持度上即可。
-
第二件事情,根据当前投票结果,每个人都要想法降低对其他人的支持度,以便淘汰无希望的候选者。方法也很简单,比如张三想降低对李四的支持度,他就先看一下李四的自我支持度以及群众(张三和李四以外的其他人)的支持度,如果这个支持度很高,张三就不降低对李四的支持度。如果这个支持度不是很高,就酌情降低对李四的支持度。
这样一来的话,有些人的自信心越来越足,越来越愿意把票投给自己。有些人的自信心越来越低,越来越越愿意投票给其他人。
1.4 投票方法的可收敛性
最后还剩一个问题,为什么自信心较低的这些人愿意把票投给潜在的部落首领呢?
这个问题的原因也很简单。例如张三决定降低对李四的支持度的时候,如果李四的自我支持度很高,可能导致张三不会降低、或者略微降低对李四的支持度,从而导致张三对李四的支持度较高一些。反之,如果李四自我支持度较低,其他人对他支持度也不高,就会导致张三会大幅度降低对李四的支持度。也就是说,张三对李四支持度的变化,是受其他人影响的,因此,最终产生”从众“效应,从而能够形成统一意见,选出部落首领。
2. 一个简单例子
为简化问题,我们提供一个极为简单的例子,假设点分布在实数轴上,坐标分别为 :
A=1,B=2,C=3,D=5,E=6A=1,B=2,C=3,D=5,E=6 A=1,B=2,C=3,D=5,E=6
2.1 相似度矩阵 s
用两个点之间的距离的负数作为两个点之间相似度,也就是所谓的亲和力。两个点之间的相似度越大,说明两个点属于一个类别的可能性越大。根据上述坐标,可以得出相似度矩阵:
| i \ k | A | B | C | D | E |
|---|---|---|---|---|---|
| A | - | -1 | -2 | -4 | -5 |
| B | -1 | - | -1 | -3 | -4 |
| C | -2 | -1 | - | -2 | -3 |
| D | -4 | -3 | -2 | - | -1 |
| E | -5 | -4 | -3 | -1 | - |
按照距离的负数计算相似度,导致相似度全部都是负数。不过没关系,只要能保证数值越大,相似度越高即可,至于数据的符号,初始阶段并不重要。
对角线 s(i,i)s(i,i)s(i,i) 表示自己与自己的亲和力,按理说应该取 000 或上述矩阵中最大的值。但实际上不能这么干,如果每个人都认为自己最适合当领导的话,就无法聚类了。因此,AP算法建议选择上述矩阵中元素的最小值或者中位数。接下来我们选择最小值得到完整的相似度矩阵:
| i \ k | A | B | C | D | E |
|---|---|---|---|---|---|
| A | -5 | -1 | -2 | -4 | -5 |
| B | -1 | -5 | -1 | -3 | -4 |
| C | -2 | -1 | -5 | -2 | -3 |
| D | -4 | -3 | -2 | -5 | -1 |
| E | -5 | -4 | -3 | -1 | -5 |
一般来讲,AP算法的灵感来自一个群体通过自发投票选举小组领导人的过程。人们投票一般取决于两个策略:任人唯亲、兼顾民意。比如,你想推选自己的儿子做村长,但是考虑到自己的儿子实在不受大家喜欢,于是投票给了人缘稍微好一点的侄子。这样做不至于把选票浪费在毫无希望的儿子身上,同时又耽误了有希望竞选成功的侄子。
相似度矩阵可以这样理解,行 iii 代表选民,列 kkk 代表竞选人。因为 s(i,i)s(i,i)s(i,i) 选择了矩阵元素的最小值,这表示开始阶段,每个人都不希望自己被选举为领导人。接下来的过程,我们要说服某些优势候选人提升自己成为领导人的意愿,同时也要说服选民选择把票投给具备民意基础的优势候选人。
2.2 亲情矩阵 r
上面的相似度矩阵虽然在一定程度上反映了亲情关系,但是,不同行之间数据是不能进行比较的。例如,第1行第2列最大值是-1,意味着选民1会投票给2。但是第2行的最大值-1有两个,意味着选民2会投票给选民1和3。第2行的两个-1才相当于第一行的一个-1。因此,我们需要把相似度矩阵 sss 归一化,得到一个标准化的"亲情矩阵"。
用下面的公式生成亲情矩阵 rrr:
r(i,k)=s(i,k)−maxk′≠k{s(i,k′)+a(i,k′)}(1)\tag1 r(i,k)=s(i,k)-\max_{k' \neq k}\{s(i,k')+a(i,k')\} r(i,k)=s(i,k)−k′=kmax{s(i,k′)+a(i,k′)}(1)
其中 a(i,k′)a(i,k')a(i,k′) 在初始阶段为零矩阵,其具体含义后面会解释。因此,矩阵 r(i,k)r(i,k)r(i,k) 结果如下:
| i \ k | A | B | C | D | E |
|---|---|---|---|---|---|
| A | -4 | 1 | -1 | -3 | -4 |
| B | 0 | -4 | 0 | -2 | -4 |
| C | -2 | 1 | -4 | -2 | -3 |
| D | -3 | -2 | -1 | -4 | 1 |
| E | -4 | -3 | -2 | 2 | -4 |
这个矩阵反映了在选民 iii 对候选人 kkk 的支持度。一般来讲,每个选民只能投票给一个候选人,大都数情况下,矩阵的每一行只有一个正向支持度,其余的为负向支持度。
如果我们认为正向支持度表示支持,零支持度表示不反对不支持,负支持度表示反对,那么,当前的情况表明:A、C支持B,但 B 反对自己;同时呢,D、E都支持对方,同时都反对自己。因此,目前是无法实现聚类的。
聚类成功的条件应该是,聚类中心首先自己要支持自己,然后其他候选人都应该支持某个聚类中心。
接下来要解决两个问题:
- 【问题1】如何让 B 支持自己
- 【问题2】如何说服 D、E中的一个支持对方,而另一个能支持自己。
解决方法是通过民意调查,改变选民的对候选人的支持度。
2.3 民意矩阵 a
接下来,大家根据当前 rrr 提供的支持度结果,做进一步的决策调整。简单地讲,基本策略就是”批评与自我表扬“。虽然一开始大家都很谦虚,自我支持度设置成为一个较低的起点。但是,竞选已经开始了,每个人都需要找理由加强自我支持度,降低对其他人的支持度。所以后续步骤就是找理由增加对自己的支持度,降低对别人的支持度。
2.3.1 表扬自我
我们可以把候选人 kkk 对自己的支持度理解为候选人的自信心。初始阶段,自我支持度 r(k,k)r(k,k)r(k,k) 都是负值,呈现出完全没有自信心的样子。我们需要根据选民的投票意向,提升候选人的自信心。计算方法是,把矩阵 rrr 每一列中的正数累加起来保存在对角线 a(k,k)a(k,k)a(k,k) 的位置。公式如下:
a(k,k)=∑i′≠kmax{(0,r(i′,k))}(2)\tag2 a(k,k)=\sum_{i'\neq k}\max\{(0,r(i',k))\} a(k,k)=i′=k∑max{(0,r(i′,k))}(2)
这样我们得到了民意矩阵主对角线的值:
| i \ k | A | B | C | D | E |
|---|---|---|---|---|---|
| A | 0 | 0 | 0 | 0 | 0 |
| B | 0 | 2 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | 2 | 0 |
| E | 0 | 0 | 0 | 0 | 1 |
显然,候选人 B、D、E 找到了提升自我支持度的理由。
2.3.2 批评别人
接下来要找理由降低对其他人的支持度。当然这个理由应该优雅一些。主要原则如下:
- 既然是降低对别人的支持度,这个增量必然不会是大于零的数值。
- 也不能太过分,降低幅度尽量不要太多。
选民 iii 对候选者 kkk 的支持度,会受其他选民支持度的影响。其影响程度包括两部分:
- 候选者 kkk 自信心 r(k,k)r(k,k)r(k,k) 。候选者自信心很重要,后面我们会看到,候选人 kkk 自我支持度大于对其他人的支持度,也就是自己愿意投票给自己时,他才能成为聚类中心。
- 其他选民 i′i'i′ 对候选者 kkk 的正的投票意向 ∑i′∉{i,k}{max(0,r(i′,k))}\sum_{i' \notin \{i,k\}} \{\max(0,r(i',k))\}∑i′∈/{i,k}{max(0,r(i′,k))}
也就是说,如果 kkk 自己有信心,其他选民也都支持 kkk 。显然:
- 如果二者之和大于零,也就是民意非常正面,iii 就没有理由降低对 kkk 的支持度。
- 如果二者之和小于零,也就是民意非常负面,iii 就可以用这个结果作为对 kkk 支持度的增量。因为计算过程中采用 max\maxmax 运算,可以说 iii 对 kkk 还是手下留情了,选择了较小幅度的负增量。
综上述,民意矩阵计算公式如下:
【表扬自我】:
a(k,k)=∑i′≠kmax{(0,r(i′,k))}(3)\tag3 a(k,k)=\sum_{i'\neq k}\max\{(0,r(i',k))\} a(k,k)=i′=k∑max{(0,r(i′,k))}(3)
【批评别人】:
a(i,k)=min{0,r(k,k)+∑i′∉{i,k}{max(0,r(i′,k))}},i≠k(4)\tag4 a(i,k)=\min\{0,r(k,k)+\sum_{i' \notin \{i,k\}} \{\max(0,r(i',k))\}\},i \neq k a(i,k)=min{0,r(k,k)+i′∈/{i,k}∑{max(0,r(i′,k))}},i=k(4)
把亲情矩阵 r(i,k)r(i,k)r(i,k) 复制下来:
| i \ k | A | B | C | D | E |
|---|---|---|---|---|---|
| A | -4 | 1 | -1 | -3 | -4 |
| B | 0 | -4 | 0 | -2 | -4 |
| C | -2 | 1 | -4 | -2 | -3 |
| D | -3 | -2 | -1 | -4 | 1 |
| E | -4 | -3 | -2 | 2 | -4 |
按照上述公式,民意矩阵 a(i,k)a(i,k)a(i,k) 计算结果如下:
| i \ k | A | B | C | D | E |
|---|---|---|---|---|---|
| A | 0 | -3 | -4 | -2 | -3 |
| B | -4 | 2 | -4 | -2 | -3 |
| C | -4 | -3 | 0 | -2 | -3 |
| D | -4 | -2 | -4 | 2 | -4 |
| E | -4 | -2 | -4 | -4 | 1 |
发现一个很有意思的现象,由于候选人 A 没有获得正向支持度,他的民意支持度就是自己的自信心 −4-4−4,所以 A 这一列很惨哦。同样候选人 C 这一列也很惨烈!
这个增量矩阵 aaa 对角线以外的其它元素基本上都是小于零的,勇于“批评与自我表扬”的特点表现得淋漓尽致呀!
- 候选人 B 通过 a(2,2)a(2,2)a(2,2) 的计算,可以把 r(2,2)=−4r(2,2)=-4r(2,2)=−4 提升至 c(2,2)=r(2,2)+a(2,2)=−2c(2,2)=r(2,2)+a(2,2)=-2c(2,2)=r(2,2)+a(2,2)=−2。
- 候选人的其他列 a(2,k),k≠2a(2,k),k\neq 2a(2,k),k=2 都小于等于零,因此,B 对他们的支持度会下降,下降幅度取决于这些列的候选人的民意支持度。如果其他人对这些列支持度较高,B对他们支持下降的幅度就会降低,否则,下降幅度就会加大。但无论如何,B 不会提升对他们的支持都。
矩阵 aaa 还有一个很有趣的现象,每行元素,例如第一、二、三行,选民 A、B、C 除了最支持自己外,其次就是很支持 D。再看矩阵 aaa 的第四、五行,选民 D、E 除了支持自己外,其次就是很支持 B。这导致后面 B 和 D 脱颖而出。
2.4 决策矩阵 c
决策矩阵用来决定是否结束算法。决策矩阵 c(i,k)c(i,k)c(i,k) 计算方法如下:
c(i,k)=r(i,k)+a(i,k)(5)\tag5 c(i,k)=r(i,k)+a(i,k) c(i,k)=r(i,k)+a(i,k)(5)
即综合考虑亲情和民意。根据上述数据,c(i,k)c(i,k)c(i,k) 计算结果如下:
| i \ k | A | B | C | D | E |
|---|---|---|---|---|---|
| A | -8 | -2 | -5 | -5 | -7 |
| B | -4 | [-2] | -4 | -4 | -7 |
| C | -6 | -2 | -4 | -4 | -6 |
| D | -7 | -4 | -5 | [-2] | -3 |
| E | -8 | -4 | -6 | -2 | -3 |
决策过程如下:
- 首先把每一行的最大值标出来(黑体字),如果最大的元素在对角线上,该元素就是聚类中心。
- 然后检查矩阵每一个行,看看是否都投票给了聚类中心,即该行的最大值都落在某个聚类中心那一列上,本例是B、D这两列。如果有些选民没有投票给聚类中心,接下来要回到步骤 “3.亲情矩阵r(i,k)”,继续迭代。
本例可以看出聚类中心是 B 和 D,两个聚类子集分别是:
SB={A,B,C}SD={D,E}S_B=\{A,B,C\}\\ S_D=\{D,E\} SB={A,B,C}SD={D,E}
3. 问题和质疑
先回答一下文章开头提的问题。
-
如何发现潜在的部落首领?
答:亲情 + 民意。 -
如何让选民加入正确的部落?
答:亲情 + 民意。
写到这里,我已经精疲力尽了。还有些问题,等下一篇博文再仔细讨论。
【问题1】如果第一轮投票未能完成聚类,接下来的迭代为什么要用 sss 和 s+as+as+a 进行计算? 参见公式(1)。为什么不用决策矩阵 ccc 来计算下一轮的 rrr?
这个算法的机理的确复杂,我的解释也未必完美。大家有什么质疑请留言,希望能够通过讨论把这个问题彻底整明白。
相关文章:
 亲和⼒传播算法)
一分钟理解 AP(Affinity Propagation) 亲和⼒传播算法
从来没有一个算法让我研究好几天都搞不明白,AP算法算是第一个。弄了好几天,打草纸用了几十页,反复琢磨,最后都怀疑人生了。我觉得网上那么多介绍 AP 的文章,基本上没有一篇能讲明白的。最后我都觉得 AP 的作者可能都没…...

使用mybatis的映射文件操作存储过程
先随便创建一个存储过程 DELIMITER $$ CREATE PROCEDURE getUserNameById (IN i_id BIGINT, OUT o_name VARCHAR(10)) BEGINSELECT u.name INTO o_name FROM tb_user u WHERE id i_id; END $$delimiter $$ : 是将sql语句的结束符号先替换成$$的意思,因为sql是遇到…...

世界上最完美的两个软件,太厉害了!
今天给大家介绍两个软件,一个体现了人类在软件开发流程上的极致,另外一个则体现了程序员个体能力的巅峰。01航天飞机飞控软件先来说第一个,航天飞机飞行控制软件,就是下图这个大家伙。航天飞机重达120吨,还携带着2000吨…...
教你成为比卡卡西还牛逼的全能忍者,全拷贝与分割函数
如何成为一个集雷切,写轮眼侦查和拷贝与一身的卡卡西,下面教你! 目录 第一式——雷切! strtok 第二式——写轮眼侦查! strerror函数 第三式——写轮眼拷贝! memcpy 模拟实现memcpy函数 😎…...

【LeetCode】剑指 Offer(24)
目录 题目:剑指 Offer 47. 礼物的最大价值 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer 47. 礼物的…...

javaEE 初阶 — CSS 元素的显示模式与盒模型
文章目录1. 元素的显示模式1.1 块级元素1.2 行内元素1.3 行内元素和块级元素的区别1.4 改变显示模式2. 盒模型2.1 边框2.1.1 边框的粗细2.1.2 边框的颜色2.1.3 边框的风格2.2 内边距2.3 外边距2.3.1 margin 的特殊情况1. 元素的显示模式 1.1 块级元素 常见的元素: h1 - h6 、…...

新星计划-我为什么要写博客?写博客的意义是什么
CSDN的各位友友们你们好,今天千泽要和大家交流一下写博客的意义,并且鼓励大家参加CSDN官方举办的新星计划,这个可以让我们更快的成长,十分有价值.接下来让我们一起开始吧!如果对您有帮助的话希望能够得到您的支持和帮助,我会持续更新的!🚩part1:自我介绍我是一名来自…...
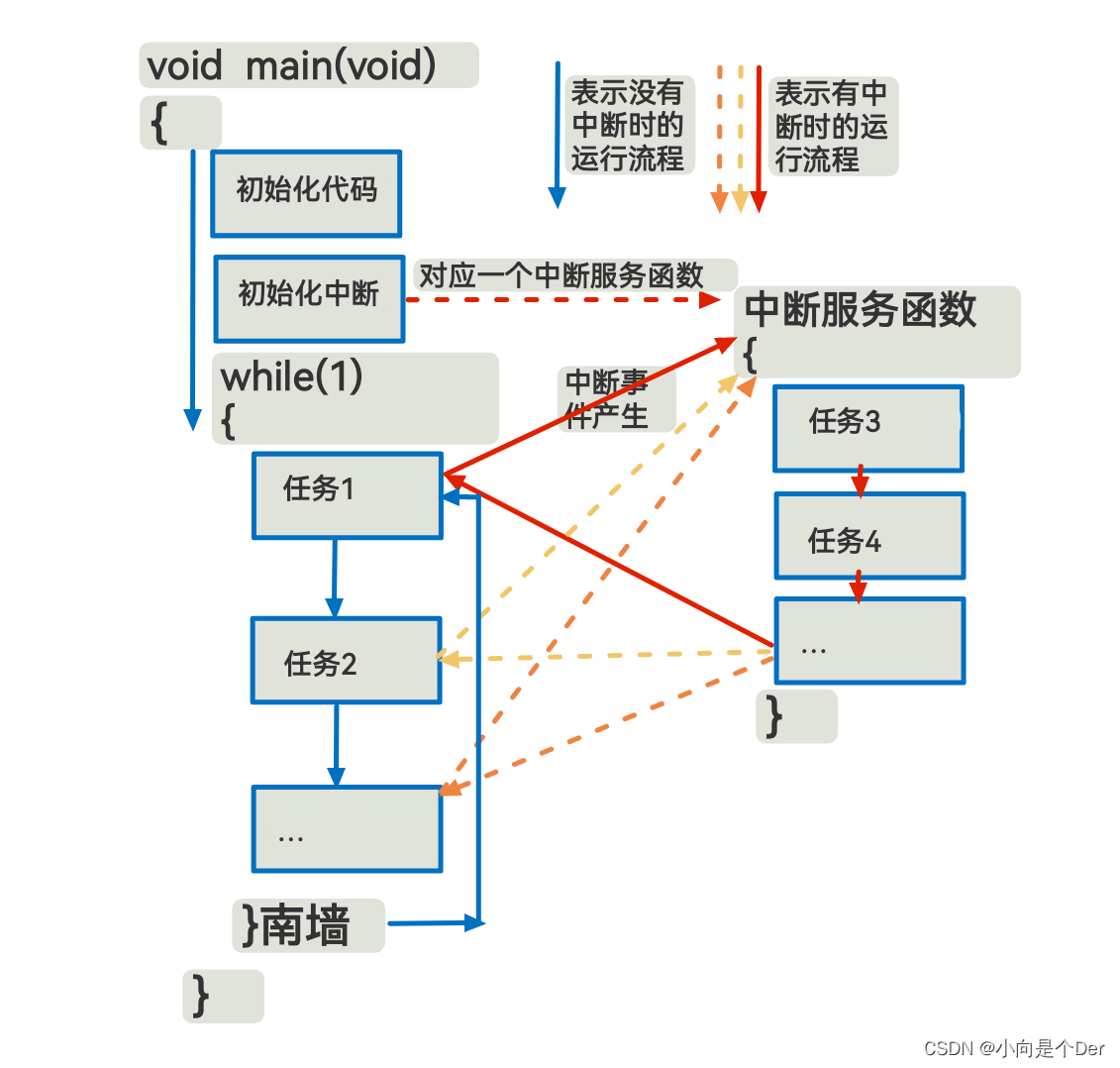
嵌入式学习笔记——STM32的USART收发字符串及串口中断
USART收发字符串及串口中断前言字符串的收发发送一个字符串接收字符串需求利用串口实现printf中断中断是什么前言 上一篇中,介绍了串口收发相关的寄存器,通过代码实现了一个字节的收发,本文接着上面的内容,通过功能函数实现字符串…...
)
数据分析之Pandas(1)
3.Pandas 文章目录3.Pandas3.1 Pandas基本介绍3.1.1 Pandas的基本数据结构3.1.1.1 Pandas库的Series类型3.1.1.2 Pandas库的DataFrame类型DataFrame初始化DataFrame查看数据3.1.2 Pandas读取数据及数据操作行操作添加一行删除一行列操作增加一列删除一列通过标签选择数据条件选…...
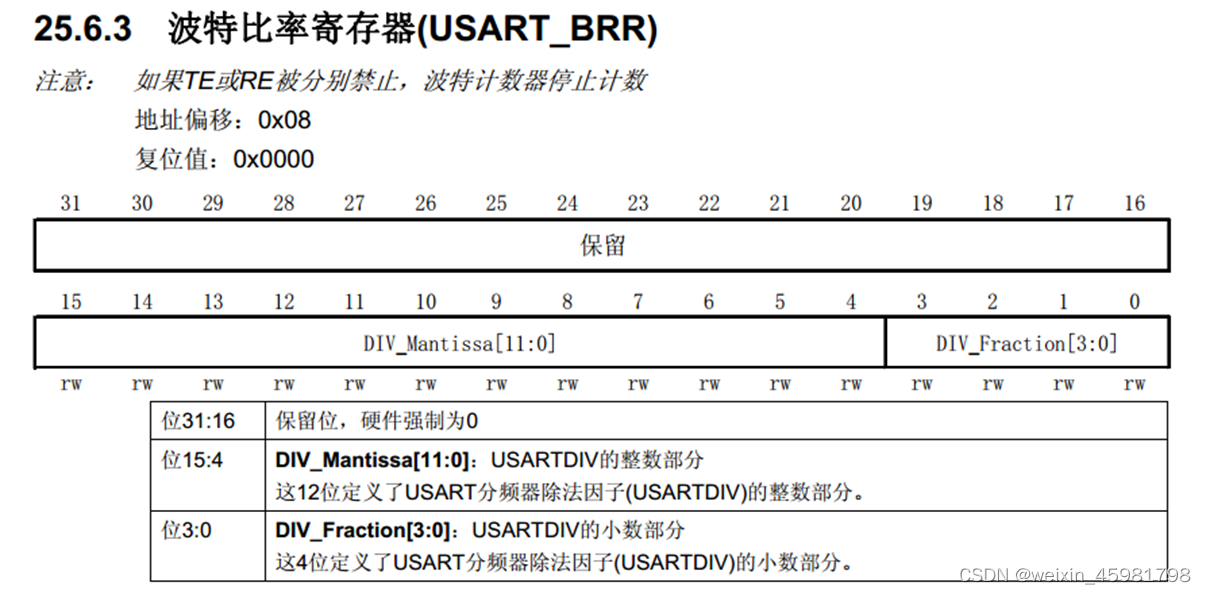
17、江科大stm32视频学习笔记——USART串口协议和USART串口外设
目录 1、通信接口 2、 硬件电路 3、电平标准 4、串口参数及时序 5、USART简介 6、USART工作 (1)写操作 (2)读操作 (3)帧头和帧尾的添加和除由电路自动执行 (4)硬件数据控制…...

leetcode:有效地括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右括号都…...

四等分list
Testpublic void s (){ int targ 4; List mList new ArrayList(); List<List> mEndList new ArrayList<>(); for (int i 0; i <34; i) { mList.add(“item” i); } // System.out.println(mList.toString()); if (mList.size() % targ ! 0) { for (int j …...

php连接sqlserver数据库
docker 安装sqlserver数据库sudo docker pull mcr.microsoft.com/mssql/server:2017-latestsudo docker run -e "ACCEPT_EULAY" -e "MSSQL_SA_PASSWORD<YourStrongPassw0rd>" -p 1433:1433 --name sqlserver --hostname sqlserver -d mcr.microsoft.…...

The 2019 China Collegiate Programming Contest Harbin Site F. Fixing Banners
Problem - F - Codeforces 翻译: 哈尔滨,这个名字最初是一个满语单词,意思是“晒渔网的地方”,从松花江边的一个小农村居民点发展成为中国东北最大的城市之一。1898年,随着中国东部铁路的到来,这座城市首先…...
Maven的下载和配置
一、前言 一般按要求下载jar ,但是jar 包版本不好控制。有时候就会jar版本不同导致项目运行的结果也有差异,这样在团队开发中,在多个项目开发的是,jar包还要进行拷贝,可能也会出现版本还jar损坏的情况,所以一个能统一…...

服务高并发、高性能、高可用实现方案
服务高并发、高性能、高可用实现方案 软件开发的三高指标:高并发、高性能、高可用。 高并发方面要求QPS 大于 10万;高性能方面要求请求延迟小于 100 ms;高可用方面要高于 99.99%(4个9) 一、高并发: 高并发是现在互联网分布式框架设…...
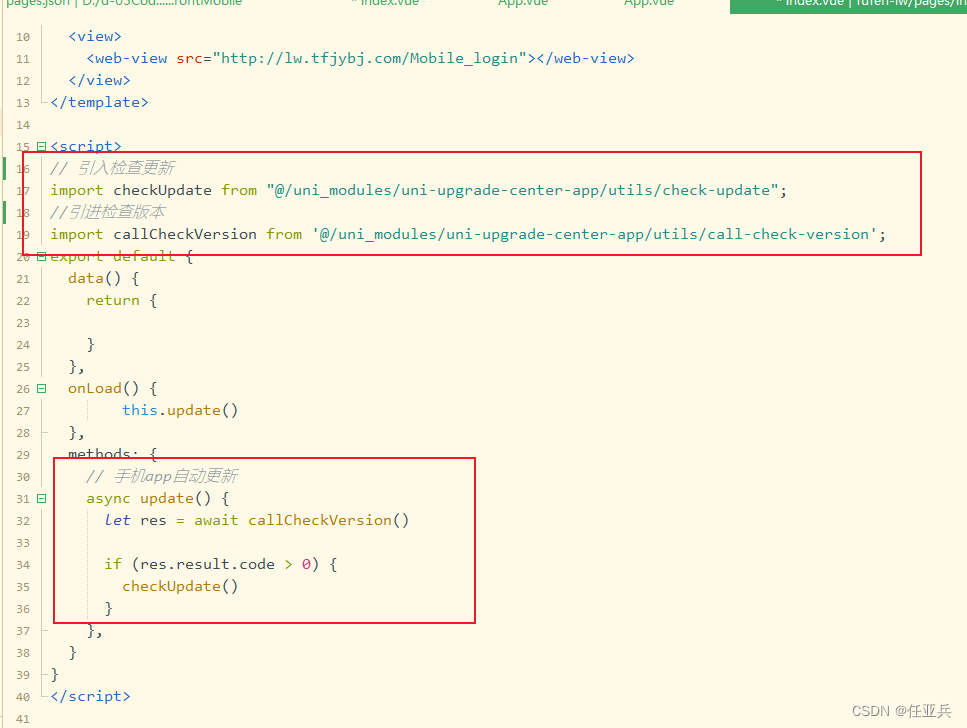
uniCloud在线升级APP配置教程
app在线升级背景实现思路流程流程背景 因用户需要添加手机h5页面来进数据操作实现思路流程 实现流程图流程 相关文档:帮助文档 https://uniapp.dcloud.net.cn/uniCloud/cf-functions.html 注册服务空间 https://unicloud.dcloud.net.cn/pages/login/login uni升级…...

idea常用的快捷键
idea常用的快捷键Alt回车 导入包,自动修正CtrlN 查找类CtrlShiftN 查找文件CtrlAltL 格式化代码CtrlAltO 优化导入的类和包AltInsert 生成代码(如get,set方法,构造函数等)CtrlE或者AltShiftC 最近更改的代码CtrlR 替换文本CtrlF 查找文本CtrlShiftSpace 自动补全代码Ctrl空格 代…...

全志V85x硬件设计大赛作品精选第一期,快来Pick你心目中的最佳方案
1、V853-智能交互摄像头开发板 该参赛作品基于全志V853开发板制作的一款类似眼镜外挂的小产品,可以对场景进行辅助识别,并通过云端交互实现物联网控制,进一步实现物联网与人机交互的融合。 开发板配置了摄像头和小屏幕接口,并外…...
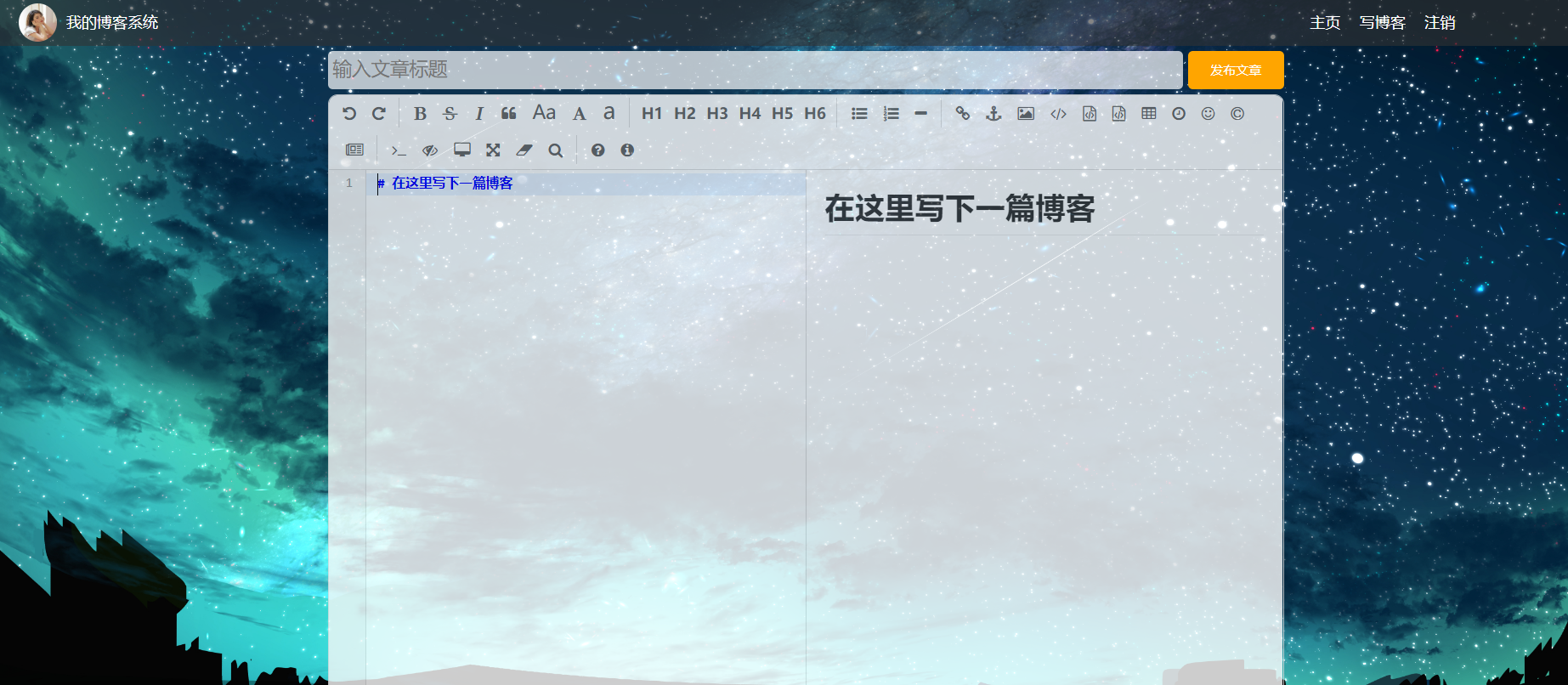
博客系统(界面设计)
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录实现博客列表页预期效果导航栏页面主体左右布局左侧区域右侧区域完整代码实现博客详情页预期效果导航栏 左侧右侧完整代码实现…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
