LeetCode 125. 验证回文串
更多题解尽在 https://sugar.matrixlab.dev/algorithm 每日更新。
组队打卡,更多解法等你一起来参与哦!
LeetCode 125. 验证回文串,难度简单。
双指针
解题思路:
- 遍历字符串,将所有大写字符转换为小写字符、并移除所有非字母数字字符;
- 使用左右指针比较字符,出现不同则直接返回 false
class Solution {public boolean isPalindrome(String s) {char[] chars = new char[s.length()];int left = 0, right = -1;// 将所有大写字符转换为小写字符、并移除所有非字母数字字符for (int i = 0; i < s.length(); ++i) {if (Character.isLetterOrDigit(s.charAt(i))) {chars[++right] = Character.toLowerCase(s.charAt(i));}}// 使用左右指针比较字符,出现不同则直接返回 falsewhile (left <= right) {if (chars[left] == chars[right]) {left++;right--;} else {return false;}}return true;}
}
相关文章:

LeetCode 125. 验证回文串
更多题解尽在 https://sugar.matrixlab.dev/algorithm 每日更新。 组队打卡,更多解法等你一起来参与哦! LeetCode 125. 验证回文串,难度简单。 双指针 解题思路: 遍历字符串,将所有大写字符转换为小写字符、并移除所…...

IT审计必看!对比旧版,CISA考试改版升级亮点和重点内容是什么?
官方通知,今年8月1日,CISA新版考纲正式上线,旧版在7月23日后就无法约考了。 艾威培训邀请了国内知名的IT审计CISA授课老师吴老师来为大家详细讲解CISA新版考纲的变化 目前第28th版教材只有英文版,中文版尚未发布。我们艾威经验丰…...

充电宝哪个牌子公认质量好?哪家充电宝好用?4款口碑好充电宝
在如今这个电子设备不离手的时代,充电宝成为了我们生活中的必备品。然而,面对市场上琳琅满目的充电宝品牌和型号,选择一款质量可靠、性能出色的充电宝并非易事。大家都在问:充电宝哪个牌子公认质量好?哪家充电宝好用&a…...

Python实现图像添加水印的方法
1. 简介 在日常图像处理中,为图片添加水印是一项常见任务。有多种方法和工具可供选择,而今天我们将专注于使用Python语言结合PIL库批量添加水印。 需要注意的是,所选用的图片格式不应为JPG或JPEG,因为这两种格式的图片不支持透明…...

MemFire Cloud: 一种全新定义后端即服务的解决方案
在这个快节奏的互联网时代,开发者们最希望的就是能够省时省力地完成项目,快速上线。然而,搭建服务、开发接口API、处理各种后端问题,往往让人头疼不已。别担心,现在有了MemFire Cloud,一款为懒人开发者量身…...
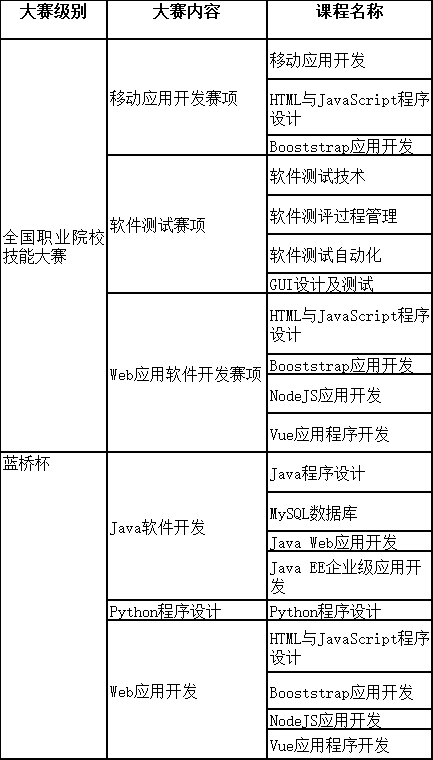
职业教育软件测试实验实训室建设应用案例
在信息化高速发展的今天,软件测试作为保障软件质量的关键环节,其重要性日益凸显。为满足职业教育对软件测试人才的培养需求,提高学生的实践能力和职业素养,唯众倾力打造了一款先进的软件测试实验实训室,并成功应用于多…...

如何判断一个js对象为数组类型
如何判断一个js对象为数组类型? 能想到的最常见的intanceof是吗?开始是这么认为,但是不是哈,看下面的解释,也没有太明白,暂且记住吧 综上,判断js对象为数组的两种方式 Array.isArray([]) // trueObject.prototype.toString.call([]) ‘[object Array]’ //true...

Nacos2.X 配置中心源码分析:客户端如何拉取配置、服务端配置发布客户端监听机制
文章目录 Nacos配置中心源码总流程图NacosClient源码分析获取配置注册监听器 NacosServer源码分析配置dump配置发布 Nacos配置中心源码 总流程图 Nacos2.1.0源码分析在线流程图 源码的版本为2.1.0 ,并在配置了下面两个启动参数,一个表示单机启动&#…...

phpstudy框架,window平台,如何开端口给局域网访问?
Windows平台上使用phpstudy框架开端口给同事访问,主要涉及到几个步骤:查看并确认本机IP地址、配置phpstudy及网站项目、开放防火墙端口以及确保同事能够通过局域网访问。以下是详细的步骤说明: 1. 查看并确认本机IP地址 首先,需…...

高性能Python网络框架实现网络应用详解
概要 Python作为一种广泛使用的编程语言,其简洁易读的语法和强大的生态系统,使得它在Web开发领域占据重要位置。高性能的网络框架是构建高效网络应用的关键因素之一。本文将介绍几个高性能的Python网络框架,详细描述它们的特点、使用场景及具体示例代码,帮助高效实现网络应…...

万字学习——DCU编程实战
参考资料 2.1 DCU软件栈(DCU ToolKit, DTK) DCU 开发与使用文档 (hpccube.com) DCU软件栈 DCU的软件栈—DCU Toolkit(DTK) HIP(Heterogeneous-Compute Interface for Portability)是AMD公司在2016年提出…...

Neo4j 图数据库 高级操作
Neo4j 图数据库 高级操作 文章目录 Neo4j 图数据库 高级操作1 批量添加节点、关系1.1 直接使用 UNWIND 批量创建关系1.2 使用 CSV 文件批量创建关系1.3 选择方法 2 索引2.1 创建单一属性索引2.2 创建组合属性索引2.3 创建全文索引2.4 列出所有索引2.5 删除索引2.6 注意事项 3 清…...

《RWKV》论文笔记
原文出处 [2305.13048] RWKV: Reinventing RNNs for the Transformer Era (arxiv.org) 原文笔记 What RWKV(RawKuv):Reinventing RNNs for the Transformer Era 本文贡献如下: 提出了 RWKV 网络架构,结合了RNNS 和Transformer 的优点,同…...
——显色指数(Ra))
相机光学(二十九)——显色指数(Ra)
显指Ra是衡量光源显色性的数值,表示光源对物体颜色的还原能力。显色性是指光源对物体颜色的呈现能力,即光源照射在同一颜色的物体上时,所呈现的颜色特性。通常用显色指数(CRI)来表示光源的显色性,而显指Ra是…...

【Swoole 的生命周期,文件描述符,协程数量,以及默认值】
目录 Swoole 的生命周期 Swoole 文件描述符(FD)缓存 Swoole设置协程的数量 Swoole 默认值 Swoole 是一个基于 PHP 的高性能网络通信引擎,它采用 C 编写,提供了协程和高性能的网络编程支持。Swoole 支持多种网络服务器和客户端…...

“不要卷模型,要卷应用”之高考志愿填报智能体
摘要:李总的发言深刻洞察了当前人工智能领域的发展趋势与核心价值所在,具有高度的前瞻性和实践性。“大家不要卷模型,要卷应用”这一观点强调了在当前人工智能领域,应该更加注重技术的实际应用而非单纯的技术竞赛或模型优化。个性…...

k8s离线部署芋道源码后端
目录 概述实践Dockerfilek8s部署脚本 概述 本篇将对 k8s离线部署芋道源码后端 进行详细的说明,对如何构建 Dockerfile,如何整合 Nginx,如何整合 ingress 进行实践。 相关文章:[nacos在k8s上的集群安装实践] k8s离线部署芋道源码前…...
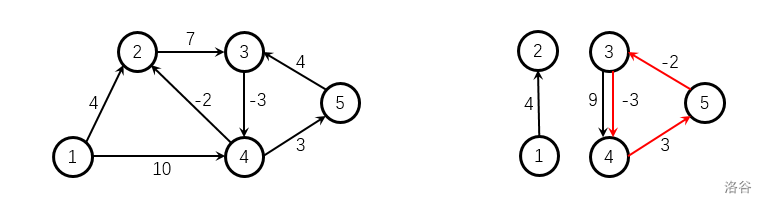
图论·Day01
P3371 P4779 P3371 【模板】单源最短路径(弱化版) 注意的点: 边有重复,选择最小边!对于SPFA算法容易出现重大BUG,没有负权值的边时不要使用!!! 70分代码 朴素板dijsk…...

hutool ExcelUtil 导出导入excel
引入依赖 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.8.15</version></dependency>文件导入 public void savelist(String filepath,String keyname){ExcelReader reader Exce…...

打卡第7天-----哈希表
继续坚持✊,我现在看到leetcode上的题不再没有思路了,真的是思路决定出路,在做题之前一定要把思路梳理清楚。 一、四数相加 leetcode题目编号:第454题.四数相加II 题目描述: 给定四个包含整数的数组列表 A , B , C , …...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
