【算法】十进制转换为二进制
目的:将十进制转换为二进制
思路:
首先我们手算的情况是通过求余数算出进制数,同样代码也是通过做除法和求余数的方式,除法是得出下一次的被除数,而求余数是得到进制数
代码:
#include<stdio.h>// 十进制转换为二进制,通过除法求余数
void getTwo(int n) {// res数组存放结果,div是要转换进制的数,mod是余数,flag是标记存放到数组的位置 int res[30]={0}; int div = n;int mod = 0;int flag;for (flag=0; div!=0; flag++) {// 如果要是十进制转换为八进制只需要修改下面的2为8即可,但是16进制需要重新写 mod = div % 2;div = div / 2;res[flag] = mod;
// res = res * 10 + mod;}// 逆序输出二进制数for (int i=flag-1; i>=0; i--) {printf("%d",res[i]);}
}
int main() {int n;scanf("%d",&n);getTwo(n); return 0;
}
相关文章:

【算法】十进制转换为二进制
目的:将十进制转换为二进制 思路: 首先我们手算的情况是通过求余数算出进制数,同样代码也是通过做除法和求余数的方式,除法是得出下一次的被除数,而求余数是得到进制数 代码: #include<stdio.h>/…...

Postman中的API安全堡垒:全面安全性测试指南
🛡️ Postman中的API安全堡垒:全面安全性测试指南 在当今的数字化世界中,API安全性是保护数据和系统不可或缺的一环。Postman作为API开发和测试的领先工具,提供了多种功能来帮助开发者进行API安全性测试。本文将深入探讨如何在Po…...

学圣学最终的目的是:达到思无邪的状态( 纯粹、思想纯正、积极向上 )
学圣学最终的目的是:达到思无邪的状态( 纯粹、思想纯正、积极向上 ) 中华民族,一直以来,教学都是以追随圣学为目标,所以中华文化也叫圣学文化,是最高深的上等学问; 圣人那颗心根本…...

JS进阶-构造函数
学习目标: 掌握构造函数 学习内容: 构造函数 构造函数: 封装是面向对象思想中比较重要的一部分,js面向对象可以通过构造函数实现的封装。 同样的将变量和函数组合到了一起并能通过this实现数据的共享,所不同的是借助…...

使用Spring Boot和Couchbase实现NoSQL数据库
使用Spring Boot和Couchbase实现NoSQL数据库 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 一、引言 NoSQL数据库越来越受到开发者的欢迎,特别是…...

【数据库】Redis主从复制、哨兵模式、集群
目录 一、Redis的主从复制 1.1 主从复制的架构 1.2 主从复制的作用 1.3 注意事项 1.4 主从复制用到的命令 1.5 主从复制流程 1.6 主从复制实现 1.7 结束主从复制 1.8 主从复制优化配置 二、哨兵模式 2.1 哨兵模式原理 2.2 哨兵的三个定时任务 2.3 哨兵的结构 2.4 哨…...

C基础day8
一、思维导图 二、课后习题 #include<myhead.h> #define Max_Stu 100 //函数声明 //学生信息录入函数 void Enter_stu(int *Num_Stu,char Stu_name[][50],int Stu_score[]); //查看学生信息 void Print_stu(int Num_Stu,char Stu_name[][50],int Stu_score[]); //求出成绩…...
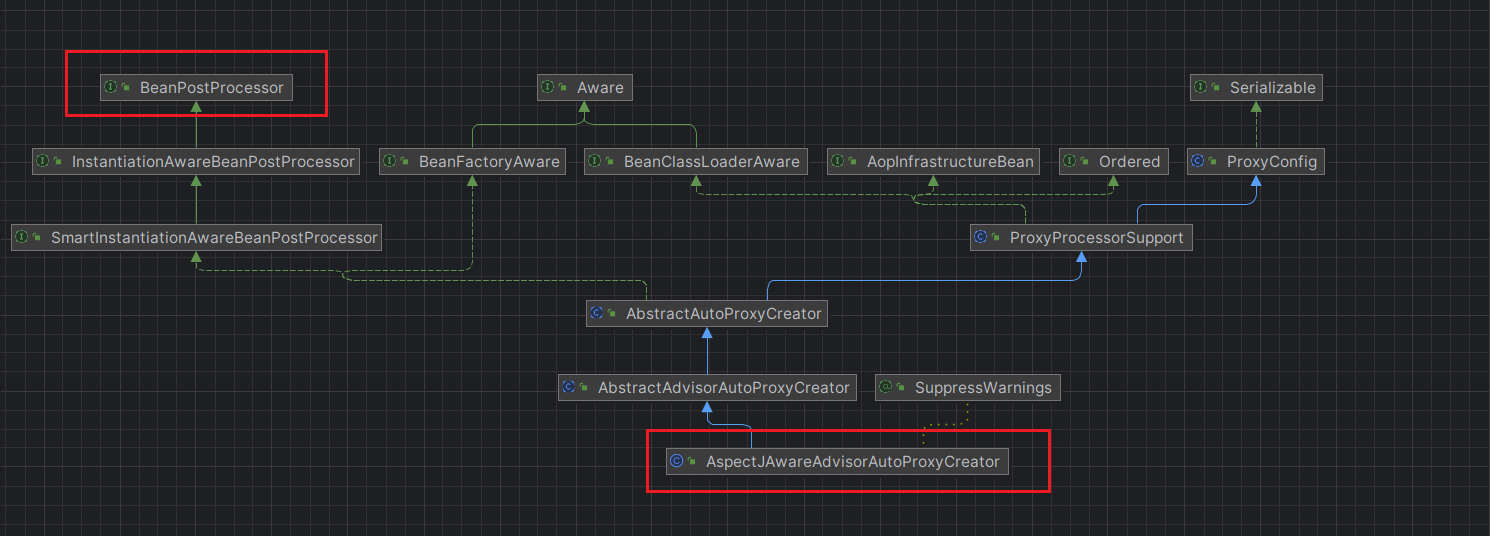
【Spring成神之路】老兄,来一杯Spring AOP源码吗?
文章目录 一、引言二、Spring AOP的使用三、Spring AOP的组件3.1 Pointcut源码3.2 Advice源码3.3 Advisor源码3.4 Aspect源码 四、Spring AOP源码刨析4.1 configureAutoProxyCreator源码解析4.2 parsePointcut源码解析4.3 parseAdvisor源码解析4.4 parseAspect源码解析4.5 小总…...

轻松理解c++17的string_view
文章目录 轻松理解c17的string_view设计初衷常见用法构造 std::string_view常用操作作为函数参数 注意事项总结 轻松理解c17的string_view std::string_view 是 C17 引入的一个轻量级、不拥有(non-owning)的字符串视图类。它的设计初衷是提供一种高效、…...
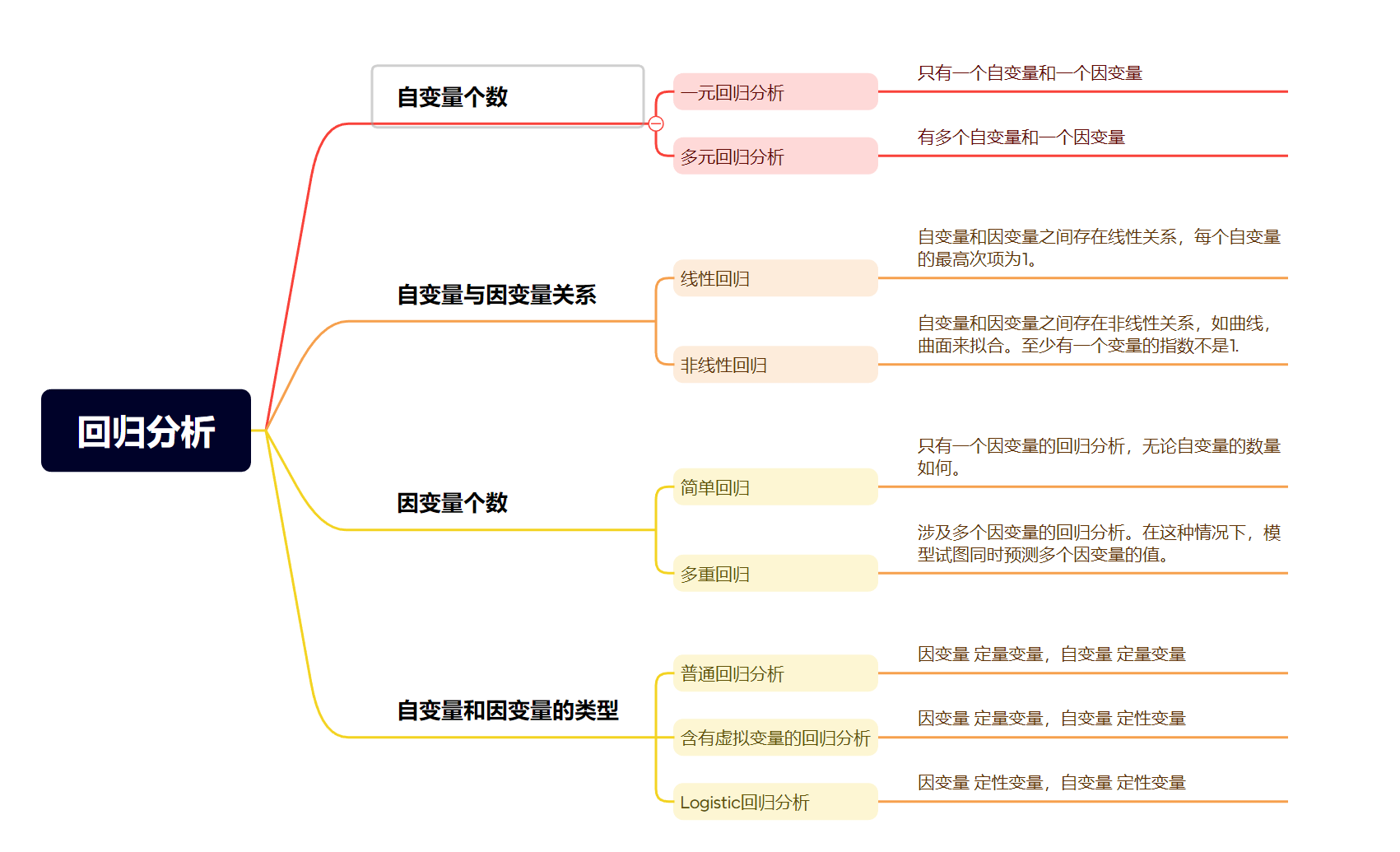
【机器学习理论基础】回归模型定义和分类
定义 回归分析是研究自变量与因变量之间数量变化关系的一种分析方法,它主要是通过因变量 Y Y Y与影响它的自变量 X i X_i Xi 之间的回归模型,衡量自变量 X i X_i Xi 对因变量 Y Y Y 的影响能力的,进而可以用来预测因变量Y的发展趋势。…...

探讨4层代理和7层代理行为以及如何获取真实客户端IP
准备工作 实验环境 IP角色192.168.1.100客户端请求IP192.168.1.100python 启动的HTTP服务192.168.1.102nginx服务192.168.1.103haproxy 服务 HTTP服务 这是一个简单的HTTP服务,主要打印HTTP报文用于分析客户端IP #!/usr/bin/env python # coding: utf-8import …...

java算法day11
二叉树的递归遍历二叉树的非递归遍历写法层序遍历 递归怎么写? 按照三要素可以保证写出正确的递归算法: 1.确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且…...

linux下安装cutecom串口助手;centos安装cutecom串口助手;rpm安装包安装cutecom串口助手
在支持apt-get的系统下安装 在终端命令行中输入: sudo apt-get install cutecom 安装好后输入 sudo cutecom 就可以了 关于如何使用,可以看这个https://www.cnblogs.com/xingboy/p/14388610.html 如果你的电脑不支持apt-get。 那我们就通过安装包…...

2024年信息系统项目管理师2批次上午客观题参考答案及解析(1)
1、关于收集需求管理过程及相关技术的描述,正确的是() A.需求跟踪矩阵是把产品需求从其来源链接到能满足需求的可交付成果的一种表格 B.原型法是一种结构化的头脑风暴形式,通过投票排列最有用的创意 C&am…...

Xinstall揭秘:APP推广数据背后的真相,让你的营销更精准!
在这个移动互联网时代,APP如同雨后春笋般涌现,但如何在这片红海中脱颖而出,成为每一个开发者与运营者面临的共同难题。其中,APP推广统计作为衡量营销效果、优化推广策略的关键环节,更是不可忽视的一环。今天࿰…...

科研绘图系列:R语言小提琴图(Violin Plot)
介绍 小提琴图(Violin Plot)是一种结合了箱线图和密度图的图表,它能够展示数据的分布密度和分布形状。以下是对小提琴图的详细解释: 小提琴图能表达: 数据分布:小提琴图通过在箱线图的两侧绘制曲线来展示数据的分布密度,曲线的宽度表示数据点的密度。集中趋势:箱线图部…...

【Vite】修改构建后的 index.html 文件名
在 Vite 项目中,默认构建 index.html 。但有时候我们需要修改 index.html 为其他文件名,比如 index-{时间戳}.html 。 我们可以这样配置 vite.config.js: import { defineConfig } from vite; import type { PluginOption } from vite;// 自…...

解决IDEA每次新建项目都需要重新配置maven的问题
每次打开IDEA都要重新配置maven,这是因为在DEA中分为项目设置和全局设置,这个时候我们就需要去到全局中设置maven了。我用的是IntelliJ IDEA 2023.3.4 (Ultimate Edition),以此为例。 第一步:打开一个空的IDEA,选择左…...

论文学习_Getafix: learning to fix bugs automatically
1. 引言 研究背景:现代生产代码库极其复杂并且不断更新。静态分析器可以帮助开发人员发现代码中的潜在问题(在本文的其余部分中称为错误),这对于在这些大型代码库中保持高代码质量是必要的。虽然通过静态分析尽早发现错误是有帮助的,但修复这些错误的问题在实践中仍然主要…...

Xilinx FPGA:vivado关于真双端口的串口传输数据的实验
一、实验内容 用一个真双端RAM,端口A和端口B同时向RAM里写入数据0-99,A端口读出单数并存入单端口RAM1中,B端口读出双数并存入但端口RAM2中,当检测到按键1到来时将RAM1中的单数读出显示到PC端,当检测到按键2到来时&…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
