火柴棒图python绘画
使用Python绘制二项分布的概率质量函数(PMF)
在这篇博客中,我们将探讨如何使用Python中的scipy库和matplotlib库来绘制二项分布的概率质量函数(PMF)。二项分布是统计学中常见的离散概率分布,描述了在固定次数的独立试验中,成功次数的分布情况。
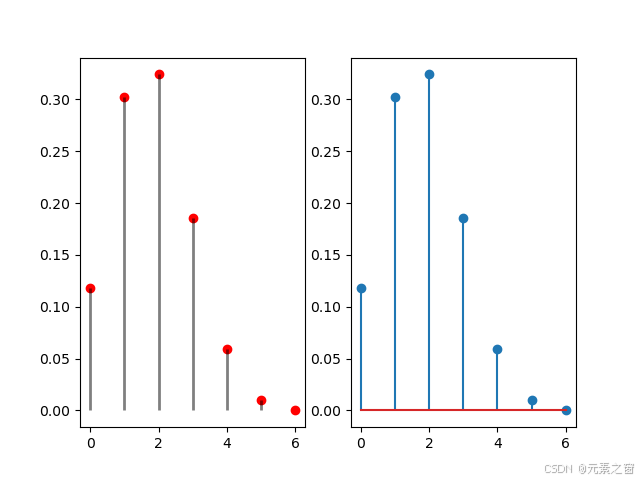
代码示例
以下是一个完整的代码示例,展示了如何绘制二项分布的PMF:
from scipy.stats import binom
import pylab as plt# 定义二项分布的参数
n = 6 # 试验次数
p = 0.3 # 成功概率# 生成可能的成功次数
x = plt.arange(7) # 0到6的整数
y = binom.pmf(x, n, p) # 计算每个成功次数的概率# 创建第一个子图:竖线图
plt.subplot(121)
plt.plot(x, y, 'ro') # 绘制红色圆点
plt.vlines(x, 0, y, 'k', lw=2, alpha=0.5) # 绘制竖线
plt.xlabel('成功次数')
plt.ylabel('概率')
plt.title('竖线图')# 创建第二个子图:茎叶图
plt.subplot(122)
plt.stem(x, y, use_line_collection=True) # 绘制茎叶图
plt.xlabel('成功次数')
plt.ylabel('概率')
plt.title('茎叶图')# 保存图像并显示
plt.savefig("figure9_2.png", dpi=500)
plt.show()
代码解释
-
导入库:
from scipy.stats import binom import pylab as plt我们导入了
scipy.stats中的binom模块来处理二项分布,并导入pylab作为绘图工具。 -
定义参数:
n = 6 # 试验次数 p = 0.3 # 成功概率这里我们定义了二项分布的参数:试验次数
n和成功概率p。 -
生成数据:
x = plt.arange(7) # 0到6的整数 y = binom.pmf(x, n, p) # 计算每个成功次数的概率我们生成了可能的成功次数
x(从0到6),并计算了每个成功次数的概率y。 -
绘制竖线图:
plt.subplot(121) plt.plot(x, y, 'ro') # 绘制红色圆点 plt.vlines(x, 0, y, 'k', lw=2, alpha=0.5) # 绘制竖线 plt.xlabel('成功次数') plt.ylabel('概率') plt.title('竖线图')在第一个子图中,我们绘制了竖线图,使用红色圆点表示每个成功次数的概率,并用黑色竖线从x轴延伸到每个点。
-
绘制茎叶图:
plt.subplot(122) plt.stem(x, y, use_line_collection=True) # 绘制茎叶图 plt.xlabel('成功次数') plt.ylabel('概率') plt.title('茎叶图')在第二个子图中,我们绘制了茎叶图,使用竖线和圆点来表示每个成功次数的概率。
-
保存并显示图像:
plt.savefig("figure9_2.png", dpi=500) plt.show()最后,我们将图像保存为高分辨率的PNG文件,并显示图像。
总结
通过这篇博客,我们学习了如何使用Python绘制二项分布的概率质量函数(PMF)。我们使用了scipy库来计算二项分布的概率,并使用matplotlib库绘制了竖线图和茎叶图。这些图表可以帮助我们更好地理解二项分布的特性和行为。
希望这篇博客对你有所帮助!如果你有任何问题或建议,欢迎在评论区留言。谢谢阅读!
相关文章:

火柴棒图python绘画
使用Python绘制二项分布的概率质量函数(PMF) 在这篇博客中,我们将探讨如何使用Python中的scipy库和matplotlib库来绘制二项分布的概率质量函数(PMF)。二项分布是统计学中常见的离散概率分布,描述了在固定次…...

Nginx七层(应用层)反向代理:UWSGI代理uwsgi_pass篇
Nginx七层(应用层)反向代理 UWSGI代理uwsgi_pass篇 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this a…...

Effective C++笔记之二十一:One Definition Rule(ODR)
ODR细节有点复杂,跨越各种情况。基本内容如下: ●普通(非模板)的noninline函数和成员函数、noninline全局变量、静态数据成员在整个程序中都应当只定义一次。 ●class类型(包括structs和unions)、模板&…...

探索未来:Transformer模型在智能环境监测的革命性应用
探索未来:Transformer模型在智能环境监测的革命性应用 在当今数字化时代,环境监测正逐渐从传统的人工检测方式转变为智能化、自动化的系统。Transformer模型,作为深度学习领域的一颗新星,其在自然语言处理(NLP&#x…...

Nginx中文URL请求404
这两天正在搞我的静态网站。方案是:从思源笔记Markdown笔记,用MkOcs build成静态网站,上传到到Nginx服务器。遇到一个问题:URL含有中文会404,全英文URL则正常访问。 比如: 设置了utf-8 ht…...
介绍)
33. 动量法(Momentum)介绍
1. 背景知识 在深度学习的优化过程中,梯度下降法(Gradient Descent, GD)是最基本的方法。然而,基本的梯度下降法在实际应用中存在收敛速度慢、容易陷入局部最小值以及在高维空间中振荡较大的问题。为了解决这些问题,人…...

Python | Leetcode Python题解之第228题汇总区间
题目: 题解: class Solution:def summaryRanges(self, nums: List[int]) -> List[str]:def f(i: int, j: int) -> str:return str(nums[i]) if i j else f{nums[i]}->{nums[j]}i 0n len(nums)ans []while i < n:j iwhile j 1 < n …...

物联网应用,了解一点 WWAN全球网络标准
WWAN/蜂窝无线电认证,对跨地区应用场景,特别重要。跟随全球业务的脚步,我们像大唐先辈一样走遍全球业务的时候,了解一点全球化的 知识信息,就显得有那么点意义。 NA (北美):美国和加…...
如何指定多块GPU卡进行训练-数据并行
训练代码: train.py import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader, Dataset import torch.nn.functional as F# 假设我们有一个简单的文本数据集 class TextDataset(Dataset):def __init__(self, te…...

RK3568笔记三十三: helloworld 驱动测试
若该文为原创文章,转载请注明原文出处。 报着学习态度,接下来学习驱动是如何使用的,从简单的helloworld驱动学习起。 开始编写第一个驱动程序—helloworld 驱动。 一、环境 1、开发板:正点原子的ATK-DLRK3568 2、系统…...

【智能制造-14】机器视觉软件
CCD相机和COMS相机? CCD(Charge-Coupled Device)相机和CMOS(Complementary Metal-Oxide-Semiconductor)相机是两种常见的数字图像传感器技术,用于捕捉和处理图像。 CCD相机: CCD相机使用一种称为CCD的光电…...
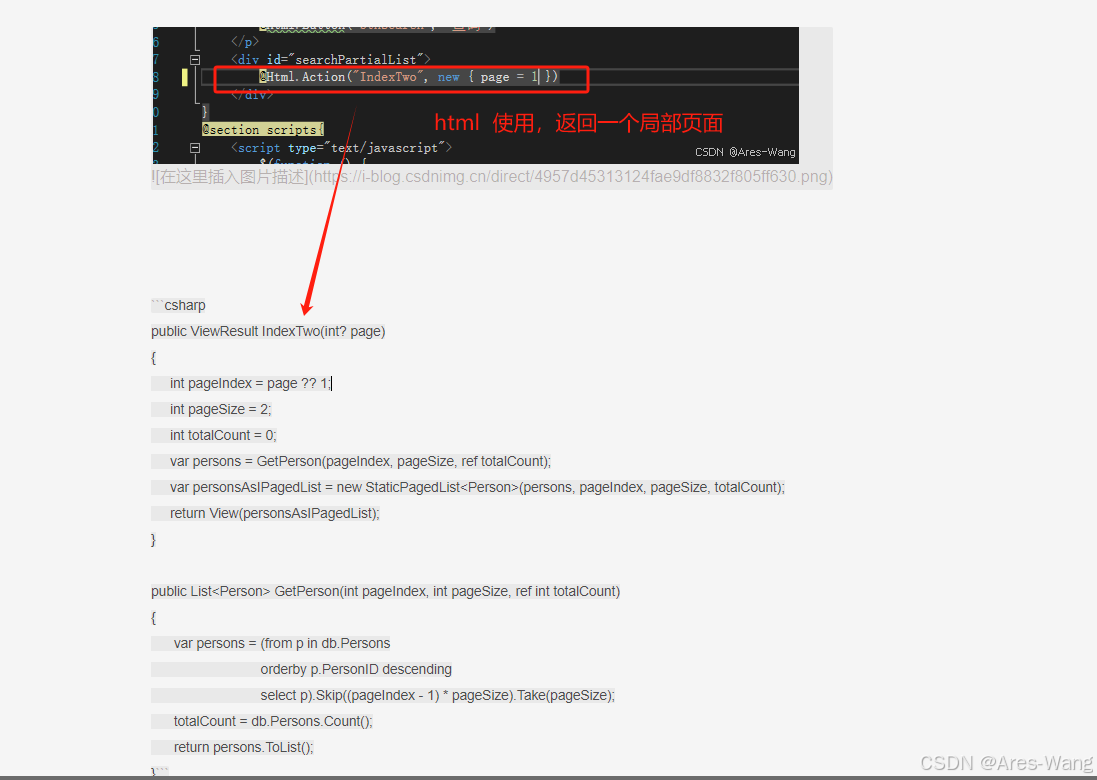
MVC分页
public ActionResult Index(int ? page){IPagedList<EF.ACCOUNT> userPagedList;using (EF.eMISENT content new EF.eMISENT()){第几页int pageNumber page ?? 1;每页数据条数,这个可以放在配置文件中int pageSize 10;//var infoslist.C660List.OrderBy(…...

webGL可用的14种3D文件格式,但要具体问题具体分析。
hello,我威斯数据,你在网上看到的各种炫酷的3d交互效果,背后都必须有三维文件支撑,就好比你网页的时候,得有设计稿源文件一样。WebGL是一种基于OpenGL ES 2.0标准的3D图形库,可以在网页上实现硬件加速的3D图…...
HybridCLR原理中的重点总结
序言 该文章以一个新手的身份,讲一下自己学习的经过,大家更快的学习HrbirdCLR。 我之前的两个Unity项目中,都使用到了热更新功能,而热更新的技术栈都是用的HybridCLR。 第一个项目本身虽然已经集成好了热更逻辑(使用…...
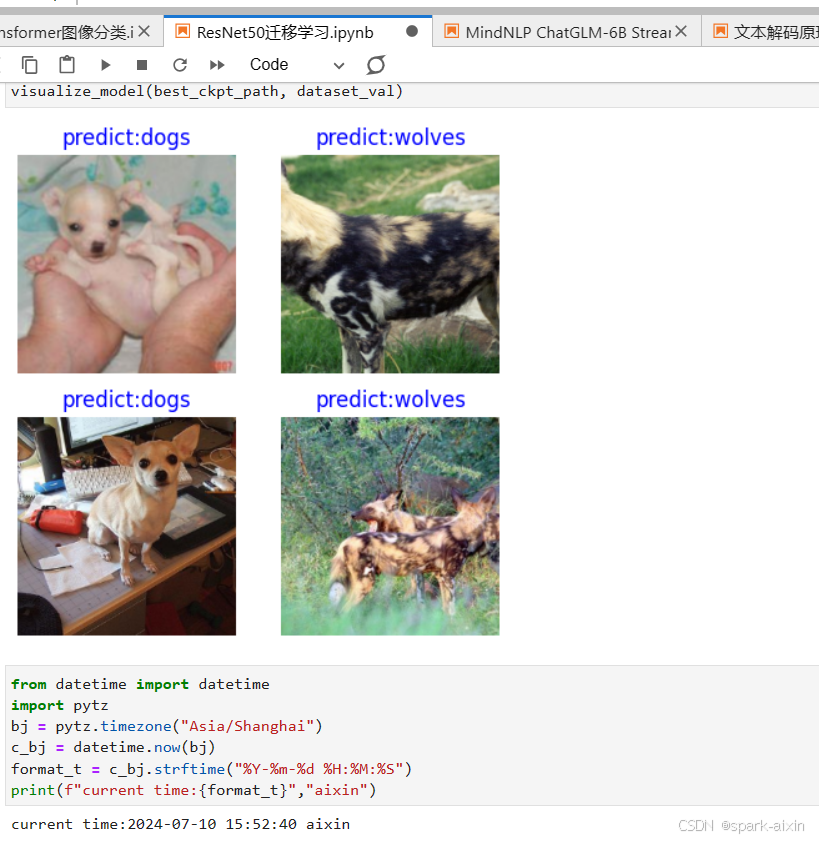
昇思学习打卡-14-ResNet50迁移学习
文章目录 数据集可视化预训练模型的使用部分实现 推理 迁移学习:在一个很大的数据集上训练得到一个预训练模型,然后使用该模型来初始化网络的权重参数或作为固定特征提取器应用于特定的任务中。本章学习使用的是前面学过的ResNet50,使用迁移学…...
)
软件开发面试题C#,.NET知识点(续)
1.C#中的封装是什么,以及它的重要性。 封装(Encapsulation) 是面向对象编程(OOP)的一个基本概念。它指的是将对象的状态(属性)和行为(方法)绑定在一起,并且将…...

2019年美赛题目Problem A: Game of Ecology
本题分析: 本题想要要求从实际生物角度出发,对权力游戏中龙这种虚拟生物的生态环境和生物特性进行建模,感觉属于比较开放类型的题目,重点在于参考生物的选择,龙虽然是虚拟的但是龙的生态特性可以参考目前生物圈里存在…...

沙龙回顾|MongoDB如何充当企业开发加速器?
数据不仅是企业发展转型的驱动力,也是开发者最棘手的问题。前日,MongoDB携手阿里云、NineData在杭州成功举办了“数据驱动,敏捷前行——MongoDB企业开发加速器”技术沙龙。此次活动吸引了来自各行各业的专业人员,共同探讨MongoDB的…...

云端编码:将您的技术API文档安全存储在iCloud的最佳实践
云端编码:将您的技术API文档安全存储在iCloud的最佳实践 作为一名技术专业人士,管理不断增长的API文档库是一项挑战。iCloud提供了一个无缝的解决方案,允许您在所有设备上存储、同步和访问您的个人技术API文档。本文将指导您如何在iCloud中高…...

在Spring Boot项目中集成单点登录解决方案
在Spring Boot项目中集成单点登录解决方案 大家好,我是微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在现代的企业应用中,单点登录(Single Sign-On, SSO)解决方案是确保用户…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
