【排序 - 选择排序优化版(利用堆排序)】
结合选择排序和堆排序的思路,可以通过利用堆数据结构来优化选择排序的过程,使得排序算法更加高效。在这种结合中,我们利用堆的特性来快速定位和选择未排序部分的最小元素,避免了选择排序中每次线性搜索的开销。
选择排序和堆排序结合的思路
选择排序的基本思想是每次从未排序的部分选择最小(或最大)的元素,放到已排序部分的末尾。结合堆排序的思路,我们可以利用最小堆来维护未排序部分的元素,每次从堆顶取出最小元素,放入已排序部分,然后调整堆,以保持堆的性质。
实现步骤
- 建立最小堆:将待排序的数组建立成一个最小堆。
- 选择最小元素:从堆顶(最小值)开始选择,将其放入已排序部分。
- 维护堆的性质:每次选择操作后,需要调整堆,使得剩余的元素依然构成最小堆。
- 重复以上步骤:直到所有元素都被排序。
C语言代码实现
下面是利用C语言实现结合选择排序和堆排序思路的示例代码:
#include <stdio.h>// 函数:对数组的子树以根节点 i 进行堆化,n 是堆的大小
void heapify(int arr[], int n, int i) {int smallest = i; // 初始化最小值索引为 iint left = 2 * i + 1; // 左子节点索引为 2*i + 1int right = 2 * i + 2; // 右子节点索引为 2*i + 2// 如果左子节点比根节点小if (left < n && arr[left] < arr[smallest])smallest = left;// 如果右子节点比当前最小值小if (right < n && arr[right] < arr[smallest])smallest = right;// 如果最小值不是根节点if (smallest != i) {// 交换最小值和根节点int temp = arr[i];arr[i] = arr[smallest];arr[smallest] = temp;// 递归调整受影响的子树heapify(arr, n, smallest);}
}// 函数:进行堆排序
void heapSort(int arr[], int n) {// 构建堆(重新排列数组)for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);// 依次从堆中提取元素for (int i = n - 1; i > 0; i--) {// 将当前根节点移至末尾int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 对剩余堆进行堆化heapify(arr, i, 0);}
}// 函数:利用堆排序原理执行选择排序
void selectionHeapSort(int arr[], int n) {// 从数组构建最小堆heapSort(arr, n);// 现在 arr[0] 包含最小元素,将其移到末尾并重复for (int i = 0; i < n; i++) {// 交换 arr[0] 和 arr[i]int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 重建堆,排除已排序的最后一个元素heapify(arr, i, 0);}
}// 函数:打印数组
void printArray(int arr[], int n) {for (int i = 0; i < n; ++i)printf("%d ", arr[i]);printf("\n");
}// 主函数:测试以上功能
int main() {int arr[] = {12, 11, 13, 5, 6, 7};int n = sizeof(arr) / sizeof(arr[0]);printf("原始数组:\n");printArray(arr, n);selectionHeapSort(arr, n);printf("选择和堆排序结合后的排序数组:\n");printArray(arr, n);return 0;
}
}
示例说明
在上面的代码中:
heapify()函数用于维护堆的性质。heapSort()函数用于对数组进行堆排序。selectionHeapSort()函数结合了选择排序和堆排序的思路,通过建立最小堆和每次选择操作来实现排序。main()函数中展示了如何使用selectionHeapSort()函数对数组进行排序,并输出排序后的结果。
这种结合选择排序和堆排序的方法利用了堆的优势,使得选择过程更高效,从而提升了整体排序算法的性能。
相关文章:
】)
【排序 - 选择排序优化版(利用堆排序)】
结合选择排序和堆排序的思路,可以通过利用堆数据结构来优化选择排序的过程,使得排序算法更加高效。在这种结合中,我们利用堆的特性来快速定位和选择未排序部分的最小元素,避免了选择排序中每次线性搜索的开销。 选择排序和堆排序…...

PHP编程开发工具有哪些?
PHP的开发工具种类繁多,涵盖了从集成开发环境(IDE)、代码编辑器、调试器到版本控制工具和数据库管理工具等多个方面。以下是一些常见的PHP开发工具: 1. 集成开发环境(IDE) PhpStorm:由JetBrai…...
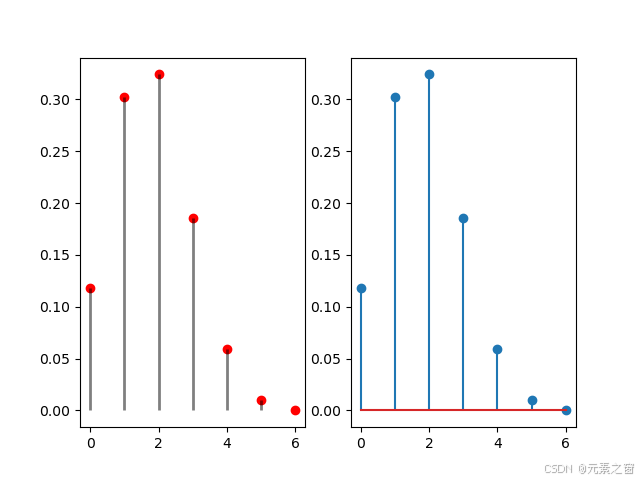
火柴棒图python绘画
使用Python绘制二项分布的概率质量函数(PMF) 在这篇博客中,我们将探讨如何使用Python中的scipy库和matplotlib库来绘制二项分布的概率质量函数(PMF)。二项分布是统计学中常见的离散概率分布,描述了在固定次…...

Nginx七层(应用层)反向代理:UWSGI代理uwsgi_pass篇
Nginx七层(应用层)反向代理 UWSGI代理uwsgi_pass篇 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this a…...

Effective C++笔记之二十一:One Definition Rule(ODR)
ODR细节有点复杂,跨越各种情况。基本内容如下: ●普通(非模板)的noninline函数和成员函数、noninline全局变量、静态数据成员在整个程序中都应当只定义一次。 ●class类型(包括structs和unions)、模板&…...

探索未来:Transformer模型在智能环境监测的革命性应用
探索未来:Transformer模型在智能环境监测的革命性应用 在当今数字化时代,环境监测正逐渐从传统的人工检测方式转变为智能化、自动化的系统。Transformer模型,作为深度学习领域的一颗新星,其在自然语言处理(NLP&#x…...

Nginx中文URL请求404
这两天正在搞我的静态网站。方案是:从思源笔记Markdown笔记,用MkOcs build成静态网站,上传到到Nginx服务器。遇到一个问题:URL含有中文会404,全英文URL则正常访问。 比如: 设置了utf-8 ht…...
介绍)
33. 动量法(Momentum)介绍
1. 背景知识 在深度学习的优化过程中,梯度下降法(Gradient Descent, GD)是最基本的方法。然而,基本的梯度下降法在实际应用中存在收敛速度慢、容易陷入局部最小值以及在高维空间中振荡较大的问题。为了解决这些问题,人…...

Python | Leetcode Python题解之第228题汇总区间
题目: 题解: class Solution:def summaryRanges(self, nums: List[int]) -> List[str]:def f(i: int, j: int) -> str:return str(nums[i]) if i j else f{nums[i]}->{nums[j]}i 0n len(nums)ans []while i < n:j iwhile j 1 < n …...

物联网应用,了解一点 WWAN全球网络标准
WWAN/蜂窝无线电认证,对跨地区应用场景,特别重要。跟随全球业务的脚步,我们像大唐先辈一样走遍全球业务的时候,了解一点全球化的 知识信息,就显得有那么点意义。 NA (北美):美国和加…...
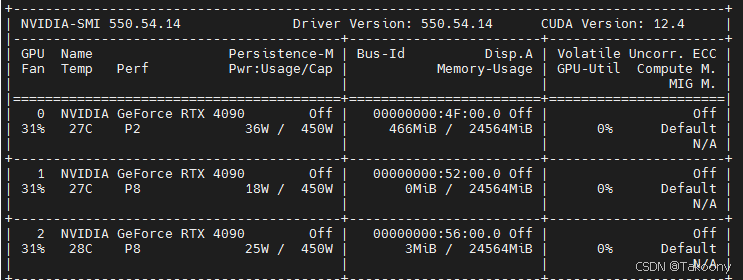
如何指定多块GPU卡进行训练-数据并行
训练代码: train.py import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader, Dataset import torch.nn.functional as F# 假设我们有一个简单的文本数据集 class TextDataset(Dataset):def __init__(self, te…...

RK3568笔记三十三: helloworld 驱动测试
若该文为原创文章,转载请注明原文出处。 报着学习态度,接下来学习驱动是如何使用的,从简单的helloworld驱动学习起。 开始编写第一个驱动程序—helloworld 驱动。 一、环境 1、开发板:正点原子的ATK-DLRK3568 2、系统…...

【智能制造-14】机器视觉软件
CCD相机和COMS相机? CCD(Charge-Coupled Device)相机和CMOS(Complementary Metal-Oxide-Semiconductor)相机是两种常见的数字图像传感器技术,用于捕捉和处理图像。 CCD相机: CCD相机使用一种称为CCD的光电…...
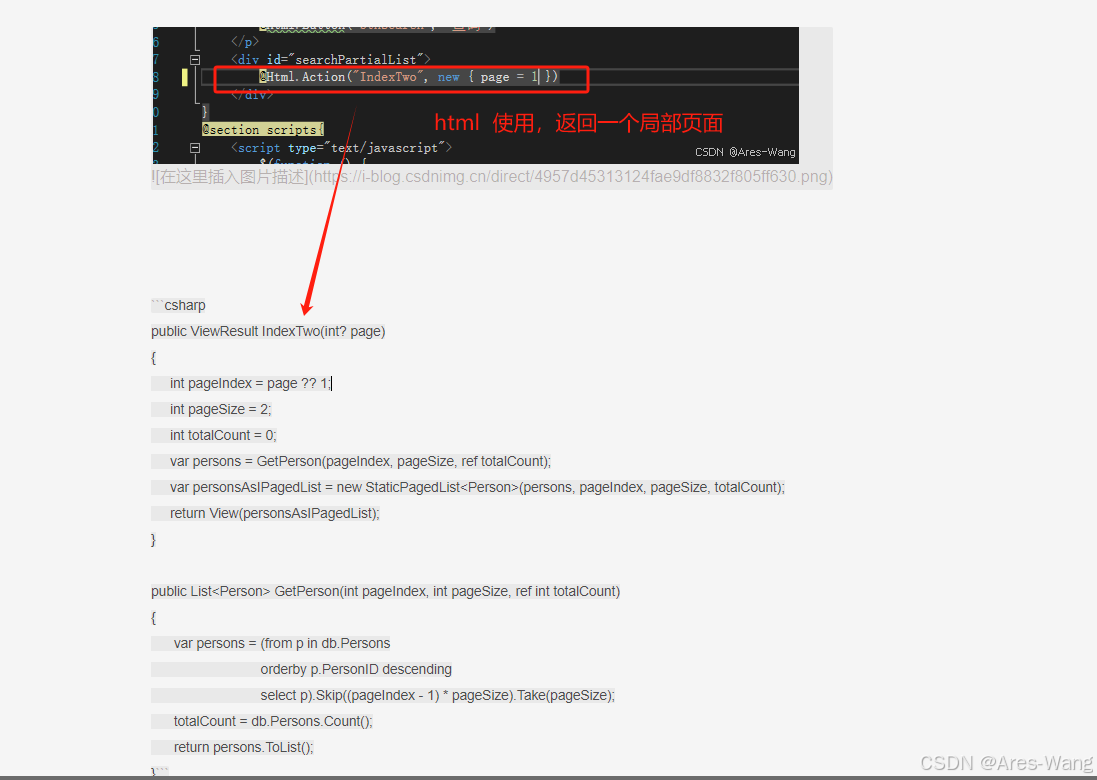
MVC分页
public ActionResult Index(int ? page){IPagedList<EF.ACCOUNT> userPagedList;using (EF.eMISENT content new EF.eMISENT()){第几页int pageNumber page ?? 1;每页数据条数,这个可以放在配置文件中int pageSize 10;//var infoslist.C660List.OrderBy(…...

webGL可用的14种3D文件格式,但要具体问题具体分析。
hello,我威斯数据,你在网上看到的各种炫酷的3d交互效果,背后都必须有三维文件支撑,就好比你网页的时候,得有设计稿源文件一样。WebGL是一种基于OpenGL ES 2.0标准的3D图形库,可以在网页上实现硬件加速的3D图…...
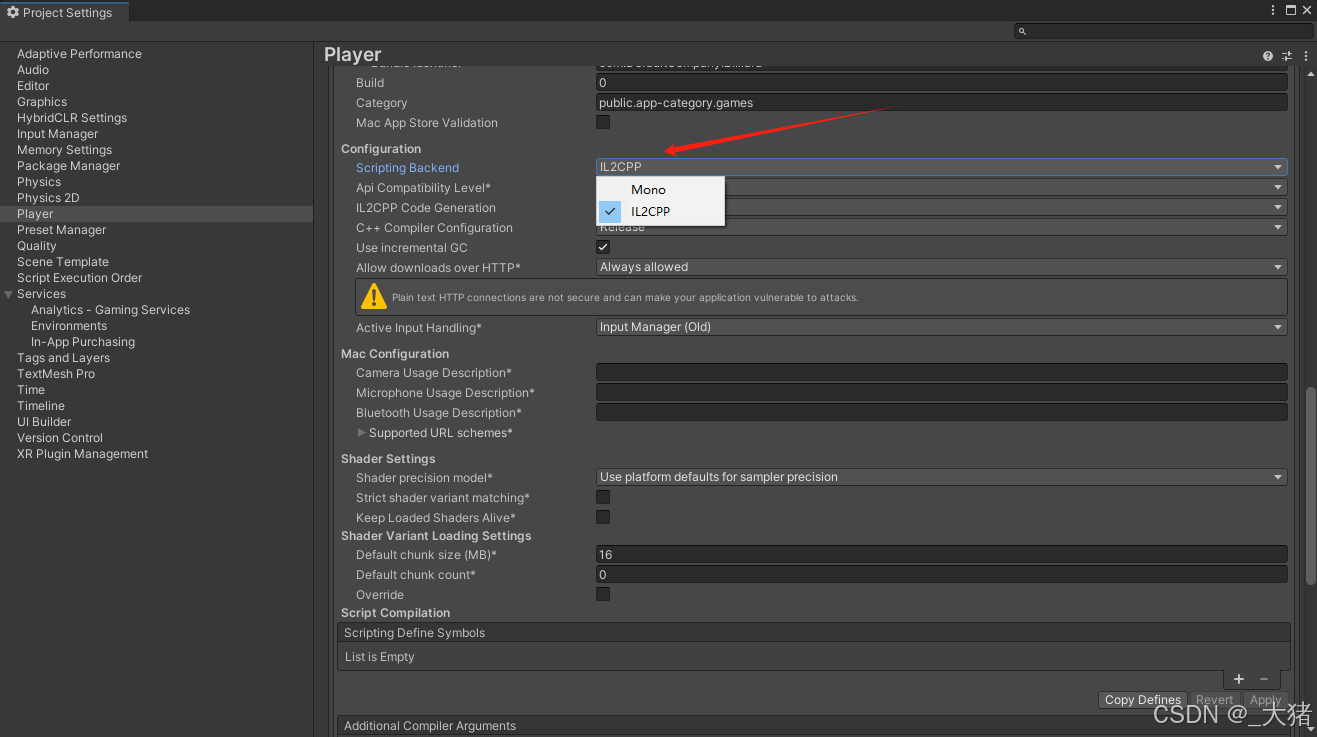
HybridCLR原理中的重点总结
序言 该文章以一个新手的身份,讲一下自己学习的经过,大家更快的学习HrbirdCLR。 我之前的两个Unity项目中,都使用到了热更新功能,而热更新的技术栈都是用的HybridCLR。 第一个项目本身虽然已经集成好了热更逻辑(使用…...
昇思学习打卡-14-ResNet50迁移学习
文章目录 数据集可视化预训练模型的使用部分实现 推理 迁移学习:在一个很大的数据集上训练得到一个预训练模型,然后使用该模型来初始化网络的权重参数或作为固定特征提取器应用于特定的任务中。本章学习使用的是前面学过的ResNet50,使用迁移学…...
)
软件开发面试题C#,.NET知识点(续)
1.C#中的封装是什么,以及它的重要性。 封装(Encapsulation) 是面向对象编程(OOP)的一个基本概念。它指的是将对象的状态(属性)和行为(方法)绑定在一起,并且将…...

2019年美赛题目Problem A: Game of Ecology
本题分析: 本题想要要求从实际生物角度出发,对权力游戏中龙这种虚拟生物的生态环境和生物特性进行建模,感觉属于比较开放类型的题目,重点在于参考生物的选择,龙虽然是虚拟的但是龙的生态特性可以参考目前生物圈里存在…...

沙龙回顾|MongoDB如何充当企业开发加速器?
数据不仅是企业发展转型的驱动力,也是开发者最棘手的问题。前日,MongoDB携手阿里云、NineData在杭州成功举办了“数据驱动,敏捷前行——MongoDB企业开发加速器”技术沙龙。此次活动吸引了来自各行各业的专业人员,共同探讨MongoDB的…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
