C++:红黑树
红黑树的概念
红黑树是一棵二叉搜索树,但是红黑树通过增加一个存储位表示结点的颜色RED或BLACK。通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出2倍,因而是接近平衡的。
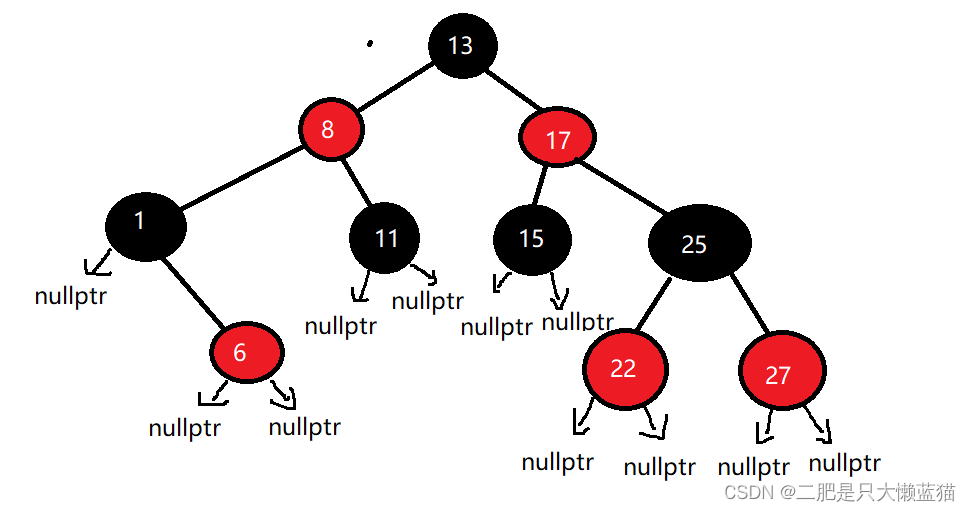
红黑树的性质
⭐1.每个节点不是红色就是黑色。
⭐2.根节点是黑色的。
⭐3.如果一个节点是红色的,则它的两个孩子结点是黑色的。也就意味着,红黑树没有连续的红色节点。
⭐4.对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。也就是说每条路径都有相同数量的黑色节点。
⭐5.每个叶子结点都是黑色的(此处的叶子结点指的是空结点。
从性质上分析红黑树的近似平衡
一颗红黑树最短的路径是这条路径全黑。最长是一红一黑相间路径。
对于近似平衡来说:
①最优情况就是左右平衡,此时每条路径都是全黑或者是一红一黑相间,形成满二叉树。
②差的情况就是左右越不平衡,情况就越差。比如左子树全黑,而右子树是一黑一红相间。假设左子树全黑的路径长度位h = logN,因为红黑树要求每条路径的黑色节点的数量是相同的,而右子树是一红一黑相间的,那就说明右子树的长度是左子树的两倍h = 2*logN,这是最差的情况了,再差点就不是红黑树了。
红黑树节点的定义
红黑树节点的定义,跟AVL树的区别就是红黑树不需要平衡因子,而加入了颜色红跟黑。在定义当中,构造函数初始化列表对颜色_col默认初始化为红色是因为权衡了上面所述红黑树性质中的性质3和性质4。
性质3是说明了红黑树没有连续的红色节点,性质4说明的是每条路径都有相同数量的黑色节点。我们在定义节点的时候,需要给节点的颜色初始化,要么是红色,要么是黑色。
如果我们选择了黑色,那么在插入新节点之前,我们是往红黑树插入的嘛,本身就是红黑树,再插入一个黑色节点的话,那么必定会破坏掉红黑树的规则,是一定被破坏掉的,那么就一定需要对这颗红黑树进行调整。
如果我们选择红色,那么有可能会破坏掉红黑树的规则,也可能不会造成破坏。因为新增的节点的父节点是黑色的,那么就不会造成影响,而父节点是红色的话,那就需要调整。
因此,综上所述,默认初始化为红色是比较好的选择。
//使用枚举
enum Colour
{RED,BLACK,
};template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr) //跟AVL树一样,使用parent节点是为了旋转,_col(RED) //默认是红色{}
};红黑色的插入操作
红黑树是在二叉搜索树的基础上加入了平衡限制条件的树,因此红黑树的插入分为两步:
第一步:按照二叉搜索树的规则插入新节点。
第二步:检测新节点插入后,红黑树的性质是否造到破坏。
判断依据:因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
本文约定好:cur为当前节点,p(parent)为父节点,g(grandther)为祖父节点,u(uncle)为叔叔节点。
①cur为红,p为红,g为黑,u存在且为红
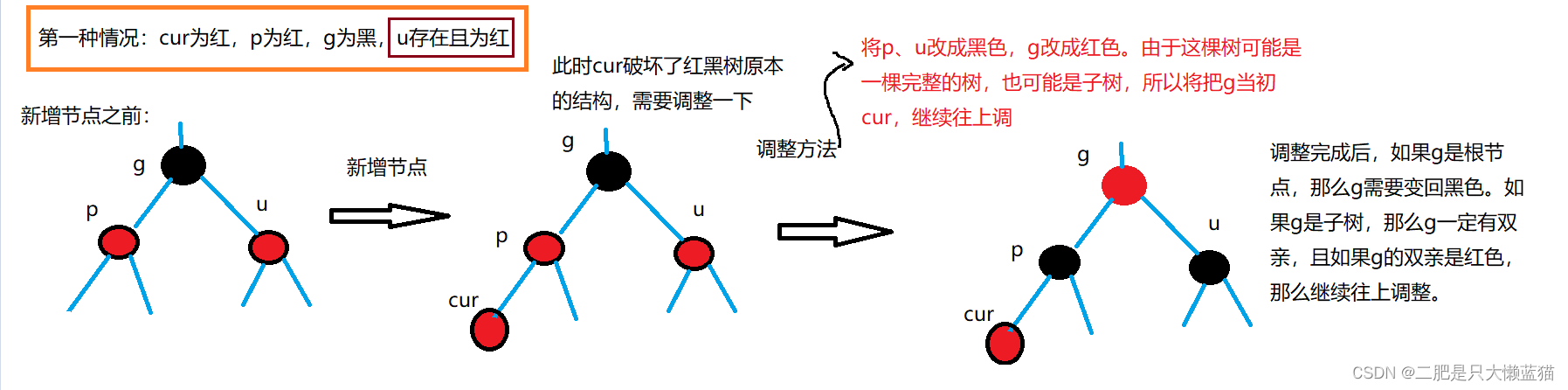
这种情况是插入的节点cur是红色的(默认),cur的双亲节点和叔叔节点是红色的,祖先节点是黑色的。因为不能连续存在红色节点,那么就需要把颜色调整一下即可,不需要旋转。
调整的方法为:将p节点和u节点的颜色改成黑色,同时为了防止g不是一棵单独的树,先把它变成红色,再进行判断,如果是单独的树,那么就把g的颜色变回黑色,如果是一棵子树,那么就往上继续调整。
②cur为红,p为红,g为黑,u不存在/u存在且为黑
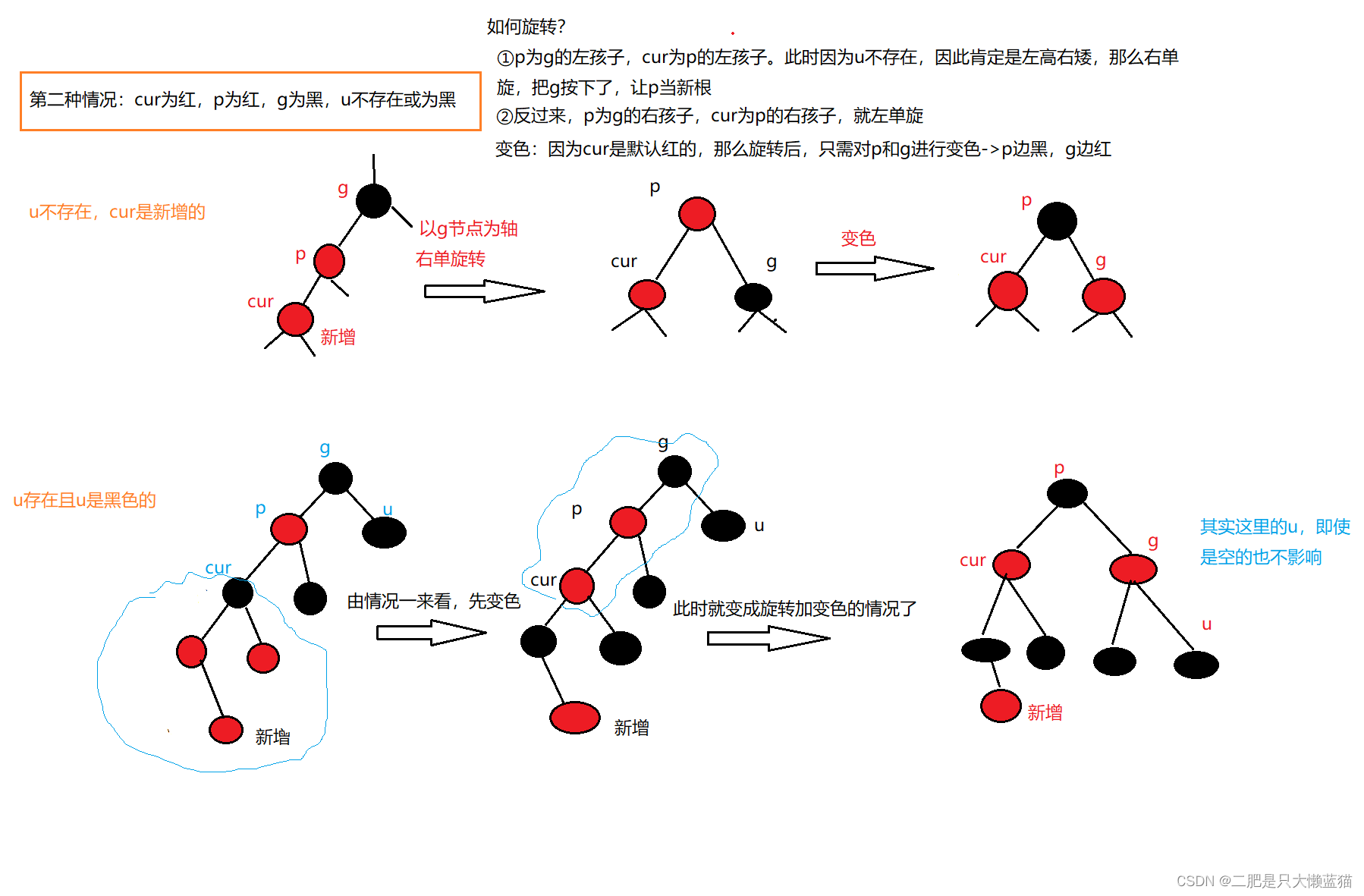
这种情况下是需要旋转+变色的。因为当cur为红色,p为红色,g为黑色,而u的情况是:
如果u不存在,cur肯定是新增的节点,因为在新增之前,p和g组成的树是一棵红黑树,在cur新增之后,不符合红黑树的性质。
这种情况下光凭变色是解决不了问题的,因为u为空说明有一条路径只有根节点,而另一条路径上会存在连续红,只凭变色,无论怎么变,都会导致各路径的黑色节点数量不相同,所以需要先根据p和cur的位置来决定旋转的方向而旋转,再变色。
如果u存在,则u是黑色,并且cur原本的颜色一定是黑色的,而现在cur的颜色是红色,那就肯定是第一种情况调整后,导致了现在的cur的颜色变了。
这种情况下就跟u不存在的情况一样,采用旋转+变色来解决问题。此时,u存在不存在已经没什么关系了(单独是看构造红黑树的情况来说)。
③cur为红,p为红,g为黑,u不存在/u存在且为黑
这种情况的颜色是跟情况二的一样,区别就是节点的位置不一样。
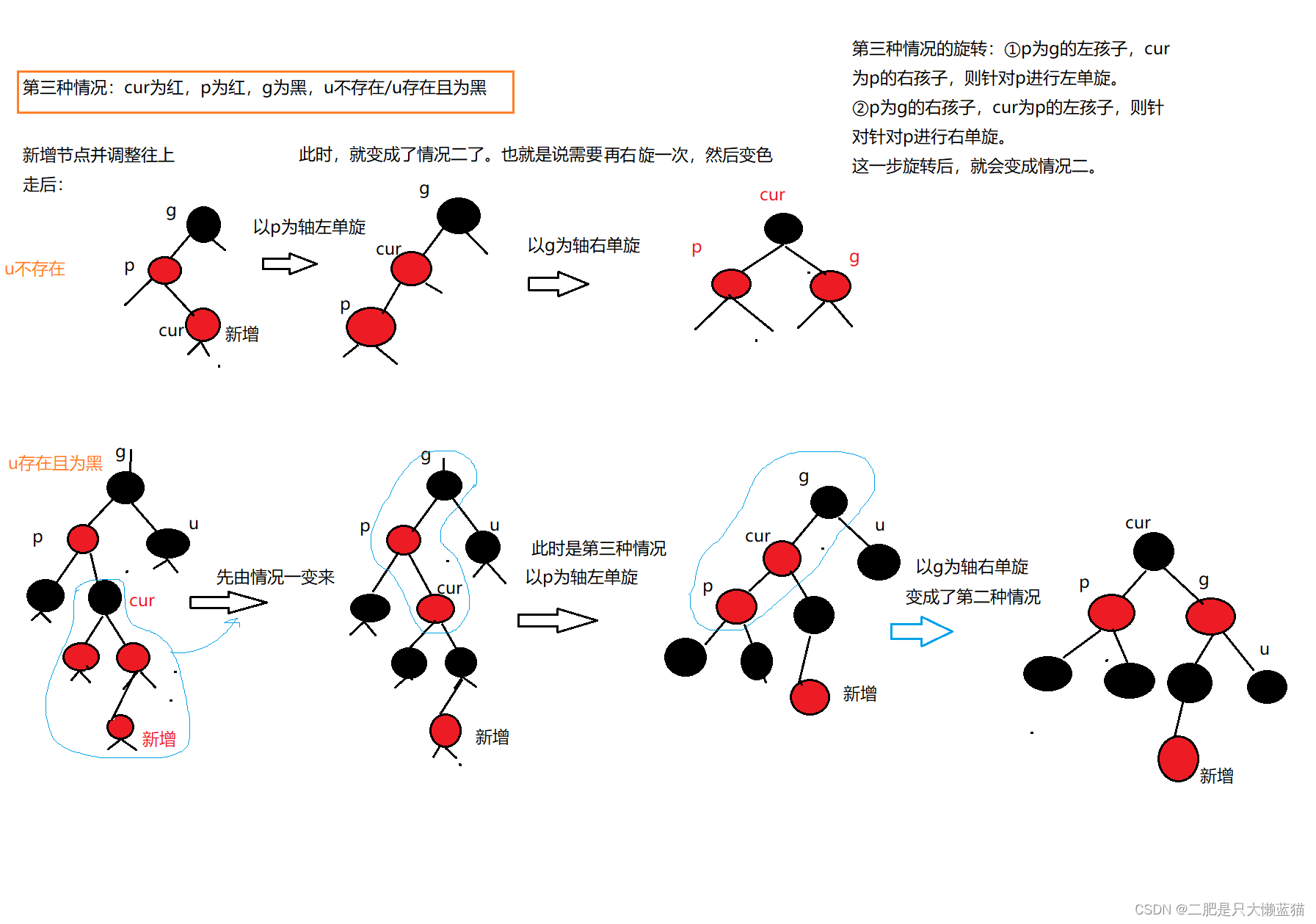
这种情况是跟第二中情况差不多,就是多了一步旋转,先左旋再右旋,或者先右旋再左旋。
整体代码如下:
template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){//先按二叉搜索树的规矩来创建一棵二叉搜索树if (_root==nullptr){_root = new Node(kv);//因为红黑树的根节点是黑色的_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;//多写一步,防止写错代码。if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//创建完二叉搜索树//开始创建红黑树,使用颜色来判断是否需要调整//循环往上走,循环条件:当走到的parent不为空,并且parent是红色的//即我们列举是三种情况,parent都是红的,就需要重新调整//如果parent是黑色的,那就不需要了。直接就是一棵红黑树,不进入循环while (parent && parent->_col == RED){//保存祖先节点,即g节点Node* grandfther = parent->_parent;//判断父节点是在祖先节点的哪边if (parent == grandfther->_left){//父节点在左边,那么叔叔节点就在右边Node* uncle = grandfther->_right;//情况一:uncle存在且为红。改变颜色即可if (uncle && uncle->_col == RED){//变色。parent->_col = uncle->_col = BLACK;grandfther->_col = RED;//往上走cur = grandfther;parent = cur->_parent;}else //uncle不存在 或者 存在但是黑色{//情况二 p是g的左孩子,cur是p的左孩子,以g为轴右单旋if (cur == parent->_left){//右单旋RotateR(grandfther);//变色 右单旋后,parent为根节点,变黑色。cur和g节点为红色parent->_col = BLACK;grandfther->_col = RED;}else //情况三 p是g的左孩子,cur是p的右孩子.{//先以p为轴左旋转RotateL(parent);//变成情况二,再以g为轴右单旋RotateR(grandfther);//变色 cur变成根节点,为黑色。p和g是红色cur->_col = BLACK;grandfther->_col = RED;}break;}}else //parent是在grandfther的右边{//叔叔节点就在祖先节点的左边Node* uncle = grandfther->_left;//情况一:uncle存在且为红。改变颜色即可if (uncle && uncle->_col == RED){//变色。parent->_col = uncle->_col = BLACK;grandfther->_col = RED;//往上走cur = grandfther;parent = cur->_parent;}else //uncle不存在 或者 存在但是黑色{//情况二 p是g的右孩子,cur是p的右孩子。if (cur == parent->_right){//左单旋RotateL(grandfther);//变色 右单旋后,parent为根节点,变黑色。cur和g节点为红色parent->_col = BLACK;grandfther->_col = RED;}else //情况三 p是g的右孩子,cur是p的左孩子.{//先以p为轴右旋转RotateR(parent);//变成情况二,再以g为轴左单旋RotateL(grandfther);//变色 cur变成根节点,为黑色。p和g是红色cur->_col = BLACK;grandfther->_col = RED;}break;}}}//最后将根节点置为黑_root->_col = BLACK;return true;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else {if (ppNode->_left == parent) {ppNode->_left = subL;}else {ppNode->_right = subL;}subL->_parent = ppNode;}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left; parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left = parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}private:Node* _root = nullptr;
};旋转请看:AVL树这篇文章有详细解析。红黑树的旋转直接复用AVL树的旋转的代码即可。
红黑树与AVL树的对比
⭐相同点:红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log_2 N)。
⭐不同点:红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言降低了插入和旋转的次数。而AVL树是高度平衡的二叉搜索树,旋转的次数比红黑树的要频繁。
所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
也就是因为红黑树在修改操作方面的性能比AVL树好,因此红黑树都用在了C++的STL库(map/set、mutil_map/mutil_set),Java库、Linux内核等等地方。
相关文章:

C++:红黑树
红黑树的概念 红黑树是一棵二叉搜索树,但是红黑树通过增加一个存储位表示结点的颜色RED或BLACK。通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出2倍,因而是接近平衡的。 红黑树的性质 ⭐…...

每天一道算法题の中缀表达式
中缀表达式(、-、*、/) :中缀表达式是指操作符位于操作数之间的数学表达式。例如,在中缀表达式"2 3"中,操作符""位于操作数"2"和"3"之间。现给定一个中缀表达式,…...

Dar语法基础-泛型
泛型 如果查看基本数组类型 List 的 API 文档,您会发现该类型实际上是 List<E>。 <…> 表示法将 List 标记为泛型(或参数化)类型——具有正式类型参数的类型。 按照惯例,大多数类型变量的名称都是单字母的࿰…...
配置)
rt-thread------串口(一)配置
系列文章目录 rt-thread 之 fal移植 rt-thread 之 生成工程模板 文章目录系列文章目录前言一、串口的配置step1:通过串口名字找到串口句柄step2:配置串口参数step3:设置串口接收回调函数step4:打开串口设备前言 UART(…...
Android - 自动系统签名
一、系统签名 以下是两类应用开发场景: 普通应用开发:使用公司自定义 keystore 进行签名,如:微信、支付宝系统应用开发:使用 AOSP 系统签名或厂商自定义 keystore 进行签名,如:设置、录音 系…...
SSH 服务详解 (八)-- vscode 通过 SSH 远程连接 linux 服务器
vscode 通过 SSH 远程连接 linux 服务器 SSH服务详解(一)–Linux SSH 服务器与客户端的安装与启动 SSH服务详解(二)–使用私钥登录 SSH 服务器(免密登录) SSH 服务详解 (三)-- 使用 SSH 代理 SSH 服务详解 (四)-- 本地调用远程主机的命令 SSH 服务详解 (五)-- 远程文件拷贝…...
)
【PTA Advanced】1060 Are They Equal(C++)
目录 题目 Input Specification: Output Specification: Sample Input 1: Sample Output 1: Sample Input 2: Sample Output 2: 思路 C 知识点UP 代码 题目 If a machine can save only 3 significant digits, the float numbers 12300 and 12358.9 are considered …...
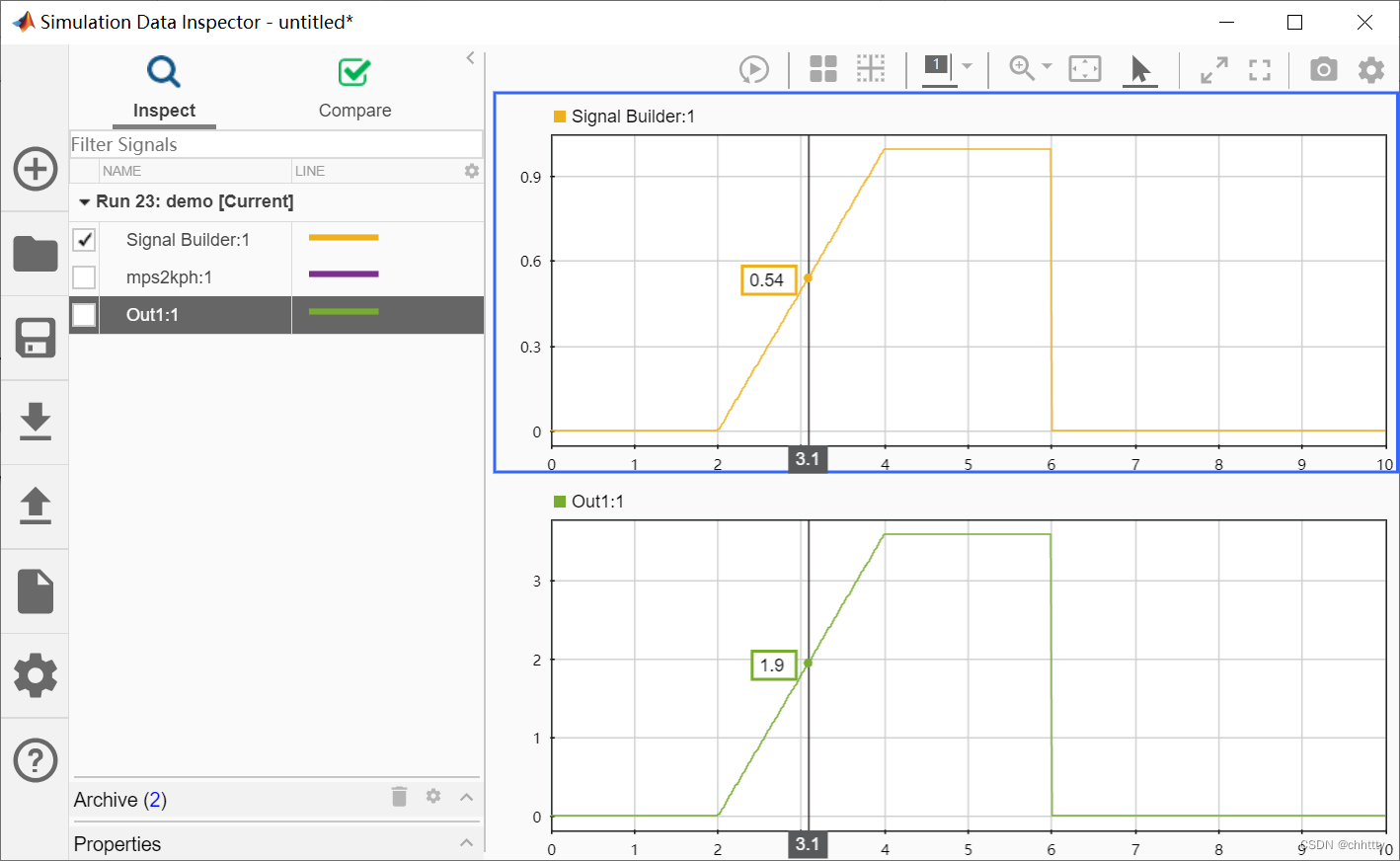
仿真与测试:通过Signal Builder模块生成输入信号
本文研究通过Signal Builder模块生成输入信号的方法。 文章目录1 生成输入信号2 仿真过程2.1 搭建被测模型2.2 搭建Signal Builder输入模块2.3 配置仿真log及仿真3 总结1 生成输入信号 在汽车的电控软件开发中,经常会在Simulink模型内部进行单元测试。单元测试的本…...

云计算培训靠谱吗?
怎么算靠谱的培训呢? 举个例子: 我想参加云计算培训找个工作,机构满足了我的要求,有工作了,但是不是做云计算相关的。 小强也参加了云计算培训,想学好云计算成为技术大牛,最后专业学得普普通…...

力扣SQL刷题10
目录标题618. 学生地理信息报告--完全不会的新题型1097. 游戏玩法分析 V - 重难点1127. 用户购买平台--难且不会618. 学生地理信息报告–完全不会的新题型 max()函数的功效:(‘jack’, null, null)中得出‘jack’,(nul…...

31 岁生日快乐,Linux!
Linux 迎来了 31 岁生日,所以和我一起庆祝 Linux 的 31 岁生日吧,喝上一杯好香槟和一个美味的蛋糕!虽然有些人不承认 8 月 25 日是 Linux 的生日,但我知道。1991 年 8 月 25 日,21 岁的芬兰学生 Linus Benedict Torval…...
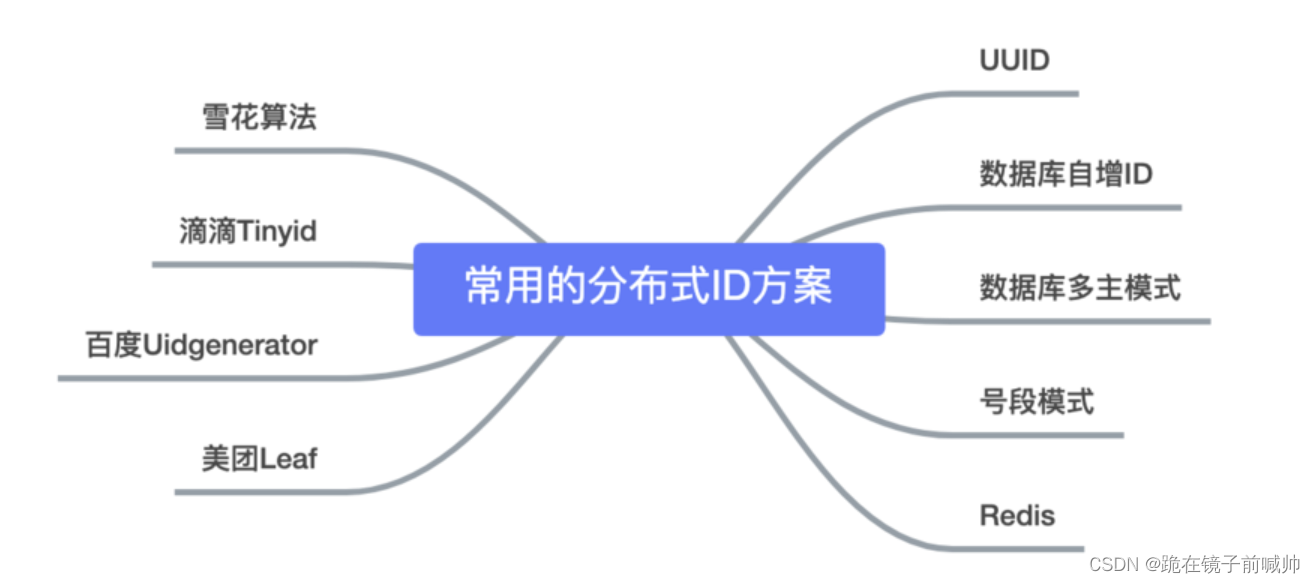
分布式ID生成方案
文章目录前言一、分布式ID需要满足的条件二、分布式ID生成方式基于UUID数据库自增数据库集群数据库号段模式redis ID生成基于雪花算法(Snowflake)模式百度(uid-generator)美团(Leaf)滴滴(Tinyid…...
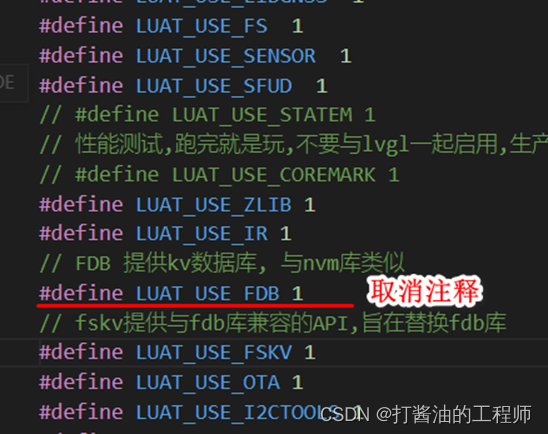
合宙Air103|fbd数据库| fskv - 替代fdb库|LuatOS-SOC接口|官方demo|学习(16):类redis的fbd数据库及fskv库
基础资料 基于Air103开发板:🚗 Air103 - LuatOS 文档 上手:开发上手 - LuatOS 文档 探讨重点 对官方社区库接口类redis的fbd数据库及fskv库的调用及示例进行复现及分析,了解两库的基本原理及操作方法。 软件及工具版本 Luat…...

【论文精读】Deep Residual Learning for Image Recognition
1 Degradation Problem💦 深度卷积神经网络在图像分类方面取得了一系列突破。深度网络自然地将低/中/高级特征和分类器以端到端的多层方式集成在一起,特征的“层次”可以通过堆叠层数(深度)来丰富。最近的研究揭示了网络深度是至关重要的,在具…...

Lesson2:基础语法、输出输入
一、基础语法 1、行结构 一个Python程序可分为许多逻辑行,一般来说:一个语句就是一行代码,不会跨越多行。 """比如下面的Python程序,一共有3个逻辑行,每一行都通过print()输出一个结果。""…...

android 9.0去掉前置摄像头闪光灯功能
1.1概述 在9.0的系统rom定制化开发中,在系统中camera2也是非常重要的一部分功能,在很多场合会用到camera2拍照视频,等等功能, 但是在使用过程中发现系统camera2在使用的时候,在前置摄像头进行拍照的时候,会出现闪光灯的情况,对于产品来说,者就是一个大问题,所以产品要求…...

静态分析工具Cppcheck在Windows上的使用
之前在https://blog.csdn.net/fengbingchun/article/details/8887843 介绍过Cppcheck,那时还是1.x版本,现在已到2.x版本,这里再总结下。 Cppcheck是一个用于C/C代码的静态分析工具,源码地址为https://github.com/danmar/cppcheck …...

用一年时间脱胎换骨
生活习惯篇早睡早起11点30之前必须睡觉按时吃饭特别是早餐控糖,少吃甜食早起刷牙后,喝一杯温水保持身材,养成运动健身的习惯养成持续写作的习惯记录选题,金句,素材断舍离,定期整理,把不用的东西…...

全景拼接python旗舰版
前言在这个项目中,您将构建一个管道,将几幅图像拼接成一个全景图。您还将捕获一组您自己的图像来报告最终的结果。步骤1 特征检测与描述本项目的第一步是对序列中的每幅图像分别进行特征检测。回想一下我们在这个类中介绍过的一些特征探测器:…...
常见的字符串与内存操作函数)
(C语言)常见的字符串与内存操作函数
问:1. Solve the problems:我想用三种方法求字符串的长度怎么办?2. strlen处理的字符串中有什么时需要注意:什么只记为什么?当什么不起什么作用时,什么不计算在内,编译器会把什么,什…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
