PyTorch的自动微分模块【含梯度基本数学原理详解】
文章目录
- 1、简介
- 1.1、基本概念
- 1.2、基本原理
- 1.2.1、自动微分
- 1.2.2、梯度
- 1.2.3、梯度求导
- 1.2.4、梯度下降法
- 1.2.5、张量梯度举例
- 1.3、Autograd的高级功能
- 2、梯度基本计算
- 2.1、单标量梯度
- 2.2、单向量梯度的计算
- 2.3、多标量梯度计算
- 2.4、多向量梯度计算
- 3、控制梯度计算
- 4、累计梯度
- 5、梯度下降优化最优解⭐
- 6、梯度计算注意事项
- 7、张量转标量的选择⭐
🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步涉猎人工智能和前端开发。
🦅个人主页:@逐梦苍穹
📕所属专栏:人工智能
🌻gitee地址:xzl的人工智能代码仓库
✈ 您的一键三连,是我创作的最大动力🌹
1、简介
本文目标:掌握梯度计算
先补充一篇我的文章,关于向量的计算方式:https://xzl-tech.blog.csdn.net/article/details/140563909
自动微分(Automatic Differentiation, Autograd)是计算梯度的强大工具,广泛应用于机器学习,特别是深度学习模型的训练过程中。
在PyTorch中,Autograd模块通过记录张量的操作并自动计算梯度,极大地简化了模型的优化过程。
1.1、基本概念
- 张量(Tensor):
- PyTorch中的张量是自动微分的基础数据结构。每个张量都有一个属性
requires_grad,它指示是否需要计算该张量的梯度。 - 张量的
grad属性用于存储计算得到的梯度。
- PyTorch中的张量是自动微分的基础数据结构。每个张量都有一个属性
- 计算图(Computational Graph):
- Autograd的核心是动态计算图,每次进行操作时都会动态地构建计算图。计算图的节点表示张量,边表示操作。
- 在反向传播过程中,Autograd沿着计算图从输出节点到输入节点计算梯度。
- 反向传播(Backpropagation):
- 反向传播是一种计算梯度的算法,通过链式法则(链式求导法则)逐层计算梯度。
自动微分(Autograd)模块对张量做了进一步的封装,具有自动求导功能。自动微分模块是构成神经网络训练的必要模块,在神经网络的反向传播过程中,Autograd 模块基于正向计算的结果对当前的参数进行微分计算,从而实现网络权重参数的更新。
1.2、基本原理
1.2.1、自动微分
在PyTorch中,自动微分通过记录对张量的所有操作来实现。当调用反向传播函数backward()时,Autograd根据链式法则自动计算所有梯度。
链式法则:
设 y = f ( u ) y = f(u) y=f(u) 且 u = g ( x ) u = g(x) u=g(x) ,根据链式法则,函数 ( y ) ( y ) (y)对 ( x ) ( x ) (x) 的导数为:
[ d y d x = d y d u ⋅ d u d x ] [ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} ] [dxdy=dudy⋅dxdu]
在计算图中,Autograd通过遍历所有节点,按此法则计算梯度。
1.2.2、梯度
梯度 (Gradient)
梯度是多变量函数的偏导数向量,它表示函数在各个变量方向上的变化率。
在数学上,给定一个多变量函数 ( f ( x 1 , x 2 , . . . , x n ) ) ( f(x_1, x_2, ..., x_n) ) (f(x1,x2,...,xn)),它的梯度是一个向量,
其分量是函数对每个变量的偏导数: [ ∇ f = ( ∂ f ∂ x 1 , ∂ f ∂ x 2 , . . . , ∂ f ∂ x n ) ] [ \nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n} \right) ] [∇f=(∂x1∂f,∂x2∂f,...,∂xn∂f)]
梯度向量指向函数值增长最快的方向,其长度表示函数值增长最快的速率。
1.2.3、梯度求导
梯度求导 (Gradient Calculation)
梯度求导是计算函数在特定点的梯度向量的过程。对于机器学习和深度学习中的目标函数(通常是损失函数),我们通过梯度求导来了解参数变化对目标函数的影响,从而调整参数以最小化目标函数。
一维函数的导数:
对于一维函数 ( f ( x ) ) ( f(x) ) (f(x)),导数 ( f ′ ( x ) ) ( f'(x) ) (f′(x))表示函数在点 ( x ) ( x ) (x)处的变化率。
数学上,导数定义为: [ f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x ] [ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} ] [f′(x)=limΔx→0Δxf(x+Δx)−f(x)]
多维函数的梯度:
对于多维函数 ( f ( x 1 , x 2 , . . . , x n ) ) ( f(x_1, x_2, ..., x_n) ) (f(x1,x2,...,xn)),梯度是各个方向上的导数组成的向量:
[ ∇ f = ( ∂ f ∂ x 1 , ∂ f ∂ x 2 , . . . , ∂ f ∂ x n ) ] [ \nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n} \right) ] [∇f=(∂x1∂f,∂x2∂f,...,∂xn∂f)]
1.2.4、梯度下降法
梯度下降法 (Gradient Descent)
梯度下降法是一种优化算法,通过逐次调整参数以最小化目标函数。具体步骤如下:
- 初始化参数 ( θ ) ( \theta ) (θ)。
- 计算当前参数的梯度 ( ∇ f ( θ ) ) ( \nabla f(\theta) ) (∇f(θ))。
- 更新参数: ( θ = θ − α ∇ f ( θ ) ) ( \theta = \theta - \alpha \nabla f(\theta) ) (θ=θ−α∇f(θ)),其中 ( α ) ( \alpha ) (α)是学习率。
- 重复步骤2和3,直到收敛。
1.2.5、张量梯度举例
标量对张量的梯度:
假设有一个标量函数 ( f ) ( f ) (f)作用于张量 ( T ) ( T ) (T),梯度 ( ∇ f ) ( \nabla f ) (∇f)是一个与 ( T ) ( T ) (T)具有相同维度的张量,
其元素是 ( f ) ( f ) (f)对 ( T ) ( T ) (T)中每个元素的偏导数: [ ( ∇ f ) i j k . . . = ∂ f ∂ T i j k . . . ] [ (\nabla f){ijk...} = \frac{\partial f}{\partial T{ijk...}} ] [(∇f)ijk...=∂Tijk...∂f]
例子:张量的平方和函数:
考虑一个张量的平方和函数: [ f ( T ) = ∑ i , j , k , . . . T i j k . . . 2 ] [ f(T) = \sum_{i,j,k,...} T_{ijk...}^2 ] [f(T)=∑i,j,k,...Tijk...2]
对张量 ( T ) 的每个元素求导: [ ∂ f ∂ T i j k . . . = 2 T i j k . . . ] [ \frac{\partial f}{\partial T_{ijk...}} = 2T_{ijk...} ] [∂Tijk...∂f=2Tijk...]
所以,梯度是: [ ∇ f = 2 T ] [ \nabla f = 2T ] [∇f=2T]
在实际应用中,通常需要对更复杂的函数计算梯度,如神经网络的损失函数对模型参数的梯度。这时,梯度计算不仅限于简单的平方和函数,而是涉及到复杂的链式求导。
例子:神经网络的反向传播
考虑一个简单的神经网络前向传播: [ y = σ ( W x + b ) ] [ y = \sigma(Wx + b) ] [y=σ(Wx+b)]
其中 ( σ ) ( \sigma ) (σ)是激活函数, ( W ) ( W ) (W) 是权重矩阵, ( x ) ( x ) (x) 是输入, ( b ) ( b ) (b)是偏置。
假设损失函数是均方误差: [ L = 1 2 ( y − y ^ ) 2 ] [ L = \frac{1}{2}(y - \hat{y})^2 ] [L=21(y−y^)2]
我们需要计算损失函数对权重矩阵和偏置的梯度。
1.3、Autograd的高级功能
- 梯度累积:
- 默认情况下,调用
backward()时,梯度会累积到张量的grad属性中。可以通过x.grad.zero_()来清零梯度。
- 默认情况下,调用
- 非标量输出的梯度:
- 当输出不是标量时,可以传递一个和输出形状相同的权重张量作为
backward()的参数,用于计算加权和的梯度。
- 当输出不是标量时,可以传递一个和输出形状相同的权重张量作为
- 禁用梯度计算:
- 在不需要梯度计算的情况下,可以使用
torch.no_grad()或with torch.no_grad():来临时禁用梯度计算,从而提高性能和节省内存。
- 在不需要梯度计算的情况下,可以使用
我们使用 backward 方法、grad 属性来实现梯度的计算和访问.
2、梯度基本计算
2.1、单标量梯度
import torch
# 1. 单标量梯度的计算
# y = x**2 + 20
def test01():# 定义需要求导的张量# 张量的值类型必须是浮点类型x = torch.tensor(10, requires_grad=True, dtype=torch.float64)print(x)# 变量经过中间运算f = x ** 2 + 20print(f)# 自动微分f.backward()# 打印 x 变量的梯度# backward 函数计算的梯度值会存储在张量的 grad 变量中print(x.grad)print(x)
程序运行结果:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\1-梯度基本计算.py
tensor(10., dtype=torch.float64, requires_grad=True)
tensor(120., dtype=torch.float64, grad_fn=<AddBackward0>)
tensor(20., dtype=torch.float64)
tensor(10., dtype=torch.float64, requires_grad=True)Process finished with exit code 0
解释:
- 张量
x的初始值:tensor(10., dtype=torch.float64, requires_grad=True)表示x的初始值是10,并且它的梯度计算已被启用。- 中间变量
f的值:tensor(120., dtype=torch.float64, grad_fn=<AddBackward0>)表示f的计算结果是120,即 ( 1 0 2 + 20 ) (10^2 + 20) (102+20)。- 梯度值
x.grad:tensor(20., dtype=torch.float64)表示f对x的梯度是20,即 d d x ( x 2 + 20 ) = 2 x = 2 × 10 \frac{d}{dx}(x^2 + 20) = 2x = 2 \times 10 dxd(x2+20)=2x=2×10。- 张量
x的值保持不变:tensor(10., dtype=torch.float64, requires_grad=True)再次确认x的值保持为10。
2.2、单向量梯度的计算
# 2. 单向量梯度的计算
# y = x**2 + 20
def test02():# 定义需要求导张量x = torch.tensor([10, 20, 30, 40], requires_grad=True, dtype=torch.float64)print(x)# 变量经过中间计算f1 = x ** 2 + 20print(f1)# 注意:# 由于求导的结果必须是标量# 而 f 的结果是: tensor([120., 420.])# 所以, 不能直接自动微分# 需要将结果计算为标量才能进行计算print(f1.mean())f2 = f1.mean() # f2 = 1/2 * x# 自动微分f2.backward()# 打印 x 变量的梯度print(x.grad)
输出:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\1-梯度基本计算.py
tensor([10., 20., 30., 40.], dtype=torch.float64, requires_grad=True)
tensor([ 120., 420., 920., 1620.], dtype=torch.float64,grad_fn=<AddBackward0>)
tensor(770., dtype=torch.float64, grad_fn=<MeanBackward0>)
tensor([ 5., 10., 15., 20.], dtype=torch.float64)Process finished with exit code 0
解释:
函数
f1的定义: [ f 1 i = x i 2 + 20 ] [ f_{1i} = x_i^2 + 20 ] [f1i=xi2+20]
f2是f1的均值: [ f 2 = 1 4 ∑ i = 1 4 f 1 i ] [ f2 = \frac{1}{4} \sum_{i=1}^4 f_{1i} ] [f2=41∑i=14f1i]
因此,f2对x_i的偏导数为: [ ∂ f 2 ∂ x i = 1 4 ∂ f 1 i ∂ x i = 1 4 ⋅ 2 x i = 1 2 x i ] [ \frac{\partial f2}{\partial x_i} = \frac{1}{4} \frac{\partial f_{1i}}{\partial x_i} = \frac{1}{4} \cdot 2x_i = \frac{1}{2} x_i ] [∂xi∂f2=41∂xi∂f1i=41⋅2xi=21xi]
所以,f2对x的梯度x.grad为每个元素的一半: [ x . g r a d = [ 1 2 ⋅ 10 , 1 2 ⋅ 20 , 1 2 ⋅ 30 , 1 2 ⋅ 40 ] = [ 5 , 10 , 15 , 20 ] ] [ x.grad = \left[ \frac{1}{2} \cdot 10, \frac{1}{2} \cdot 20, \frac{1}{2} \cdot 30, \frac{1}{2} \cdot 40 \right] = [5, 10, 15, 20] ] [x.grad=[21⋅10,21⋅20,21⋅30,21⋅40]=[5,10,15,20]]
2.3、多标量梯度计算
# 3. 多标量梯度计算
# y = x1 ** 2 + x2 ** 2 + x1*x2
def test03():# 定义需要计算梯度的张量x1 = torch.tensor(10, requires_grad=True, dtype=torch.float64)x2 = torch.tensor(20, requires_grad=True, dtype=torch.float64)print(x1, x2)# 经过中间的计算y = x1 ** 2 + x2 ** 2 + x1 * x2print(y)# TODO y已经是标量, 无需转换# 自动微分y.backward()# 打印两个变量的梯度print(x1.grad, x2.grad)
输出:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\1-梯度基本计算.py
tensor(10., dtype=torch.float64, requires_grad=True) tensor(20., dtype=torch.float64, requires_grad=True)
tensor(700., dtype=torch.float64, grad_fn=<AddBackward0>)
tensor(40., dtype=torch.float64) tensor(50., dtype=torch.float64)Process finished with exit code 0
解释-梯度计算细节:
定义函数( y ) ( y ) (y): [ y = x 1 2 + x 2 2 + x 1 ⋅ x 2 ] [ y = x_1^2 + x_2^2 + x1 \cdot x2 ] [y=x12+x22+x1⋅x2]计算( y ) ( y ) (y): [ y = 102 + 202 + 10 ⋅ 20 = 100 + 400 + 200 = 700 ] [ y = 102 + 202 + 10 \cdot 20 = 100 + 400 + 200 = 700 ] [y=102+202+10⋅20=100+400+200=700]- 计算梯度 ( ∂ y ∂ x 1 \frac{\partial y}{\partial x1} ∂x1∂y): [ ∂ y ∂ x 1 = 2 x 1 + x 2 = 2 ⋅ 10 + 20 = 20 + 20 = 40 ] [ \frac{\partial y}{\partial x1} = 2x1 + x2 = 2 \cdot 10 + 20 = 20 + 20 = 40 ] [∂x1∂y=2x1+x2=2⋅10+20=20+20=40]
- 计算梯度 ( ∂ y ∂ x 2 \frac{\partial y}{\partial x2} ∂x2∂y): [ ∂ y ∂ x 2 = 2 x 2 + x 1 = 2 ⋅ 20 + 10 = 40 + 10 = 50 ] [ \frac{\partial y}{\partial x2} = 2x2 + x1 = 2 \cdot 20 + 10 = 40 + 10 = 50 ] [∂x2∂y=2x2+x1=2⋅20+10=40+10=50]
2.4、多向量梯度计算
# 4. 多向量梯度计算
def test04():# 定义需要计算梯度的张量x1 = torch.tensor([10, 20], requires_grad=True, dtype=torch.float64, device='cuda')x2 = torch.tensor([30, 40], requires_grad=True, dtype=torch.float64, device='cuda')# 经过中间的计算y = x1 ** 2 + x2 ** 2 + x1 * x2print(y)# 将输出结果变为标量y = y.mean()print(y)# 自动微分y.backward()# 打印两个变量的梯度print(x1.grad, x2.grad)
输出:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\1-梯度基本计算.py
tensor([1300., 2800.], device='cuda:0', dtype=torch.float64,grad_fn=<AddBackward0>)
tensor(2050., device='cuda:0', dtype=torch.float64, grad_fn=<MeanBackward0>)
tensor([25., 40.], device='cuda:0', dtype=torch.float64) tensor([35., 50.], device='cuda:0', dtype=torch.float64)Process finished with exit code 0
梯度计算细节:
- 定义函数 ( y ) ( y ) (y): [ y = x 1 2 + x 2 2 + x 1 ⋅ x 2 ] [ y = x_1^2 + x_2^2 + x_1 \cdot x_2 ] [y=x12+x22+x1⋅x2]
具体计算每个元素:
- 第一个元素: ( 1 0 2 + 3 0 2 + 10 ⋅ 30 = 100 + 900 + 300 = 1300 ) ( 10^2 + 30^2 + 10 \cdot 30 = 100 + 900 + 300 = 1300 ) (102+302+10⋅30=100+900+300=1300)
- 第二个元素: ( 2 0 2 + 4 0 2 + 20 ⋅ 40 = 400 + 1600 + 800 = 2800 ) ( 20^2 + 40^2 + 20 \cdot 40 = 400 + 1600 + 800 = 2800 ) (202+402+20⋅40=400+1600+800=2800)
所以 ( y = [ 1300 , 2800 ] ) ( y = [1300, 2800] ) (y=[1300,2800])
- 将结果转换为标量: [ y mean = 1 2 ∑ y = 1 2 ( 1300 + 2800 ) = 4100 2 = 2050 ] [ y_{\text{mean}} = \frac{1}{2} \sum y = \frac{1}{2} (1300 + 2800) = \frac{4100}{2} = 2050 ] [ymean=21∑y=21(1300+2800)=24100=2050]
- 计算梯度:
对( x 1 ) ( x_1 ) (x1)的梯度: [ ∂ y mean ∂ x 1 = 1 2 ( 2 x 1 + x 2 ) ] [ \frac{\partial y_{\text{mean}}}{\partial x_1} = \frac{1}{2} \left( 2x_1 + x_2 \right) ] [∂x1∂ymean=21(2x1+x2)]- 对第一个元素: ( 1 2 ( 2 ⋅ 10 + 30 ) = 1 2 ( 20 + 30 ) = 50 2 = 25 ) ( \frac{1}{2} (2 \cdot 10 + 30) = \frac{1}{2} (20 + 30) = \frac{50}{2} = 25 ) (21(2⋅10+30)=21(20+30)=250=25)
- 对第二个元素: ( 1 2 ( 2 ⋅ 20 + 40 ) = 1 2 ( 40 + 40 ) = 80 2 = 40 ) ( \frac{1}{2} (2 \cdot 20 + 40) = \frac{1}{2} (40 + 40) = \frac{80}{2} = 40 ) (21(2⋅20+40)=21(40+40)=280=40)
所以 ( x 1. g r a d = [ 25 , 40 ] ) ( x1.grad = [25, 40] ) (x1.grad=[25,40])
对( x 2 ) ( x_2 ) (x2)的梯度: [ ∂ y mean ∂ x 2 = 1 2 ( 2 x 2 + x 1 ) ] [ \frac{\partial y_{\text{mean}}}{\partial x_2} = \frac{1}{2} \left( 2x_2 + x_1 \right) ] [∂x2∂ymean=21(2x2+x1)]- 对第一个元素: ( 1 2 ( 2 ⋅ 30 + 10 ) = 1 2 ( 60 + 10 ) = 70 2 = 35 ) ( \frac{1}{2} (2 \cdot 30 + 10) = \frac{1}{2} (60 + 10) = \frac{70}{2} = 35 ) (21(2⋅30+10)=21(60+10)=270=35)
- 对第二个元素: ( 1 2 ( 2 ⋅ 40 + 20 ) = 1 2 ( 80 + 20 ) = 100 2 = 50 ) ( \frac{1}{2} (2 \cdot 40 + 20) = \frac{1}{2} (80 + 20) = \frac{100}{2} = 50 ) (21(2⋅40+20)=21(80+20)=2100=50)
**所以 ** ( x 2. g r a d = [ 35 , 50 ] ) ( x2.grad = [35, 50] ) (x2.grad=[35,50])
3、控制梯度计算
我们可以通过一些方法使得在 requires_grad=True 的张量在某些时候计算不进行梯度计算。
PyTorch 提供了几种方法来实现这一点,包括上下文管理器、装饰器和全局设置。
- 使用上下文管理器
torch.no_grad()- 使用装饰器
torch.no_grad()- 使用全局设置
torch.set_grad_enabled(False)
# 1. 控制不计算梯度
def test01():x = torch.tensor(10, requires_grad=True, dtype=torch.float64)print(x.requires_grad)# 第一种方式: 对代码进行装饰with torch.no_grad():y = x ** 2print(y.requires_grad)# 第二种方式: 对函数进行装饰@torch.no_grad()def my_func(x):return x ** 2print(my_func(x).requires_grad)# 第三种方式torch.set_grad_enabled(False)y = x ** 2print(y.requires_grad)
程序运行结果:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\2-控制梯度计算.py
True
False
False
FalseProcess finished with exit code 0
4、累计梯度
累计梯度:每一次训练前,都需要清楚现有梯度,如果不清楚,则会累加。
# 2. 注意: 累计梯度
def test02():# 定义需要求导张量x = torch.tensor([10, 20, 30, 40], requires_grad=True, dtype=torch.float64)for _ in range(3):f1 = x ** 2 + 20f2 = f1.mean()# 默认张量的 grad 属性会累计历史梯度值# 所以, 需要我们每次手动清理上次的梯度# 注意: 一开始梯度不存在, 需要做判断if x.grad is not None:x.grad.data.zero_()f2.backward()print(x.grad)
输出:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\2-控制梯度计算.py
tensor([ 5., 10., 15., 20.], dtype=torch.float64)
tensor([ 5., 10., 15., 20.], dtype=torch.float64)
tensor([ 5., 10., 15., 20.], dtype=torch.float64)Process finished with exit code 0
如果不清除,梯度值则累加:
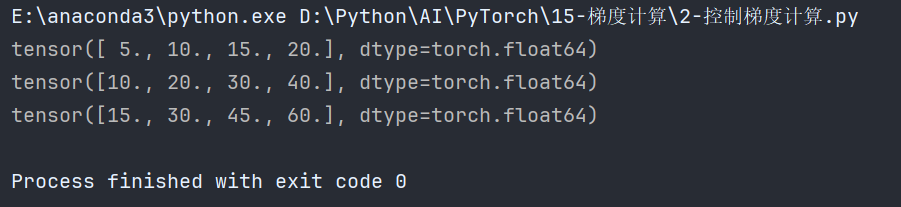
5、梯度下降优化最优解⭐
原理:
梯度下降法是一种优化算法,旨在通过反复调整参数,使目标函数的值达到最小
梯度下降的更新公式为: [ x new = x old − η ⋅ d d x ] [ x_{\text{new}} = x_{\text{old}} - \eta \cdot \frac{d}{dx} ] [xnew=xold−η⋅dxd]
- x new x_{\text{new}} xnew:更新后的参数值。
- x old x_{\text{old}} xold:当前的参数值。
- η \eta η:学习率,表示每次更新的步幅的大小。
- d d x \frac{d}{dx} dxd:目标函数 ( f ) ( f ) (f) 对参数 ( x ) ( x ) (x) 的梯度,表示 ( x ) ( x ) (x)方向上的变化率。
代码:
# 3. 梯度下降优化最优解
def test03():# y = x**2x = torch.tensor(10, requires_grad=True, dtype=torch.float64)for _ in range(5000):# 正向计算f = x ** 2# 梯度清零if x.grad is not None:x.grad.data.zero_()# 反向传播计算梯度f.backward()# 更新参数x.data = x.data - 0.001 * x.gradprint('%.10f' % x.data)
结果:
- 第一个结果是:9.9800000000
- 最后一个结果:0.0004494759
数学解释:
- 初始化参数 ( x ) ( x ) (x): [ x = 10 ] [ x = 10 ] [x=10]
- 目标函数 ( f ) ( f ) (f): [ f ( x ) = x 2 ] [ f(x) = x^2 ] [f(x)=x2]
- 计算梯度: [ d ( f ) d ( x ) = 2 x ] [ \frac{d(f)}{d(x)} = 2x ] [d(x)d(f)=2x]对于初始 ( x = 10 ) ( x = 10 ) (x=10),梯度为 ( 2 × 10 = 20 ) ( 2 \times 10 = 20 ) (2×10=20)。
- 更新参数: [ x new = x old − 0.001 ⋅ d ( f ) d ( x ) ] [ x_{\text{new}} = x_{\text{old}} - 0.001 \cdot \frac{d(f)}{d(x)} ] [xnew=xold−0.001⋅d(x)d(f)]对于初始 ( x = 10 ) ( x = 10 ) (x=10),更新后的 ( x ) 为: [ x new = 10 − 0.001 × 20 = 10 − 0.02 = 9.98 ] [ x_{\text{new}} = 10 - 0.001 \times 20 = 10 - 0.02 = 9.98 ] [xnew=10−0.001×20=10−0.02=9.98]
重复更新:
这个过程会在循环中重复多次,每次都根据新的 𝑥x 值计算梯度并更新参数。随着迭代次数的增加,𝑥x 会逐渐减小,最终趋近于 0,这是因为对于函数 𝑓(𝑥)=𝑥2f(x)=x2 而言,最小值在 𝑥=0x=0 处取得。
为什么选择梯度的负方向:
选择梯度的负方向是因为梯度表示函数值增加最快的方向。为了最小化函数,我们需要沿着梯度的反方向移动,即梯度的负方向。
学习率的选择:
学习率 η η η 决定了每次参数更新的步幅大小。选择合适的学习率非常重要:
- 学习率太大:会导致更新步幅过大,可能会跳过最优解,导致发散。
- 学习率太小:会导致更新步幅过小,收敛速度过慢,可能需要更多的迭代次数才能接近最优解。
总结:
梯度下降法是通过反复调整参数,使目标函数的值达到最小的一种优化算法。每次更新参数时,沿着梯度的负方向移动一个步幅,这个步幅由学习率决定。通过这种方式,逐步逼近目标函数的最优解。在实际应用中,选择合适的学习率和迭代次数,对于模型的优化效果至关重要。
6、梯度计算注意事项
当对设置 requires_grad=True 的张量使用 numpy 函数进行转换时, 会出现如下报错:
Can’t call numpy() on Tensor that requires grad. Use tensor.detach().numpy() instead.
此时, 需要先使用 detach 函数将张量进行分离, 再使用 numpy 函数.
注意:detach 之后会产生一个新的张量, 新的张量作为叶子结点,并且该张量和原来的张量共享数据, 但是分离后的张量不需要计算梯度。
# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/20 3:22
import torch# 1. detach 函数用法
def test01():x = torch.tensor([10, 20], requires_grad=True, dtype=torch.float64)# Can't call numpy() on Tensor that requires grad. Use tensor.detach().numpy() instead.# print(x.numpy()) # 错误print(x.detach().numpy()) # 正确# 2. detach 前后张量共享内存
def test02():x1 = torch.tensor([10, 20], requires_grad=True, dtype=torch.float64)# x2 作为叶子结点x2 = x1.detach()print(x1)print(x2)# 两个张量的值一样# TODO id() 函数用于返回对象的唯一标识符(identity)print(id(x1.data), id(x2.data))x2.data = torch.tensor([100, 200])print(x1)print(x2)# x2 不会自动计算梯度: Falseprint(x2.requires_grad)if __name__ == '__main__':print("test01")test01()print("test02")test02()
程序运行结果:
E:\anaconda3\python.exe D:\Python\AI\PyTorch\15-梯度计算\3-detach.py
test01
[10. 20.]
test02
tensor([10., 20.], dtype=torch.float64, requires_grad=True)
tensor([10., 20.], dtype=torch.float64)
3035001264464 3035001264464
tensor([10., 20.], dtype=torch.float64, requires_grad=True)
tensor([100, 200])
FalseProcess finished with exit code 0
不会自动计算梯度:

7、张量转标量的选择⭐
在机器学习和深度学习中,梯度的计算和应用是优化模型的核心部分。
- 梯度的作用
梯度是指函数在某一点的导数或变化率,表示该点处函数值变化最迅速的方向。
在深度学习中,梯度主要用于以下方面:
①优化模型参数:通过梯度下降法(或其变体),调整模型参数以最小化损失函数。
②反向传播:在训练神经网络时,通过计算损失函数相对于模型参数的梯度,更新参数,使得模型的预测更准确。
- 为什么梯度的值可以不一样
梯度的值取决于你选择的损失函数和如何将多维输出转换为标量。
例如,求和和求均值两种方法在将向量转换为标量时会导致不同的梯度值。
- 均值和求和得到的梯度在作用上的区别
求和:
梯度值较大:每个元素的梯度直接反映其对总和的贡献。适用于所有元素的贡献需要累加的情况。
更新步幅更大:在梯度下降中,更新步幅较大,因为梯度值较大。
求均值:
梯度值较小:每个元素的梯度反映其对均值的贡献。适用于考虑整体均衡贡献的情况。
更新步幅较小:在梯度下降中,更新步幅较小,因为梯度值较小。
总结:
- 梯度的作用:梯度用于优化模型参数,使得损失函数最小化。
- 梯度的值可以不一样:不同的标量化方法(如求和和求均值)会导致不同的梯度值。
- 求和与求均值的区别:求和使梯度较大,更新步幅较大;求均值使梯度较小,更新步幅较小。选择哪种方法取决于具体应用和需求。
相关文章:

PyTorch的自动微分模块【含梯度基本数学原理详解】
文章目录 1、简介1.1、基本概念1.2、基本原理1.2.1、自动微分1.2.2、梯度1.2.3、梯度求导1.2.4、梯度下降法1.2.5、张量梯度举例 1.3、Autograd的高级功能 2、梯度基本计算2.1、单标量梯度2.2、单向量梯度的计算2.3、多标量梯度计算2.4、多向量梯度计算 3、控制梯度计算4、累计…...

AI 绘画|Midjourney设计Logo提示词
你是否已经看过许多别人分享的 MJ 咒语,却仍无法按照自己的想法画图?通过学习 MJ 的提示词逻辑后,你将能够更好地理解并创作自己的“咒语”。本文将详细拆解使用 MJ 设计 Logo 的逻辑,让你在阅读后即可轻松上手,制作出…...

LeNet实验 四分类 与 四分类变为多个二分类
目录 1. 划分二分类 2. 训练独立的二分类模型 3. 二分类预测结果代码 4. 二分类预测结果 5 改进训练模型 6 优化后 预测结果代码 7 优化后预测结果 8 训练四分类模型 9 预测结果代码 10 四分类结果识别 1. 划分二分类 可以根据不同的类别进行多个划分,以…...

【BUG】已解决:java.lang.reflect.InvocationTargetException
已解决:java.lang.reflect.InvocationTargetException 欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 欢迎来到我的主页,我是博主英杰,211科班出身,就职于医疗科技公司,热衷分享知识,武汉城市开发…...

配置kali 的apt命令在线安装包的源为国内源
目录 一、安装VMware Tools 二、配置apt国内源 一、安装VMware Tools 点击安装 VMware Tools 后,会加载一个虚拟光驱,里面包含 VMware Tools 的安装包 鼠标右键单击 VMware Tools 的安装包,点击复制到 点击 主目录,再点击选择…...

JAVA 异步编程(线程安全)二
1、线程安全 线程安全是指你的代码所在的进程中有多个线程同时运行,而这些线程可能会同时运行这段代码,如果每次运行的代码结果和单线程运行的结果是一样的,且其他变量的值和预期的也是一样的,那么就是线程安全的。 一个类或者程序…...

Golang | Leetcode Golang题解之第260题只出现一次的数字III
题目: 题解: func singleNumber(nums []int) []int {xorSum : 0for _, num : range nums {xorSum ^ num}lsb : xorSum & -xorSumtype1, type2 : 0, 0for _, num : range nums {if num&lsb > 0 {type1 ^ num} else {type2 ^ num}}return []in…...

IDEA自带的Maven 3.9.x无法刷新http nexus私服
问题: 自建的私服,配置了域名,使用http协议,在IDEA中或本地Maven 3.9.x会出现报错,提示http被blocked,原因是Maven 3.8.1开始,Maven默认禁止使用HTTP仓库地址,只允许使用HTTPS仓库地…...

56、本地数据库迁移到阿里云
现有需求,本地数据库迁移到阿里云上。 库名xy102表 test01test02test01 test023条数据。1、登录阿里云界面创建免费试用ECS实列。 阿里云登录页 (aliyun.com)](https://account.aliyun.com/login/login.htm?oauth_callbackhttps%3A%2F%2Fusercenter2.aliyun.com%…...

新时代多目标优化【数学建模】领域的极致探索——数学规划模型
目录 例1 1.问题重述 2.基本模型 变量定义: 目标函数: 约束条件: 3.模型分析与假设 4.模型求解 5.LINGO代码实现 6.结果解释 编辑 7.敏感性分析 8.结果解释 例2 奶制品的销售计划 1.问题重述 编辑 2.基本模型 3.模…...

单例模式详解
文章目录 一、概述1.单例模式2.单例模式的特点3.单例模式的实现方法 二、单例模式的实现1. 饿汉式2. 懒汉式3. 双重校验锁4. 静态内部类5. 枚举 三、总结 一、概述 1.单例模式 单例模式(Singleton Pattern)是一种创建型设计模式,确保一个类…...

WebGIS主流的客户端框架比较|OpenLayers|Leaflet|Cesium
实现 WebGIS 应用的主流前端框架主要包括 OpenLayers、Leaflet、Mapbox GL JS 和 Cesium 等。每个框架都有其独特的功能和优势,适合不同的应用场景。 WebGIS主流前端框架的优缺点 前 端 框架优点缺点OpenLayers较重量级的开源库,二维GIS功能最丰富全面…...

【LabVIEW作业篇 - 2】:分数判断、按钮控制while循环暂停、单击按钮获取book文本
文章目录 分数判断按钮控制while循环暂停按钮控制单个while循环暂停 按钮控制多个while循环暂停单击按钮获取book文本 分数判断 限定整型数值输入控件值得输入范围,范围在0-100之间,判断整型数值输入控件的输入值。 输入范围在0-59之间,显示…...
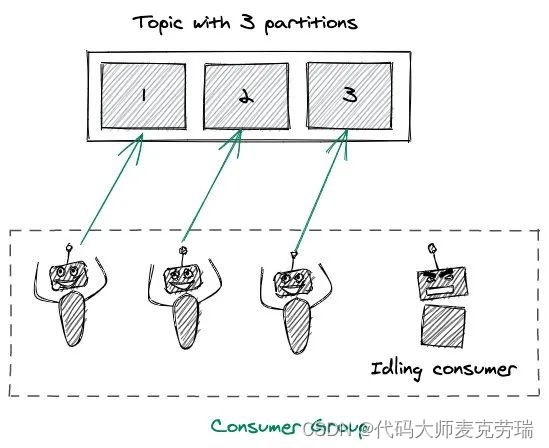
Kafka架构详解之分区Partition
目录 一、简介二、架构三、分区Partition1.分区概念2.Offsets(偏移量)和消息的顺序3.分区如何为Kafka提供扩展能力4.producer写入策略5.consumer消费机制 一、简介 Apache Kafka 是分布式发布 - 订阅消息系统,在 kafka 官网上对 kafka 的定义…...

SSM之Mybatis
SSM之Mybatis 一、MyBatis简介1、MyBatis特性2、MyBatis的下载3、MyBatis和其他持久化层技术对比 二、MyBatis框架搭建三、MyBatis基础功能1、MyBatis核心配置文件2、MyBatis映射文件3、MyBatis实现增删改查4、MyBatis获取参数值的两种方式5、MyBatis查询功能6、MyBatis自定义映…...

Python list comprehension (列表推导式 - 列表解析式 - 列表生成式)
Python list comprehension {列表推导式 - 列表解析式 - 列表生成式} 1. Python list comprehension (列表推导式 - 列表解析式 - 列表生成式)2. Example3. ExampleReferences Python 中的列表解析式并不是用来解决全新的问题,只是为解决已有问题提供新的语法。 列…...

2024年7月12日理发记录
上周五天气还算好,不太热,晚上下班打车回家后,将目的地设置成日常去的那个理发店。 下车走到门口,熟悉的托尼帅哥正在抽烟,他一眼看到了我,马上掐灭烟头,从怀里拿出口香糖,咀嚼起来&…...

几种常用排序算法
1 基本概念 排序是处理数据的一种最常见的操作,所谓排序就是将数据按某字段规律排列,所谓的字段就是数据节点的其中一个属性。比如一个班级的学生,其字段就有学号、姓名、班级、分数等等,我们既可以针对学号排序,也可…...

Spring3(代理模式 Spring1案例补充 Aop 面试题)
一、代理模式 在代理模式(Proxy Pattern)中,一个类代表另一个类的功能,这种类型的设计模式属于结构型模式。 代理模式通过引入一个代理对象来控制对原对象的访问。代理对象在客户端和目标对象之间充当中介,负责将客户端…...

Github报错:Kex_exchange_identification: Connection closed by remote host
文章目录 1. 背景介绍2. 排查和解决方案 1. 背景介绍 Github提交或者拉取代码时,报错如下: Kex_exchange_identification: Connection closed by remote host fatal: Could not read from remote repository.Please make sure you have the correct ac…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
