概率论原理精解【1】
文章目录
- 测度
- 概述
- 集类
- 笛卡尔积
- 定义
- 例子
- 多集合的笛卡尔积
- 定义
- 计算方法
- 注意事项
- 有限笛卡尔积的性质
- 1. 定义
- 2. 性质
- 2.1 基数性质
- 2.2 空集性质
- 2.3 不满足交换律
- 2.4 不满足结合律
- 2.5 对并和交运算满足分配律
- 3. 示例
- 4. 结论
- 参考链接
测度
概述
- 所谓测度,通俗的讲就是测量几何区域的尺度。 我们知道直线上的闭区间的测度就是通常的线段长度; 平面上一个闭圆盘的测度就是它的面积。
- 一般的集合,我们能不能定义测度呢? 比如直线上所有有理数构成的集合,它的测度怎么衡量呢?
一个简单的办法, 就是先在每个有理点上找一个开区间覆盖它,就好比给它带个“帽子”。因为有理数集是可列集(就是可以像排自然一样排好队,一个个数出来,也叫可数集,见集合论)
所以我们可以让第n个有理数上盖的开区间长度是第一个有理数(比方是1)上盖的开区间长度的 2 n 2^n 2n分之一。 这样所有那些开区间的长度之和是个有限值(就是1上的开区间长度的2倍)。
我们让1上的开区间逐渐缩小趋向于一个点,那么所有区间的总长度也相应缩小,趋向于长度0。 这样我们就说有理数集的测度是0。 用上面这种方法定义的测度也叫外测度。
集类
- 是一个集合,但集合的元素也是集合。
- 设有非空集合G,G的子集构成了集类的元素。
- 指标集是用来给集类中的元素标注。
比如 G i : I ∈ I {G_i:I \in I} Gi:I∈I
I I I为指标集
⋂ i ∈ I G i = { g : g ∈ G i , ∀ i ∈ I } ⋃ i ∈ I G i = { g : g ∈ G i , ∀ i ∈ I } \bigcap\limits_{i \in I} G_i=\{g:g \in G_i,\forall i \in I\} \\\bigcup\limits_{i \in I} G_i=\{g:g \in G_i,\forall i \in I\} i∈I⋂Gi={g:g∈Gi,∀i∈I}i∈I⋃Gi={g:g∈Gi,∀i∈I} - 极限
给定一个集合序列 A n {A_n} An,它的上极限可以定义为在无穷多个 A n A_n An中都存在的元素的集合,而下极限则是只有有限个 A n A_n An不包含它的元素的集合。
集合列 A K 上极限集: lim k → ∞ ‾ A k = ⋂ j = 1 ∞ ⋃ k = j ∞ A k 下极限集 : lim k → ∞ ‾ = ⋃ j = 1 ∞ ⋂ k = j ∞ A k 集合列{A_K} \\上极限集:\overline{\lim\limits_{k\rightarrow\infty}}A_k=\displaystyle\bigcap_{j=1}^{\infty}\displaystyle\bigcup_{k=j}^{\infty}A_k \\下极限集: \lim_{\overline{k\rightarrow\infty}}=\displaystyle\bigcup_{j=1}^{\infty}\displaystyle\bigcap_{k=j}^{\infty}A_k 集合列AK上极限集:k→∞limAk=j=1⋂∞k=j⋃∞Ak下极限集:k→∞lim=j=1⋃∞k=j⋂∞Ak
设 { A n , n ≥ 1 } 是单调集列,则 { A n , n ≥ 1 收敛 } A n ↑ = > lim n → ∞ A n = ∪ n = 1 ∞ A n A n ↓ = > lim n → ∞ A n = ∩ n = 1 ∞ A n 设\{A_n,n \ge 1\}是单调集列,则\{A_n,n \ge 1收敛\} \\A_n\uparrow=>\lim_{n \rightarrow \infty}A_n=\cup_{n=1}^{\infty}A_n \\A_n\downarrow=>\lim_{n \rightarrow \infty}A_n=\cap_{n=1}^{\infty}A_n 设{An,n≥1}是单调集列,则{An,n≥1收敛}An↑=>n→∞limAn=∪n=1∞AnAn↓=>n→∞limAn=∩n=1∞An - 值空间
A ⊂ X , A 在 f 下的像为 f ( A ) ,即: f ( A ) = { f ( x ) : x ∈ A } f ( A ) ⊂ Y Y 为值空间 A \subset X,A在f下的像为f(A),即: \\f(A)=\{f(x):x \in A\} \\f(A) \subset Y \\Y为值空间 A⊂X,A在f下的像为f(A),即:f(A)={f(x):x∈A}f(A)⊂YY为值空间
笛卡尔积
下面是文心一言的生成内容
笛卡尔积(Cartesian product)是数学中的一个概念,尤其在集合论、关系代数和计算机科学中非常重要。它指的是两个或多个集合中所有可能的有序元素对的集合。如果集合A有m个元素,集合B有n个元素,那么A和B的笛卡尔积将包含m * n个元素,即A中每一个元素都与B中每一个元素配对一次。
定义
设A和B是两个集合,A和B的笛卡尔积记作A × B,是一个集合,其元素是形如(a, b)的有序对,其中a属于A,b属于B。
例子
假设有两个集合:
- A = {1, 2}
- B = {x, y}
那么A和B的笛卡尔积A × B将是:
A × B = {(1, x), (1, y), (2, x), (2, y)}
这个集合包含了A中每个元素与B中每个元素的所有可能组合。
多集合的笛卡尔积
多集合的笛卡尔积(Cartesian product)是数学中的一个重要概念,它描述了多个集合之间所有可能的组合方式。笛卡尔积的结果是一个新的集合,其中的每个元素都是原集合中元素的组合。以下是关于多集合笛卡尔积的详细解释:
定义
对于给定的n个集合A1, A2, …, An,它们的笛卡尔积是一个新的集合,记作A1×A2×…×An,其中每个元素都是一个n元组(a1, a2, …, an),其中ai属于Ai(i=1, 2, …, n)。这个n元组表示从每个集合Ai中选取一个元素ai所形成的组合。
计算方法
-
两个集合的笛卡尔积:
- 假设有两个集合A和B,A有m个元素,B有n个元素。那么A和B的笛卡尔积A×B将有m×n个元素,每个元素都是一个有序对(a, b),其中a属于A,b属于B。
- 例如,A={1, 2},B={3, 4},则A×B={(1, 3), (1, 4), (2, 3), (2, 4)}。
-
多个集合的笛卡尔积:
- 可以通过迭代计算两个集合的笛卡尔积来得到多个集合的笛卡尔积。
- 首先计算前两个集合的笛卡尔积,然后将结果与下一个集合进行笛卡尔积计算,依此类推,直到与最后一个集合计算完成。
- 例如,对于集合A={a, b},B={0, 1},C={x, y},则首先计算A×B={(a, 0), (a, 1), (b, 0), (b, 1)},然后将结果与C进行笛卡尔积计算,得到A×B×C={(a, 0, x), (a, 0, y), (a, 1, x), (a, 1, y), (b, 0, x), (b, 0, y), (b, 1, x), (b, 1, y)}。
注意事项
- 笛卡尔积的大小随着集合数量的增加而呈指数级增长,因此在实际应用中需要注意性能和内存使用。
- 当处理大量数据时,可能需要考虑使用更高效的算法或优化策略来减少计算时间和内存消耗。
有限笛卡尔积的性质
有限笛卡尔积,即两个或多个有限集合之间的笛卡尔积,具有一系列重要的性质。以下是这些性质的详细归纳:
1. 定义
设A, B为集合,A和B的笛卡尔积是一个集合,其中每个元素都是一个有序对(x, y),其中x来自A,y来自B。记作A×B = {(x, y) | x∈A ∧ y∈B}。
2. 性质
2.1 基数性质
- 如果|A|=m(A的元素个数为m),|B|=n(B的元素个数为n),则|A×B|=mn。即笛卡尔积的元素个数是两个集合元素个数的乘积。
2.2 空集性质
- 当A或B为空集时,A×B也为空集,即A×B=∅。
2.3 不满足交换律
- 笛卡尔积运算不满足交换律,即当A≠B且A, B均非空时,A×B≠B×A。例如,设A={a,b},B={0,1},则A×B和B×A的元素顺序不同。
2.4 不满足结合律
- 笛卡尔积运算不满足结合律,即当A, B, C均非空时,(A×B)×C≠A×(B×C)。因为(A×B)×C的元素是形如((a,b),c)的有序对,而A×(B×C)的元素是形如(a,(b,c))的有序对,它们的结构不同。
2.5 对并和交运算满足分配律
- 笛卡尔积对并和交运算满足分配律,即:
- A×(B∪C)=(A×B)∪(A×C)
- (B∪C)×A=(B×A)∪(C×A)
- A×(B∩C)=(A×B)∩(A×C)
- (B∩C)×A=(B×A)∩(C×A)
这些性质表明,笛卡尔积在集合运算中具有很好的分配性。
3. 示例
设A={a,b},B={0,1},则:
- A×B={<a,0>,<a,1>,<b,0>,<b,1>}
- B×A={<0,a>,<0,b>,<1,a>,<1,b>}
这个示例直观地展示了笛卡尔积的构成以及不满足交换律的性质。
4. 结论
有限笛卡尔积是集合论中的一个重要概念,它具有独特的性质和广泛的应用。了解这些性质有助于更好地理解和运用笛卡尔积进行集合运算和逻辑推理。
以上信息基于多个权威来源的整合和分析,确保了信息的准确性和可靠性。
参考链接
1.测度论,百度百科
2.集合的极限
3. 《测度论与高等概率论》
相关文章:

概率论原理精解【1】
文章目录 测度概述集类笛卡尔积定义例子 多集合的笛卡尔积定义计算方法注意事项 有限笛卡尔积的性质1. 定义2. 性质2.1 基数性质2.2 空集性质2.3 不满足交换律2.4 不满足结合律2.5 对并和交运算满足分配律 3. 示例4. 结论 参考链接 测度 概述 所谓测度,通俗的讲就…...
数据结构(二叉树-1)
文章目录 一、树 1.1 树的概念与结构 1.2 树的相关术语 1.3 树的表示 二、二叉树 2.1 二叉树的概念与结构 2.2特殊的二叉树 满二叉树 完全二叉树 2.3 二叉树的存储结构 三、实现顺序结构二叉树 3.1 堆的概念与结构 3.2 堆的实现 Heap.h Heap.c 默认初始化堆 堆的销毁 堆的插入 …...

巴黎奥运会倒计时 一个非常不错的倒计时提醒
巴黎奥运会还有几天就要开幕了,大家应该到处都可以看到巴黎奥运会的倒计时,不管是电视上,还是网络里,一搜索奥运会,就会看到。倒计时其实是一个我们在生活中很常用的一个方法,用来做事情的提醒,…...

【Python】使用库 -- 详解
库就是别人已经写好了的代码,可以让我们直接拿来用。 一个编程语言能不能流行起来,一方面取决于语法是否简单方便容易学习,一方面取决于生态是否完备。所谓的 “生态” 指的就是语言是否有足够丰富的库,来应对各种各样的场景。在…...
Web3D:WebGL为什么在渲染性能上输给了WebGPU。
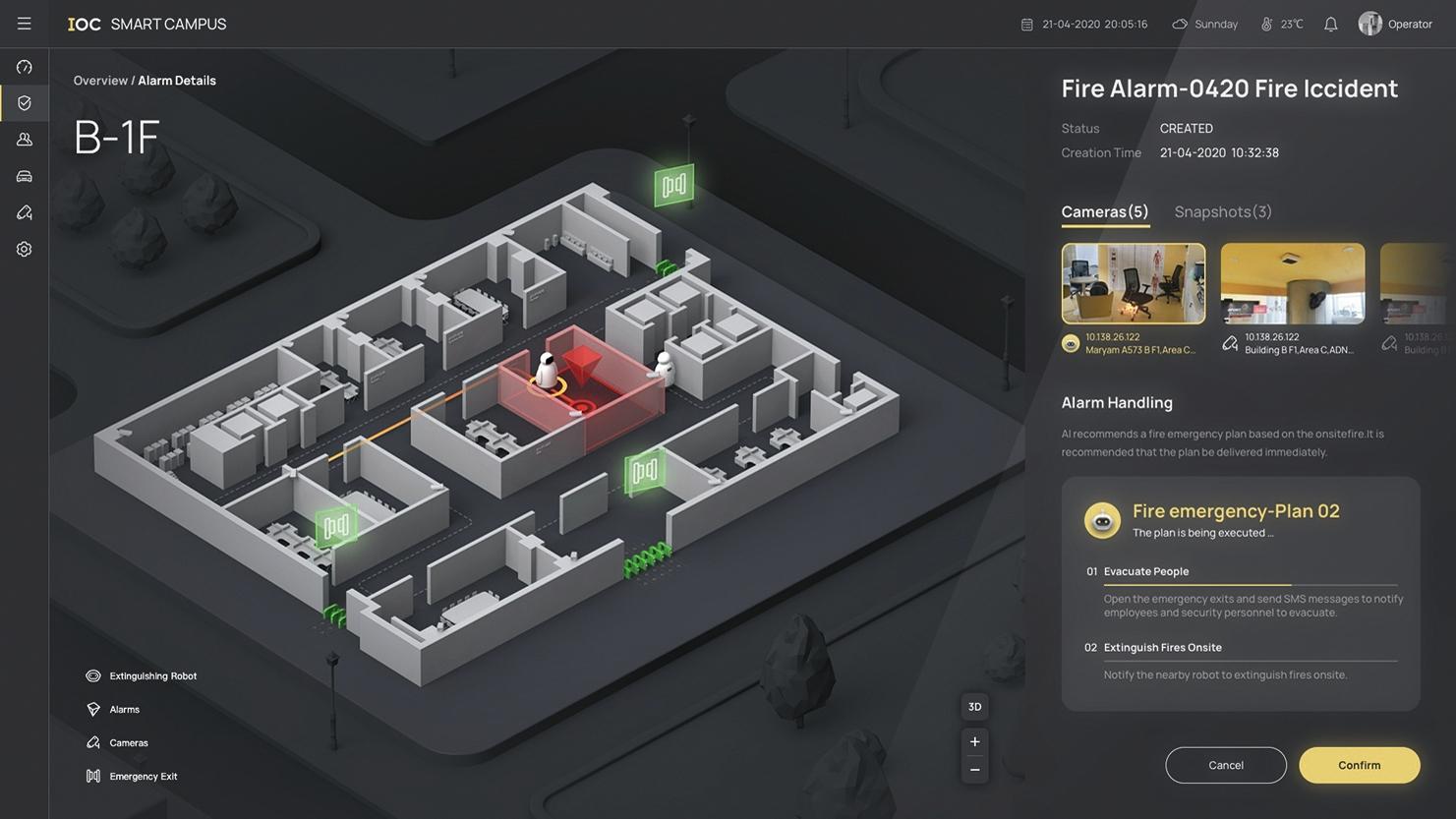
WebGL已经成为了web3D的标配,市面上有N多基于webGL的3D引擎,WebGPU作为挑战者,在渲染性能上确实改过webGL一头,由于起步较晚,想通过这个优势加持,赶上并超越webGL仍需时日。 贝格前端工场为大家分享一下这…...
SpringBoot面试高频总结01
1. 什么是SpringBoot? SpringBoot是一个基于Spring框架的快速开发框架,它采用约定大于配置,自动装配的方式,可以快速地创建独立的,生产级别的,基于Spring的应用程序。 相比于传统的Spring框架,S…...
:概念与实现)
Linux 工作队列(Workqueue):概念与实现
目录 一、工作队列的概念1.1 什么是工作队列1.2 为什么使用工作队列 二、工作队列的实现2.1 定义和初始化工作队列2.2 工作队列API 三、工作队列的应用3.1 延迟执行任务3.2 处理复杂的中断任务 四、工作队列的类型4.1 普通工作队列4.2 高优先级工作队列 五、总结 在Linux内核中…...

前端页面是如何禁止被查看源码、被下载,被爬取,以及破解方法
文章目录 1.了解禁止查看,爬取原理1.1.JS代码,屏蔽屏蔽键盘和鼠标右键1.2.查看源码时,通过JS控制浏览器窗口变化2.百度文库是如何防止抓包2.1.HTPPS2.2. 动态加载为什么看不到?如何查看动态加载的内容?3.禁止复制,如果解决3.1.禁止复制原理3.2.如何破解1.了解禁止查看,爬…...

51单片机嵌入式开发:14、STC89C52RC 之HX1838红外解码NEC+数码管+串口打印+LED显示
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 STC89C52RC 之HX1838红外解码NEC数码管串口打印LED显示 STC89C52RC 之HX1838红外解码NEC数码管串口打印LED显示1 概述2 硬件电路2.1 遥控器2.2 红外接收器电路2.3 STC89C52单…...

在不同环境中,Java应用程序和MySQL等是如何与Docker进行交互和操作的?
1. 本地开发环境 在本地开发环境中,可以使用Docker Compose来管理和运行Java应用程序容器和MySQL容器。通常,会创建一个docker-compose.yml文件,定义需要的服务及其配置。 以下是一个示例docker-compose.yml文件: version: 3 services:app…...
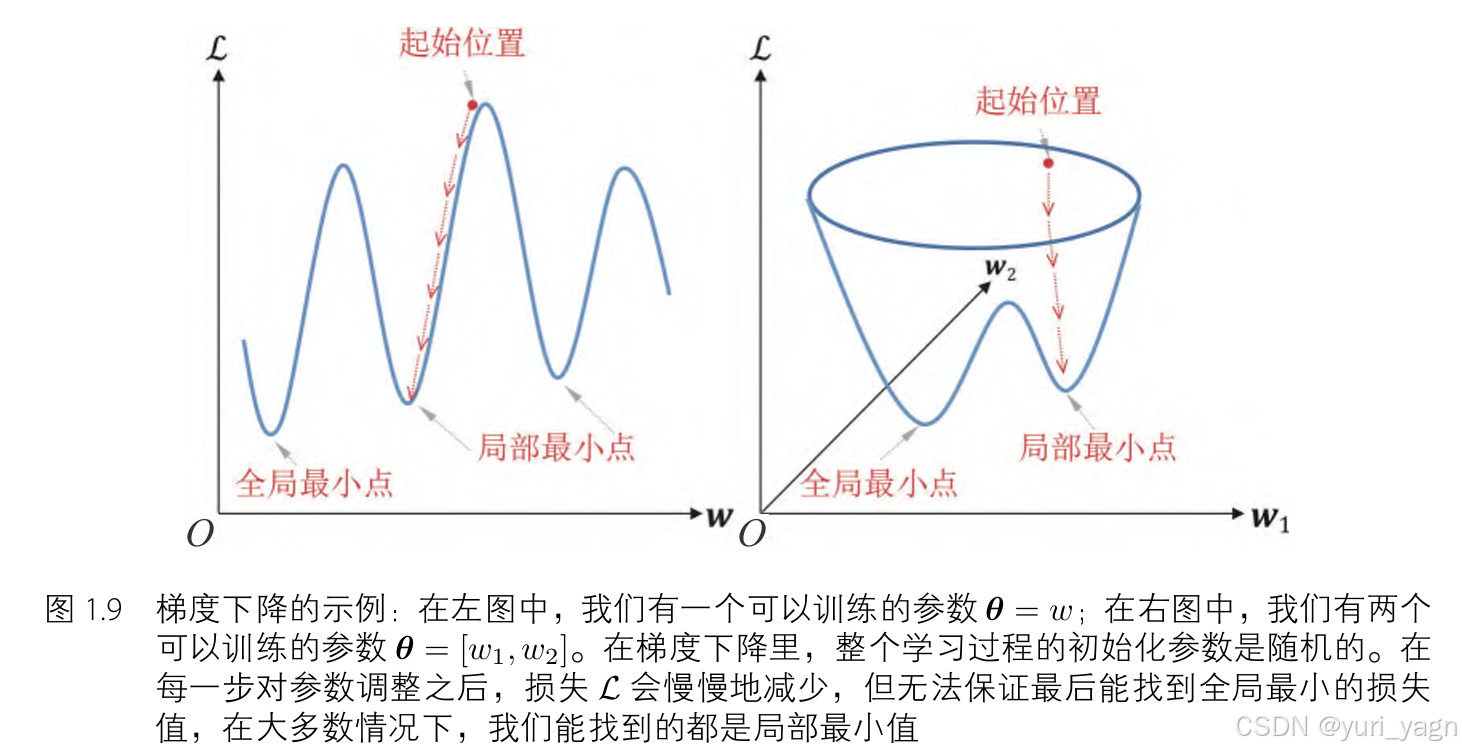
《DRL》P10-P15-损失函数-优化(梯度下降和误差的反向传播)
文章目录 损失函数交叉熵损失多类别分类任务概述真实标签的独热编码交叉熵损失函数 L p 范式 \mathcal{L}_{p}\text{ 范式} Lp 范式均方误差平均绝对误差 优化梯度下降和误差的反向传播 简介 本文介绍了神经网络中的损失函数及其优化方法。损失函数用于衡量模型预测值与真实值…...

Spring Boot项目的404是如何发生的
问题 在日常开发中,假如我们访问一个Sping容器中并不存在的路径,通常会返回404的报错,具体原因是什么呢? 结论 错误的访问会调用两次DispatcherServlet:第一次调用无法找到对应路径时,会给Response设置一个…...

<数据集>手势识别数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:2400张 标注数量(xml文件个数):2400 标注数量(txt文件个数):2400 标注类别数:5 标注类别名称:[fist, no_gesture, like, ok, palm] 序号类别名称图片数框数1fist597…...

【Vue3】选项式 API
【Vue3】选项式 API 背景简介开发环境开发步骤及源码总结 背景 随着年龄的增长,很多曾经烂熟于心的技术原理已被岁月摩擦得愈发模糊起来,技术出身的人总是很难放下一些执念,遂将这些知识整理成文,以纪念曾经努力学习奋斗的日子。…...

2、如何发行自己的数字代币(truffle智能合约项目实战)
2、如何发行自己的数字代币(truffle智能合约项目实战) 1-Atom IDE插件安装2-truffle tutorialtoken3-tutorialtoken源码框架分析4-安装openzeppelin代币框架(代币发布成功) 1-Atom IDE插件安装 正式介绍基于web的智能合约开发 推…...

百日筑基第二十三天-23种设计模式-创建型总汇
百日筑基第二十三天-23种设计模式-创建型总汇 前言 设计模式可以说是对于七大设计原则的实现。 总体来说设计模式分为三大类: 创建型模式,共五种:单例模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式。结构型模式,共…...

张量的基本使用
目录 1.张量的定义 2.张量的分类 3.张量的创建 3.1 根据已有数据创建张量 3.2 根据形状创建张量 3.3 创建指定类型的张量 1.张量的定义 张量(Tensor)是机器学习的基本构建模块,是以数字方式表示数据的形式。PyTorch就是将数据封装成张量…...
什么是唯一键(Unique Key)?)
Oracle(14)什么是唯一键(Unique Key)?
唯一键(Unique Key)是数据库表中的一个或多个列,它们的值必须在整个表中唯一,但允许包含NULL值。唯一键的主要目的是确保表中每一行的数据在指定的列(或列组合)中是唯一的,以防止重复数据的出现…...

PostgreSQL的引号、数据类型转换和数据类型
一、单引号和双引号(重要): 1、在mysql没啥区别 2、在pgsql中,实际字符串用单引号,双引号相当于mysql的,用来包含关键字; -- 单引号,表示user_name的字符串实际值 insert into t_user(user_nam…...
)
Mad MAD Sum-Codeforces Round 960 (Div. 2)
题目在这里 大意: MAD函数返回出现次数 ≥ 2 \geq2 ≥2的最大整数 b i b_i bi M A D ( a [ 1 , 2 , . . . i ] ) MAD(a[1,2,...i]) MAD(a[1,2,...i]) 每次操作把 a i a_i ai进行上述操作,直到全变为0为止,对每次操作的数组进行求和,记…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
