【信号频率估计】MVDR算法及MATLAB仿真
目录
- 一、MVDR算法
- 1.1 简介
- 1.2 原理
- 1.3 特点
- 1.3.1 优点
- 1.3.2 缺点
- 二、算法应用实例
- 2.1 信号的频率估计
- 2.2 MATLAB仿真代码
- 三、参考文献
一、MVDR算法
1.1 简介
最小方差无失真响应(Mininum Variance Distortionless Response,MVDR)算法最早是J. Capon于1969年提出,用于多维地震阵列传感器的频率-波数分析。随后,Lacoss在1971年将其引入到一维时间序列的分析中。
MVDR算法由于是Capon提出的,所以也将其称为Capon算法。
1.2 原理
根据数字波束形成的原理,得到输入信号 x ( n ) x(n) x(n) 经空域滤波后的输出为:
y ( n ) = w H x ( n ) = w H a ( θ ) s ( n ) ( 1 − 1 ) y(n)=w^{H}x(n)=w^{H}a(θ)s(n) (1-1) y(n)=wHx(n)=wHa(θ)s(n)(1−1)
其中,输入信号 x ( n ) x(n) x(n) 为期望、干扰、噪声三种信号的耦合; a ( θ ) a(θ) a(θ) 为导向矢量。
当一个远场窄带信号 s ( n ) s(n) s(n) 入射到 M 个阵元的均匀线阵时,阵列输出信号的平均功率为:
P ( θ ) = E [ ∣ y ( n ) ∣ 2 ] = E [ w H x ( n ) x H ( n ) w ] = w H R w ( 1 − 2 ) P(θ)=E[|y(n)|^2]=E[w^{H}x(n)x^{H}(n)w]=w^{H}Rw (1-2) P(θ)=E[∣y(n)∣2]=E[wHx(n)xH(n)w]=wHRw(1−2)
式(1-2)中 R = E [ x ( n ) x H ( n ) ] R=E[x(n)x^{H}(n)] R=E[x(n)xH(n)] 为接收信号 x ( n ) x(n) x(n) 的空间相关矩阵。
假设期望信号从 θ 0 θ_{0} θ0 方向入射,阵列接收信号为 x 0 ( n ) = a ( θ 0 ) s ( n ) x_{0}(n)=a(θ_{0})s(n) x0(n)=a(θ0)s(n) ,为了使 x 0 ( n ) x_{0}(n) x0(n) 通过空域滤波器后无失真,权矢量 w w w 需满足:
w H a ( θ 0 ) = 1 ( 1 − 3 ) w^{H}a(θ_{0})=1 (1-3) wHa(θ0)=1(1−3)
选择的加权矢量 w w w 满足式(1-3)就可以实现对干扰信号以及噪声的抑制,从而使输出信号的平均功率 P ( θ ) P(θ) P(θ) 最小。由此可以建立目标优化方程为:

采用拉格朗日乘数法对式(1-4)构造代价函数为:
J ( w ) = w H R w + λ ( w H a ( θ 0 ) − 1 ) ( 1 − 5 ) J(w)=w^{H}Rw+λ(w^{H}a(θ_{0})-1) (1-5) J(w)=wHRw+λ(wHa(θ0)−1)(1−5)
对式(1-5)关于 w w w 求梯度,并令其为零,得到:
▽ J ( w ) = 2 R w − 2 λ a ( θ 0 ) = 0 ( 1 − 6 ) ▽J(w)=2Rw-2λa(θ_{0})=0 (1-6) ▽J(w)=2Rw−2λa(θ0)=0(1−6)
解得: w = λ R − 1 a ( θ 0 ) w=λR^{-1}a(θ_{0}) w=λR−1a(θ0) ,将结果代入式(1-3)可得:
λ = 1 a H ( θ 0 ) R − 1 a ( θ 0 ) ( 1 − 7 ) λ=\frac{1}{a^{H}(θ_{0})R^{-1}a(θ_{0})} (1-7) λ=aH(θ0)R−1a(θ0)1(1−7)
将式(1-7)代入求得的权矢量结果中,可得到 MVDR 波束形成器的最优权向量为:
w o p t = R − 1 a ( θ 0 ) a H ( θ 0 ) R − 1 a ( θ 0 ) ( 1 − 8 ) w_{opt}=\frac{R^{-1}a(θ_{0})}{a^{H}(θ_{0})R^{-1}a(θ_{0})} (1-8) wopt=aH(θ0)R−1a(θ0)R−1a(θ0)(1−8)
以上就是 MVDR 波束形成求权值的完整过程。当阵列的阵元个数为 M M M 时,阵列的自由度为 M − 1 M-1 M−1,所以 MVDR 波束形成器要求干扰源个数必须小于或等于 M − 1 M-1 M−1。
在实际情况中,阵列的接收数据协方差矩阵只能在有限次快拍的情况下,用时间平均对采样数据进行估计得到,即:
R ˆ = 1 N ∑ n = 1 N x ( n ) x H ( n ) ( 1 − 9 ) R^{ˆ}=\frac{1}{N}\sum_{n=1}^{N}x(n)x^{H}(n) (1-9) Rˆ=N1n=1∑Nx(n)xH(n)(1−9)
其中, N N N 是采样快拍数, N N N 值越大,估计矩阵 R ˆ R^{ˆ} Rˆ 更接近理想的相关矩阵 R R R。
1.3 特点
1.3.1 优点
(1)高分辨率:MVDR算法能够有效地分辨出多个声源的方向,具有较高的分辨率。这使得它在处理复杂声学环境时能够提供更准确的声源定位信息。
(2)鲁棒性强:MVDR算法对噪声和混响信号具有较强的鲁棒性。在存在噪声和混响的环境中,该算法能够较好地保持对声源方向的估计能力,提高系统的稳定性和可靠性。
(3)计算量相对较小:相较于一些更复杂的算法,MVDR算法的计算量相对较小,这使得它在实时性要求较高的应用场景中具有一定的优势。
(4)干扰抑制能力强:MVDR算法通过最小化其他方向的信号功率,能够有效地抑制多径干扰和噪声,提高信号的质量。这在无线通信、声纳和雷达等领域尤为重要。
1.3.2 缺点
(1)远场假设限制:MVDR算法假设声源位于远场,即声源与麦克风阵列之间的距离远大于阵列的尺寸。这一假设限制了算法在近场声源定位中的应用,因为对于近场声源,算法的定位精度会显著下降。
(2)对导向矢量误差敏感:MVDR算法的性能在很大程度上依赖于导向矢量的准确性。如果导向矢量存在误差,将会对算法的估计结果产生较大影响,降低定位精度。
(3)阵列尺寸限制:MVDR算法的性能与阵列尺寸有关。一般来说,阵列尺寸越大,算法的性能越好。然而,在实际应用中,受到成本和空间等因素的限制,阵列尺寸往往无法做到足够大,这可能会限制算法的性能。
(4)计算复杂度较高:尽管相对于一些更复杂的算法而言,MVDR算法的计算量较小,但在实时性要求极高的应用场景中,其计算复杂度仍然可能成为一个挑战。此外,为了获得更好的性能,可能需要对算法进行进一步的优化和加速。
二、算法应用实例
2.1 信号的频率估计
仿真1:对目标信号的到达角进行估计
设一维均匀线阵的阵元数目为8,其间距为半波长,有3个目标信号的到达角分别为-30°,0°,20°,利用MVDR算法对该目标信号进行到达角估计,计算结果如下图所示。
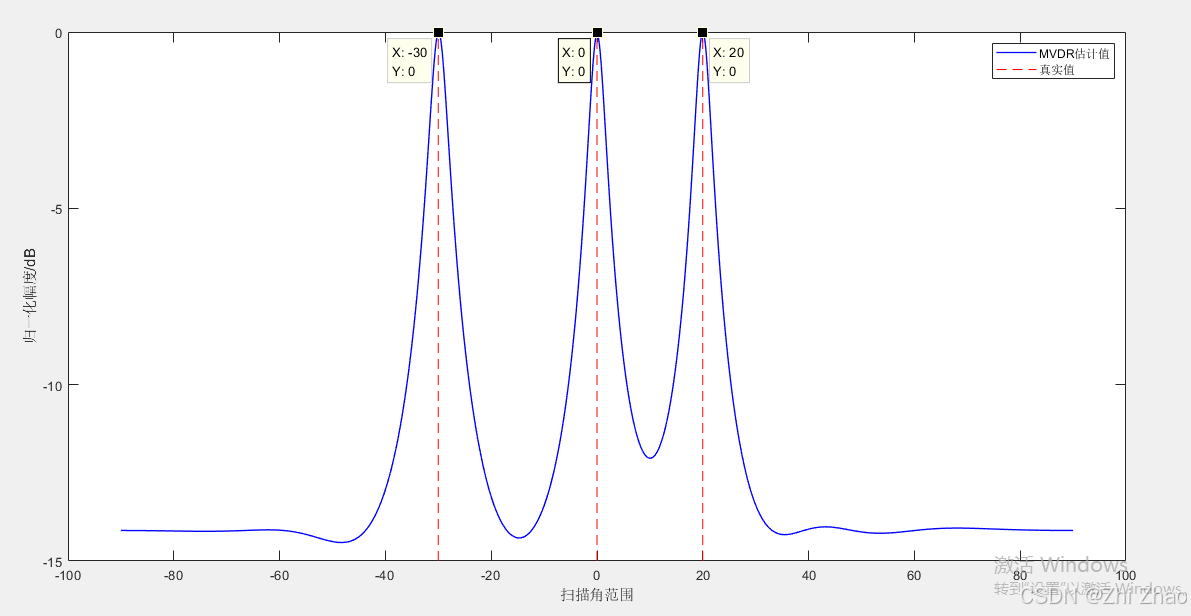
读者可根据自己的需求,设置阵元数、目标信号个数及目标真实角度、信号的信噪比等条件进行实验。
2.2 MATLAB仿真代码
clc;
clear;
close all;%% MVDR算法估计到达角
d_lambda = 0.5; % 阵元间距与波长比
Rx_Num = 8; % 接收天线阵元数N = 1000; % 采样快拍数
sigNum = 3; % 信源数目
theta0 = [-30,0,20]; % 真实来波角度
snr = 10; % 信噪比S = randn(sigNum,N)+1j*randn(sigNum,N); % 远场窄带信号
A = exp(1j*2*pi*d_lambda*sind(theta0).'*(0:Rx_Num-1)).'; % 导向矢量
X = A*S; % 接收信号
Y = awgn(X,snr,'measured'); % 添加噪声的接收信号R = Y*Y'/N; % 接收数据的协方差矩阵
R_ = inv(R); % 协方差矩阵的逆矩阵thetaScan = (-90:0.1:90); % 扫描角度范围
As = exp(1j*2*pi*d_lambda*sind(thetaScan).'*(0:Rx_Num-1)).';num = 0;
P = zeros(1,length(thetaScan)); % 谱峰函数初始化
for ii = thetaScannum = num+1;P(num) = 1/(As(:,num)'*R_*As(:,num));
end
P = 10*log10(abs(P)/max(abs(P))); % 对谱峰函数进行归一化并取对数
figure;
plot(thetaScan,P,'b','LineWidth',1);xlabel('扫描角范围');ylabel('归一化幅度/dB');hold on
ylim = get(gca,'Ylim');
for jj = 1:sigNum% 画出真实波达角的值进行对比line([theta0(jj) theta0(jj)],[ylim(1) ylim(2)],'Color','r','LineStyle','--');hold on;
end
legend('MVDR估计值','真实值');
三、参考文献
[1] Capon J. High-resolution frequency-wavenumber spectrum analysis[J]. Proc. IEEE, 1969, 57(8): 1408-1418.
[2] Lacoss R T. Data adaptive spectral analysis methods[J]. Geophysics, 1971, 36(8): 661-675.
[3] 胡君丽.数字阵列接收同时多波束技术研究[D].电子科技大学,2019.
相关文章:

【信号频率估计】MVDR算法及MATLAB仿真
目录 一、MVDR算法1.1 简介1.2 原理1.3 特点1.3.1 优点1.3.2 缺点 二、算法应用实例2.1 信号的频率估计2.2 MATLAB仿真代码 三、参考文献 一、MVDR算法 1.1 简介 最小方差无失真响应(Mininum Variance Distortionless Response,MVDR)算法最…...
HarmonyOS NEXT零基础入门到实战-第二部分
HarmonyOS NEXT零基础入门到实战-第二部分 Swiper 轮播组件 Swiper是一个 容器 组件,当设置了多个子组件后,可以对这些 子组件 进行轮播显示。(文字、图片...) 1、Swiper基本语法 2、Swiper常见属性 3、Swiper样式自定义 4、案例&…...
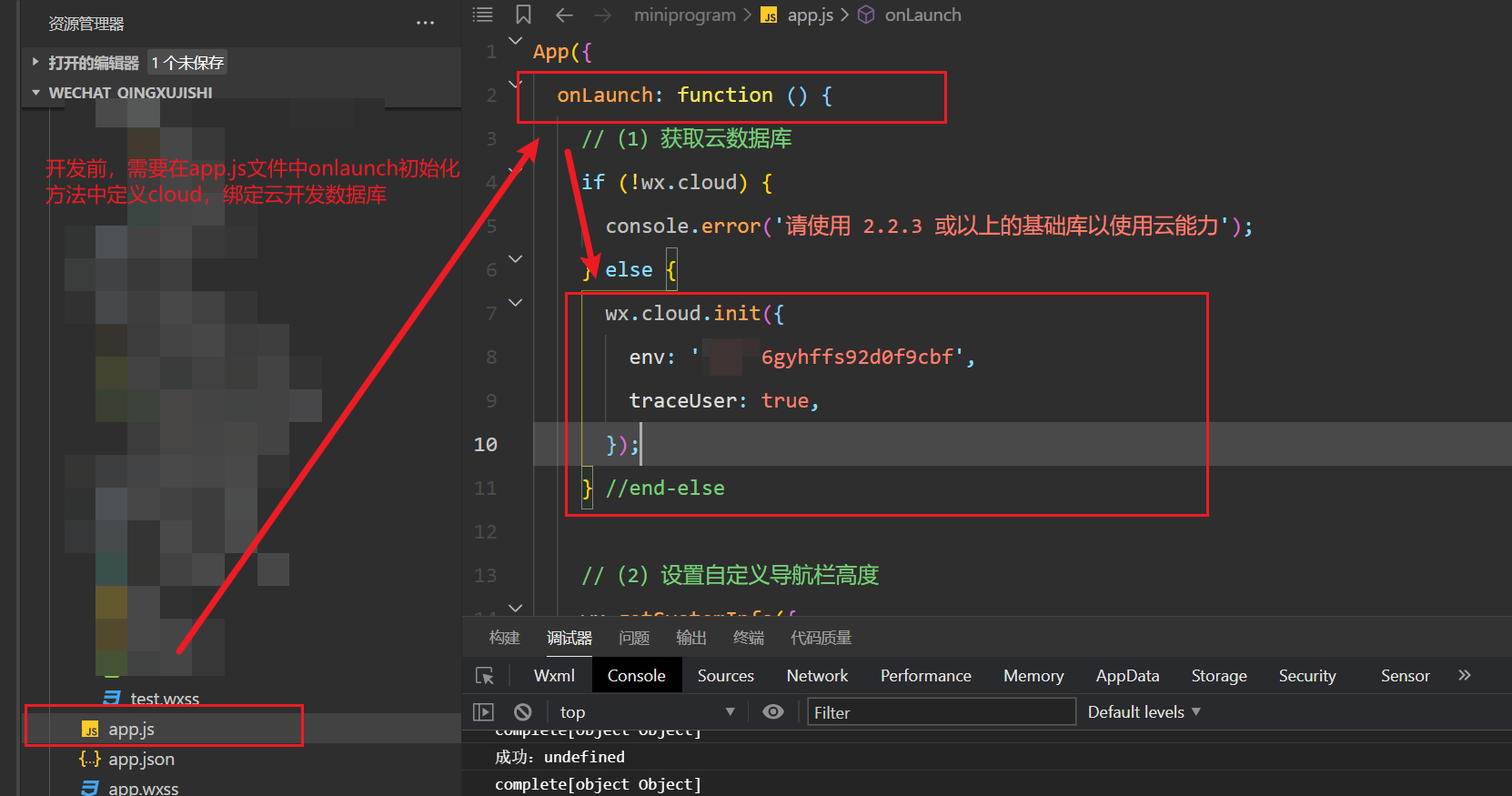
《小程序02:云开发之增删改查》
一、前置操作 // 一定要用这个符号包含里面的${}才会生效 wx.showToast({title: 获取数据成功:${colorLista}, })1.1:初始化介绍 **1、获取数据库引用:**在开始使用数据库 API 进行增删改查操作之前,需要先获取数据库的引用 cons…...
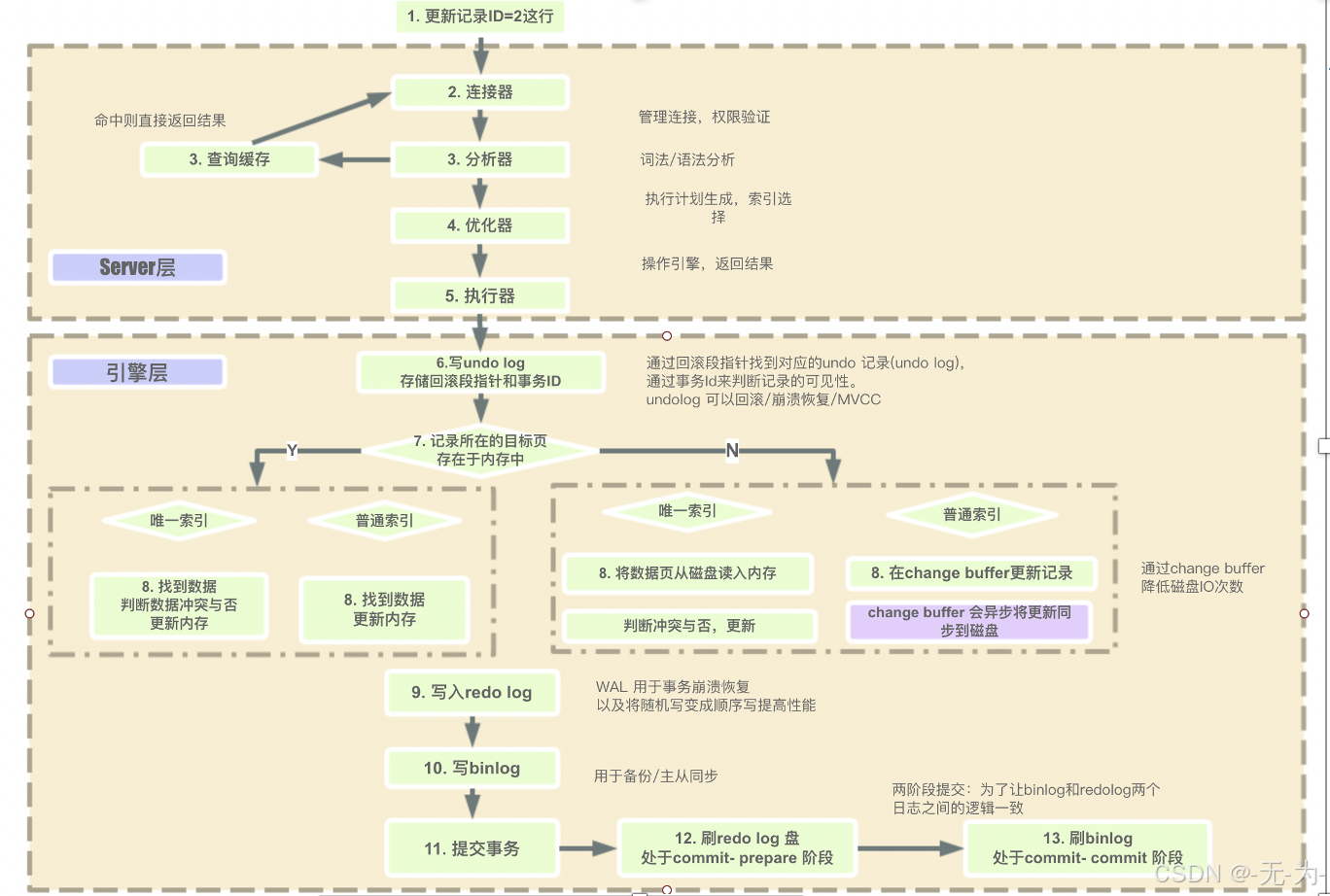
SQL执行流程、SQL执行计划、SQL优化
select查询语句 select查询语句中join连接是如何工作的? 1、INNER JOIN 返回两个表中的匹配行。 2、LEFT JOIN 返回左表中的所有记录以及右表中的匹配记录。 3、RIGHT JOIN 返回右表中的所有记录以及左表中的匹配记录。 4、FULL OUTER JOIN 返回左侧或右侧表中有匹…...

【前端】JavaScript入门及实战41-45
文章目录 41 嵌套的for循环42 for循环嵌套练习(1)43 for循环嵌套练习(2)44 break和continue45 质数练习补充 41 嵌套的for循环 <!DOCTYPE html> <html> <head> <title></title> <meta charset "utf-8"> <script type"…...
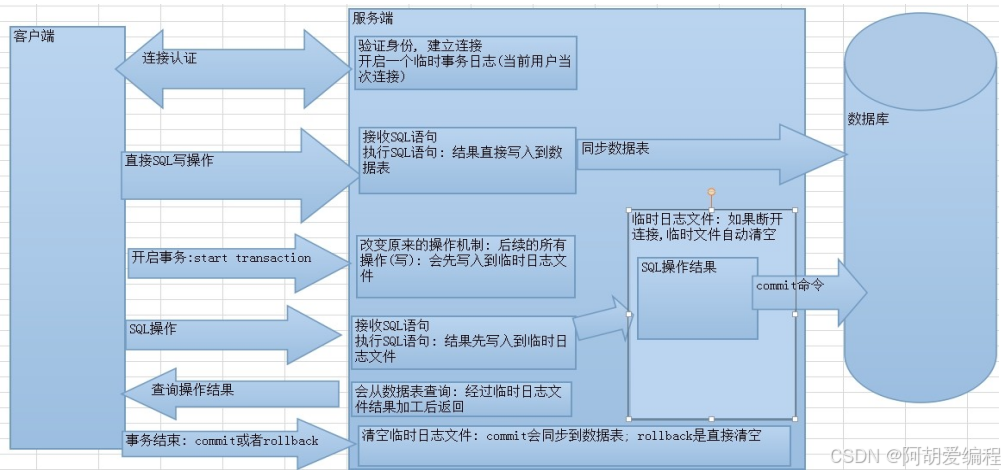
更加深入Mysql-04-MySQL 多表查询与事务的操作
文章目录 多表查询内连接隐式内连接显示内连接 外连接左外连接右外连接 子查询 事务事务隔离级别 多表查询 有时我们不仅需要一个表的数据,数据可能关联到俩个表或者三个表,这时我们就要进行夺标查询了。 数据准备: 创建一个部门表并且插入…...

基于最新版的flutter pointycastle: ^3.9.1的AES加密
基于最新版的flutter pointycastle: ^3.9.1的AES加密 自己添加pointycastle: ^3.9.1库config.dartaes_encrypt.dart 自己添加pointycastle: ^3.9.1库 config.dart import dart:convert; import dart:typed_data;class Config {static String password 成都推理计算科技; // …...

K8S内存资源配置
在 Kubernetes (k8s) 中,资源请求和限制用于管理容器的 CPU 和内存资源。配置 CPU 和内存资源时,使用特定的单位来表示资源的数量。 CPU 资源配置 CPU 单位:Kubernetes 中的 CPU 资源以 “核” (cores) 为单位。1 CPU 核心等于 1 vCPU/Core…...

【多任务YOLO】 A-YOLOM: You Only Look at Once for Real-Time and Generic Multi-Task
You Only Look at Once for Real-Time and Generic Multi-Task 论文链接:http://arxiv.org/abs/2310.01641 代码链接:https://github.com/JiayuanWang-JW/YOLOv8-multi-task 一、摘要 高精度、轻量级和实时响应性是实现自动驾驶的三个基本要求。本研究…...

数学建模--灰色关联分析法
目录 简介 基本原理 应用场景 优缺点 优点: 缺点: 延伸 灰色关联分析法在水质评价中的具体应用案例是什么? 如何克服灰色关联分析法在主观性强时的数据处理和改进方法? 灰色关联分析法与其他系统分析方法(如A…...
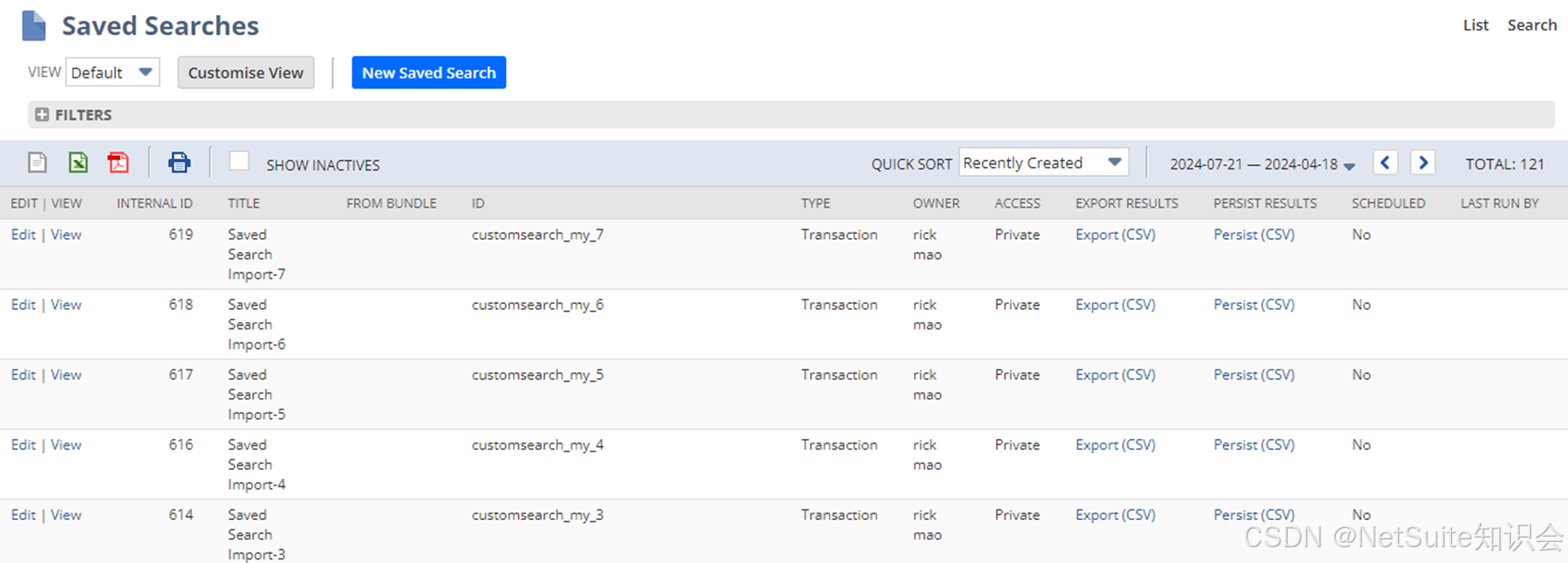
NetSuite Saved Search迁移工具
我们需要在系统间迁移Saved Search,但是采用Copy To Account或者Bundle时,会有一些Translation不能迁移,或者很多莫名其妙的Dependency,导致迁移失败。因此,我们想另辟蹊径,借助代码完成Saved Search的迁移…...
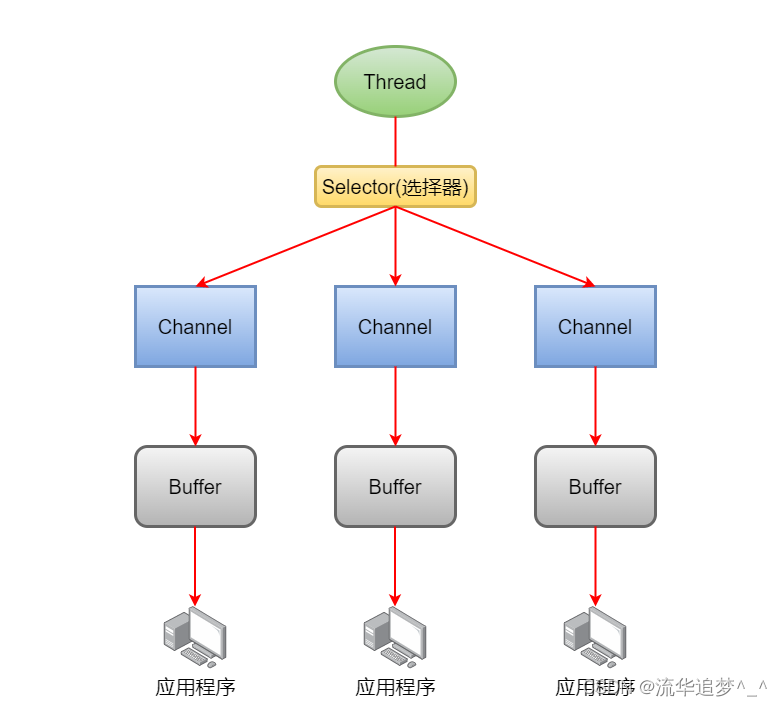
Java IO模型深入解析:BIO、NIO与AIO
Java IO模型深入解析:BIO、NIO与AIO 一. 前言 在Java编程中,IO(Input/Output)操作是不可或缺的一部分,它涉及到文件读写、网络通信等方面。Java提供了多种类和API来支持这些操作。本文将从IO的基础知识讲起ÿ…...
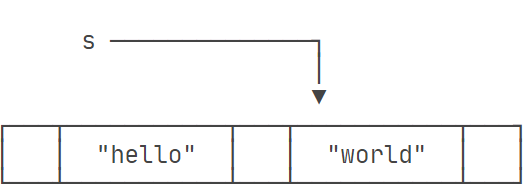
《从C/C++到Java入门指南》- 9.字符和字符串
字符和字符串 字符类型 Java 中一个字符保存一个Unicode字符,所以一个中文和一个英文字母都占用两个字节。 // 计算1 .. 100 public class Hello {public static void main(String[] args) {char a A;char b 中;System.out.println(a);System.out.println(b)…...
Adobe国际认证详解-视频剪辑
在数字化时代,视频剪辑已成为创意表达和视觉传播的重要手段。随着技术的不断进步,熟练掌握视频剪辑技能的专业人才需求日益增长。在这个背景下,Adobe国际认证应运而生,成为全球创意设计领域的重要标杆。 Adobe国际认证是由Adobe公…...

昇思25天学习打卡营第19天|MindNLP ChatGLM-6B StreamChat
文章目录 昇思MindSpore应用实践ChatGML-6B简介基于MindNLP的ChatGLM-6B StreamChat Reference 昇思MindSpore应用实践 本系列文章主要用于记录昇思25天学习打卡营的学习心得。 ChatGML-6B简介 ChatGLM-6B 是由清华大学和智谱AI联合研发的产品,是一个开源的、支持…...

.NET在游戏开发中有哪些成功的案例?
简述 在游戏开发的多彩世界中,技术的选择往往决定了作品的成败。.NET技术,以其跨平台的性能和强大的开发生态,逐渐成为游戏开发者的新宠。本文将带您探索那些利用.NET技术打造出的著名游戏案例,领略.NET在游戏开发中的卓越表现。 …...

搜维尔科技:我们用xsens完成了一系列高难度的运动项目并且捕获动作
我们用xsens完成了一系列高难度的运动项目并且捕获动作 搜维尔科技:我们用xsens完成了一系列高难度的运动项目并且捕获动作...

深入探讨:Node.js、Vue、SSH服务与SSH免密登录
在这篇博客中,我们将深入探讨如何在项目中使用Node.js和Vue,并配置SSH服务以及实现SSH免密登录。我们会一步步地进行讲解,并提供代码示例,确保你能轻松上手。 一、Node.js 与 Vue 的结合 1.1 Node.js 简介 Node.js 是一个基于 …...
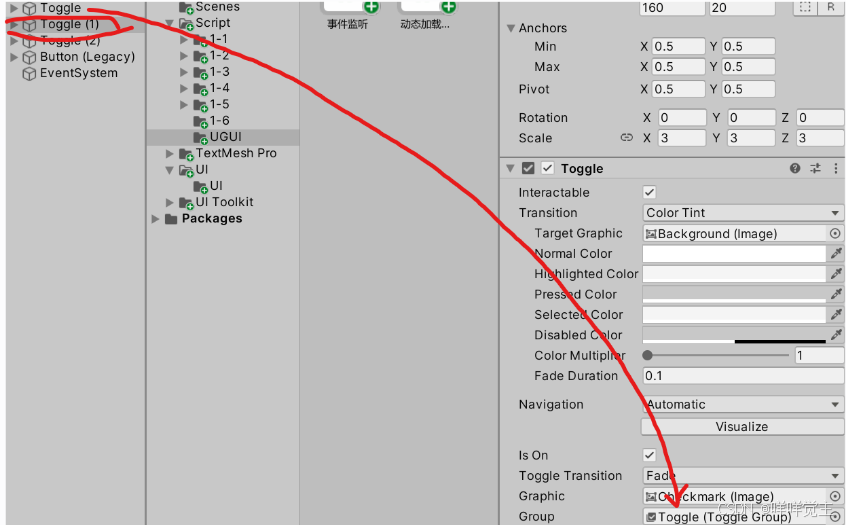
Unity UGUI 之 Toggle
本文仅作学习笔记与交流,不作任何商业用途本文包括但不限于unity官方手册,唐老狮,麦扣教程知识,引用会标记,如有不足还请斧正 1.什么是Toggle? Unity - Manual: Toggle 带复选框的开关,可…...

Git报错:error: fsmonitor--daemon failed to start处理方法
问题描述 git用了很久了,但是后面突然发现执行命令时,后面都会出现这个报错,虽然该报错好像不会影响正常的命令逻辑,但是还是感觉有天烦人,就去找了找资料。 $ git status error: fsmonitor--daemon failed to start…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
