关于利用FFT分析时域信号幅相的思考与验证

引言
利用FFT分析/估计时域信号的幅度和相位,属于传统估计的范畴。估计的准确程度受频率分辨率的影响较大。如果被估计的目标频率等于频率分辨率的整数倍,信号的幅相估计都是最准确的。一旦目标频率不等于频率分辨率的整数倍,幅度估计值将会降低,相位估计值会偏差很大。
下面会通过一些仿真来验证。
单点频实信号估计
信号幅值:10
信号相位:45°
信号频率:100Hz
信号类型:实信号
采样率:1000Hz
采样点数:100
频率分辨率:10Hz
信号频率等于分辨率整数倍
MATLAB代码:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=-pi/8;
N=100;
t=(0:N-1)/fs;
s=10*cos(2*pi*f0*t+p0);
figure;
subplot(311)
plot(s)
title('时域波形');xlabel('采样点数');ylabel('采样幅度')subplot(312)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(313)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')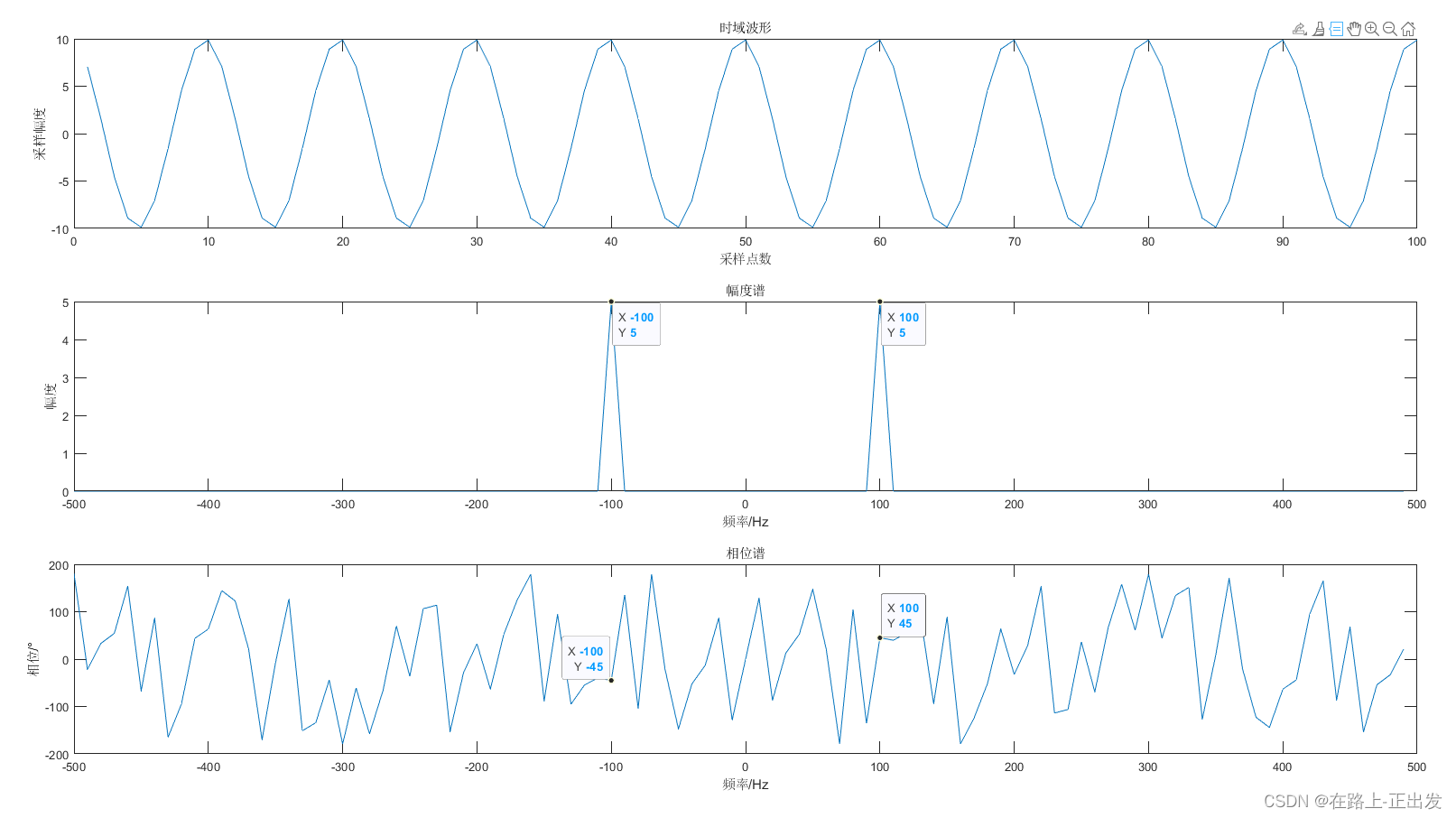
注意,此处分析的双边谱,所以每边高度为 10/2 = 5;
相位估计很准确,是45°相位。
信号频率不等于分辨率整数倍
如果改变采样点数(改为128),使得频率分辨率变化,不等于分辨率的整数倍,则:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=pi/4;
N=128;
t=(0:N-1)/fs;
s=10*cos(2*pi*f0*t+p0);
figure;
subplot(311)
plot(s)
title('时域波形');xlabel('采样点数');ylabel('采样幅度')subplot(312)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(313)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')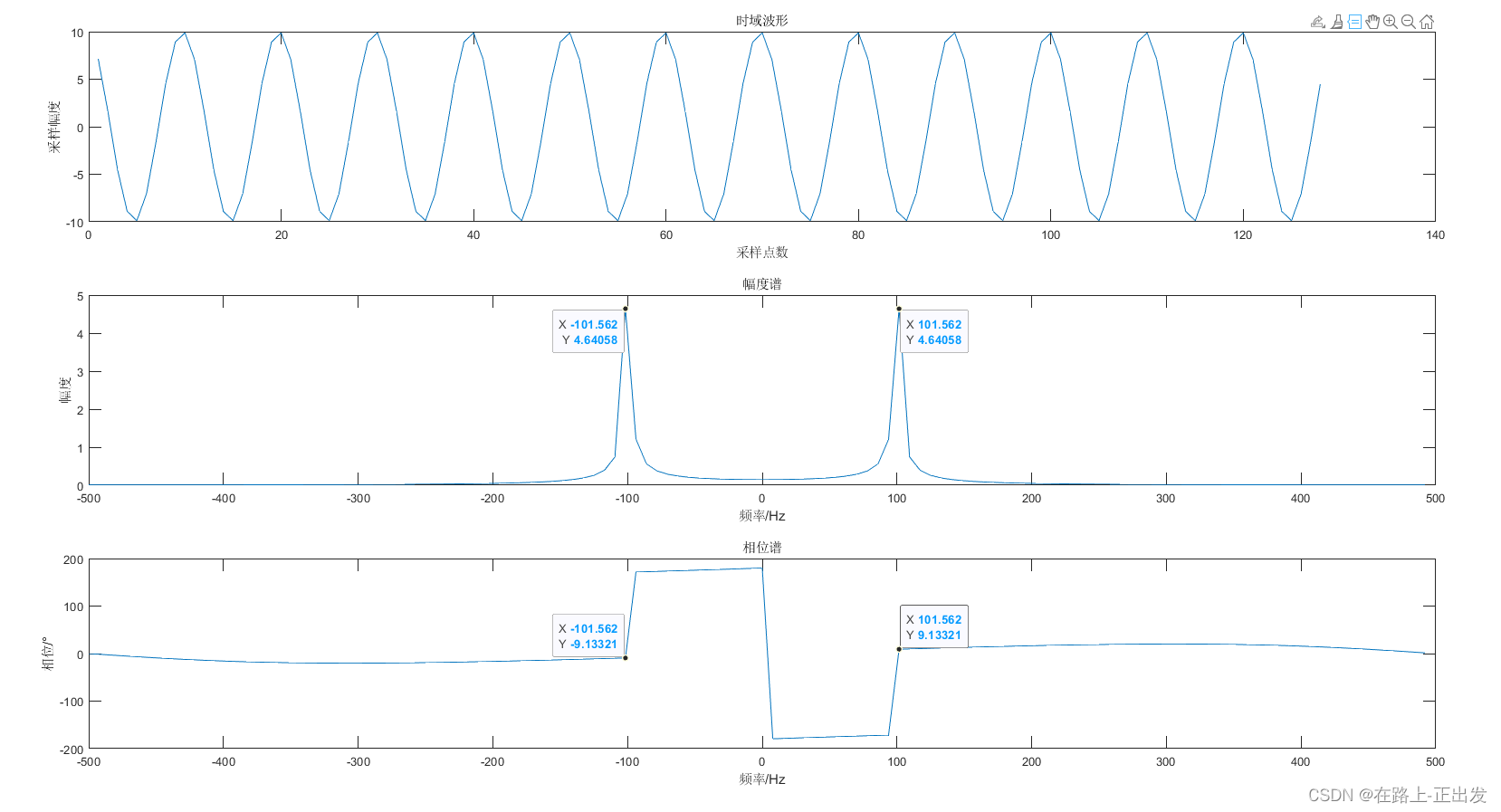
根据仿真结果,发现频率、幅度估值有微小偏差,相位的估计值几乎不可信。
信号频率等于分辨率整数倍,加噪声
考虑噪声影响:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=pi/4;
N=100;
t=(0:N-1)/fs;
s=10*cos(2*pi*f0*t+p0) + 2*randn(1,N);
figure;
subplot(311)
plot(s)
title('时域波形');xlabel('采样点数');ylabel('采样幅度')subplot(312)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(313)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')
根据仿真结果,信号的频率估计准确,但是幅度和相位的估计存在微小误差。
多点频实信号估计
信号的频点均位于频率分辨率整数倍的位置:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=pi/4;
f1=2e2;
p1=pi/2;
N=100;
t=(0:N-1)/fs;
s=10*cos(2*pi*f0*t+p0) + 4*cos(2*pi*f1*t+p1);
figure;
subplot(311)
plot(s)
title('时域波形');xlabel('采样点数');ylabel('采样幅度')subplot(312)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(313)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')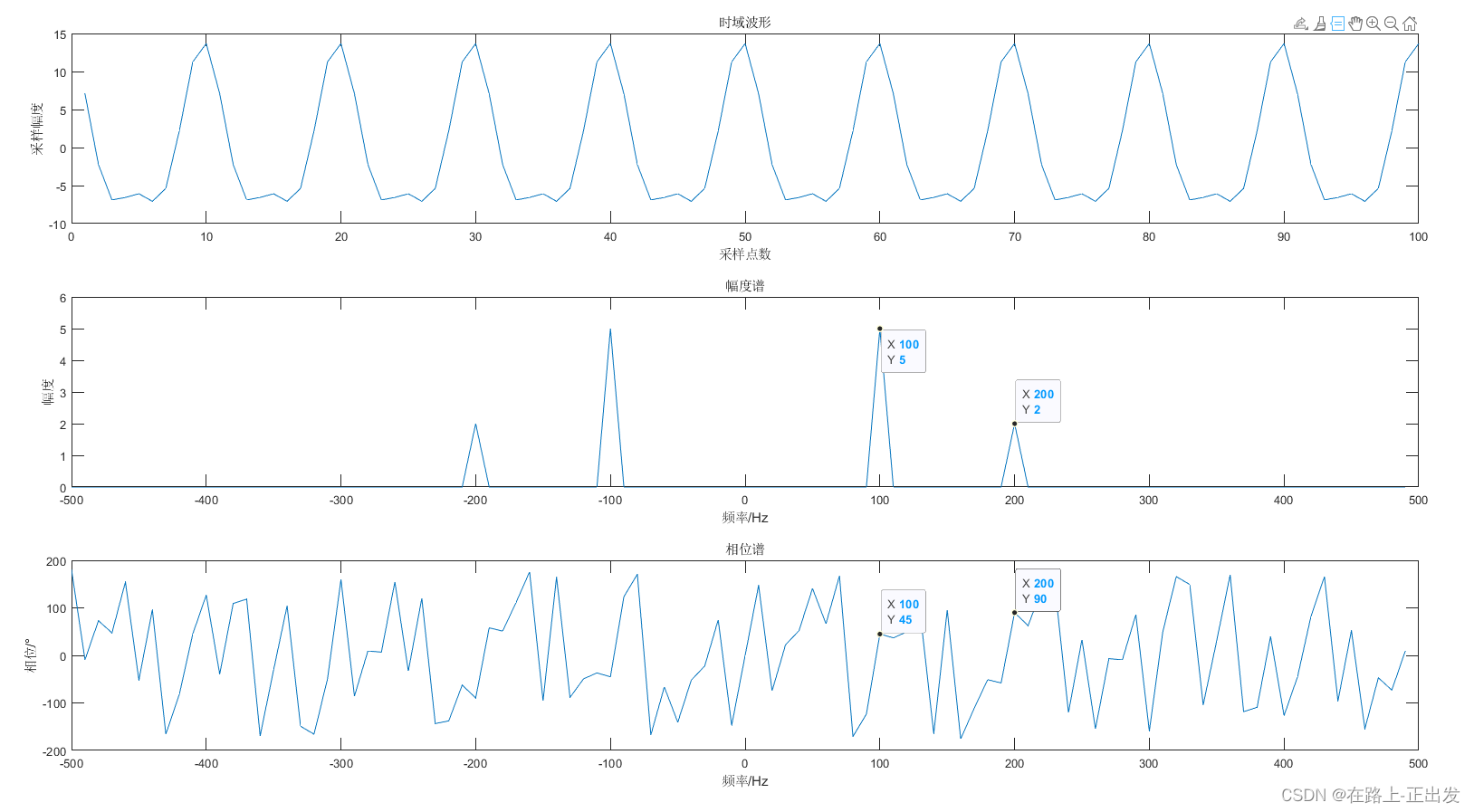
对于多点频信号,只要信号频点均位于分辨率整数倍的位置,其估值都十分准确。
多点频复信号估计
下面再试验一下复信号:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=pi/4;
f1=2e2;
p1=pi/2;
N=100;
t=(0:N-1)/fs;
s=10*exp(1j*(2*pi*f0*t+p0)) + 4*exp(1j*(2*pi*f1*t+p1));
figure;
subplot(411)
plot(real(s))
title('时域波形(实部)');xlabel('采样点数');ylabel('采样幅度')subplot(412)
plot(imag(s))
title('时域波形(虚部)');xlabel('采样点数');ylabel('采样幅度')subplot(413)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(414)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')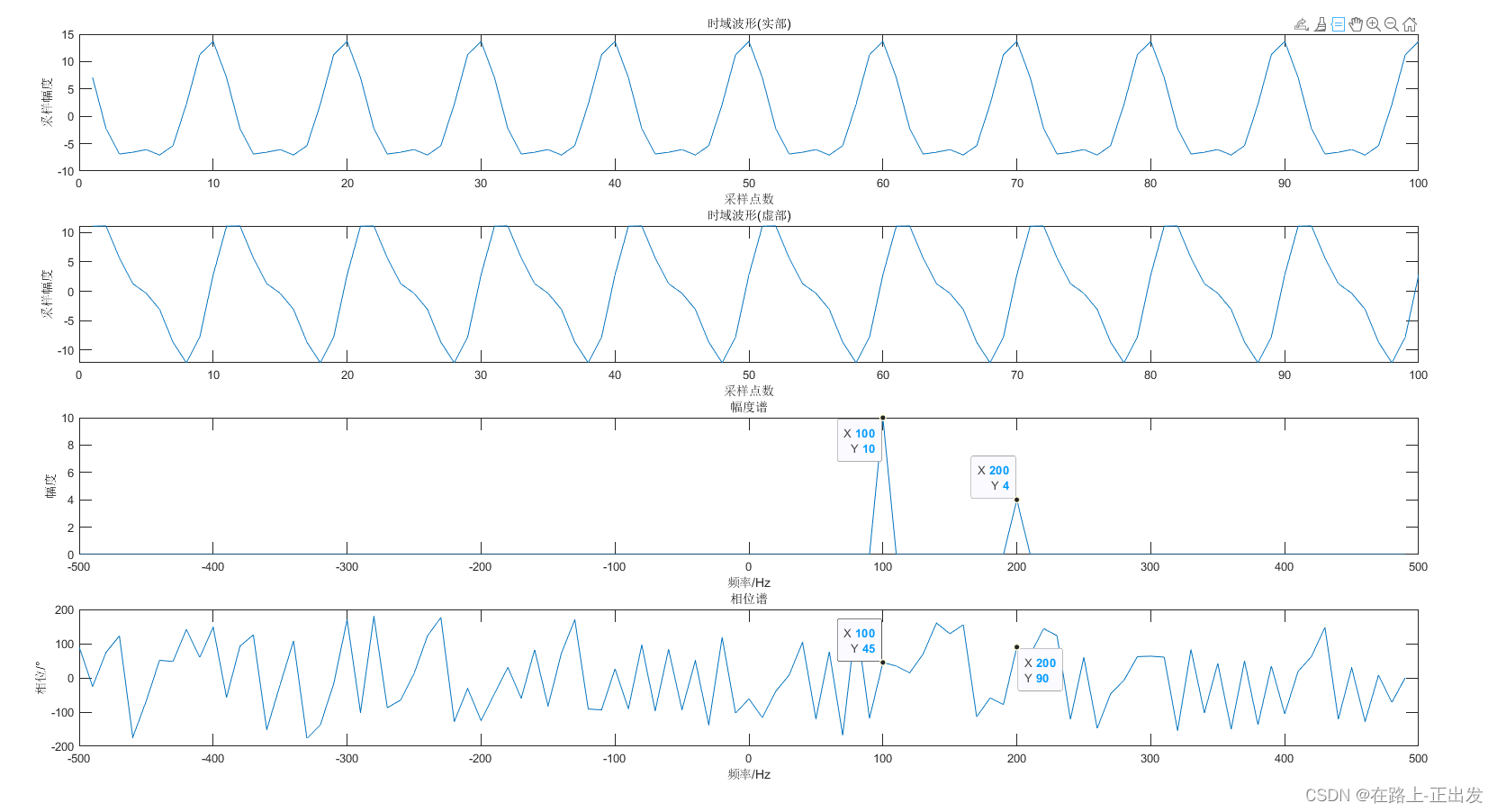
根据仿真结果,可以看出,复信号同样满足上述结论,即信号频率位于分辨率整数倍位置时,用FFT可以精确估计其频率和相位。
结论
结尾处再次说明一下:
不论是是信号还是复信号:
- 不加噪声时,位于分辨率整数倍处的信号频率、相位均可以被精确估算;
- 不加噪声时,不位于分辨率整数倍处的信号频率的估计存在微小误差、相位估计值基本不可信;
- 加噪声时,位于分辨率整数倍处的信号频率可以被精确估算,相位估算存在微小偏差;
可以结合代码和仿真进行理解,如有疑问,评论区留言吧~~
相关文章:

关于利用FFT分析时域信号幅相的思考与验证
引言 利用FFT分析/估计时域信号的幅度和相位,属于传统估计的范畴。估计的准确程度受频率分辨率的影响较大。如果被估计的目标频率等于频率分辨率的整数倍,信号的幅相估计都是最准确的。一旦目标频率不等于频率分辨率的整数倍,幅度估计值将会…...
基于java中的Springboot框架实现餐厅点餐系统展示
基于java中的Springboot框架实现餐厅点餐系统开发语言和工具 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 21世纪的今天,随着社会的不断发展与进步,人们对…...
案例07-在线人员列表逻辑混乱
一、背景介绍 在线人员列表涉及到的问题: 类中写了公共变量最后导致数据混乱现象 保存数据没有考虑业务的隔夜覆盖导致的逻辑漏洞 涉及到继承,对于this,如果父类有同样的成员最终使用哪一个? 参数不一致导致后续维护混乱 mysql由…...

Java集合框架
Java集合框架是Java编程语言所提供的一种便捷的数据结构的实现。Java集合框架提供了一种统一的接口和机制来访问和操作集合中的元素,这些元素可以是对象、基本数据类型或其他集合。Java集合框架是Java应用程序中最常用的特性之一,它为开发人员提供了许多…...
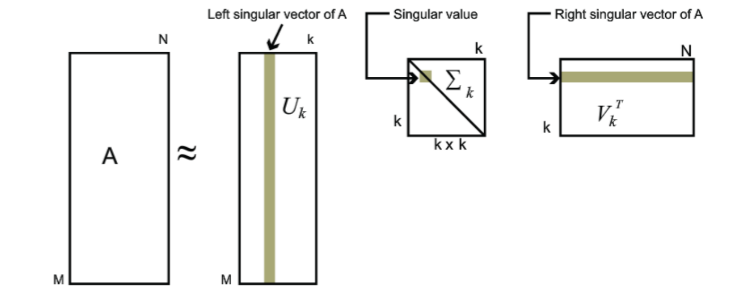
奇异值分解(SVD)原理与在降维中的应用
奇异值分解(SVD)原理与在降维中的应用 奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算…...

GDB调试程序
1.GDB 调试程序 GDB是GNU开源组织发布的一个强大的UNIX下的程序调试工具。在UNIX平台下做软件,GDB这个调试工具有比VC的图形化调试器更强大的功能。所谓“寸有所长,尺有所短”就是这个道理。 一般来说,GDB主要帮忙你完成下面四个方面的功能…...

五种IO模型
用户空间与内核空间 操作系统把内存空间划分成了两个部分:内核空间和用户空间。 为了保护内核空间的安全,操作系统一般都限制用户进程直接操作内核。 所以,当我们使用TCP发送数据的时候,需要先将数据从用户空间拷贝到内核空间&a…...

5 全面认识java的控制流程
全面认识java控制流程1.块作用域2.条件语句3.迭代语句3.1while语句3.2do-while语句3.3for语句3.4 for-in语法4.中断控制流程的语句4.1 return4.2 break和continue4.2.1 不带标签的break语句4.2.2 带标签的break语句4.2.3 continue语句4.3 goto()5.多重选择:switch语句1.块作用域…...

第二章 测验【嵌入式系统】
第二章 测验【嵌入式系统】前言推荐第二章 测验【嵌入式系统】最后前言 以下内容源自《嵌入式系统》 仅供学习交流使用 推荐 第一章 测验【嵌入式系统】 第二章 测验【嵌入式系统】 1单选题 32bit宽的数据0x12345678 在小端模式(Little-endian)模式…...

排序算法之插入排序
要考数据结构了,赶紧来复习一波排序算法 文章目录一、直接插入排序二、希尔排序一、直接插入排序 直接上主题 插排,揪出一个数,插入到原本已经有序的数组里面,如数组有n个数据,从0~n下标依次排列,先从左往…...
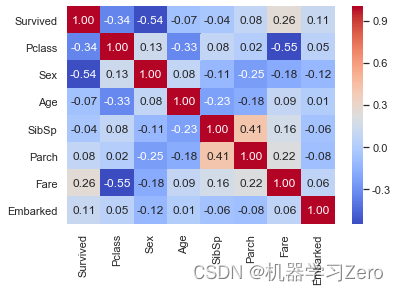
Kaggle实战入门:泰坦尼克号生生还预测
Kaggle实战入门:泰坦尼克号生生还预测1. 加载数据2. 特征工程3. 模型训练4. 模型部署泰坦尼克号(Titanic),又称铁达尼号,是当时世界上体积最庞大、内部设施最豪华的客运轮船,有“永不沉没”的美誉ÿ…...
)
【大汇总】11个Python开发经典错误(1)
“但是太阳,他每时每刻都是夕阳也都是旭日。当他熄灭着走下山去收尽苍凉残照之际,正是他在另一面燃烧着爬上山巅散烈烈朝晖之时。” --------史铁生《我与地坛》 🎯作者主页:追光者♂🔥 🌸个人简介:计算机专业硕士研究生💖、2022年CSDN博客之星人工智能领…...
Java中的异常
程序错误一般分为三种:编译错误: 编写程序时没有遵循语法规则,编译程序能够自己发现错误并提示位置和原因。运行错误:程序在执行的时候运行环境发现了不能执行的操作。比如,JVM出错了,内存溢出等。逻辑错误…...

L2-022 重排链表 L2-002 链表去重
给定一个单链表 L1 →L2→⋯→L n−1 →L n ,请编写程序将链表重新排列为 L n →L 1 →L n−1 →L 2 →⋯。例如:给定L为1→2→3→4→5→6,则输出应该为6→1→5→2→4→3。 输入格式: 每个输入包含1个测试用例。每个测试用例第1行…...
【手撕八大排序】——插入排序
文章目录插入排序概念插入排序分为2种一 .直接插入排序直接插入排序时间复杂度二.希尔排序希尔排序时间复杂度效率比较插入排序概念 直接插入排序是从一个有序的序列中选择一个合适的位置进行插入,这个合适的位置取决于是要升序排序还是降序排序。 每一次进行排序…...
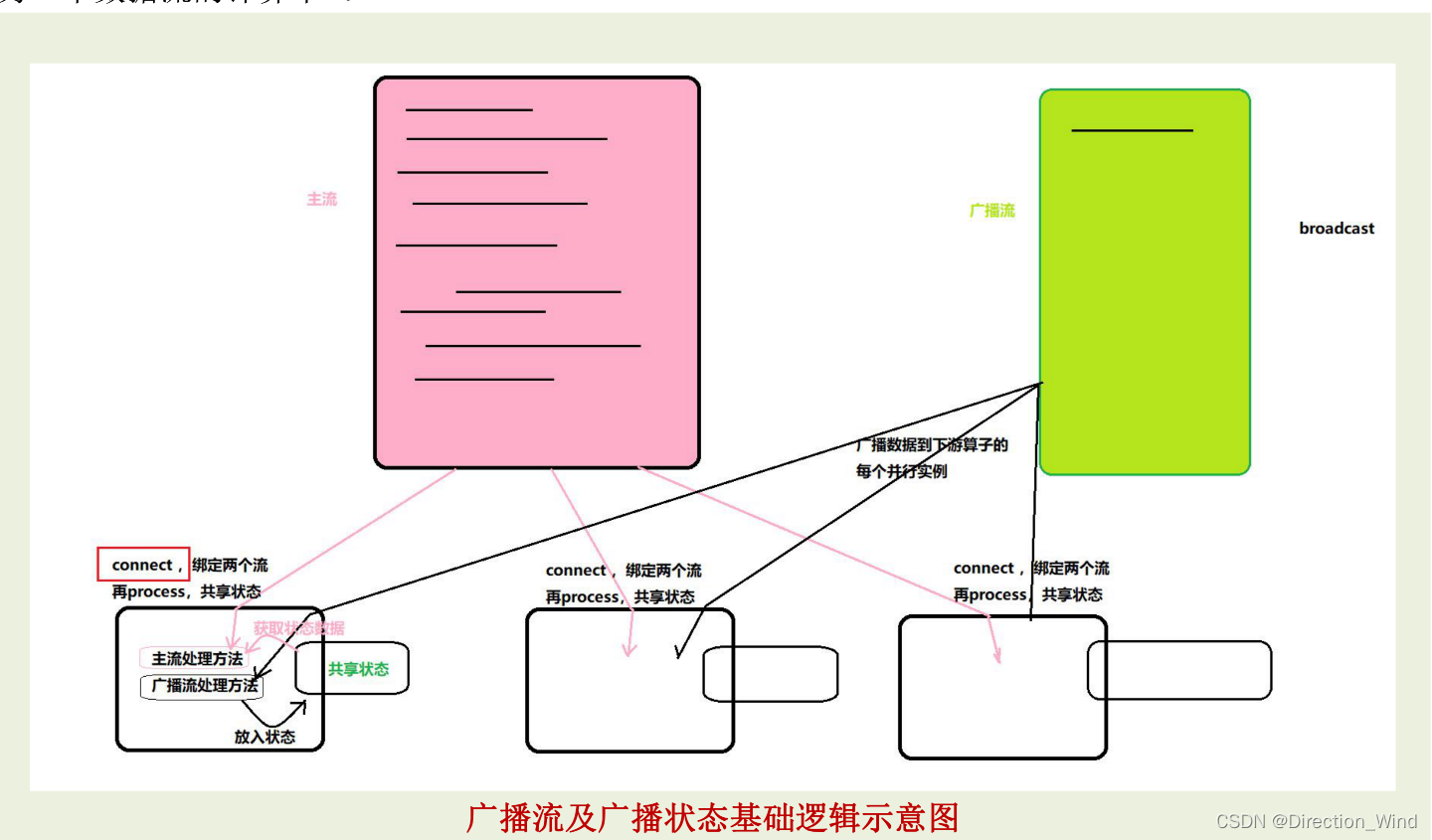
flink多流操作(connect cogroup union broadcast)
flink多流操作1 分流操作2 connect连接操作2.1 connect 连接(DataStream,DataStream→ConnectedStreams)2.2 coMap(ConnectedStreams → DataStream)2.3 coFlatMap(ConnectedStreams → DataStream)3 union操作3.1 uni…...

漫画:什么是快速排序算法?
这篇文章,以对话的方式,详细着讲解了快速排序以及排序排序的一些优化。 一禅:归并排序是一种基于分治思想的排序,处理的时候可以采取递归的方式来处理子问题。我弄个例子吧,好理解点。例如对于这个数组arr[] { 4&…...

vue 3.0组件(下)
文章目录前言:一,透传属性和事件1. 如何“透传属性和事件”2.如何禁止“透传属性和事件”3.多根元素的“透传属性和事件”4. 访问“透传属性和事件”二,插槽1. 什么是插槽2. 具名插槽3. 作用域插槽三,单文件组件CSS功能1. 组件作用…...
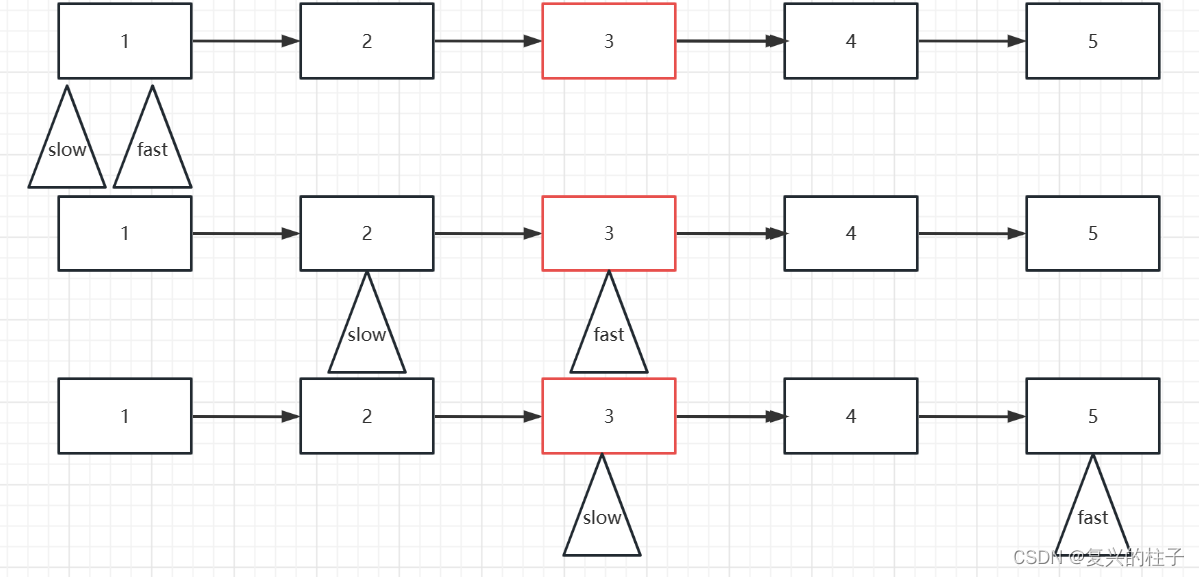
双指针 -876. 链表的中间结点-leetcode
开始一个专栏,写自己的博客 双指针,也算是作为自己的笔记吧! 双指针从广义上来说,是指用两个变量在线性结构上遍历而解决的问题。狭义上说, 对于数组,指两个变量在数组上相向移动解决的问题;对…...

Linux之运行级别
文章目录一、指定运行级别基本介绍CentOS7后运行级别说明一、指定运行级别 基本介绍 运行级别说明: 0:关机 1:单用户【找回丢失密码】 2:多用户状态没有网络服务 3:多用户状态有网络服务 4:系统未使用保留给用户 5:图形界面 6:系统重启 常用运行级别是3和5,也可以…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
