VAE论文阅读
在网上看到的VAE解释,发现有两种版本:
- 按照原来论文中的公式纯数学推导,一般都是了解生成问题的人写的,对小白很不友好。
- 按照实操版本的,非常简单易懂,比如苏神的。但是却忽略了论文中的公式推导,导致论文中公式一点不懂。
下面是我对VAE的理解:
1 VAE生成模型的数学描述
我们见到的生成模型,一般都有这几个步骤:
- 采样一个随机噪声(为啥要随机噪声,因为随机噪声我们是能获得的,调用一个
torch.randn()就可以。) - 输入神经网络一通计算
- 最后输出了图片。
这个过程应该怎么用数学描述呢?在VAE论文中是这样的:

作者的意思是整个模型分为两步:
- 从一个先验分布中采样一个值z,对应之前的第一步
- 从一个后验分布中生成一个值x,对应之前的第二步
模型可以描述为:
p θ ( x ) = ∫ p θ ( z ) p θ ( x ∣ z ) d z p_θ(x) = ∫ p_θ(z)p_θ(x|z) dz pθ(x)=∫pθ(z)pθ(x∣z)dz
这里解释几点:
1. 生成模型为什么是一个概率密度呢,我希望直接有表达式,比如采样了一个噪声z,那么图片 X = g(z),这样多好
其实有了概率密度,可以直接在里面采样。这里是推导过程,大家都这么写。在实际操作的时候,所有的p都会变成一个已知的分布,否则无法计算的。比如假如生成模型的表达式是:
p θ ( x ) = 一些公式 p_\theta(x) = 一些公式 pθ(x)=一些公式
这些公式计算后发现是一个高斯分布 N ( μ , σ ) N(\mu, \sigma) N(μ,σ),那么操作的时候可以写为:
x = μ + σ ε x = \mu + \sigma \varepsilon x=μ+σε
其中 ϵ \epsilon ϵ是随机采样的噪声。所以说,两种形式必须都能看懂才行。
2. 上面的式子含义是什么?
上面的式子中: p θ ( x ) p_\theta(x) pθ(x)是x的概率密度,它的含义是生成模型生成了值为x的样本的概率是多少。
PS 本文中所有的概率都应该是概率密度。但是为了便于理解,就当作概率来写了。
式子的右边是一个全概率公式,意思是计算生成样本x的概率,应该根据生成z的概率,和从z中计算出x的概率计算。
上面的式子其实涵盖了采样+通过采样的z计算x的过程。
2 VAE的损失函数
对生成函数建模后 ,下面考虑如何从z中计算x。下面先说明下实际操作是怎样的,然后结合着理解文中的数学公式。

这里借用了VAE原文中的图。z可以理解为噪声空间,x可以理解为生成的图片空间。这里训练分为两步。
- 首先从样本中获得一个值x,然后通过神经网络计算出对应的z的分布(虚线)
- 从z的分布中采样出一个z
- 根据z重新计算出x(实线)
损失函数包含两项:
- 重建的x和原始的x之间的差值
- z的分布尽可能接近标准正态,因此使用了z的分布和标准正态的KL散度。
使用2的原因是:最终我们需要从标准正态中采样一个z,而不是从样本中计算z,因此让z的分布接近标准正态是为了采样时效果更好。
以上的过程非常符合直觉,遗憾的是这两项是通过数学推导出来的,VAE背景的论文中都会包含数学推导,看懂数学推导的大概意思是必不可少的。下面是推导过程:
VAE损失函数的数学推导
首先VAE模型的目标是最大化似然函数。这里可以理解为:有一个分布中,参数 θ \theta θ是未知的,但是有一组采样结果 x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn是已知的,似然函数表示了采样出这组结果的概率,但是包含了参数 θ \theta θ。通过最大似然函数可以计算出 θ \theta θ的取值。
似然函数的其他内容可以看这篇文章: 文章地址
这里和我们的情况很像:已有的数据可以看成是从一个分布中采样出来的,我们需要求解的是这个分布的参数。
在我们的问题中似然函数可以表示为:
log p θ ( x ( 1 ) , ⋅ ⋅ ⋅ , x ( N ) ) = ∑ i = 1 N log p θ ( x ( i ) ) \log p_θ(x^{(1)}, · · · , x^{(N)}) = \sum^N_{i=1} \log p_θ(x^{(i)}) logpθ(x(1),⋅⋅⋅,x(N))=i=1∑Nlogpθ(x(i))
用更加通俗的话来说就是:模型生成一个数据xi的概率是p(xi), 那么生成出所有数据的概率是p(x1)乘到p(xi)。但是p中有一个参数是未知的,x1到xi是已知的。现在这个参数应该取什么值才能让模型生成出x1到xi的概率最大呢?
求和其实用处不大,下面对某一个数据xi的损失函数进行计算:
log p θ ( x ( i ) ) = D K L ( q φ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ∣ x ( i ) ) ) + L ( θ , φ ; x ( i ) ) \log p_θ(x^{(i)}) = D_{KL}(q_{φ}(z|x^{(i)})||p_{θ}(z|x^{(i)})) + L(θ, φ; x^{(i)}) logpθ(x(i))=DKL(qφ(z∣x(i))∣∣pθ(z∣x(i)))+L(θ,φ;x(i))
其中: L ( θ , φ ; x ( i ) ) = E q φ ( z ∣ x ) [ − log q φ ( z ∣ x ) + log p θ ( x , z ) ] L(θ, φ; x^{(i)}) = E_{q_φ(z|x)} [− \log q_{φ}(z|x) + \log p_θ(x, z)] L(θ,φ;x(i))=Eqφ(z∣x)[−logqφ(z∣x)+logpθ(x,z)]
上面这串到底怎么来的,本来就一个 p θ p_\theta pθ好好的,怎么多了一个 q ϕ q_{\phi} qϕ??
q ϕ q_{\phi} qϕ其实就是encoder,也就是如何把x反向映射到z上。简单来说,整个VAE的训练过程是:
- 在p(z)中采样一个z (采样一个噪声)
- 通过 q ϕ ( z ∣ x ) q_{\phi}(z|x) qϕ(z∣x) 计算出x对应的z
- 通过 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z) 计算出z对应的x
这里 p ( x ∣ y ) p(x|y) p(x∣y)有两种理解方式:
- 给定y之后x的概率是多少
- 给定y之后如何计算x
由于有两个神经网络,所以自然有两个参数。这里p, q其实没什么区别,主要是参数的区别。
OK, 那么上面那个KL散度里面两个分布是怎么回事呢?
其实这个也挺魔幻的,大概就是如果我计算出了 θ \theta θ:
- p θ ( z ) p_{\theta}(z) pθ(z),和 p θ ( x ∣ z ) p_{\theta}(x|z) pθ(x∣z)就都是已知的
- 那么其实 p θ ( z ∣ x ) p_{\theta}(z|x) pθ(z∣x)也是已知的 (根据贝叶斯公式)
- encoder q ϕ ( z ∣ x ) q_{\phi}(z|x) qϕ(z∣x) 同时也描述了这个关系。那么这两个关系应该是接近的
换句话说,我知道了噪声z的分布,同时我有一个样本x,那么我有两种方式计算x对应的z。
- 神经网络decodeer输入z,输出x,再加上贝叶斯公式就能告诉我们应该如何通过x计算z。
- 神经网络encoder输入x,输出z,天然的告诉了我们如何通过x计算z。
这两个过程应该是一致的才行。比如给了一个x, 那么神经网络1+贝叶斯计算的z分布,应该和encoder计算出来的是一样的才行。
好吧,那么似然函数是怎么变成KL散度+ELBO的呢?
推导过程如下:
K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) = ∫ q ϕ ( z ∣ x ) log q ϕ ( z ∣ x ) p θ ( z ∣ x ) d z = ∫ q ϕ ( z ∣ x ) log q ϕ ( z ∣ x ) d z − ∫ q ϕ ( z ∣ x ) log p θ ( z ∣ x ) d z = E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) ] − ∫ q ϕ ( z ∣ x ) log p θ ( z , x ) d z + ∫ q ϕ ( z ∣ x ) log p θ ( x ) d z = E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) ] − E q ϕ ( z ∣ x ) [ log p θ ( z , x ) ] + E q ϕ ( z ∣ x ) log p θ ( x ) = − E L B O + log p θ ( x ) \begin{split} KL(q_{\phi}(z|x)||p_{\theta}(z|x)) &=\displaystyle\int q_{\phi}(z|x)\log\frac{ q_{\phi}(z|x)}{p_{\theta}(z|x)}dz\\ &=\displaystyle\int q_{\phi}(z|x)\log q_{\phi}(z|x)dz-\int q_{\phi}(z|x)\log p_{\theta}(z|x)dz\\ &=\mathbb{E}_{q_{\phi}(z|x)}[\log q_{\phi}(z|x)]-\int q_{\phi}(z|x)\log p_{\theta}(z,x)dz+\int q_{\phi}(z|x)\log p_{\theta}(x)dz\\ &=\mathbb{E}_{q_{\phi}(z|x)}[\log q_{\phi}(z|x)]-\mathbb{E}_{q_{\phi}(z|x)}[\log p_{\theta}(z,x)]+\mathbb{E}_{q_{\phi}(z|x)}\log p_{\theta}(x)\\ &=-ELBO+\log p_{\theta}(x)\\ \end{split} KL(qϕ(z∣x)∣∣pθ(z∣x))=∫qϕ(z∣x)logpθ(z∣x)qϕ(z∣x)dz=∫qϕ(z∣x)logqϕ(z∣x)dz−∫qϕ(z∣x)logpθ(z∣x)dz=Eqϕ(z∣x)[logqϕ(z∣x)]−∫qϕ(z∣x)logpθ(z,x)dz+∫qϕ(z∣x)logpθ(x)dz=Eqϕ(z∣x)[logqϕ(z∣x)]−Eqϕ(z∣x)[logpθ(z,x)]+Eqϕ(z∣x)logpθ(x)=−ELBO+logpθ(x)
经过变换就可以获得似然函数如何表示为KL散度+ELBO的了。
VAE损失函数的数学推导(续)
重写表示了似然函数之后,其实只需要关心ELBO即可,因为KL散度是恒大于0,并且非常难计算,因此最大化似然函数,其实是最大化ELBO罢了。
下面重新改下ELBO:
E L B O = − E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x i ) ] + E q ϕ ( z ∣ x ) [ log p θ ( z , x i ) ] = − E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x i ) ] + E q ϕ ( z ∣ x ) [ log p θ ( z ) p θ ( x i ∣ z ) ] = − E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x i ) ] + E q ϕ ( z ∣ x ) [ log p ( z ) ] + E q ϕ ( z ∣ x ) [ log p θ ( x i ∣ z ) ] = − K L ( q ϕ ( z ∣ x i ) ∣ ∣ p ( z ) ) + E q ϕ ( z ∣ x ) [ log p θ ( x i ∣ z ) ] \begin{array}{rl} ELBO &= -\mathbb{E}_{q_{\phi}(z|x)}[\log q_{\phi}(z|x_i)]+\mathbb{E}_{q_{\phi}(z|x)}[\log p_{\theta}(z,x_i)]\\ &=-\mathbb{E}_{q_{\phi}(z|x)}[\log q_{\phi}(z|x_i)]+\mathbb{E}_{q_{\phi}(z|x)}[\log p_{\theta}(z)p_{\theta}(x_i|z)]\\ &=-\mathbb{E}_{q_{\phi}(z|x)}[\log q_{\phi}(z|x_i)]+\mathbb{E}_{q_{\phi}(z|x)}[\log p(z)]+\mathbb{E}_{q_{\phi}(z|x)}[\log p_{\theta}(x_i|z)]\\ &=-KL(q_{\phi}(z|x_i)||p(z))+\mathbb{E}_{q_{\phi}(z|x)}[\log p_{\theta}(x_i|z)] \end{array} ELBO=−Eqϕ(z∣x)[logqϕ(z∣xi)]+Eqϕ(z∣x)[logpθ(z,xi)]=−Eqϕ(z∣x)[logqϕ(z∣xi)]+Eqϕ(z∣x)[logpθ(z)pθ(xi∣z)]=−Eqϕ(z∣x)[logqϕ(z∣xi)]+Eqϕ(z∣x)[logp(z)]+Eqϕ(z∣x)[logpθ(xi∣z)]=−KL(qϕ(z∣xi)∣∣p(z))+Eqϕ(z∣x)[logpθ(xi∣z)]
可以看出新的ELBO具有两部分,
- 后面一部分可以看作从 x -> q -> z -> x 的过程(这是因为z符合的是q的分布),似然函数需要最大。因此我们最小化了重构损失,这和目标1是一致的。
- 前面一部分可以看作是encoder生成的z必须和z的原始分布相近,在实际中就是encoder通过x计算出的z必须符合正态分布。和我们之前的目标2是一致的
通过不断努力,我们终于从直觉上以及数学上解释了VAE的损失函数构成!
Quiz:
-
在VAE中,重构损失(reconstruction loss)常采用哪种度量方式?
A. 均方误差(MSE)
B. 交叉熵损失
C. Hinge损失
D. Huber损失 -
VAE的主要组成部分有哪些?
A) 编码器和解码器
B) 编码器和分类器
C) 解码器和分类器
D) 编码器和优化器 -
在VAE中,隐变量(latent variable)是从哪个分布中采样的?
A) Bernoulli分布
B) 伽马分布
C) 正态分布
D) 均匀分布 -
VAE通过什么技术来实现隐变量的采样?
A) 反向传播
B) 梯度下降
C) 重参数化技巧(Reparameterization trick)
D) 动量法 -
VAE的目标函数由哪两个主要部分组成?
A) 生成对抗损失和重构损失
B) 重构损失和KL散度
C) 交叉熵损失和KL散度
D) 生成对抗损失和交叉熵损失 -
在VAE中,KL散度(Kullback-Leibler divergence)用于什么?
A) 测量真实数据分布和生成数据分布之间的差异
B) 测量编码器输出和隐变量标准正态分布之间的差异
C) 测量编码器输出和解码器输出之间的差异
D) 测量真实数据分布和隐变量标准正态分布之间的差异 -
在训练VAE的过程中,编码器的输出通常是什么?
A) 一个隐变量的确定值
B) 一个隐变量的分布参数(均值和方差)
C) 一个图像
D) 一个分类标签 -
VAE中的解码器负责什么任务?
A) 将隐变量分布转换为编码器输出
B) 将隐变量样本转换为重构数据
C) 将数据转换为隐变量分布参数
D) 将数据转换为分类标签 -
为什么在VAE中使用重参数化技巧?
A) 为了简化编码器的计算
B) 为了让梯度能够通过随机采样传播
C) 为了提高生成数据的质量
D) 为了减少模型的计算复杂度 -
变分自编码器(VAE)主要用于以下哪种任务?
A. 图像分类
B. 图像生成
C. 文本翻译
D. 语音识别
答案:
- A
- A
- C
- C
- B
- B
- B
- B
- B
- A
相关文章:

VAE论文阅读
在网上看到的VAE解释,发现有两种版本: 按照原来论文中的公式纯数学推导,一般都是了解生成问题的人写的,对小白很不友好。按照实操版本的,非常简单易懂,比如苏神的。但是却忽略了论文中的公式推导ÿ…...

【数据分享】2013-2022年我国省市县三级的逐月SO2数据(excel\shp格式\免费获取)
空气质量数据是在我们日常研究中经常使用的数据!之前我们给大家分享了2000——2022年的省市县三级的逐月PM2.5数据和2013-2022年的省市县三级的逐月CO数据(均可查看之前的文章获悉详情)! 本次我们分享的是我国2013——2022年的省…...

【Jmeter】记录一次Jmeter实战测试
Jmeter实战 1、需求2、实现2.1、新建线程组2.2、导入参数2.3、新建HTTP请求2.4、添加监听器2.5、结果 1、需求 查询某个接口在高并发场景下的响应时间(loadtime),需求需要响应在50ms以内,接下来用Jmeter测试一下 Jmeter安装见文章《Jemeter安装教程&am…...

volatile,最轻量的同步机制
目录 一、volatile 二、如何使用? 三、volatile关键字能代替synchronized关键字吗? 四、总结: 还是老样子,先来看一段代码: 我们先由我们自己的常规思路分析一下代码:子线程中,一直循环&…...

在Linux、Windows和macOS上释放IP地址并重新获取新IP地址的方法
文章目录 LinuxWindowsmacOS 在Linux、Windows和macOS上释放IP地址并重新获取新IP地址的方法各有不同。以下是针对每种操作系统的详细步骤: Linux 使用DHCP客户端:大多数Linux发行版都使用DHCP(动态主机配置协议)来自动获取IP地址…...

Mamba-yolo|结合Mamba注意力机制的视觉检测
一、本文介绍 PDF地址:https://arxiv.org/pdf/2405.16605v1 代码地址:GitHub - LeapLabTHU/MLLA: Official repository of MLLA Demystify Mamba in Vision: A Linear AttentionPerspective一文中引入Baseline Mamba,指明Mamba在处理各种高…...
:自动标识中文多音字)
语音识别标记语言(SSML):自动标识中文多音字
好的,以下是完整的实现代码,包括导入库、分词、获取拼音和生成 SSML 标记的全过程: import thulac from pypinyin import pinyin, Style# 初始化 THULAC thu1 thulac.thulac(seg_onlyTrue)# 测试文本 text "银行行长正在走行。"…...
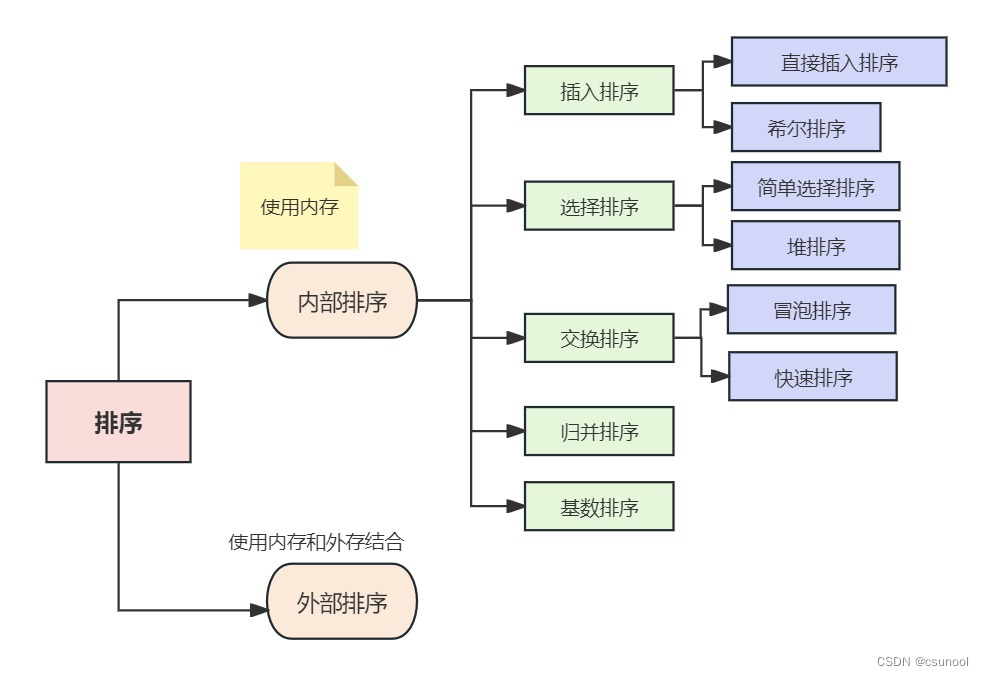
排序算法与复杂度介绍
1. 排序算法 1.1 排序算法介绍 排序也成排序算法(Sort Algorithm),排序是将一组数据,依照指定的顺序进行排序的过程 1.2 排序的分类 1、内部排序: 指将需要处理的所有数据都加载到**内部存储器(内存&am…...
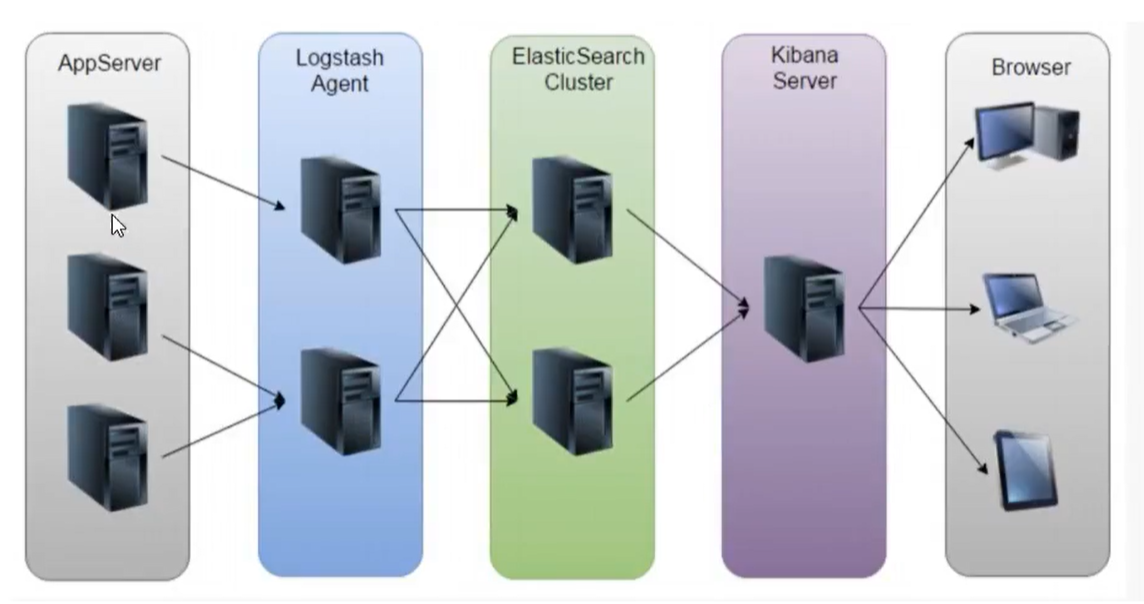
Kafka介绍及Go操作kafka详解
文章目录 Kafka介绍及Go操作kafka详解项目背景解决方案面临的问题业界方案ELKELK方案的问题日志收集系统架构设计架构设计组件介绍将学到的技能消息队列的通信模型点对点模式 queue发布/订阅 topicKafka介绍Kafka的架构图工作流程选择partition的原则ACK应答机制Topic和数据日志…...

DAY05 CSS
文章目录 1 CSS选择器(Selectors)8. 后代(包含)选择器9. 直接子代选择器10. 兄弟选择器11. 相邻兄弟选择器12. 属性选择器 2 伪元素3 CSS样式优先级1. 相同选择器不同样式2. 相同选择器相同样式3. 继承现象4. 选择器不同权值的计算 4 CSS中的值和单位1. 颜色表示法2. 尺寸表示法…...

HTTPS 的加密过程 详解
HTTP 由于是明文传输,所以安全上存在以下三个风险: 窃听风险,比如通信链路上可以获取通信内容。篡改风险,比如通信内容被篡改。冒充风险,比如冒充网站。 HTTPS 在 HTTP 与 TCP 层之间加入了 SSL/TLS 协议,…...

spring整合mybatis,junit纯注解开发(包括连接druid报错的所有解决方法)
目录 Spring整合mybatis开发步骤 第一步:创建我们的数据表 第二步:编写对应的实体类 第三步:在pom.xml中导入我们所需要的坐标 spring所依赖的坐标 mybatis所依赖的坐标 druid数据源坐标 数据库驱动依赖 第四步:编写SpringC…...

ClusterIP、NodePort、LoadBalancer 和 ExternalName
Service 定义 在 Kubernetes 中,由于Pod 是有生命周期的,如果 Pod 重启它的 IP 可能会发生变化以及升级的时候会重建 Pod,我们需要 Service 服务去动态的关联这些 Pod 的 IP 和端口,从而使我们前端用户访问不受后端变更的干扰。 …...

【Day1415】Bean管理、SpringBoot 原理、总结、Maven 高级
0 SpringBoot 配置优先级 从上到下 虽然 springboot 支持多种格式配置文件,但是在项目开发时,推荐统一使用一种格式的配置 (yml是主流) 1 Bean管理 1.1 从 IOC 容器中获取 Bean 1.2 Bean 作品域 可以通过注解 Scope("proto…...

Git之repo sync -c与repo sync -dc用法区别(四十八)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

vite + vue3 + uniapp 项目从零搭建
vite + vue3 + uniapp 项目从零搭建 1、创建项目1.1、创建Vue3/vite版Uniapp项目1.2、安装依赖1.3、运行项目2、弹出 用户隐私保护提示 方法2.1、更新用户隐私保护指引 和 修改配置文件2.2、授权结果处理方法3、修改`App.vue`文件内容4、处理报`[plugin:uni:mp-using-component…...

在CentOS中配置三个节点之间相互SSH免密登陆
在CentOS中配置三个节点(假设分别为node1、node2、node3)两两之间相互SSH免密登陆,可以按照以下步骤进行: 一、生成密钥对 在所有节点上生成密钥对: 在每个节点(node1、node2、node3)上执行以…...

arm 内联汇编基础
一、 Arm架构寄存器体系熟悉 基于arm neon 实现的代码有 intrinsic 和inline assembly 两种实现。 1.1 通用寄存器 arm v7 有 16 个 32-bit 通用寄存器,用 r0-r15 表示。 arm v8 有 31 个 64-bit 通用寄存器,用 x0-x30 表示,和 v7 不一样…...

Java语言程序设计——篇五(1)
数组 概述数组定义实例展示实战演练 二维数组定义数组元素的使用数组初始化器实战演练:矩阵计算 💫不规则二维数组实战演练:杨辉三角形 概述 ⚡️数组是相同数据类型的元素集合。各元素是有先后顺序的,它们在内存中按照这个先后顺…...

【香橙派开发板测试】:在黑科技Orange Pi AIpro部署YOLOv8深度学习纤维分割检测模型
文章目录 🚀🚀🚀前言一、1️⃣ Orange Pi AIpro开发板相关介绍1.1 🎓 核心配置1.2 ✨开发板接口详情图1.3 ⭐️开箱展示 二、2️⃣配置开发板详细教程2.1 🎓 烧录镜像系统2.2 ✨配置网络2.3 ⭐️使用SSH连接主板 三、…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
