Python鲁汶意外莱顿复杂图拓扑分解算法
🎯要点
🎯算法池化和最佳分区搜索:🖊网格搜索 | 🖊发现算法池 | 🖊返回指定图的最佳划分 | 🖊返回指定图的最佳分区 | 🎯适应度和聚类比较功能:🖊图的划分 | 🖊节点度 | 🖊给定算法检测到社群总数 | 🖊图密度 | 🖊社群顶点的度数之和 | 🖊解之间的预期一致 | 🖊联合熵 | 🖊平均内部度、所有可能的节点对的平均路径长度 | 🖊节点指向社群外的边平均比例 | 🖊现有边距离社群比例 | 社群内部密度 | 🖊切割比率的标准化变体 | 🖊边超几何分布随机出现的统计方法 | 🖊兰德指数预测聚类之间的相似性度量 | 分区之间最佳匹配的平均 F1 分数 | 归一化互信息
📜图算法用例
📜Python群体趋向性潜关联有向无向多图层算法
📜Python和MATLAB网络尺度结构和幂律度大型图生成式模型算法
📜MATLAB和Python零模型社会生物生成式结构化图
📜Python莫兰生死抑制放大进化图
📜Python种群邻接矩阵彗星风筝进化图算法
📜Python和C++骨髓细胞进化解析数学模型
🍪语言内容分比


🍇Python和MATLAB异构网络算法
异构信息网络是一种网络结构,其对象可以假设不同的对象类型,对象之间的链接可以表示对象之间的不同类型的关系。此网无处不在,用于对许多不同类型的现实世界数据进行建模。例如,社交软件开放图将用户、帖子、事件和页面建模为四种不同类型的对象。用户可以发布帖子、参加活动或喜欢页面,这说明了将用户对象与帖子相关联的三种不同类型的连接。
此网络数据分析一直是一个活跃的研究领域。作为机器学习和数据挖掘的一项基本任务,聚类分析在此网络中找到了有趣的应用。例如,根据社交软件用户的兴趣对其进行聚类,可以实现有效的目标营销和病毒式营销。
谱聚类将聚类转化为图分割问题,该问题优化衡量分割质量的某个标准,例如正则化切割。通常,给定一组对象 X = { x 1 , x 2 , … , x n } X=\left\{x_1, x_2, \ldots, x_n\right\} X={x1,x2,…,xn},标准谱聚类方法首先构造一个无向图 G = ( X , S ) G=(X, S) G=(X,S),其中 X X X 表示顶点集, S S S 是一个矩阵, S i j S_{i j} Sij 度量对象 x i x_i xi 和 x j x_j xj 之间的相似性。然后,计算拉普拉斯矩阵 L S L_S LS,在此基础上执行特征分解以获得与 k k k 个最小特征值相对应的 k k k 个特征向量,其中 k k k 是所需的聚类数量。这些特征向量被用作对象的新特征空间。最后,应用后处理步骤,例如 k k k 均值和光谱旋转将对象划分为 k k k 个聚类。
异构信息网络:
令 T = { T 1 , … , T m } T =\left\{T_1, \ldots, T_m\right\} T={T1,…,Tm} 为一组 m m m 对象类型。对于每种类型 T i T_i Ti,令 X i X _i Xi 为类型 T i T_i Ti 的对象集。 异构信息网络是一个图 G = ( V , E ) G =( V , E ) G=(V,E),其中 V = ⋃ i = 1 m X i V =\bigcup_{i=1}^m X _i V=⋃i=1mXi 是一组节点, E E E 是一组链接,每个链接代表一个二进制 V V V 中两个对象之间的关系。
它的网络模式:

网络模式是异构信息网络 G = ( V , E ) G =( V , E ) G=(V,E) 的元模板。令 (1) ϕ : V → T \phi: V \rightarrow T ϕ:V→T 为对象类型映射,将 V V V 中的对象映射为其类型,(2) ψ : E → R \psi: E \rightarrow R ψ:E→R 为链接关系映射将 E E E 中的链接映射到一组关系 R R R 中的关系。异构信息网络 G G G 的网络模式用 T G = ( T , R ) T_{ G }=( T , R ) TG=(T,R) 表示,显示了不同类型的对象如何通过 R R R 中的关系进行关联。使用示意图来表示 T G T_{G} TG,其中 T T T和 R R R分别为节点集和边集。具体来说,示意图中存在一条边 ( T i , T j ) \left(T_i, T_j\right) (Ti,Tj) ,前提是 R R R 中存在将 T i T_i Ti 类型的对象与 T j T_j Tj 类型的对象相关联的关系。
算法
谱聚类的关键步骤是构建高质量的相似度矩阵 S S S。对于异构信息网络,元路径已被有效地用于测量对象相似性。例如,给定元路径 P P P,PathSim测量两个对象 x u x_u xu 和 x v x_v xv 之间的相似度。 P P P 通过计算连接两个对象的 P P P 的路径实例的数量。具体来说,我们有,
S P ( x u , x v ) = 2 × ∣ { p x u ⇝ x v : p x u ⇝ x v ⊢ P } ∣ ∣ { p x u ⇝ x u : p x u → x u ⊢ P } ∣ + ∣ { p x v ⇝ x v : p x v ⇝ x v ⊢ P } ∣ . S_{ P }\left(x_u, x_v\right)=\frac{2 \times\left|\left\{p_{x_u \rightsquigarrow x_v}: p_{x_u \rightsquigarrow x_v} \vdash P \right\}\right|}{\left|\left\{p_{x_u \rightsquigarrow x_u}: p_{x_u \rightarrow x_u} \vdash P \right\}\right|+\left|\left\{p_{x_v \rightsquigarrow x_v}: p_{x_v \rightsquigarrow x_v} \vdash P \right\}\right|} . SP(xu,xv)=∣{pxu⇝xu:pxu→xu⊢P}∣+∣{pxv⇝xv:pxv⇝xv⊢P}∣2×∣{pxu⇝xv:pxu⇝xv⊢P}∣.
给定一组元路径 P S P S PS,每个元路径 P i ∈ P S P _i \in P S Pi∈PS 根据上式导出相似性矩阵 S P i S_{ P _i} SPi。我们构造一个矩阵 W W W 作为以下各项的加权和:矩阵:
W = ∑ i = 1 ∣ P S ∣ λ i S P i . W=\sum_{i=1}^{| P S |} \lambda_i S_{ P _i} . W=i=1∑∣PS∣λiSPi.
优化
由于约束 rank ( L S ) = n − k \operatorname{rank}\left(L_S\right)=n-k rank(LS)=n−k,优化问题是非凸的。因此很难直接优化问题。我们将原问题转化为:
min ∥ S − ∑ i = 1 ∣ P S ∣ λ i S P i ∥ F 2 + α ∥ S ∥ F 2 + β ∥ λ ∥ 2 2 + 2 γ ∑ i = 1 k σ i ( L S ) , s.t. ∑ j = 1 n S i j = 1 , S i j ≥ 0 , ∑ i = 1 ∣ P S ∣ λ i = 1 , λ i ≥ 0 , \begin{aligned} & \min \left\|S-\sum_{i=1}^{| P S |} \lambda_i S_{ P _i}\right\|_F^2+\alpha\|S\|_F^2+\beta\| \lambda \|_2^2+2 \gamma \sum_{i=1}^k \sigma_i\left(L_S\right), \\ & \text { s.t. } \sum_{j=1}^n S_{i j}=1, S_{i j} \geq 0, \sum_{i=1}^{| P S |} \lambda_i=1, \lambda_i \geq 0, \end{aligned} min S−i=1∑∣PS∣λiSPi F2+α∥S∥F2+β∥λ∥22+2γi=1∑kσi(LS), s.t. j=1∑nSij=1,Sij≥0,i=1∑∣PS∣λi=1,λi≥0,
其中 σ i ( L S ) \sigma_i\left(L_S\right) σi(LS)表示 L S L_S LS的第 i i i个最小特征值。由于 L S L_S LS是半定的, σ i ( L S ) ≥ 0 \sigma_i\left(L_S\right)\geq 0 σi(LS)≥0。通过设置较大的 γ \gamma γ 值,我们将 ∑ i = 1 k σ i ( L S ) \sum_{i=1}^k \sigma_i\left(L_S\right) ∑i=1kσi(LS) 强制为零,以保证 rank ( L S ) ) = n − k \operatorname{rank}\left(L_S\right) )=n-k rank(LS))=n−k。根据凯-范定理,我们有,
∑ i = 1 k σ i ( L S ) = min F ∈ R n × k , F T F = I tr ( F T L S F ) \sum_{i=1}^k \sigma_i\left(L_S\right)=\min _{F \in R ^{n \times k}, F^T F=I} \operatorname{tr}\left(F^T L_S F\right) i=1∑kσi(LS)=F∈Rn×k,FTF=Imintr(FTLSF)
其中 tr ( ⋅ ) \operatorname{tr}(\cdot) tr(⋅) 是跟踪运算符。因此优化问题等价于:
min ∥ S − ∑ i = 1 ∣ P S ∣ λ i S P i ∥ F 2 + α ∥ S ∥ F 2 + β ∥ λ ∥ 2 2 + 2 γ tr ( F T L S F ) , s.t. ∑ j = 1 n S i j = 1 , S i j ≥ 0 , ∑ i = 1 ∣ P S ∣ λ i = 1 , λ i ≥ 0 , F ∈ R n × k , F T F = I , \begin{aligned} & \min \left\|S-\sum_{i=1}^{| P S |} \lambda_i S_{ P _i}\right\|_F^2+\alpha\|S\|_F^2+\beta\| \lambda \|_2^2+2 \gamma \operatorname{tr}\left(F^T L_S F\right), \\ & \text { s.t. } \sum_{j=1}^n S_{i j}=1, S_{i j} \geq 0, \sum_{i=1}^{| P S |} \lambda_i=1, \lambda_i \geq 0, F \in R ^{n \times k}, F^T F=I, \end{aligned} min S−i=1∑∣PS∣λiSPi F2+α∥S∥F2+β∥λ∥22+2γtr(FTLSF), s.t. j=1∑nSij=1,Sij≥0,i=1∑∣PS∣λi=1,λi≥0,F∈Rn×k,FTF=I,
Python伪代码实现算法:
from sklearn.cluster import KMeans
import numpy as np
from scipy.optimize import minimizeclass alg:def __init__(self, similarity_matrices, num_clusters, random_seed=0):self.num_clusters = num_clustersself.random_seed = random_seedself.num_nodes = Noneself.similarity_matrices = []self.metapath_index = {}self.alpha = Noneself.beta = Noneself.gamma = Nonefor index, (metapath, matrix) in enumerate(similarity_matrices.items()):if self.num_nodes is None:self.num_nodes = matrix.shape[0]if matrix.shape != (self.num_nodes, self.num_nodes):raise ValueError('Invalid shape of similarity matrix.')row_normalized_matrix = matrix/matrix.sum(axis=1, keepdims=True)self.similarity_matrices.append(row_normalized_matrix)self.metapath_index[metapath] = indexself.similarity_matrices = np.array(self.similarity_matrices)self.num_metapaths = len(similarity_matrices)def run(self, verbose=False, cluster_using='similarity'):if cluster_using not in ['similarity', 'laplacian']:raise ValueError('Invalid option for parameter \'cluster_using\'.')similarity_matrix, metapath_weights = self.optimize(verbose=verbose)if cluster_using == 'similarity':labels = self.cluster(similarity_matrix)elif cluster_using == 'laplacian':laplacian = normalized_laplacian(similarity_matrix)labels = self.cluster(eigenvectors(laplacian, num=self.num_clusters))metapath_weights_dict = {metapath: metapath_weights[index] for metapath, index in self.metapath_index.items()}return labels, similarity_matrix, metapath_weights_dictdef cluster(self, feature_matrix):return KMeans(self.num_clusters, n_init=10, random_state=self.random_seed).fit_predict(feature_matrix)def optimize(self, num_iterations=20, alpha=0.5, beta=10, gamma=0.01, verbose=False):self.alpha = alphaself.beta = betaself.gamma = gammalambdas = np.ones(self.num_metapaths)/self.num_metapathsW = np.tensordot(lambdas, self.similarity_matrices, axes=[[0], [0]])S = Wfor iteration in range(num_iterations):if verbose:loss = np.trace(np.matmul((S - W).T, (S - W))) loss += self.alpha * np.trace(np.matmul(S.T, S))loss += self.beta * np.dot(lambdas, lambdas)loss += self.gamma * np.sum(eigenvalues(normalized_laplacian(S), num=self.num_clusters))print('Iteration %d: Loss = %0.3f' % (iteration, loss))F = self.optimize_F(S)S = self.optimize_S(W, F)lambdas = self.optimize_lambdas(S, lambdas)W = np.tensordot(lambdas, self.similarity_matrices, axes=[[0], [0]])return S, lambdasdef optimize_F(self, S):LS = normalized_laplacian(S) return eigenvectors(LS, num=self.num_clusters)def optimize_S(self, W, F):Q = distance_matrix(F, metric='euclidean')P = (2*W - self.gamma*Q)/(2 + 2*self.alpha)S = np.zeros((self.num_nodes, self.num_nodes)) for index in range(S.shape[0]):S[index] = best_simplex_projection(P[index])return Sdef optimize_lambdas(self, S, init_lambdas):def objective(lambdas):W = np.tensordot(lambdas, self.similarity_matrices, axes=[[0], [0]])value = np.trace(np.matmul(W.T, W))value -= 2 * np.trace(np.matmul(S.T, W))value += self.beta * np.dot(lambdas, lambdas)return valuedef constraints():def sum_one(lambdas):return np.sum(lambdas) - 1return {'type': 'eq','fun': sum_one,}def bounds(init_lambdas):return [(0, 1) for init_lambda in init_lambdas]return minimize(objective, init_lambdas, method='SLSQP', constraints=constraints(), bounds=bounds(init_lambdas)).xMATLAB伪代码算法实现:
function [y, S, evs, A] = alg(mp_matrix, c, true_cluster)NITER = 20;
zr = 10e-11;alpha = 0.5;
beta = 10;
gamma = 0.01; P = size(mp_matrix,1);
n = size(mp_matrix,2);
lambda = ones(P,1)./P;eps = 1e-10;
A0 = zeros(n,n);
for p = 1:PA0 = A0 + lambda(p) * squeeze(mp_matrix(p,:,:));
end;A0 = A0-diag(diag(A0));
A10 = (A0+A0')/2;
D10 = diag(sum(A10));
L0 = D10 - A10;[F0, ~, evs]=eig1(L0, n, 0);
F = F0(:,1:c);
[pred] = postprocess(F,c,true_cluster);for iter = 1:NITERdist = L2_distance_1(F',F');S = zeros(n);for i=1:na0 = A0(i,:);idxa0 = 1:n;ai = a0(idxa0);di = dist(i,idxa0);ad = (ai-0.5*gamma*di)/(1+alpha); S(i,idxa0) = EProjSimplex_new(ad);end;A = S;A = (A+A')/2;D = diag(sum(A));L = D-A;F_old = F;[F, ~, ev]=eig1(L, c, 0);[pred] = postprocess(F,c,true_cluster);evs(:,iter+1) = ev;fn1 = sum(ev(1:c));fn2 = sum(ev(1:c+1));lambda_old = lambda;if fn1 > zrgamma = 2*gamma;lambda = optimizeLambda(mp_matrix, S, beta); % optimize lambdaelseif fn2 < zrgamma = gamma/2; F = F_old; lambda = lambda_old;elsebreak;end;A0 = zeros(n,n);for p = 1:PA0 = A0 + lambda(p) * squeeze(mp_matrix(p,:,:));end;end;[clusternum, y]=graphconncomp(sparse(A)); y = y';
nmi = calculateNMI(y,true_cluster);
purity = eval_acc_purity(true_cluster,y);
ri = eval_rand(true_cluster,y);fprintf('Final NMI is %f\n',nmi);
fprintf('Final purity is %f\n',purity);
fprintf('Final rand is %f\n',ri);if clusternum ~= csprintf('Can not find the correct cluster number: %d', c)
end;
👉参阅、更新:计算思维 | 亚图跨际
相关文章:

Python鲁汶意外莱顿复杂图拓扑分解算法
🎯要点 🎯算法池化和最佳分区搜索:🖊网格搜索 | 🖊发现算法池 | 🖊返回指定图的最佳划分 | 🖊返回指定图的最佳分区 | 🎯适应度和聚类比较功能:🖊图的划分 |…...

【C++】类和对象之继承
目录 继承的概念和定义 继承的概念 继承的定义 继承的定义格式 继承关系和访问限定符 继承基类成员访问方式的变化 访问权限实例 基类和派生类对象赋值转换 继承中的作用域 派生类的默认成员函数 继承与友元 继承与静态成员 复杂的菱形继承及菱形虚拟继承 继承的…...

如何在LlamaIndex中使用RAG?
如何在LlamaIndex中使用RAG 什么是 Llama-Index LlamaIndex 是一个数据框架,用于帮助基于 LLM 的应用程序摄取、构建结构和访问私有或特定领域的数据。 如何使用 Llama-Index ? 基本用法是一个五步流程,将我们从原始、非结构化数据导向基于该数据生成…...
css气泡背景特效
css气泡背景特效https://www.bootstrapmb.com/item/14879 要创建一个CSS气泡背景特效,你可以使用CSS的伪元素(:before 和 :after)、border-radius 属性来创建圆形或椭圆形的“气泡”,以及background 和 animation 属性来设置背景…...

7.23模拟赛总结 [数据结构优化dp] + [神奇建图]
目录 复盘题解T2T4 复盘 浅复盘下吧… 7:40 开题 看 T1 ,起初以为和以前某道题有点像,子序列划分,注意到状态数很少,搜出来所有状态然后 dp,然后发现这个 T1 和那个毛关系没有 浏览了一下,感觉 T2 题面…...

MySQL-视 图
视 图 创建视图 视图是从一个或者几个基本表(或视图)导出的表。它与基 本表不同,是一个虚表。 语法: create view 视图名 【view_xxx/v_xxx】 说明: • view_name 自己定义的视图名; • as 后面是这…...

PHP SimpleXML
PHP SimpleXML PHP的SimpleXML扩展提供了一个非常方便的方式来处理XML数据。它是PHP内置的,因此不需要安装额外的库。SimpleXML可以将XML数据转换成对象,使得操作XML变得简单直观。本文将详细介绍SimpleXML的使用方法,包括加载XML、访问和修…...

【Spring Boot 自定义配置项详解】
文章目录 一、配置文件1. properties配置1.1 创建配置文件1.2 添加配置项1.3 在应用中使用配置项1.4 多环境配置 2. YAML配置2.1 创建配置文件2.2 添加配置项2.3 在应用中使用配置项2.4 多环境配置 二、自定义配置类1. 创建配置类2. 使用配置类 一、配置文件 Spring Boot支持多…...
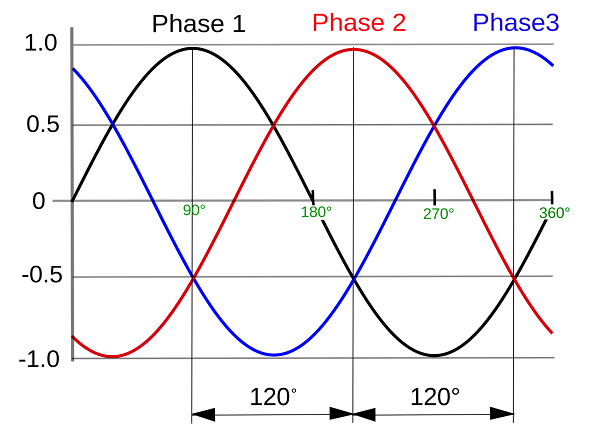
电机相位接线错误导致的潜在问题
交流电机有两种基本类型:单相和三相。一般来说,单相交流电机通常用于家用电器等住宅应用,而三相交流电机则用于工业应用。这主要是因为大多数家庭使用单相电源,而大多数工业场所使用三相电源。 鉴于这两种不同的电源方案…...

react中如何mock数据
1.需求说明 因为前后端分离开发项目,就会存在前端静态页面写好了,后端数据接口还没写好;这时候前端就需要自己定义数据来使用。 定义数据有三种方式:直接写死数据、使用mock软件、json-server工具 这里讲解通过json-server工具…...

通过Faiss和DINOv2进行场景识别
目标:通过Faiss和DINOv2进行场景识别,确保输入的照片和注册的图片,保持内容一致。 MetaAI 通过开源 DINOv2,在计算机视觉领域取得了一个显着的里程碑,这是一个在包含1.42 亿张图像的令人印象深刻的数据集上训练的模型…...

新手入门基础Java
一:基础语法 1.Java的运行机制 2. Java基本语法 1.注释、标识符、关键字; 2.数据类型(四类八种) 3.类型转换 1.自动转换;2.强制转换; 4.常量和变量 1.常量;2.变量; 3.变量的作用域 5.运算符 1.算数运算符;2.赋值运算符;3.关系运算符; 4.逻辑运算符;5.自…...

2024最新版虚拟便携空调小程序源码 支持流量主切换空调型号
产品截图 部分源代码展示 urls.js Object.defineProperty(exports, "__esModule", {value: !0 }), exports.default ["9c5f1fa582bee88300ffb7e28dce8b68_3188_128_128.png", "E-116154b04e91de689fb1c4ae99266dff_960.svg", "573eee719…...

前端在浏览器总报错,且获取请求头中token的值为null
前端请求总是失败说受跨域请求影响,但前后端配置已经没有问题了,如下: package com.example.shop_manage_sys.config;import org.springframework.beans.factory.annotation.Autowired; import org.springframework.context.annotation.Conf…...

html+css前端作业 王者荣耀官网6个页面无js
htmlcss前端作业 王者荣耀官网6个页面无js 下载地址 https://download.csdn.net/download/qq_42431718/89571150 目录1 目录2 项目视频 王者荣耀6个页面(无js) 页面1 页面2 页面3 页面4 页面5 页面6...

在windows上使用Docker部署一个简易的web程序
使用Docker部署一个python的web服务🚀 由于是从事算法相关工作,之前在项目中,需要将写完的代码服务,部署在docker上,以此是开始接触了Docker这个工具,由于之前也没系统学习过,之后应该可能还会用…...

sqlalchemy使用mysql的json_extract函数查询JSON字段
sqlalchemy使用mysql的json_extract函数查询JSON字段 在SQLAlchemy中,如果你想要在MySQL中存储JSON字段,并且进行查询操作,可以按照以下步骤进行设置和查询: 1. 创建表格 首先,创建一个表格来存储包含JSON字段的数据。假设我们有一个名为 users 的表格,其中有一个名为…...

分类模型-逻辑回归和Fisher线性判别分析★★★★
该博客为个人学习清风建模的学习笔记,部分课程可以在B站:【强烈推荐】清风:数学建模算法、编程和写作培训的视频课程以及Matlab等软件教学_哔哩哔哩_bilibili 目录 1理论 1.1逻辑回归模型 1.2线性概率模型 1.3线性判别分析 1.4两点分布…...
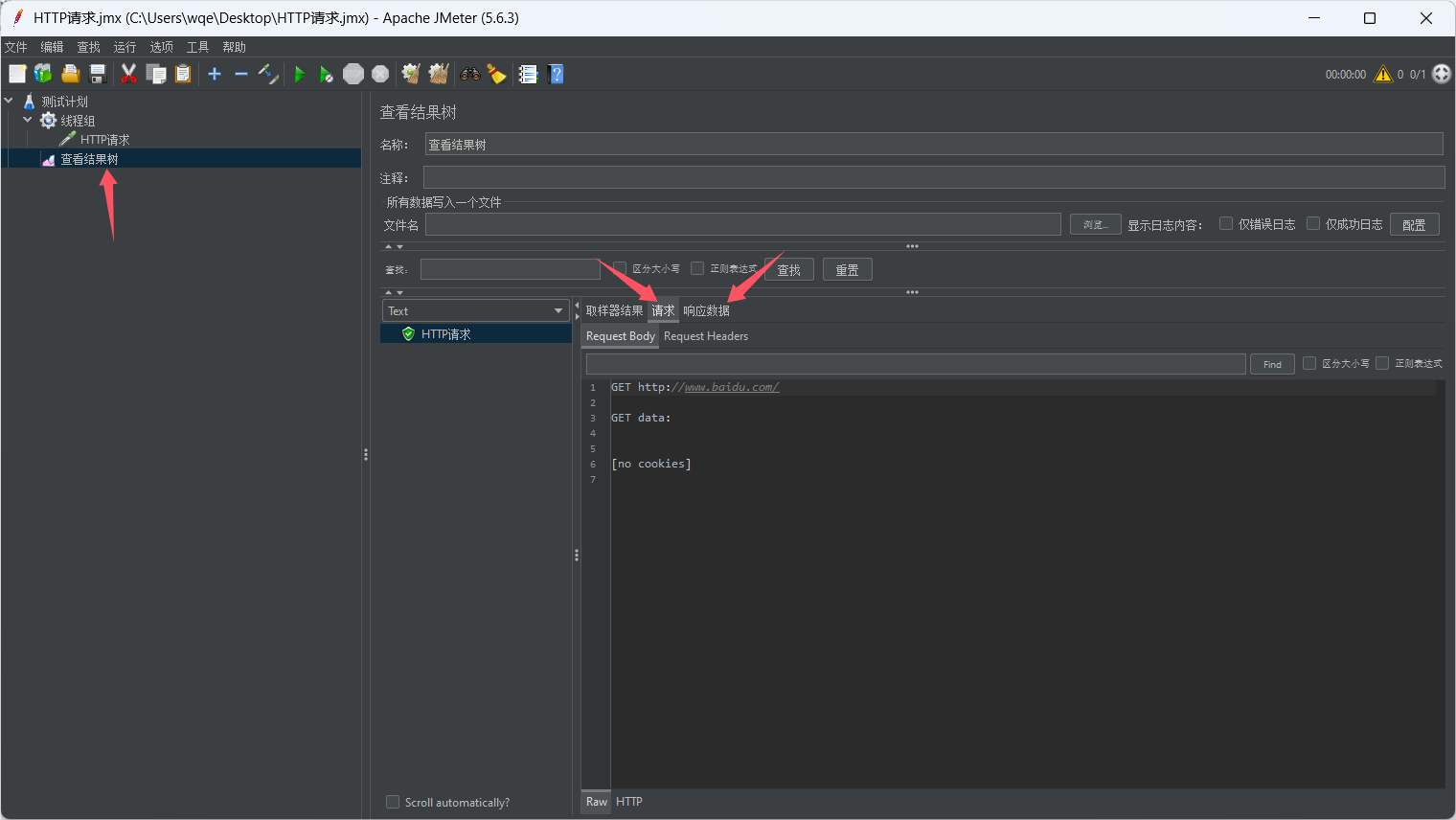
JMeter介绍、安装配置以及快速入门
文章目录 1. JMeter简介2. JMeter安装配置3. JMeter快速入门 1. JMeter简介 Apache JMeter是一款开源的压力测试工具,主要用于测试静态和动态资源(如静态文件、服务器、数据库、FTP服务器等)的性能。它最初是为测试Web应用而设计的ÿ…...

GPT LangChain experimental agent - allow dangerous code
题意:GPT LangChain 实验性代理 - 允许危险代码 问题背景: Im creating a chatbot in VS Code where it will receive csv file through a prompt on Streamlit interface. However from the moment that file is loaded, it is showing a message with…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
