C语言刷题(7)(字符串旋转问题)——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容依旧是复习之前的知识点,那么,就是做一道小小的题目啦,下面,让我们进入C语言的世界吧
实现一个函数,可以左旋字符串中的k个字符。
例如:
ABCD左旋一个字符得到BCDA
ABCD左旋两个字符得到CDAB
首先,给定一个字符串
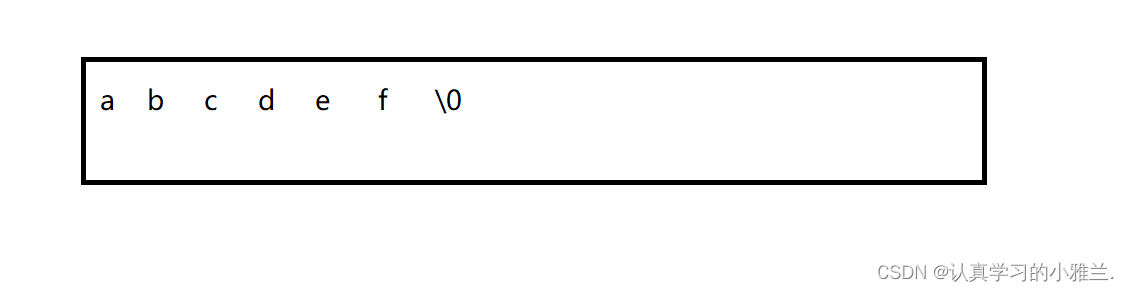
如果是左旋一个字符,那么可以这样来做:把a拿出来,放在自己定义的一个变量中,再把b移到原来a的位置,以此类推,把c移到原先b的位置,把d移到原先c的位置,把e移到原先d的位置,把f移到原先e的位置,最后,把a放到原先f的位置,这样,就成功左旋一个字符啦
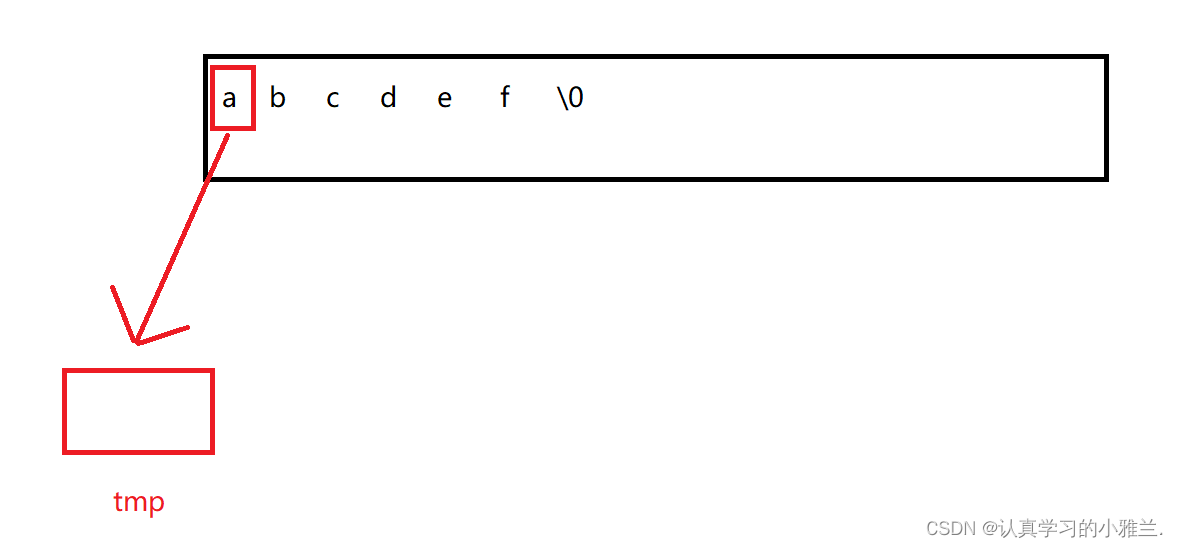

好啦,基本思路就是这个样子,然后,我们来写代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<string.h>
void left_move(char arr[], int k)
{int i = 0;int len = strlen(arr);k = k % len;for (i = 0; i < k; i++){//左旋一个字符//1char tmp = arr[0];//2int j = 0;for (j = 0; j < len - 1; j++){arr[j] = arr[j + 1];}//3arr[len - 1] = tmp;}
}
int main()
{char arr[20] = "abcdef";int k = 0;scanf("%d", &k);left_move(arr, k);printf("%s\n", arr);return 0;
} 
另一种方法——三步翻转法
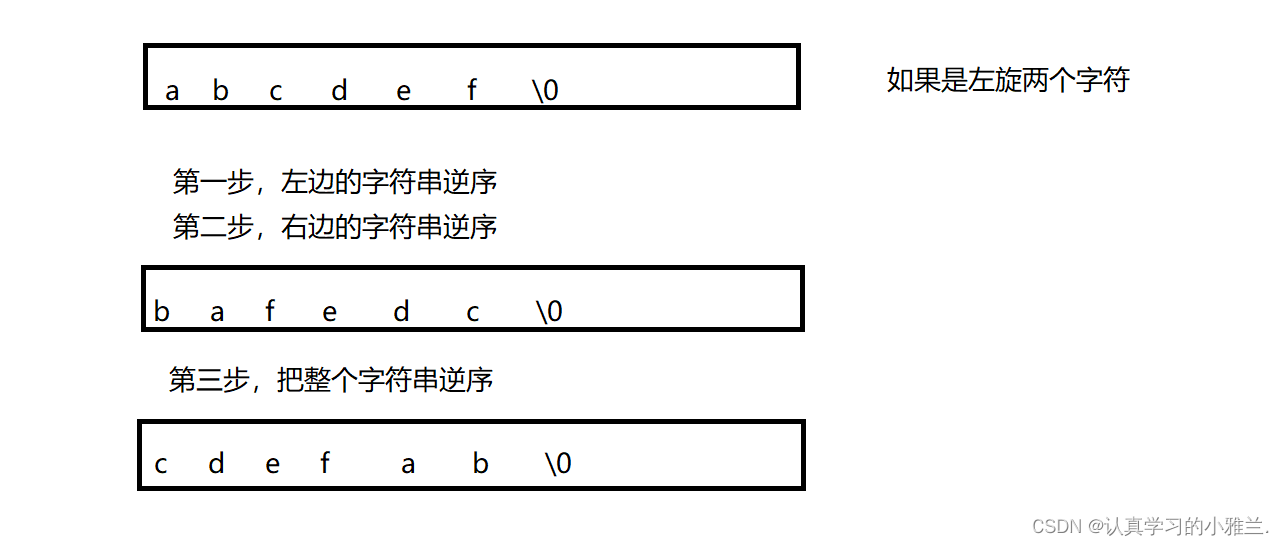
然后,肯定需要用到字符串逆序的函数,字符串逆序,就是:把b和c交换顺序,a和d交换顺序,f和e交换顺序
#include<stdio.h>
#include<string.h>
#include<assert.h>
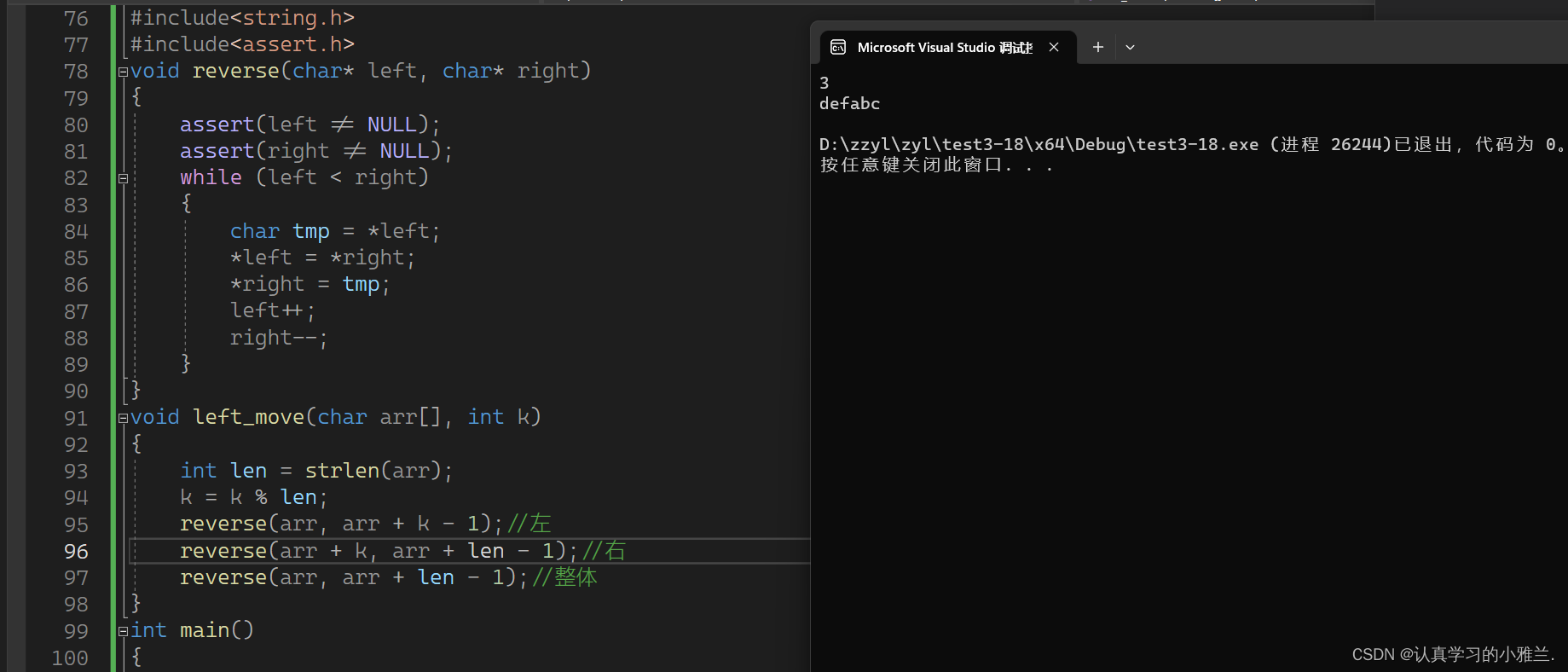
void reverse(char* left, char* right)
{assert(left != NULL);assert(right != NULL);while (left < right){char tmp = *left;*left = *right;*right = tmp;left++;right--;}
}
void left_move(char arr[], int k)
{int len = strlen(arr);k = k % len;reverse(arr, arr + k - 1);//左reverse(arr + k, arr + len - 1);//右reverse(arr, arr + len - 1);//整体
}
int main()
{char arr[20] = "abcdef";int k = 0;scanf("%d", &k);left_move(arr, k);printf("%s\n", arr);return 0;
} 
写一个函数,判断一个字符串是否为另外一个字符串旋转之后的字符串。
例如:
给定s1 =AABCD和s2 = BCDAA,返回1
给定s1=abcd和s2=ACBD,返回0.
AABCD左旋一个字符得到ABCDA
AABCD左旋两个字符得到BCDAA
AABCD右旋一个字符得到DAABC
和上面的题目非常相似
#include<stdio.h>
#include<string.h>
int is_left_move(char arr1[], char arr2[])
{int i = 0;int len = strlen(arr1);for (i = 0; i < len; i++){//左旋一个字符//1char tmp = arr1[0];//2int j = 0;for (j = 0; j < len - 1; j++){arr1[j] = arr1[j + 1];}//3arr1[len - 1] = tmp;if (strcmp(arr1, arr2) == 0){return 1;}}return 0;
}
int main()
{char arr1[] = "abcdef";char arr2[] = "cdefab";int ret = is_left_move(arr1, arr2);if (ret == 1){printf("yes\n");}else{printf("no\n");}return 0;
}
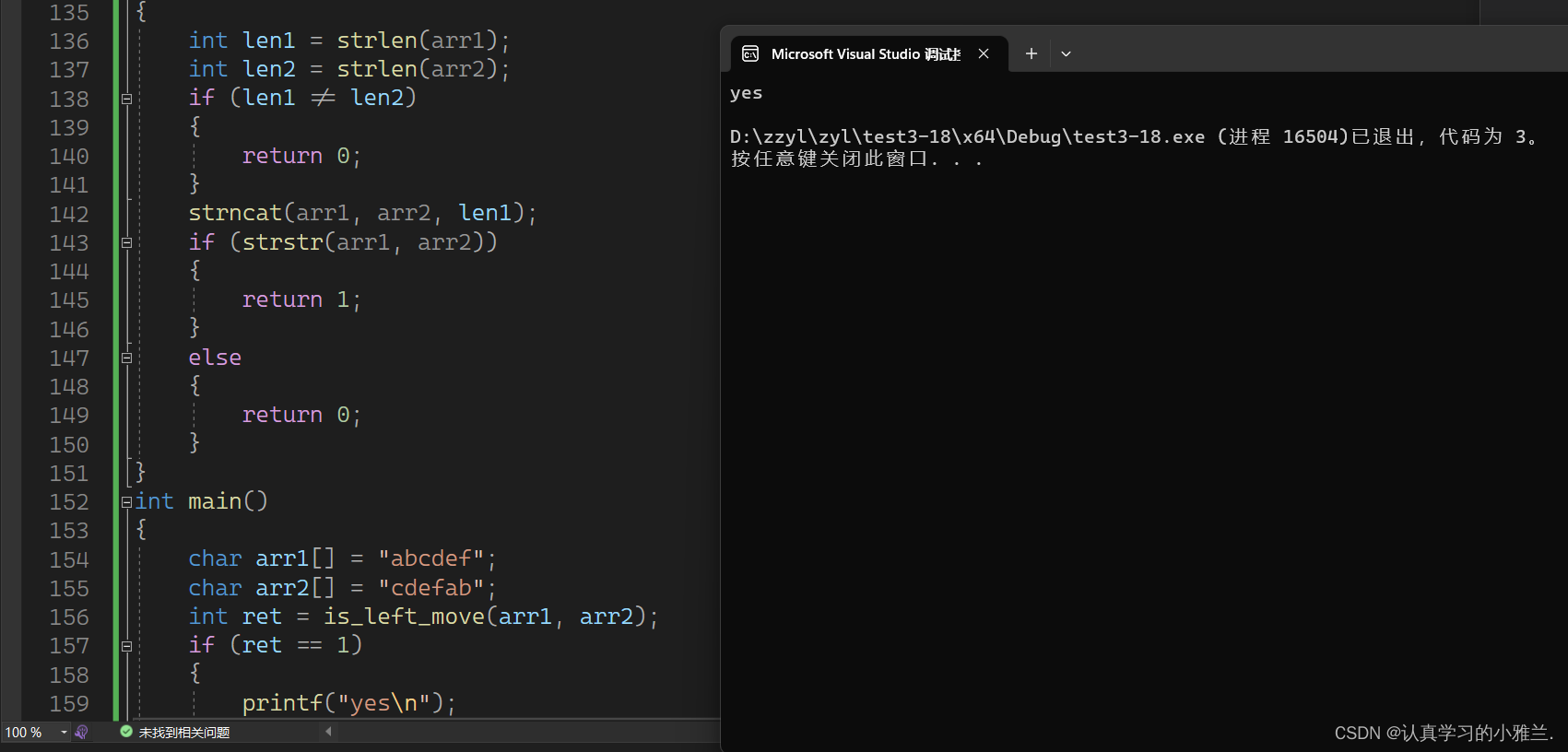
#include<stdio.h>
#include<string.h>
int is_left_move(char arr1[], char arr2[])
{int len1 = strlen(arr1);int len2 = strlen(arr2);if (len1 != len2){return 0;}strncat(arr1, arr2, len1);if (strstr(arr1, arr2)){return 1;}else{return 0;}
}
int main()
{char arr1[] = "abcdef";char arr2[] = "cdefab";int ret = is_left_move(arr1, arr2);if (ret == 1){printf("yes\n");}else{printf("no\n");}return 0;
}这个代码中运行了很多字符串函数,正好小雅兰之前写过这样的知识点:
字符函数和字符串函数(上)——“C”_认真学习的小雅兰.的博客-CSDN博客
字符函数和字符串函数(下)——“C”_认真学习的小雅兰.的博客-CSDN博客
好啦,小雅兰今天的内容就到这里啦,继续加油!!!

相关文章:

C语言刷题(7)(字符串旋转问题)——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容依旧是复习之前的知识点,那么,就是做一道小小的题目啦,下面,让我们进入C语言的世界吧 实现一个函数,可以左旋字符串中的k个字符。 例如: A…...
有趣且重要的JS知识合集(18)浏览器实现前端录音功能
1、主题描述 兼容多个浏览器下的前端录音功能,实现六大录音功能: 1、开始录音 2、暂停录音 3、继续录音 4、结束录音 5、播放录音 6、上传录音 2、示例功能 初始状态: 开始录音: 结束录音: 录音流程 …...
面试官:聊聊你知道的跨域解决方案
跨域是开发中经常会遇到的一个场景,也是面试中经常会讨论的一个问题。掌握常见的跨域解决方案及其背后的原理,不仅可以提高我们的开发效率,还能在面试中表现的更加游刃有余。 因此今天就来和大家从前端的角度来聊聊解决跨域常见的几种方式。…...
SpringCloud五大核心组件
Consul 等,提供了搭建分布式系统及微服务常用的工具,如配置管理、服务发现、断路器、智能路由、微代理、控制总线、一次性token、全局锁、选主、分布式会话和集群状态等,满足了构建微服务所需的所有解决方案。 服务发现——Netflix Eureka …...
)
Verilog HDL语言入门(二)
强烈建议用同步设计2.在设计时总是记住时序问题3.在一个设计开始就要考虑到地电平或高电平复位、同步或异步复位、上升沿或下降沿触发等问题,在所有模块中都要遵守它4.在不同的情况下用if和case,最好少用if的多层嵌套(1层或2层比较合适&#…...
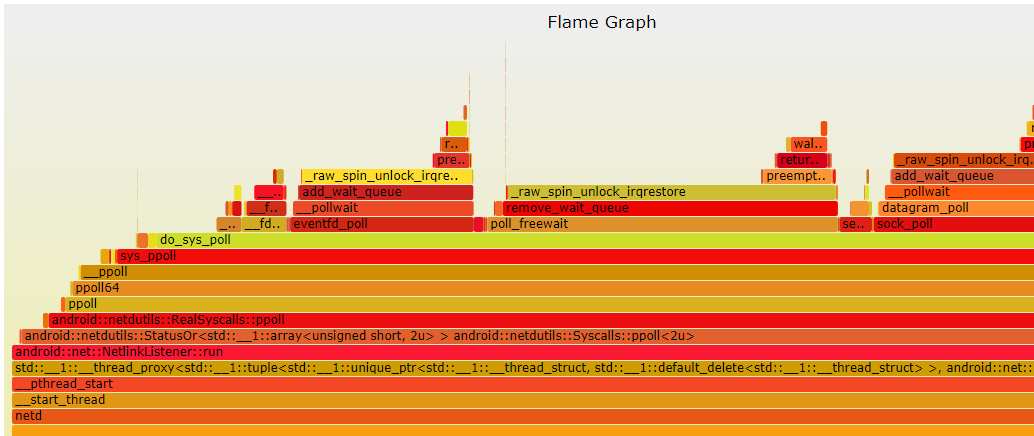
Simpleperf详细使用
一、Simpleperf介绍 Simpleperf是一个强大的命令行工具,它包含在NDK中,可以帮助我们分析应用的CPU性能。Simpleperf可以帮助我们找到应用的热点,而热点往往与性能问题相关,这样我们就可以分析修复热点源。 如果您更喜欢使用命令…...

【算法基础】二分图(染色法 匈牙利算法)
一、二分图 1. 染色法 一个图是二分图,当且仅当,图中不含奇数环。在判别一个图是否为二分图⑩,其实相当于染色问题,每条边的两个点必须是不同的颜色,一共有两种颜色,如果染色过程中出现矛盾,则说明不是二分图。 for i = 1 to n:if i 未染色DFS(i, 1); //将i号点染色未…...

Caputo 分数阶微分方程-慢扩散方程初边值问题基于L1 逼近的空间二阶方法及其Matlab程序实现
2.3.3 Caputo 分数阶一维问题基于 L1 逼近的空间二阶方法 考虑如下时间分数阶慢扩散方程初边值问题 { 0 C D t α u ( x , t ) = u...
 GPIO驱动)
I.MX6ULL_Linux_驱动篇(29) GPIO驱动
Linux 下的任何外设驱动,最终都是要配置相应的硬件寄存器。所以本篇的 LED 灯驱动最终也是对 I.MX6ULL 的 IO 口进行配置,与裸机实验不同的是,在 Linux 下编写驱动要符合 Linux 的驱动框架。I.MX6U-ALPHA 开发板上的 LED 连接到 I.MX6ULL 的 …...

jupyter的安装和使用
目录 ❤ Jupyter Notebook是什么? notebook jupyter 简介 notebook jupyter 组成 网页应用 文档 主要特点 ❤ jupyter notebook的安装 notebook jupyter 安装有两种途径 1.通过Anaconda进行安装 2.通过pip进行安装 启动jupyter notebook ❤ jupyter …...

Springboot新手开发 Cloud篇
前言: 👏作者简介:我是笑霸final,一名热爱技术的在校学生。 📝个人主页:个人主页1 || 笑霸final的主页2 📕系列专栏:后端专栏 📧如果文章知识点有错误的地方,…...

Linux:函数指针做函数参数
#include <stdio.h> #include <stdlib.h> //创建带有函数指针做参数的函数框架api //调用者要先实现回调函数 //调用者再去调用函数框架 //所谓的回调是指 调用者去调用一个带有函数指针做参数的函数框架,函数框架反过来要调用调用者提供的回调函数 …...
Vue3(递归组件) + 原生Table 实现树结构复杂表格
一、递归组件 什么是递归,Javascript中经常能接触到递归函数。也就是函数自己调用自己。那对于组件来说也是一样的逻辑。平时工作中见得最多应该就是菜单组件,大部分系统里面的都是递归组件。文章中我做了按需引入的配置,所以看不到我引用组…...
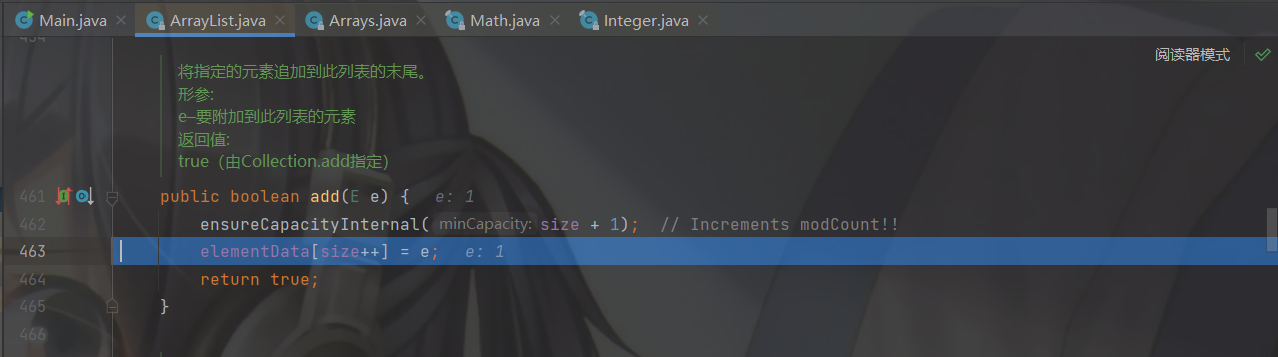
ArrayList底层源码解析
Java源码系列:下方连接 http://t.csdn.cn/Nwzed 文章目录前言一、**ArrayList底层结构和源码分析**无参构造调用创建ArrayList集合无参构造总结:发文3个工作日后 up 会把总结放入前言部分,但也诚邀读者总结,可放入评论区有参构造…...
python:DIY字符画的程序使用说明.doc
目录开发环境要求运行方法具体的操作步骤如下:代码示例源码及运行程序下载地址开发环境要求 本系统的软件开发及运行环境具体如下。 操作系统:Windows 7、Windows 10。 Python版本:Python 3.7.0。 开发工具:Python IDLE。 …...

【Python/Opencv】图像权重加法函数:cv2.addWeighted()详解
【Python/Opencv】图像权重加法函数:cv2.addWeighted()详解 文章目录【Python/Opencv】图像权重加法函数:cv2.addWeighted()详解1. 介绍2. API3. 代码示例与效果3.1 代码3.2 效果4. 参考1. 介绍 在OpenCV图像加法cv2.add函数详解详细介绍了图像的加法运…...

容器的老祖宗LXC和Docker的关系
一、什么是LXC? LXC(Linux Container的缩写)是一个基于Linux内核的容器虚拟化技术,它提供了一种轻量级、快速、简便的方式来创建和管理系统容器。与传统虚拟化技术不同,LXC并不会模拟硬件,而是利用Linux内…...
)
Webpack迁移Rspack速攻实战教程(前瞻版)
前言 rspack 即将开源,但社区中不乏有已经落地的 case ,比如 rspack-migration-showcase 、 modern.js 等。 基于此,本文将介绍如何迁移一个近似于 CRA( create-react-app ) 的项目到 rspack 。 在阅读本文前&#…...
一行代码“黑”掉任意网站
文章目录只需一行代码,轻轻一点就可以把任意网站变成暗黑模式。 首先我们先做一个实验,在任意网站中,打开浏览器开发者工具(F12),在 C1onsole 控制台输入如下代码并回车: document.documentElement.style.filterinve…...
51单片机入门 -驱动 8x8 LED 点阵屏
硬件型号、软件版本、以及烧录流程 操作系统:Windows 10 x84-64单片机:STC89C52RC编译器:SDCC烧录软件:stcgal 1.6开发板:普中51单片机开发板A2套件(2022) 在 VS Code 中新建项目到烧录的过程…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
