常见的文心一言的指令
文心一言,作为百度研发的预训练语言模型“ERNIE 3.0”的一项功能,能够与人对话互动,回答问题,协助创作,高效便捷地帮助人们获取信息、知识和灵感。以下是一些常见的文心一言指令类型及其具体示例:
1. 查询类指令
- 知识问答:用于获取特定领域的知识或定义。例如,“文心一言,请问什么是深度学习?”这类指令帮助用户快速了解某个概念或知识点。
- 天气查询:查询实时或未来的天气信息。如,“今天北京的天气怎么样?”或“请告诉我明天上海的天气预报。”
2. 生成类指令
- 文本创作:生成各种类型的文本内容,如诗歌、散文、小说、演讲稿等。例如,“文心一言,帮我写一篇关于春天的诗歌。”或“请生成一篇关于环保主题的演讲稿。”
- 图片生成:根据用户描述生成具有特定场景和元素的图片。如,“帮我生成一个玻璃瓶里面有一座城市的夜景图片,要求有魔法的水珠和电影光效。”
3. 推理类指令
- 逻辑推理:根据给定的条件进行逻辑推理,推导出结论。例如,“如果所有的猫都喜欢吃鱼,小明家养了一只猫,那么小明家的猫喜欢吃鱼吗?”
- 数学运算:执行基本的数学运算,返回计算结果。如,“5加3等于多少?”或“解方程x+2=5。”
4. 调整与优化类指令
- 调整语气和语调:用于调整文本的语气和语调,以符合特定的写作风格或读者需求。如,“文章的语气和语调可能需要调整,以更好地适应目标读者和传达所需的情感。”
- 增加论据和支持:增强文本的论点和论据的可靠性。如,“文章需要更多的论据和支持来加强观点的可信度,请添加相关的事实、数据或引用来支持观点。”
5. 特定主题类指令
- 情感分析:识别并分析文本所表达的情感倾向。如,“分析这句话‘我很高兴今天阳光明媚’的情感倾向。”
- 翻译:将一种语言的文本翻译成另一种语言。如,“将‘Hello, world!’翻译成中文。”
6. 其他类指令
- 慰藉类:提供慰藉或鼓励的话语。如,“给我一句慰藉的文心一言。”
- 励志类:提供励志的话语或名言。如,“给我一句励志的文心一言。”
这些指令类型覆盖了文心一言在信息查询、文本创作、逻辑推理、情感分析、翻译等多个方面的功能,体现了其自然语言处理能力的广泛性和实用性。用户可以根据自己的需求,构造复杂或特定的指令,文心一言将尽力理解和执行。
相关文章:

常见的文心一言的指令
文心一言,作为百度研发的预训练语言模型“ERNIE 3.0”的一项功能,能够与人对话互动,回答问题,协助创作,高效便捷地帮助人们获取信息、知识和灵感。以下是一些常见的文心一言指令类型及其具体示例: 1. 查询…...
)
数字货币交易接口实现(含源代码)
数字货币交易接口实现(含源代码) 使用币安交易接口步骤1:注册API密钥步骤2:安装所需库步骤3:使用API进行交易获取市场数据查看账户信息执行交易错误处理安全提示 使用OKX交易接口步骤1:注册API密钥步骤2&am…...

c++函数以及函数分文件编写
1.函数 1.1格式 返回值类型 函数名 (参数列表)//返回值类型指的是return过去的类型 { 函数体语句 return 表达式 } 1.2常见的函数样式 1.无参返回 2.有参返回 3.无参有返 4.有参有返 #include<iostream> using namespace std; int add(int nu…...

【JVM基础06】——组成-直接内存详解
目录 1- 引言:直接内存概述1-1 直接内存是什么?直接内存的定义(What)1-2 为什么用直接内存?Java程序对直接内存的使用 (Why) 2- ⭐核心:详解直接内存(How)2-1 文件拷贝案例介绍对比常规 IO(BIO) 和 NIO常规 IO 的操作流程NIO 的操…...

学术研讨 | 区块链与隐私计算领域专用硬件研讨会顺利召开
学术研讨 近日,国家区块链技术创新中心主办,长安链开源社区支持的“区块链与隐私计算领域专用硬件研讨会”顺利召开,会议围绕基于区块链与隐私计算的生成式AI上链、硬件加速、软硬协同等主题展开讨论,来自复旦大学、清华大学、北京…...

AngularJS API 深入解析
AngularJS API 深入解析 AngularJS,作为一个强大且灵活的JavaScript框架,自从其诞生以来,就一直是前端开发者构建复杂Web应用的首选工具。本文将深入探讨AngularJS的API,帮助读者理解其核心功能和工作原理。 AngularJS简介 AngularJS由Google开发,并于2010年发布。它是…...

过某开源滑动验证码
过某开源滑动验证码 今天早上我有一点空闲时间,想着回顾一下前几天在某查询网站遇到的滑动验证码,以免时间久了忘记了。那个网站可能使用的是较早版本的开源滑块验证码系统tianai-captcha,但我不确定是否正确。 整体思路: 获取…...

一文解决 | Linux(Ubuntn)系统安装 | 硬盘挂载 | 用户创建 | 生信分析配置
原文链接:一文解决 | Linux(Ubuntn)系统安装 | 硬盘挂载 | 用户创建 | 生信分析配置 本期教程 获得本期教程文本文档,在后台回复:20240724。请大家看清楚回复关键词,每天都有很多人回复错误关键词…...

Matlab M_map工具箱绘制Interrupted Mollweide Projection
GMT自带了许多的地图投影,但是对于Interrupted Mollweide投影效果却不好。 作为平替的m_map工具箱中带有的投影类型可完美解决这一问题。 Interrupted Mollweide Projection长这样 全球陆地 全球海洋 使用Matlab工具箱m_map展示全球海平面变化的空间分布 addpath(…...

Python 变量与基本数据类型
重点内容 1 掌握变量及厂里在数据输入、输出及计算中的应用; 2 熟练使用datetime模块来处理日期和时间问题; 3 熟练掌握abs()、round()、pow()、sum()、min()、max()等的应用; 4 利用变量、字符等知识模拟开发中一些场景的输入与输出&…...

Pytorch深度学习实践(5)逻辑回归
逻辑回归 逻辑回归主要是解决分类问题 回归任务:结果是一个连续的实数分类任务:结果是一个离散的值 分类任务不能直接使用回归去预测,比如在手写识别中(识别手写 0 − − 9 0 -- 9 0−−9),因为各个类别…...

认识漏洞-GitLab 远程命令执行漏洞、致远OA-ajax.do未授权任意文件上传漏洞
为方便您的阅读,可点击下方蓝色字体,进行跳转↓↓↓ 01 [GitLab 远程命令执行漏洞复现(CVE-2021-22205)](https://mp.weixin.qq.com/s/4QT-vxKpBn4ppNM9ipt-nQ)02 [致远OA-ajax.do未授权任意文件上传Getshell](https://mp.weixin.qq.com/s/TH2A5J5TXU36Y…...

vue实现电子签名、图片合成、及预览功能
业务功能:电子签名、图片合成、及预览功能 业务背景:需求说想要实现一个电子签名,然后需要提供一个预览的功能,可以查看签完名之后的完整效果。 需求探讨:后端大佬跟我说,文档我返回给你一个PDF的oss链接…...

【flink】之如何消费kafka数据?
为了编写一个使用Apache Flink来读取Apache Kafka消息的示例,我们需要确保我们的环境已经安装了Flink和Kafka,并且它们都能正常运行。此外,我们还需要在项目中引入相应的依赖库。以下是一个详细的步骤指南,包括依赖添加、代码编写…...

科研绘图系列:R语言山脊图(Ridgeline Chart)
介绍 山脊图(Ridge Chart)是一种用于展示数据分布和比较不同类别或组之间差异的数据可视化技术。它通常用于展示多个维度或变量之间的关系,以及它们在不同组中的分布情况。山脊图的特点: 多变量展示:山脊图可以同时展示多个变量的分布情况,允许用户比较不同变量之间的关…...

Boost搜索引擎:如何建立 用户搜索内容 与 网页文件内容 之间的关系
如果想使“用户搜索内容”和“网页文件内容”之间产生联系,就应该将“用户搜索内容”和“网页文件”分为很小的单元 (这个单元就是关键词),寻找用户搜索单元是否出现在这个文档之中,如果出现就证明这个网页文件和用户搜…...
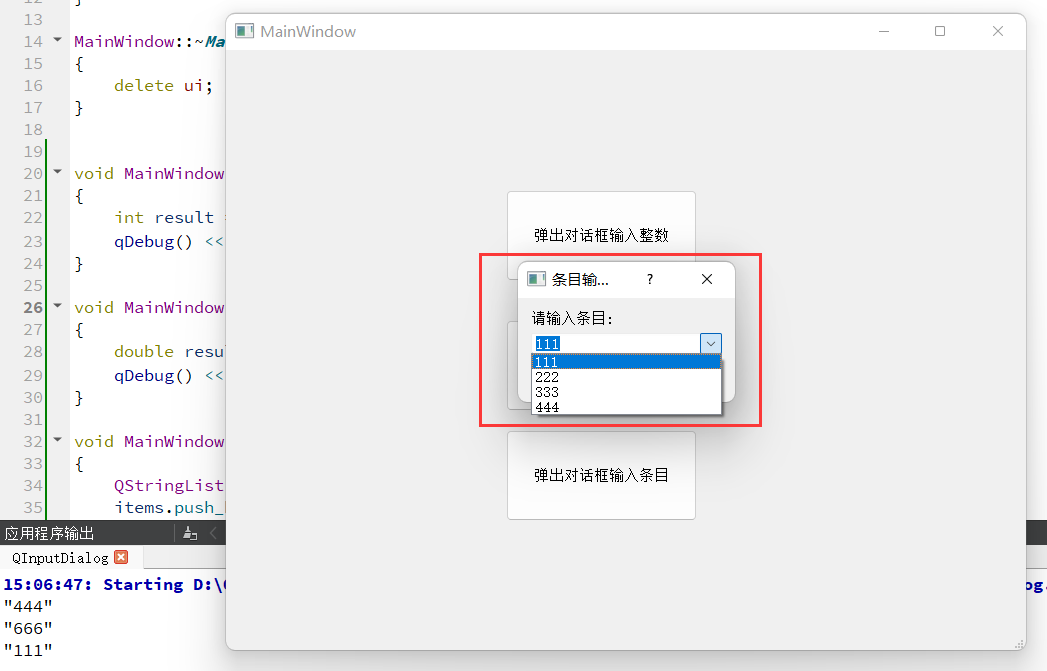
【QT】QT 窗口(菜单栏、工具栏、状态栏、浮动窗口、对话框)
Qt 窗口是通过 QMainWindow类来实现的。 QMainWindow 是一个为用户提供主窗口程序的类,继承自 QWidget 类,并且提供了⼀个预定义的布局。QMainWindow 包含一个菜单栏(Menu Bar)、多个工具栏(Tool Bars)、…...

Golang | Leetcode Golang题解之第283题移动零
题目: 题解: func moveZeroes(nums []int) {left, right, n : 0, 0, len(nums)for right < n {if nums[right] ! 0 {nums[left], nums[right] nums[right], nums[left]left}right} }...
ubuntu22.04 安装 NVIDIA 驱动以及CUDA
目录 1、事前问题解决 2、安装 nvidia 驱动 3、卸载 nvidia 驱动方法 4、安装 CUDA 5、安装 Anaconda 6、安装 PyTorch 1、事前问题解决 在安装完ubuntu之后,如果进入ubuntu出现黑屏情况,一般就是nvidia驱动与linux自带的不兼容,可以通…...
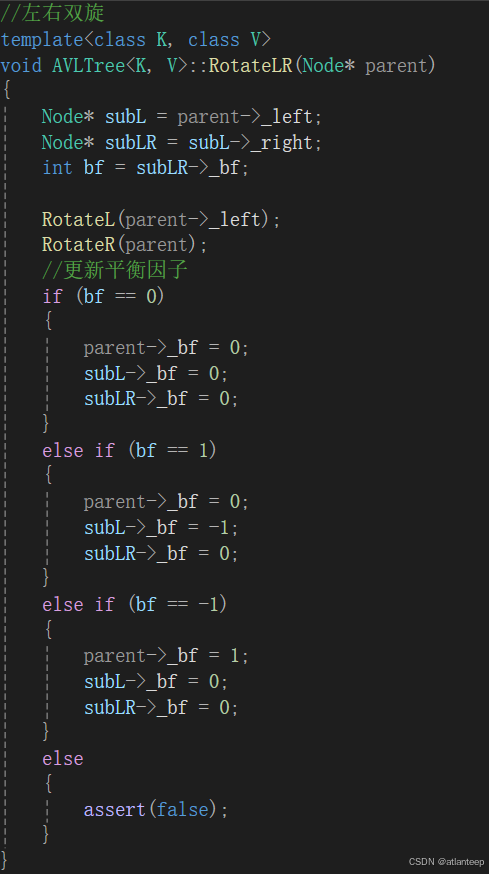
数据结构·AVL树
1. AVL树的概念 二叉搜索树虽可以缩短查找的效率,但如果存数据时接近有序,二叉搜索将退化为单支树,此时查找元素效率相当于在顺序表中查找,效率低下。因此两位俄罗斯数学家 G.M.Adelson-Velskii 和E.M.Landis 在1962年发明了一种解…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
