理想发周榜,不是新能源市场的原罪
余华在他的小说《在细雨中呼喊》曾写过这么一段话:
“仓廪实而知礼节,衣食足而知荣辱”,在物质需求得到满足以前,精神文明的发展难免会有所滞后。所以,贫穷,不是原罪。
同样的,在如今的新能源市场,车企们的生存环境也异常严峻。行业的集中度由2022年的59.9%上升至2023年的67.0%,并且据艾睿铂咨询预计,中国的新能源车品牌的数量可能从2023年的137个急剧减少到2030年的19个。
在这种环境里,价格战、价值战、舆论战等手段的目的只有一个:让企业更好地活下去。因此,很多车企都将销量榜排名作为舆论制高点,以此来宣传自己。
正是在这样的背景下,7月30日,理想汽车照常发布了最近一周的销量榜单。只不过,和以往不同的是,这次的周榜却引发了蔚来、小鹏、吉利等品牌的高管们的集体反对,颇有几分“六大派围攻光明顶”的意思。
从以前的“年榜”“月榜”再到如今的“周榜”,榜单的累计时间为何越来越短?新能源行业越来越“卷”的根本原因是什么?激烈的竞争之后,中国新能源车的未来会是怎样的?
理想被怼的背后,每一家车企都有“最适合自己”的那个榜
从各家高管公开发表的观点来看,不同的品牌的侧重点有所不同。
蔚来品牌与传播助理副总裁马麟认为,周榜的数据已经影响到了企业的经营,同时榜单把主营产品价位不同、品类不同的车企放在了一起,这并不能反映市场的客观情况。“做榜单,一定要合理,彼此之间要可比。”并且这并不是蔚来方面首次反对周榜,此前蔚来董事长李斌就曾在NIO IN 2024蔚来创新科技日活动上表示:“能不能不发周榜?如果蔚来做到(销量)第一,永远不发周榜。”
与此同时,小鹏和吉利则是把关注点放在了整个行业。小鹏汽车董事长何小鹏认为:“美国人在想怎么把端到端自动驾驶辅助技术做得更好,怎么能够做得比人更好,比如特斯拉,端到端大模型之后,FSD和之前完全不一样,明年美国智驾端到端系统产品就要比老司机更强。中国的科技公司还在干‘周销量榜’,这不是科技竞争该有的样子。”随后,吉利控股高级副总裁杨学良对何小鹏的看法表示了赞同,“我也反对出周榜。”
然而,早在2023年4月,理想就已经开始主动公布周销量榜,并且采用的是第三方机构数据。虽然与乘联会每月公布的销量数据的统计口径不同,但数据来源真实有效,经得起实践的检验。这也就是为什么理想汽车董事长李想在受到外界的质疑之后,拥有敢于在朋友圈回应的底气。

此前,MEGA销量遇冷时,理想也曾暂停过周榜数据的更新,李想在当时表示:“不再追求销量,而是回到价值。”而从行业来看,销量榜单也不只是理想汽车一家的行为,很多汽车厂商和汽车媒体,都通过大量的定语做前缀,做出了大量的细分市场的榜单。

“只要定语加得够多,总能排到第一”,这些榜单和理想的周榜的目的是一致的:让自家的品牌或车型处于榜单头部位置,利用销量榜单制造舆论话题,吸引消费者的关注,从而提升品牌形象、促进销量的增长。
从早初每家车企进行正常的季度数据披露,再到后来的乘联会月度销量榜,再到如今的周榜,榜单频率的提升对消费者来说其实意义不大,毕竟没有人会单纯地因为销量高就选择某款车。反倒是整个行业的营销手段在加码,舆论战在不断升级,行业的“内卷”在不断地加剧,传递到每个企业头上的压力太大,因此才会产生对榜单的争议。
从这个角度来看,榜单有争议,并不是理想一家的错,而是整个行业的错。
怎么“卷”,才是高效的“卷”?
当下,关于“卷”的感叹和讨论,人们已经听得太多了。因此,不妨从另一个角度来看待这个问题,或许会有不同的收获。

从经济学角度来讲,“卷”意味着“完全竞争”,而在“完全竞争”的市场里,企业最多也只能做到“收支平衡”,无法赚取“超额利润”,因为只要有企业能赚到钱,马上就有其他企业进入,把利润“卷”光。
现实里,一个“完全竞争”的市场是罕见的。以中国为例,手机支付由微信和支付宝垄断。电商、外卖也都是由几大平台主导。尽管竞争格局会有变化,但整体态势仍然相对稳定。除非像字节跳动和拼多多这类企业,对行业提出了颠覆式创新,才能实现弯道超车,否则很难有新的企业加入进来。
不过,从2023年开始,整个行业陷入了价格战的泥潭。上半年,燃油车大面积降价;下半年,比亚迪、蔚来、零跑等新能源品牌也都在不同程度上发起了价格攻势。这种价格战虽然在一定程度上促进了销量的增长,但也牺牲了企业的利润,导致毛利率下滑,部分车企甚至面临亏损的困境,导致如今的新能源车市场就非常接近这种“完全竞争”的状态。
而之所以会出现这样的状态,主要原因有两点:
1.产品同质化,不同品牌的产品之间,并不存在决定的不可复制或不可替代性,因此不存在绝对的品牌溢价,没有“杀手”级别的产品出现。
2.没有任何一个卖家有绝对的成本优势,即使是比亚迪、特斯拉等企业能够依靠相对完整的产业链取得了暂时的成本优势。如今,在其他厂商的追赶下,这种优势也在逐渐减小,整个行业的规模效应、网络效应等尚未形成。

因此,想要破局,光靠销量排名榜单显然是远远不够的,必须从产品本身入手:要么利用产品的“先发优势”及“红利”,帮助企业在产品周期内放量销售,建立阶段性的利润优势;要么凭借更大规模的销售量,从而掌握更强的向下定价能力,建立阶段性的成本优势;要么凭借产品在红利周期内获取的资源(数据积累、技术积累),建立阶段性的技术优势;
从这个角度来看,不断地推陈出新,推出能够在短期内形成有“先发优势”的差异化产品,捕捉新的产品红利,让竞争对手承受巨大的竞争压力,始终无法有效追赶,一直蒙受巨大损失,最终被迫退出。这才是企业想要脱颖而出的正解。
“内卷”的尽头,是“外卷”
事实上,“内卷”不仅仅是新能源行业独有的问题。过去的共享单车、网约车、外卖等行业也都曾出现类似的场景。在这些行业发展的早期,也是多方势力互相角力,最终都是通过“烧钱”来决定阶段性竞争成败,最终剩下几家巨头存活到最后。
而且不仅仅是中国,放眼全球市场,同样的案例比比皆是。只要有人的地方,就有江湖;只要有利润的地方,就必然存在竞争。工业革命以后形成的行业以及外来输入行业,多半是寡头垄断行业。汽车、家电、手机、电脑、饮料、方便食品工业革命产生的行业,都是少数几家(通常是3家-5家)居于垄断地位。外部输入行业,如啤酒、乳制品等,同样是高度集中。
具体到汽车行业,在燃油车时代,全球市场在经历了两次世界大战之后,又经过了几十年的竞争,才形成了后来欧美日三国车企寡头垄断的局面。市场上现存的国际品牌,都是大浪淘沙后留下来的幸运儿,是走出企业生存周期“大筛子”的成功者。
只不过,相比之下,中国新能源市场这一轮的竞争更加激烈,节奏和速度更快而已。从最终结果来看,过去的“卷”和现在的“卷”不会相差太多,最终也会“卷”到只剩几个巨头竞争的局面。虽然最终的结果谁胜谁负难以预测,最终企业的个数也不可知,需要多长的时间也不可知,但是可以肯定的一点是,在这样残酷的竞争中成长起来的中国企业,一定拥有更强的国际竞争力。
毕竟,大家在讨论国内的新能源车品牌的卷的同时,大众、BBA等传统车企在中国市场的份额都已经有所下滑,悄悄地让出了舞台中心的位置。不仅如此,在广大的欧美市场和亚非拉市场,中国的新能源车企也展现出了极强的竞争力,“卷”出国门,对当地市场的本土品牌发起了进攻。
从这个角度来看,在这一轮的寡头之间的“换届”中,全球的汽车市场必然会经历一轮“东升西落”的迭代。毕竟,中国车企在国内卷不赢还可以出海,外国车企在中国市场卷不赢就真的只能卷铺盖了。
来源:港股研究社
相关文章:

理想发周榜,不是新能源市场的原罪
余华在他的小说《在细雨中呼喊》曾写过这么一段话: “仓廪实而知礼节,衣食足而知荣辱”,在物质需求得到满足以前,精神文明的发展难免会有所滞后。所以,贫穷,不是原罪。 同样的,在如今的新能源…...

AHK是让任何软件都支持 Shift + 鼠标滚轮 实现界面水平滚动
目录 基本介绍 详细特点 图解安装 下载失败?缓慢? 创建并运行脚本代码😃 新建空 xxx.ahk文件 vscode/记事本等编辑工具打开 复制并粘贴简易脚本 运行 其他问题 问题一:弹出无法执行此脚本 关闭脚本 基本介绍 AutoHot…...

如何在C语言中实现求解超级丑数
超级丑数是一个正整数,并且它的质因数只包含在给定的质数列表中。超级丑数的定义类似于丑数,但可以根据特定需求改变质因数的范围。下面是如何在C语言中实现求解超级丑数的代码。 我们使用最小堆(优先队列)来高效地生成超级丑数序…...

secExample靶场之java反序列化漏洞复现
我是使用kali虚拟机搭建的靶场,具体搭建步骤可以看我之前的博客内容。 访问靶机地址,打开java反序列化的 点进去后是如图的页面,随便输入一信息。 可以看到敏感信息直接显示在了页面上。 访问192.168.189.141:8080/cors1,可以看到…...

解决升级Linux内核后,open files设置无效的问题。
问题过程 操作系统是OpenEuler 20.03,内核由4.19.90-2112.8.0.0131.oe1.aarch64升级到kernel-4.19.90-2401.1.0.0233.oe1.aarch64后,重启系统后,重新开起来运行OceanBase就运行不起来了,提示open files must not be less than 20…...

关于防范勒索病毒Play新变种的风险提示
近日,工业信息化部网络安全威胁和漏洞信息共享平台监测发现针对 Linux的勒索病毒Play新变种,攻击对象主要为VMware ESXi 虚拟化环境,攻击目标包括制造、建筑业、IT、金融和房地产等行业。 Play勒索病毒又名 Balloonfly和PlayCrypt࿰…...
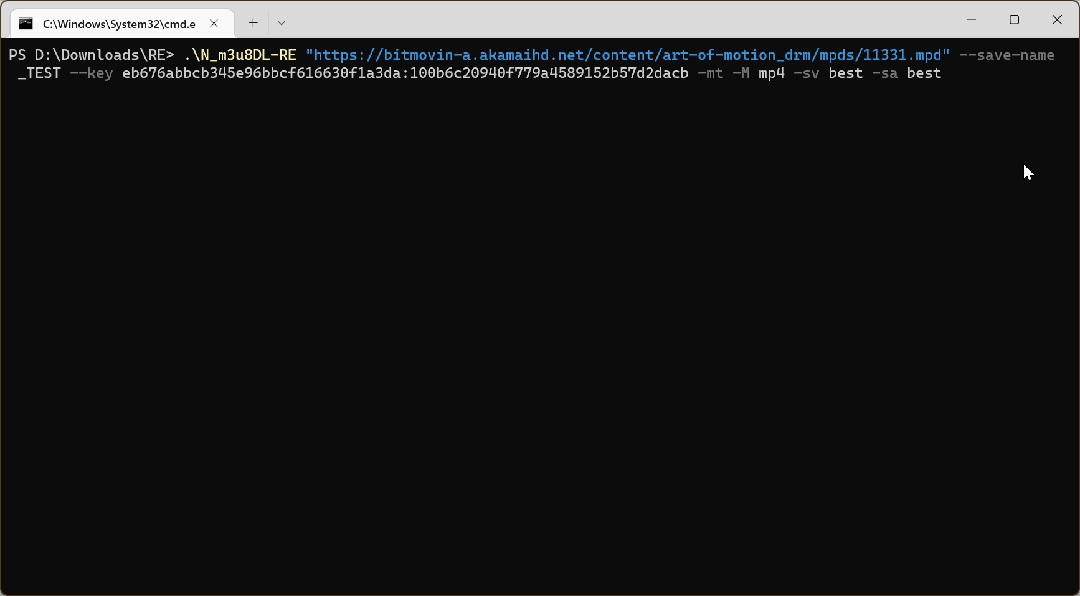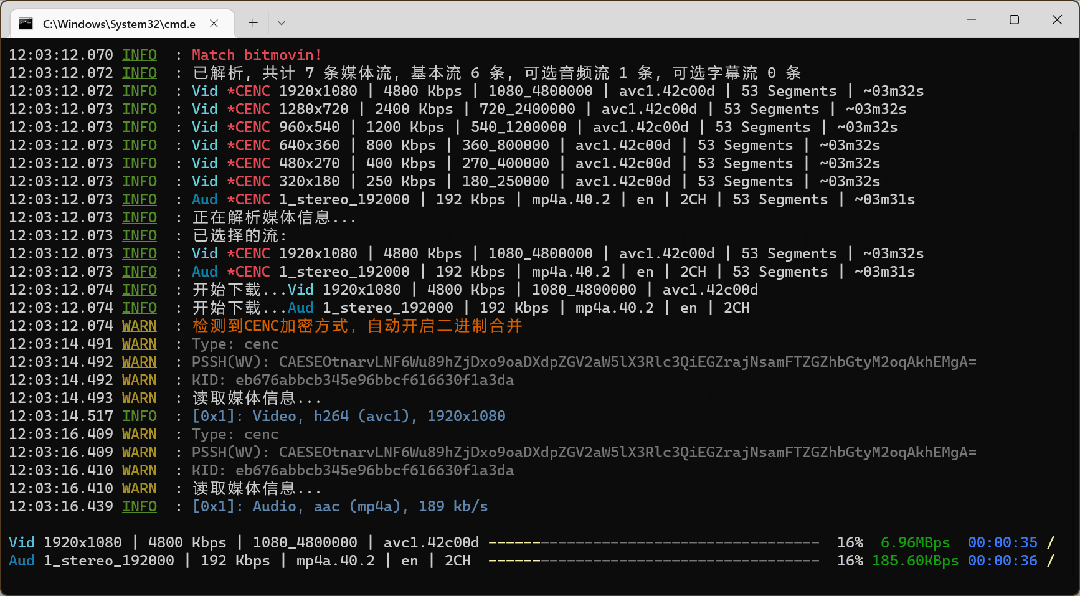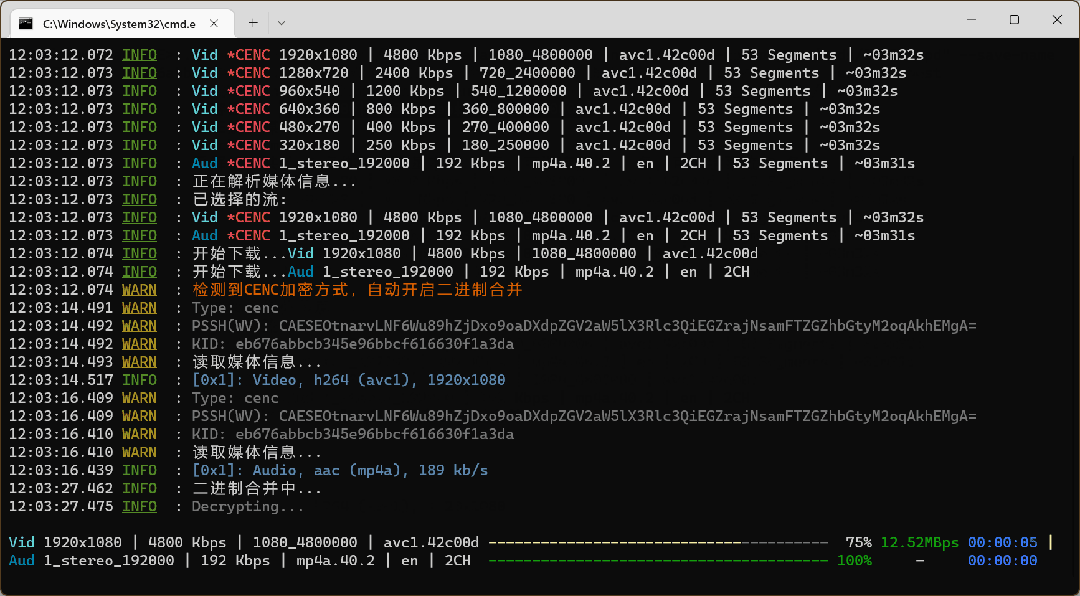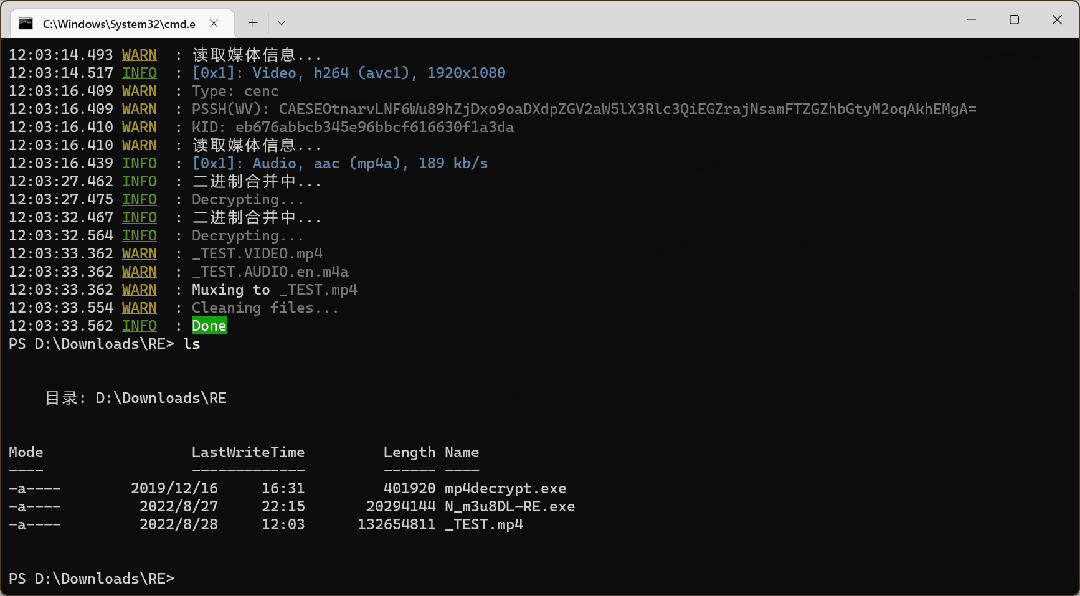
一款.NET开源、跨平台的DASH/HLS/MSS下载工具
前言 今天大姚给大家分享一款.NET开源(MIT License)、免费、跨平台的DASH/HLS/MSS下载工具,并且支持点播和直播(DASH/HLS)的内容下载:N_m3u8DL-RE。 网络流媒体传输协议介绍 DASH DASH是一种基于HTTP的…...

MATLAB学习日志DAY21
结构体(2) 如果将生成逗号分隔列表的表达式括在方括号中,MATLAB 会将该列表中的每一项都存储在数组中。示例中,MATLAB 创建一个数值行向量,该向量包含结构体数组 S 的每个元素的 score 字段: scores [S.…...

Spingboot请求tcp 方式
import lombok.extern.slf4j.Slf4j; import org.springframework.stereotype.Service;import java.io.IOException; import java.net.InetSocketAddress; import java.nio.ByteBuffer; import java.nio.channels.SocketChannel;/*** 请求tcp接口** author Mr丶s* date 2024/7/1…...

leetcode刷题日记-括号生成
题目描述 题目解析 回溯的题目,不过这个两个if我就感觉有点难以理解了,不过仔细的思考了一下,确实考虑到了每个位置的情况,特别是针对右边括号 题目代码 class Solution:def generateParenthesis(self, n: int) -> List[str…...

小程序按钮分享
使用button设置: open-type"share":来微信分享; html: <button open-type"share"></button>...

多模态多智能体,在实现系统2(深思熟虑)方面的探索
多模态和多智能体,在系统2(深思熟虑)方面的探索 提出背景理性的定义为什么理性定义是四大基本原则,而不是其他数量,又为何是这四个,而不是其他?理性 不等于 推理 通过多模态多智能体系统增强理性…...
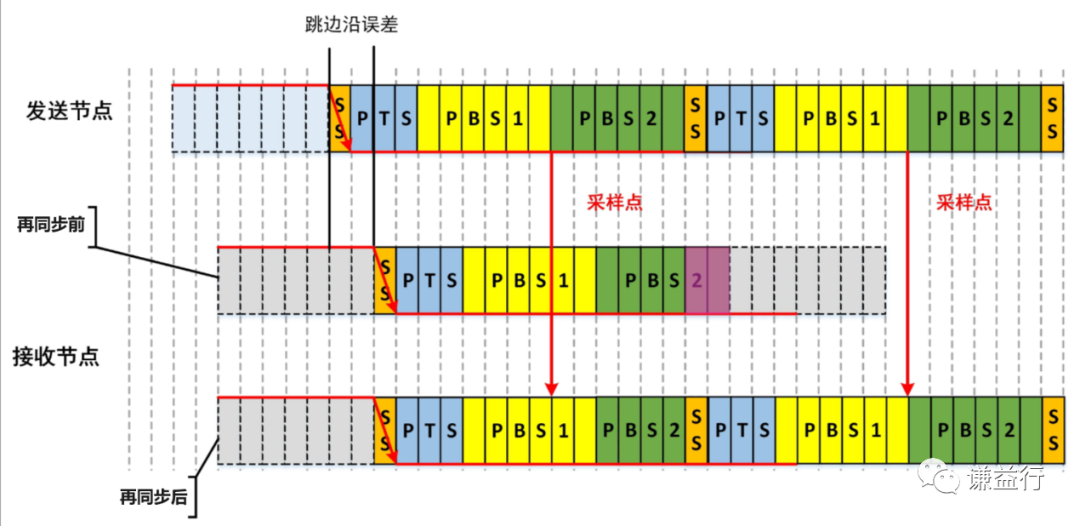
【CAN通讯系列8】如何准确接收数据?
在 【CAN通讯系列7】波特率是什么?已经介绍了CAN位时间和采样点等概念,每1位由同步段(SS)、传播时间段(PTS)、相位缓冲段1(PBS1)和相位缓冲段2(PBS2)四个段组成,这个也成为位时序,采样点位置处于PBS1和PBS2的交界处,如…...

RabbitMQ知识总结(基本概念)
文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 基本概念 Producer: 消息的生产者,是一个向…...

Prel语言入门学习:一篇全面的指南
引言 在编程语言的海洋中,Prel是一个较少人知的新星。作为一种专为数据处理和分析设计的语言,Prel结合了现代编程语言的简洁性与功能性,提供了一种独特的解决方案,尤其适用于数据科学家和分析师。本文将详细介绍Prel语言的基础&am…...

在云服务器上自动化部署项目,jenkins和gitee
▮全文概述 在编写项目时,很头大的事情就是需要自己手动的上传jar包到服务器上启动。如果出现一点bug,就要重头上传和启动。这是一件很烦的事情,所以,可以使用jenkins和gitee实现项目的自动部署 ▮全流程 在本地提交代码到gitee …...

python 参数输入
在 Python 中,参数输入通常有多种方式,这取决于你要从何处获取参数。以下是几种常见的方法: 1. 命令行参数 使用 sys.argv 获取命令行参数,或者使用 argparse 模块进行更复杂的参数解析。 示例 1: 使用 sys.argv import sys# …...

Spring面试篇章——Spring基本概述
Spring 的基本概述 Spring学习的核心内容—一图胜千言 IOC:控制反转,可以管理 Java 对象AOP:切面编程JDBCTemplate:是Spring提供一套访问数据库的技术,应用性强,相对好理解声明式事务:基于IOC …...

股票预测模型中注意力多层Attention RNN LSTM 的应用
全文链接:https://tecdat.cn/?p37152 原文出处:拓端数据部落公众号 Attention 机制是一种在神经网络处理序列数据时极为关键的技术,它赋予了模型“聚焦”能力,能够自动评估输入序列中各部分的重要性。通过为序列中的每个元素分…...

C语言 | Leetcode C语言题解之第313题超级丑数
题目: 题解: int nthSuperUglyNumber(int n, int* primes, int primesSize) {long dp[n 1];int pointers[primesSize];for (int i 0; i < primesSize; i) {pointers[i] 0;}long nums[primesSize];for (int i 0; i < primesSize; i) {nums[i] …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
