Python数值计算(12)——线性插值
1. 概述
插值是根据已知的数据序列(可以理解为你坐标中一系列离散的点),找到其中的规律,然后根据找到的这个规律,来对其中尚未有数据记录的点进行数值估计的方法。最简单直观的一种插值方式是线性插值,它是数学、计算机图形学等领域广泛使用的一种简单插值方法,根据已知数据点来估某一点的函数值。线性插值法的特点是简单、方便,适用于函数在某一段区间内是线性的情况,即函数在该区间内可以用一条直线来近似表示。线性插值法的优点是计算量小,缺点是对于。多个点而言在连接点出出在明显的间断点。
2. 一点数学知识
线性插值是简单直观的,假设已知坐标与
,要得到
区间内某一位置
在直线上的
值,根据点斜式直线方程
,我们只需要求出斜率
即可,显然有:
则:
如果写成斜截式:
当然如果时,就违背了函数单一性原则(不讨论广义上的曲线)。
对于多个点,可以在每个区间段内采用分段线性插值。
3. 算法实现
3.1 单段线性插值
单段线性插值就是确定一个线性函数,然后通过函数估算其他点处的函数值。
以下定义个函数,返回一个多维数组,表示多项式的系数,并通过该返回值创建多项式,随后计算处的值,并在图形中表示:
import numpy as np
from numpy.polynomial import Polynomial
import matplotlib.pyplot as pltdef linear_2p(x:np.ndarray,y:np.ndarray):k=(y[1]-y[0])/(x[1]-x[0])b=y[0]-k*x[0]return np.array([b,k])x=np.array([2,5])
y=np.array([3,7])coef= linear_2p(x,y) # 线性插值函数的系数
p=Polynomial(coef) # 构造多项式
print(p) # 0.33333333 + 1.33333333 x
print(p(2.5)) # 3.6666666666666665# 绘制图形
X=np.linspace(x[0],x[1],100)
Y=p(X)
plt.plot(X,Y,'r')
#plt.plot(x,y,’r’)
#注:这两种在线性时绘图效果相同,
# 但是实际含义不同,前者是用多个点绘制拟合曲线,
# 后者仅用线段连接起止点
plt.plot(2.5,p(2.5),'b*')
plt.grid()
plt.show()
绘制图形如下:

如果需要计算单个点或者多个点的插值,其实不需要去计算该段的直线,也可以使用定比分点的概念:
因此,插值可以使用如下函数:
def linear_2p_intp(x:np.ndarray,y:np.ndarray,w):t=(w-x[0])/(x[1]-x[0])
return (1-t)*y[0]+t*y[1]例如,实现5个点的插值并显示:
x=np.array([2,5])
y=np.array([3,7])
w=np.linspace(3,4,10)
plt.plot(x,y,'r') # 简化绘图
yw=linear_2p_intp(x,y,w)
plt.plot(w,yw,'b*')
plt.grid()
plt.show()
运行效果如下:

动态演示效果如下:

3.2 多段线性插值
多段线性插值在每一段上都是两点线性插值,假设点序列(X,Y)中X为单调递增,即具有如下特点:
估算x=w点处的值时,首先需要定位w属于哪个区间段,
为此,在构造该算法时,除了需要各段的函数外,还要有各段的区间信息,定义类如下:
from scipy.interpolate import PPoly
import numpy as np
from numpy.polynomial import Polynomial as P
import matplotlib.pyplot as pltclass multiSegLinearIntp:__coef:np.ndarray # coefficient__bps:np.ndarray # breakpoints__seg=0 # segments countdef __init__(self,x:np.ndarray,y:np.ndarray):n,=x.shapek=np.diff(y)/np.diff(x)self.__coef=np.zeros((2,n-1))self.__coef[0,:]=y[0:-1]-k*x[0:-1]self.__coef[1,:]=kself.__bps=x.copy()self.__seg=n-1def __call__(self,x:np.ndarray):n,=x.shapey=np.zeros(n)for i in range(n):w=x[i]if w<self.__bps[0]:y[i]=self.__coef[0,0]+self.__coef[1,0]*wcontinueif w>=self.__bps[-1]:y[i]=self.__coef[0,-1]+self.__coef[1,-1]*wcontinuej=0while w>=self.__bps[j]:j+=1y[i]=self.__coef[0,j-1]+self.__coef[1,j-1]*wreturn y@propertydef c(self):return self.__coef@propertydef seg(self):return self.__seg
该类multiSegLinearIntp的构造函数将numpy.ndarray的实例x和y作为参数,内部保存各分段区间的系数,实例对象在收到传入值x后,查找x其所在的分段,并在该段返回函数的值,测试如下:
x=np.array([0,1,2,3,4,5,6,7,8,9])
y=np.array([2,4,3,3,1,5,6,3,1,0])z=multiSegLinearIntp(x,y)
x1=np.linspace(-2,11,200)
y1=z(x1)
plt.plot(x,y,'r')
w=np.array([-2,11])
print(z(w)) #[-2. -2.]
#plt.plot(x1,y1,'b-')
#y2=np.interp(x1,x,y)
#plt.plot(x1,y2,'g*')
plt.grid()
plt.show()x=np.array([0,1,2,3,4,5,6,7,8,9])
y=np.array([2,4,3,3,1,5,6,3,1,0])z=multiSegLinearIntp(x,y)
x1=np.linspace(-2,11,200)
y1=z(x1)
plt.plot(x,y,'r')
w=np.array([-2,4.5,11])
yw=z(w)
print(z(w)) #[-2. 3. -2.]
plt.plot(w,yw,'b*')
plt.grid()
plt.show()
运行效果如下:

可以看到,在点处计算的值为
,这是相符的,对于不在区间内的点
和
,可以看到依旧保持了这种线性关系,这就已经是外插了(extrapolation),是否要应用这种关系,需要根据实际情况判断。
动态演示效果如下:

4. 现有工具包
通过前面一节的例子,发现自己实现的多段线性插值还是挺麻烦的,有现场的工具包吗?当然。numpy中,使用numpy. Interp函数实现插值运算,其函数原型为:
numpy.interp(x, xp, fp, left=None, right=None, period=None)其中x是待估算值的横坐标,xp,fp是已知点序列,left和right是x没有落在插值区间时的值,缺省值是left=x[0],right=x[-1],period是周期型,通常用于角坐标的插值,返回值是与x具有同样长度的多维数组。
测试如下:
x=np.array([2,5])
y=np.array([3,7])
w=np.linspace(3,4,5)
print(linear_2p_intp(x,y,w))
print(np.interp(w,x,y))
'''
输出均为[4.33333333 4.66666667 5 5.33333333 5.66666667]
'''另外,在scipy软件包中,scipy.interpolate.interp1d类也可以实现线性插值,但是该类已经作为遗留代码,不在被更新,在以后得升级中可能会被移除,官方给的建议是使用前面提到的numpy.interp函数。以下是简单的一个示例,供参考:
x=np.array([2,5])
y=np.array([3,7])
w=np.linspace(3,4,5)
f=interp1d(x,y)
plt.plot(w,f(w),'r*-')
plt.grid()
plt.show()运行效果为:

5. 双线性插值
双线性插值(Bilinear interpolation)是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。 假如我们想得到未知函数 在点
的值,假设我们已知函数 f 在
四个点的值。首先在
方向进行线性插值,然后在
方向进行线性插值。这种插值方法并不是线性的,而是两个线性函数的乘积。线性插值的结果与插值的顺序无关。首先进行
方向的插值,然后进行
方向的插值,所得到的结果是一样的。
基本数学原理如下:
先在方向插值:
然后在方向插值:
在现有工具包中,scipy.interpolate.LinearNDInterpolator可以实现该功能。
相关文章:
Python数值计算(12)——线性插值
1. 概述 插值是根据已知的数据序列(可以理解为你坐标中一系列离散的点),找到其中的规律,然后根据找到的这个规律,来对其中尚未有数据记录的点进行数值估计的方法。最简单直观的一种插值方式是线性插值,它是…...

TypeScript(switch判断)
1.switch 语法用法 switch是对某个表达式的值做出判断。然后决定程序执行哪一段代码 case语句中指定的每个值必须具有与表达式兼容的类型 语法switch(表达式){ case 值1: 执行语句块1 break; case 值2: 执行语句块3 break; dfault: //如…...

血细胞自动检测与分类系统:深度学习与UI界面的结合
一、项目概述 项目背景 在医学实验室中,血细胞的检测和分类是诊断和研究的重要环节。传统方法依赖于人工显微镜检查,费时且容易出现误差。通过深度学习技术,特别是目标检测模型YOLO,可以实现自动化、快速且准确的血细胞检测和分…...

鸿蒙Flex布局
效果: 代码: 换行代码参数设置: wrap:FlexWrap.Wrap Entry Component struct FlexCase {State message: string Hello World;build() {Flex({direction:FlexDirection.Row,justifyContent:FlexAlign.SpaceAround,alignItems:ItemAlign.Cen…...

开发自己的 Web 框架
开发自己的 Web 框架 开发Web服务器主体程序开发Web框架程序使用模板来展示响应内容开发框架的路由列表功能采用装饰器的方式添加路由电影列表页面的开发案例 接收web服务器的动态资源请求,给web服务器提供处理动态资源请求的服务。根据请求资源路径的后缀名进行判断…...
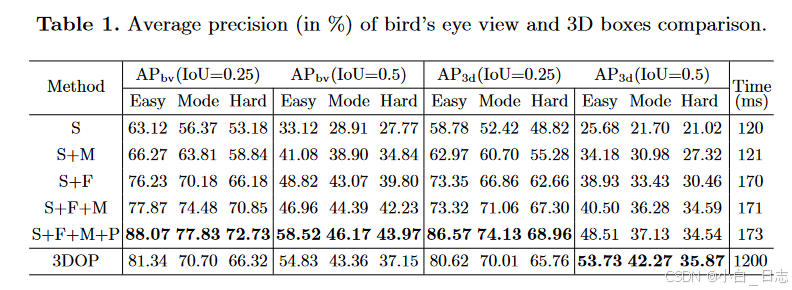
用于自动驾驶的基于立体视觉的语义 3D 对象和自我运动跟踪
Stereo Vision-based Semantic 3D Object and Ego-motion Tracking for Autonomous Driving 论文 摘要: 我们提出了一种基于立体视觉的方法,用于在动态自动驾驶场景中跟踪相机自我运动和 3D 语义对象。我们建议使用易于标记的 2D 检测和离散视点分类以及…...
Spring@Autowired注解
Autowired顾名思义,就是自动装配,其作用是为了消除代码Java代码里面的getter/setter与bean属性中的property。当然,getter看个人需求,如果私有属性需要对外提供的话,应当予以保留。 因此,引入Autowired注解…...

32.x86游戏实战-使用物品call
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 本次游戏没法给 内容参考于:微尘网络安全 工具下载: 链接:https://pan.baidu.com/s/1rEEJnt85npn7N38Ai0_F2Q?pwd6tw3 提…...
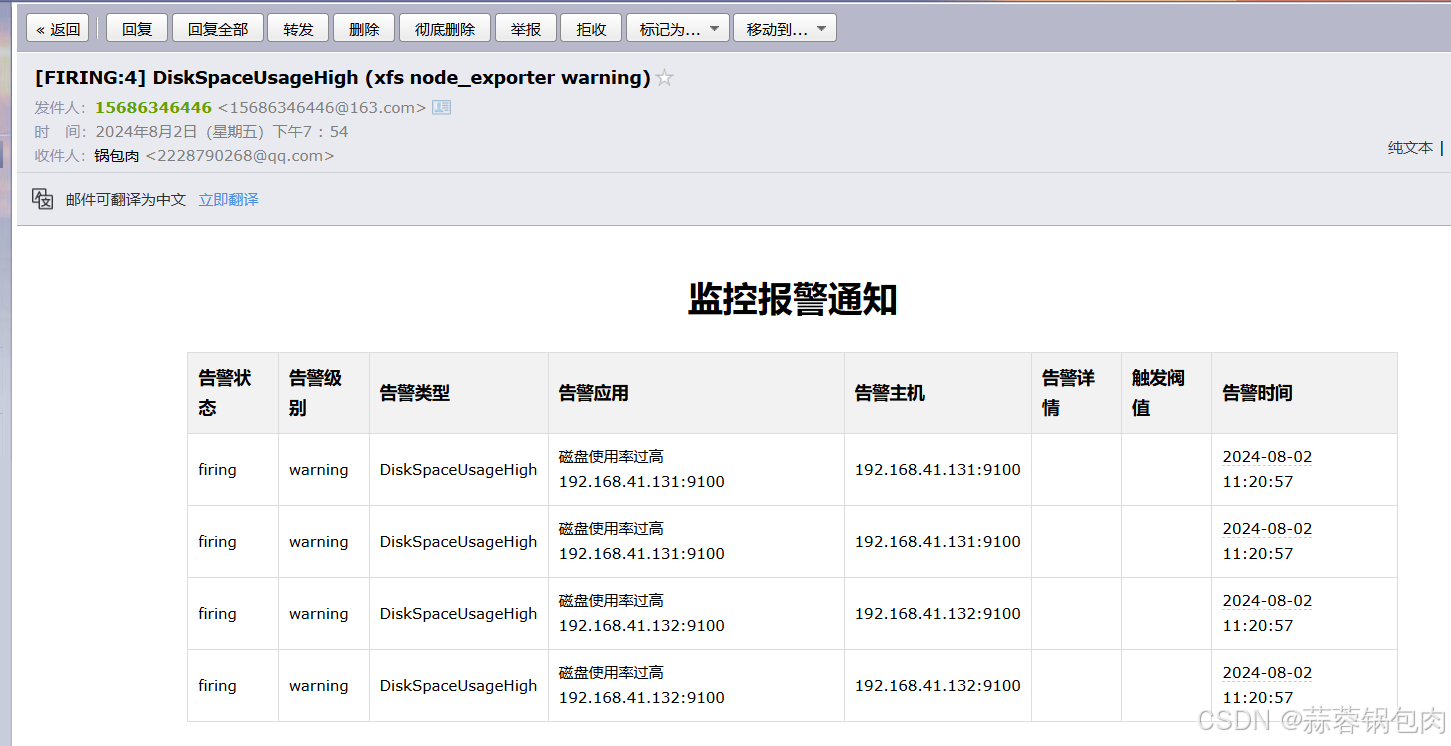
Prometheus+Alertmanager+邮件告警
参考node_exporter-CSDN博客,球球不要断更!!!! 大致流程 1.部署promethus 可以写一个自定义的 systemd 服务启动文档,详情见自定义的 systemd 服务启动方式-CSDN博客 [rootlocalhost system]# sudo tee /e…...
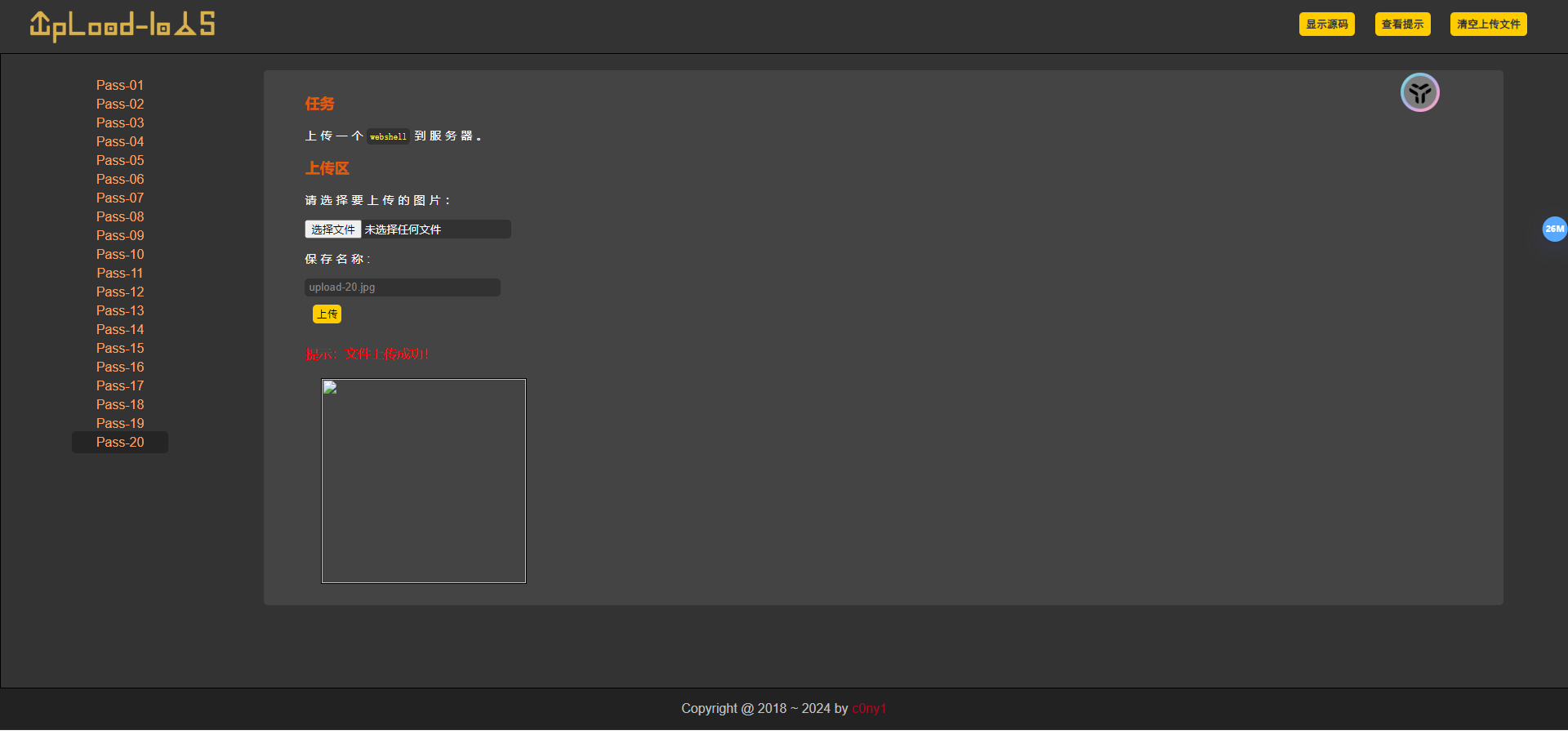
upload-labs漏洞靶场~文件上传漏洞
寻找测试网站的文件上传的模块,常见:头像上传,修改上传,文件编辑器中文件上传,图片上传、媒体上传等,通过抓包上传恶意的文件进行测试,上传后缀名 asp php aspx 等的动态语言脚本,查…...

PostgreSQL 高阶函数详解:全面深入的功能与实用示例
PostgreSQL 高阶函数详解 PostgreSQL 是一款功能强大的开源关系数据库管理系统,以其丰富的功能和高扩展性著称。在数据处理和分析方面,PostgreSQL 提供了一系列高阶函数,可以极大地简化和优化各种复杂操作。本文将详细介绍 PostgreSQL 的高阶…...

Redis——集合 SET
目录 1. 添加元素 SADD 2. 查看元素 SMEMBERS 3. 判断元素是否存在该集合 SISMEMBER 4. 删除元素 SREM 集合 SET 是一种无序集合;因此其与列表有以下区别: (1)列表是有序的,集合是无序的; ࿰…...

openEuler安装docker
1.下载地址 搜索docker 寻找docker-ce 复制地址 2.配置仓库 [rootlocalhost yum.repos.d]# pwd /etc/yum.repos.d [rootlocalhost yum.repos.d]# vim docker-ce.repo [docker-ce] namedocker baseurlhttps://mirrors.aliyun.com/docker-ce/linux/rhel/9/x86_64/stable/ gpgche…...
- 缺失值)
每天一个数据分析题(四百六十五)- 缺失值
某连续型变量的数据集存在缺失值,可以采用哪种方法处理? A. 插值法填补 B. EM算法填补 C. 随机森林填补 D. 以上均不对 数据分析认证考试介绍:点击进入 题目来源于CDA模拟题库 点击此处获取答案 数据分析专项练习题库 内容涵盖Pytho…...
干货 | 变频器的详细介绍
变频器简述 变频器是电机控制领域中常见的一种设备,也称变频调节器,是一种将固定频率的交流电转换为可调频率的交流电的电力电子设备,用于控制交流电机的转速和输出功率。变频器通过调节输出电源的电压和频率,从而控制电动机的转速…...

Linux线程2
线程相关函数 线程分离--pthread_detach(后面会详细讲) 函数原型:int pthread_datach(pthread_t thread); 调用该函数之后不需要 pthread_join 子线程会自动回收自己的PCB 杀死(取消)线程--pthread_cancel 取…...

乱弹篇(40)人类追求长寿
不要认为只有中国的老龄化才严重,实际上全球都面临老龄化,其中日本最为严重。 这是随着人类生活和医学水平的不断提高,寿命才会比过去数十年有了大幅度的提升。据资料显示,目前全球平均预期寿命估计为73岁。与百年之前相比&#…...

技术详解:互联网医院系统源码与医保购药APP的整合开发策略
本篇文章,小编将从系统架构、数据安全、用户体验和技术实现等方面详细探讨互联网医院系统与医保购药APP的整合开发策略。 一、系统架构 1.模块化设计 互联网医院系统与医保购药APP的整合需要采用模块化设计。 2.微服务架构 每个功能模块作为一个独立的微服务&am…...

N4 - Pytorch实现中文文本分类
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 目录 任务描述步骤环境设置数据准备模型设计模型训练模型效果展示 总结与心得体会 任务描述 在上周的任务中,我们使用torchtext下载了托管的英文的…...

centos 如何安装sox音视频处理工具
要在 CentOS 系统上安装 Sox 音频处理软件,你可以遵循以下步骤。请注意,这些说明适用于 CentOS 7,对于 CentOS 8 及更高版本,某些包管理命令可能略有不同。 第一步:安装所需的依赖库 首先,你需要安装一系列…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...
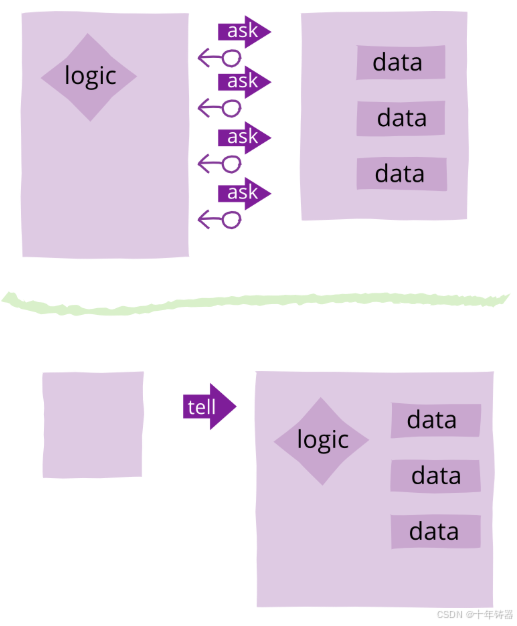
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...
