快速傅里叶算法(FFT)快在哪里?
目录
前言
1、DFT算法
2、FFT算法
2.1 分类
2.2 以基2 DIT(时间抽取) FFT 算法为例
2.2.1 一次分解
2.2.2 多次分解
参考
前言
对信号分析的过程中,为了能换一个角度观察问题,很多时候需要把时域信号波形变换到频域进行分析,这涉及到对信号求傅里叶变换,在计算机中便于处理的是离散信号,因此需要求信号的离散傅里叶变换,但是离散傅里叶变换(DFT--Discrete Fourier transform)的算法时间复杂度O(n2),为了能提高计算的速度,很多时候我们进行的变换为快速傅里叶变换(FFT--Fast Fourier Transform),其算法时间复杂度O(nlogn),大大提高了计算的速度,那么该快速傅里叶变换算法的快在哪里?中间进行了什么操作,我们下面具体分析。
在之前的一篇文章中我们提到了DFT和FFT的关系
频谱、功率谱、倒频谱_heda3的博客-CSDN博客_倒频谱
1、DFT算法
DFT的数学计算表达式为:
长度为N的离散时间信号x(n),做N点离散傅里叶变换如下:
其中k=0,1,2,...N-1
其中
运算量表述为:
依据上述公式可知,做1点DFT,需要N次复数乘法、N-1次复数加法
做N点DFT,则需要N*N次复数乘法、N*(N-1)次复数加法
当N为256点时,所需运算量65536次复数乘法、65280次复数加法
N=512点时,所需运算量262144次复数乘法、261632次复数加法
N=1024点时,所需运算量1048576次复数乘法、1047552次复数加法
可见当N点从256到1024点变化时,DFT算法的计算量从万级到百万级。
2、FFT算法
2.1 分类
分为按照时间抽取(在时间上将信号长度逐步减少)和按照频率抽取
依据抽取长度分为基2、基4
基2 DIT(时间抽取) FFT 也称为Cooley-Tukey algorithm 库利图基算法
基2 DIF(频率抽取) FFT
基4 FFT
分裂基FFT(包含两种不同基的混合计算)
2.2 以基2 DIT(时间抽取) FFT 算法为例
基于基2时间抽取将信号划分为两部分分别计算FFT(信号长度N要求为N=2的整数倍):
1)
其中k=0,1,2,...N-1
复数运算的特性
对称性:
周期性:
可约性:
常见的计算
2.2.1 一次分解
依据上述复数运算的特性的可约性,则1)化简为:
2)
3)
其中k=0,1,2,...N-1
利用特性:
则3)可表述为:
4)
其中k=0,1,2,...N/2-1
用如下的蝶形方式表述为3式和4式:
两次复数运算:
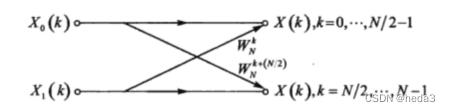
一次复数运算:
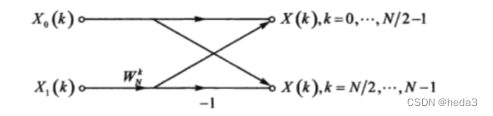
也即是N点DFT包含:2个 N/2点DFT和N/2个蝶形运算,一个蝶形运算包含一次复数乘法和两次复数加法
上述:做N点DFT,则需要N*N次复数乘法、N*(N-1)次复数加法
则2个N/2点DFT,则需要2*(N/2*N/2)=/2次复数乘法,2*(N/2)*(N/2-1)=N(N/2-1)次复数加法运算;蝶形运算次数:N/2次复数乘法,N次复数加法。
因此总的复数乘法计算:N(N+1)/2 总的复数加法次数:/2
通过上述的一次分解前后的运算量分析,可见经过一次分解后(信号按照奇偶数将N点DFT划分为N/2点DFT,并将两个N/2点DFT组合的方式),其运算量降低了一半,计算效率得到了提升。
2.2.2 多次分解
当N一直分解下去直到DFT的点数为2时,最小的计算单元为一个基本的蝶形运算,因此由于信号长度最初定义为N=2的整数倍,也即是N=,因此N点DFT运算可以分解为M级蝶形运算,每一级为N/2个蝶形运算。
通过上述的FFT计算方法,则N点FFT运算需要M*N/2个蝶形运算,复数乘法次数:
复数加法次数:
当N点从256到1024点变化时,FFT算法的计算量从千级到万级。可见FFT运算速度较DFT得到较大的提升。
现在我们可以明显知道FFT到底快在哪里,因为经过对信号的逐级分解,将大点DFT划分为小点DFT计算,也即是N点FFT若基于基2抽取方法,则需要级分解,N点DFT最终划分为2点DFT计算,并结合指数运算的特性,减少冗余计算,使得运算量大为减小。
参考
【1】《数字信号处理》
【2】如何利用FFT(基2时间以及基2频率)信号流图求序列的DFT
相关文章:
快速傅里叶算法(FFT)快在哪里?
目录 前言 1、DFT算法 2、FFT算法 2.1 分类 2.2 以基2 DIT(时间抽取) FFT 算法为例 2.2.1 一次分解 2.2.2 多次分解 参考 前言 对信号分析的过程中,为了能换一个角度观察问题,很多时候需要把时域信号波形变换到频域进行分…...

利用Markdown写学术论文资料汇总贴
1是最详细的,重点看! Markdown 写作,Pandoc 转换:我的纯文本学术写作流程 2补充一些细节,也可以看看。 用Markdown写作学术论文 3写得和上面差不多,如果上面两篇有什么问题还没解决,可以看看…...
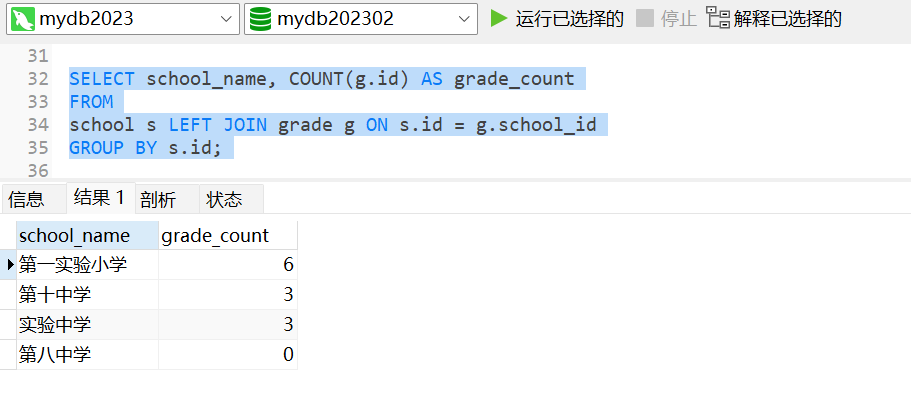
MySQL 高级查询
目录1.左关联2.右关联3.子查询4.联合查询5.分组查询1.左关联 MySQL中的左关联(Left Join)是一种基于共同列的连接操作, 它将左侧表中的所有行与右侧表中匹配的行结合在一起, 如果右侧表中没有匹配的行,则结果集中右侧…...
JavaSE学习day4_01 循环for,while,do...while
1. 循环高级 1.1 无限循环 for、while、do...while都有无限循环的写法。 最为常用的是while格式的。 因为无限循环是不知道循环次数的,所以用while格式的 代码示例: while(true){} 1.2 跳转控制语句(掌握) 跳转控制语句&…...

C/C++中的static关键字
概述在C/C中都有static关键字的使用,可以分别修饰变量和函数,分为静态变量【静态成员】、静态成员函数。2. static用法概况静态变量的作用范围在一个文件内,程序开始时分配空间,结束时释放空间,默认初始化为0ÿ…...

67 自注意力【动手学深度学习v2】
67 自注意力【动手学深度学习v2】 深度学习学习笔记 学习视频:https://www.bilibili.com/video/BV19o4y1m7mo/?spm_id_fromautoNext&vd_source75dce036dc8244310435eaf03de4e330 给定长为n 的序列,每个xi为长为d的向量,自注意力将xi 既当…...
电子学会2022年12月青少年软件编程(图形化)等级考试试卷(二级)答案解析
青少年软件编程(图形化)等级考试试卷(二级) 一、单选题(共25题,共50分) 1. 一个骰子,从3个不同角度看过去的点数如图所示,请问5的对面是什么点数?( ) …...

关于链表中插入结点的操作……
服了,好久没敲链表了,这都忘了 newnode->next cur->next; cur->next newnode; newnode->next cur->next; cur->next newnode; newnode->next cur->next; cur->next newnode; newnode->next cur->next; cur-…...
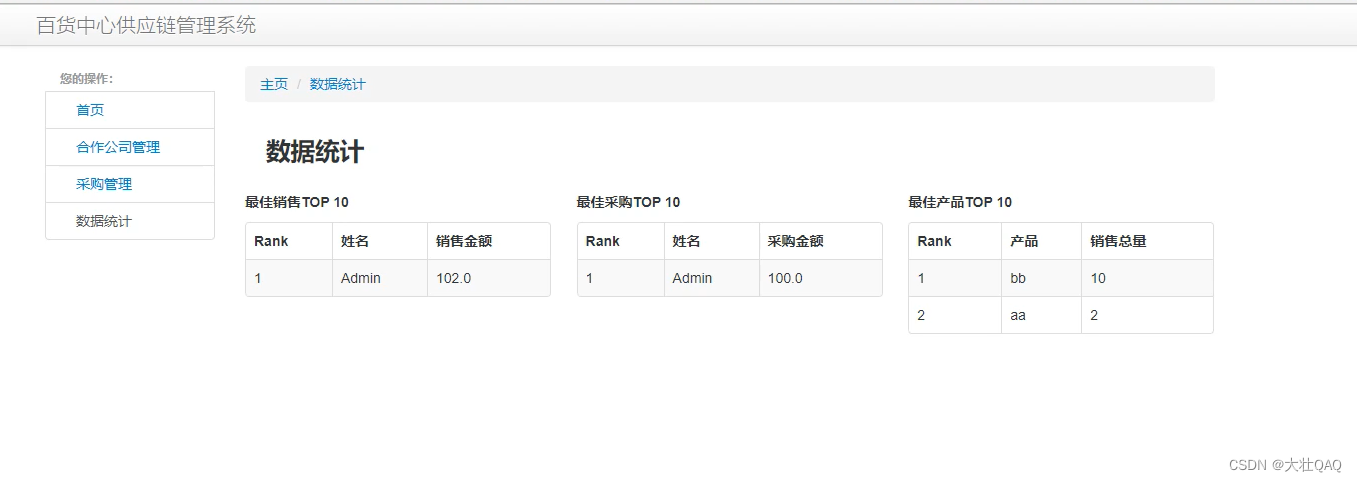
【项目精选】百货中心供应链管理系统
点击下载源码 近年来,随着计算机技术的发展,以及信息化时代下企业对效率的需求,计算机技术与通信技术已经被越来越多地应用到各行各业中去。百货中心作为物流产业链中重要的一环,为了应对新兴消费方式的冲击,从供货到销…...
Qt优秀开源项目之十六:SQLite数据库管理系统—SQLiteStudio
首先,感谢CSDN官方认可 SQLiteStudio是一款开源、跨平台(Windows、Linux和MacOS)的SQLite数据库管理系统。 github地址:https://github.com/pawelsalawa/sqlitestudio 官网:https://sqlitestudio.pl/ 特性很多…...

Python __doc__属性:查看文档
在使用 dir() 函数和 __all__ 变量的基础上,虽然我们能知晓指定模块(或包)中所有可用的成员(变量、函数和类),比如:import string print(string.__all__)程序执行结果为:[ascii_lett…...
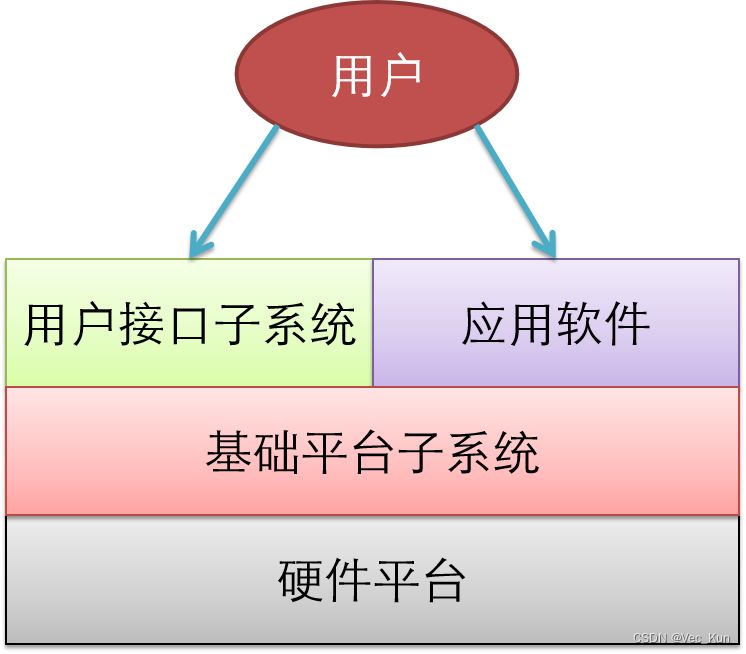
电子科技大学操作系统期末复习笔记(一):操作系统概述
目录 前言 操作系统概述 操作系统的目标与功能 操作系统的定义 目标 功能 操作系统的历史 单用户系统 简单批处理系统 多道批处理系统 分时系统 个人电脑 → 分布式系统 → 互联网时代 → 移动计算时代 → ...... 实时系统 操作系统的基本特征 并发 共享 虚拟…...
)
[实践篇]13.20 Qnx进程管理slm学习笔记(三)
【QNX Hypervisor 2.2用户手册】目录(完结) 4.2 模块 我们可以将组件组合成一个模块。模块中的进程可以组成一个子系统,也可以用于建立一组系统状态,例如基本操作和各种更高级别操作。注意,必须命名模块,以便可以在内部引用它们。而且每个模块必须描述成一个元素,形势如…...
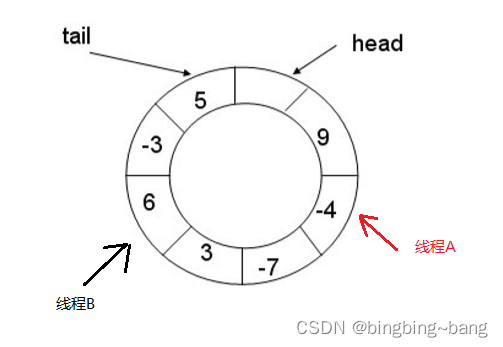
冰冰学习笔记:多线程
欢迎各位大佬光临本文章!!! 还请各位大佬提出宝贵的意见,如发现文章错误请联系冰冰,冰冰一定会虚心接受,及时改正。 本系列文章为冰冰学习编程的学习笔记,如果对您也有帮助,还请各位…...

补充一些前端面试题
javascript有哪些库指路>js中的库uniapp和vue有什么区别什么是uniappuni-app(uni,读you ni,是统一的意思)是一个使用Vue.js开发所有前端应用的框架,开发者编写一套代码,可发布到iOS、Android、Web&#…...

七大设计原则之单一职责原则应用
目录1 单一职责原则介绍2 单一职责原则应用1 单一职责原则介绍 单一职责(Simple Responsibility Pinciple,SRP)是指不要存在多于一个导致类变更的原因。假设我们有一个 Class 负责两个职责,一旦发生需求变更,修改其中…...

[USACO23JAN] Leaders B
题面翻译 题面描述 FJ 有 NNN 头奶牛,每一头奶牛的品种是根西岛 G 或荷斯坦 H 中的一种。 每一头奶牛都有一个名单,第 iii 头奶牛的名单上记录了从第 iii 头奶牛到第 EiE_iEi 头奶牛的所有奶牛。 每一种奶牛都有且仅有一位“领导者”,对…...
C++模板初阶
C模板初阶泛型编程函数模板概念函数模板格式函数模板原理函数模板的实例化模板参数的匹配原则类模板类模板的定义格式类模板的实例化泛型编程 我们前面学习了C的函数重载功能,那么我们如何实现一个通用的交换函数呢,比如:我传入int就是交换intÿ…...

文献阅读:Scaling Instruction-Finetuned Language Models
文献阅读:Scaling Instruction-Finetuned Language Models 1. 文章简介2. 实验 1. 数据集 & 模型 1. 数据集考察2. 使用模型 2. scale up对模型效果的影响3. CoT对模型效果的影响4. 不同模型下Flan的影响5. 开放接口人工标注指标 3. 结论 文献链接:…...

gpt草稿
ChatgptWhatChatGPT(全名:Chat Generative Pre-trained Transformer [2])是由OpenAI开发的一个人工智能聊天机器人程序,于2022年11月推出。该程序使用基于GPT-3.5架构的大型语言模型并通过强化学习进行训练。ChatGPT里面有两个词&…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
