C语言基础知识之函数指针和指针函数
函数指针和指针函数
- 函数指针和指针函数
- 指向函数的指针
- 返回指针值的函数
- 指针函数和函数指针的区别
- 问题1_1
- 代码1_1
- 结果1_1
函数指针和指针函数
指向函数的指针
用函数指针变量调用函数
可以用指针变量指向整型变量、字符串、数组,也可以指向一个函数。一个函数在编译时被分配给一个入口地址。这个函数的入口地址就称为函数的指针。
函数指针变量常用的用途之一是把指针作为参数传递到其他函数。
类型名 ( ∗ 函数名 ) (参数表列) ; 类型名 (*函数名)(参数表列); 类型名(∗函数名)(参数表列);
例如:
i n t ( ∗ a ) ( i n t x , i n t y ) ; int\ (*\ a)(int\ x, int\ y); int (∗ a)(int x,int y);
返回指针值的函数
一个函数可以带回一个整型值、字符值、实型值等,也可以带回指针型的数据,即地址。其概念与以前类似,只是带回的值的类型是指针类型而已。这种带回指针值的函数,一般定义形式为:
类型名 ∗ 函数名(参数表列) ; 类型名 *函数名(参数表列); 类型名∗函数名(参数表列);
例如:
i n t ∗ a ( i n t x , i n t y ) ; int\ *\ a(int\ x, int\ y); int ∗ a(int x,int y);
指针函数和函数指针的区别
这两个概念都是简称:
指针函数是指带指针的函数,即本质是一个函数。
函数指针是指向函数的指针变量,因而函数指针本身首先应是指针变量,只不过该指针变量指向函数。
问题1_1
函数 f u n fun fun的功能是:用函数指针指向要调用的函数,并进行调用。
代码1_1
#include<stdio.h>double f1(double x){return x*x;
}double f2(double x, double y){return x*y;
}double fun(double a, double b){double (*f)();double r1, r2;f = f1;r1 = f(a);f = f2;r2 = (*f)(a, b);return r1+r2;
}void main(void){double x1=5, x2=3, r;r = fun(x1, x2);printf("\nx1 = %f, x2 = %f, x1*x1 + x1*x2 = %f\n", x1, x2, r);
}
结果1_1

相关文章:

C语言基础知识之函数指针和指针函数
函数指针和指针函数 函数指针和指针函数指向函数的指针返回指针值的函数指针函数和函数指针的区别 问题1_1代码1_1结果1_1 函数指针和指针函数 指向函数的指针 用函数指针变量调用函数 可以用指针变量指向整型变量、字符串、数组,也可以指向一个函数。一个…...

【Unity】web gl inputFied 中文输入,同时支持TextMeshInputFied,支持全屏
同时支持TextMeshInputFied,支持全屏。 使用github包【WebGLInput】:https://github.com/kou-yeung/WebGLInput 需要资源的在这里也可以下载 https://download.csdn.net/download/weixin_46472622/89600795 用于unity web gl 中文输入,只需…...

vue3+vite全局引入less变量和函数
需要在vite配置 plugins: [css: {preprocessorOptions: {less: {additionalData: import "./src/styles/variables.module.less"; import "./src/views/Visualization/component/ViewportCom/px2viewport.less";,javascriptEnabled: true}}}, ]多个文件按…...

H81002S 1.7mm网络变压器:BMS汽车蓝牙接收器中的超薄共模电感科技
华强盛导读:在当今这个日新月异的汽车科技领域,每一处细节都蕴含着创新与突破。作为电动汽车心脏的电池管理系统(BMS),其高效稳定的运行不仅关乎续航与安全,更是智能化驾驶体验的基石。而在这背后ÿ…...

C语言.回调函数
回调函数 回调函数也是一个函数。与一般函数直接调用区别在于,使用回调函数的过程,是一个函数将另一个函数作为参数调用。而被用来调用的那个函数,就是回调函数。 回调函数就是一个通过函数指针调用的函数。如果你把函数的指针(地…...

《从零开始:使用Python构建简单Web爬虫》
前言 随着互联网信息的爆炸性增长,如何高效地获取和处理这些数据变得越来越重要。Web爬虫作为一种自动化工具,可以帮助我们快速抓取所需的网页内容。本文将介绍如何使用Python编写一个简单的Web爬虫,并通过实例演示其基本用法。 准备工作 …...

最新个人免签约支付系统源码|PHP源码 | 码支付系统 | ThinkPHP6框架 | 开源
源码介绍: 这个最新的个人专用免签约支付系统源码!是PHP源码写的哦,而且是用ThinkPHP6框架开发的,完全开源的码支付系统。 这个系统适合个人用户使用,作为收款的免签约解决方案。它还加入了监控端,可以拒…...

The Llama 3 Herd of Models 第4部分后训练的全文
Llama 3前三部分包括介绍、总体概述和预训练https://blog.csdn.net/qq_51570094/article/details/140682445?spm=1001.2014.3001.5501 4 Post-Training 后训练 我们通过应用几轮后训练6或将模型与人类反馈对齐来生成对齐的Llama 3模型(Ouyang等人,2022;Rafailov等人,2024)在…...

MongoDB性能调优
文章目录 MongoDB性能调优MongoDB性能不佳原因影响MongoDB性能的因素MongoDB性能监控工具mongostatmongotopProfiler模块db.currentOp() MongoDB性能调优 MongoDB性能不佳原因 慢查询阻塞等待硬件资源不足 1,2通常是因为模型/索引设计不佳导致的 排查思路:按1-2…...

【Qt开发】调试log日志QDebug重定向输出到textEdit等控件(qInstallMessageHandler回调函数)
【Qt开发】调试log日志QDebug重定向输出到textEdit等控件(qInstallMessageHandler回调函数) 文章目录 Log输出方式qInstallMessageHandler回调函数线程安全textEdit控件附录:C语言到C的入门知识点(主要适用于C语言精通到Qt的C开发…...

【JavaEE精炼宝库】 网络编程套接字——UDP业务逻辑 | TCP流套接字编程及业务逻辑实现
文章目录 一、UDP业务逻辑实现二、TCP流套接字编程2.1 API 介绍:2.1.1 ServerSocket:2.1.2 Socket: 2.2 Java流套接字通信模型:2.3 代码示例:2.3.1 TCP Echo Server:2.3.2 TCP Echo Client:2.3.…...

前端过渡动画
前端过渡动画 vue3 1、组件进入视口时向上移动且渐显 1、创建js文件addViewportEffect.js function slideDownEffect(element) {console.log("执行");element.style.transform translateY(0);element.style.opacity 1; }/*** 添加视口效果到指定的类名元素上。…...

actual combat 38 ——vue
vue-cli脚手架 创建命令:vue create 项目名称 eslint 如何关闭? vue.config.js文件中加 module.exports {lintOnSave: false }文件全代码: const { defineConfig } require(vue/cli-service) module.exports defineConfig({transpile…...
— 功能测试用例一般包含哪些内容)
测试面试宝典(四十七)— 功能测试用例一般包含哪些内容
首先,明确测试用例的编号和名称,以便于识别和管理。 其次,详细描述测试的目标和背景,让其他人能够清楚了解该测试用例的目的和适用场景。 接着是测试的步骤,需要清晰、准确地列出每一个操作步骤,包括输入…...

rust_mac环境安装
在 macOS 上安装 Rust 很简单。你可以使用 Rust 提供的安装工具 rustup。下面是安装步骤: 打开终端。 运行以下命令以安装 rustup 和 Rust: curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh按照提示进行操作: 这个命令将下载并…...

【前端面试】七、算法-递归
常考算法 排序算法:快速排序、归并排序、堆排序等。 查找算法:二分查找、哈希表查找等。 动态规划:解决最优化问题,如斐波那契数列、最长公共子序列等。 图论算法:最短路径(Dijkstra、Floyd-Warshall&am…...

CmsEasy逻辑漏洞--零元购
CmsEasy逻辑漏洞--零元购 选择购买MackBook 购买成功后会员中心发现多出8100快钱 然后就可以正常购买了...

Linux 内核源码分析---I/O 体系结构与访问设备
I/O 体系结构 与外设的通信通常称之为输入输出,一般都缩写为I/O。 在实现外设的I/O时,内核必须处理3个可能出现的问题: (1)必须根据具体的设备类型和模型,使用各种方法对硬件寻址; (…...
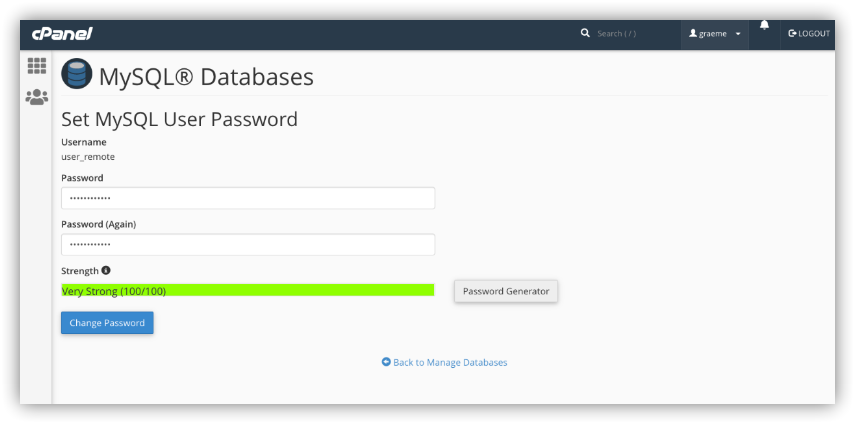
在cPanelWHM中如何重置 MySQL 用户帐户密码
更改MySQL用户账户密码非常简单。服务器管理员可以在WHM中编辑任何MySQL用户的帐户。cPanel用户可以编辑其帐户管理的数据库的密码。 在WHM中更改MySQL用户帐户密码 打开WHM,在侧边菜单中的SQL服务下选择“Change MySQLUser Password”。Hostease的服务器产品提供稳…...

软件测试基础1--功能测试
1、什么是软件测试? 软件是控制计算机硬件运行的工具。 软件测试:使用技术手段验证软件是否满足使用需求,为了发现软件功能和需求不相符合的地方,或者寻找实际输出和预期输出之间的差异。 软件测试的目的:减少软件缺陷…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...

VSCode 没有添加Windows右键菜单
关键字:VSCode;Windows右键菜单;注册表。 文章目录 前言一、工程环境二、配置流程1.右键文件打开2.右键文件夹打开3.右键空白处打开文件夹 三、测试总结 前言 安装 VSCode 时没有注意,实际使用的时候发现 VSCode 在 Windows 菜单栏…...
