计算机常识与NOIP历史-CSP初赛知识点整理






 真题练习
真题练习
[2021-CSP-J-第2题]
以下奖项与计算机领域最相关的是( )。
A.奥斯卡奖 B.图灵奖 C.诺贝尔奖 D.普利策奖
[2017-NOIP-第7题]
中国计算机学会于( )年创办全国青少年计算机程序设计竞赛。
A. 1983 B. 1984 C. 1985 D. 1986
[2018-NOIP-第5题]
NOI 的中文意思是( )。
A. 中国信息学联赛
B. 全国青少年信息学奥林匹克竞赛
C. 中国青少年信息学奥林匹克竞赛
D. 中国计算机协会
真理解析
[2021-CSP-J-第2题]
以下奖项与计算机领域最相关的是( 图灵奖 )。
A.奥斯卡奖 B.图灵奖 C.诺贝尔奖 D.普利策奖
题解:
A. 奥斯卡奖:
奥斯卡奖,全称美国电影艺术与科学学院奖(Academy Awards),是美国电影界的最高奖项,表彰在电影艺术和技术方面的杰出贡献。这一奖项主要关注电影制作和表演艺术,与计算机领域无直接关联。
B. 图灵奖:
图灵奖(Turing Award),由美国计算机协会(ACM)于1966年设立,专门奖励那些对计算机事业作出重要贡献的个人。这个奖项的名字来自计算机科学的先驱艾伦·麦席森·图灵,他对计算机科学、密码学、逻辑学和人工智能等领域都有深远影响。图灵奖是计算机领域的最高奖项,与计算机领域高度相关。
C. 诺贝尔奖:
诺贝尔奖是根据阿尔弗雷德·诺贝尔的遗愿所设立的奖项,包括物理学奖、化学奖、生理学或医学奖、文学奖以及和平奖。虽然这些奖项涵盖了多个重要领域,但并未特别针对计算机或信息技术领域设立奖项。
D. 普利策奖:
普利策奖是根据约瑟夫·普利策的遗愿设立的,主要奖励在新闻、文学和音乐领域的杰出贡献。这一奖项与计算机领域没有直接联系。
综上所述,与计算机领域最相关的奖项是图灵奖,因为它专门奖励在计算机事业中作出重要贡献的个人。
因此,答案是B.图灵奖。
[2017-NOIP-第7题]
中国计算机学会于(1984 )年创办全国青少年计算机程序设计竞赛。
A. 1983 B. 1984 C. 1985 D. 1986
题解:中国计算机学会于1984年创办全国青少年计算机程序设计竞赛(简称:NOI)。NOI作为国内信息学领域面向中学生的最高水平的大赛,其系列活动包括全国青少年信息学奥林匹克竞赛(NOI)、全国青少年信息学奥林匹克联赛(NOIP)、全国青少年信息学奥林匹克竞赛冬令营(WC)和国际信息学奥林匹克中国队选拔赛(CTS)等。这些活动为中学生提供了一个展示自己计算机程序设计能力的平台,同时也促进了我国信息学教育的发展。正确答案是B. 1984。
[2018-NOIP-第5题]
NOI 的中文意思是(B )。
A. 中国信息学联赛
B. 全国青少年信息学奥林匹克竞赛
C. 中国青少年信息学奥林匹克竞赛
D. 中国计算机协会
题解:NOI,全称 National Olympiad in Informatics,是面向中学生的全国性的计算机程序设计竞赛,旨在普及计算机科学知识,给学校的信息技术教育课程提供动力和新的思路,给那些有才华的学生提供相互交流和学习的机会,通过竞赛和相关的活动培养和选拔优秀计算机人才。这一竞赛在中国由中国计算机学会主办,是信息学领域面向中学生的最高水平的大赛。
相关文章:

计算机常识与NOIP历史-CSP初赛知识点整理
真题练习 [2021-CSP-J-第2题] 以下奖项与计算机领域最相关的是( )。 A.奥斯卡奖 B.图灵奖 C.诺贝尔奖 D.普利策奖 [2017-NOIP-第7题] 中国计算机学会于( )年创办全国青少年计算机程序设计竞赛。 A. 1983 B. 1984 C. 1985 D. 1986 [2018-NOIP-第5题…...

代码随想录算法训练营第二天 | 209. 长度最小的子数组、59. 螺旋矩阵 II
目录 209. 长度最小的子数组1、题目描述2、思路3、code4、复杂度分析 LC59 螺旋矩阵 II1、题目描述2、思路3、code4、复杂度分析 209. 长度最小的子数组 题目链接:209 1、题目描述 给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于…...
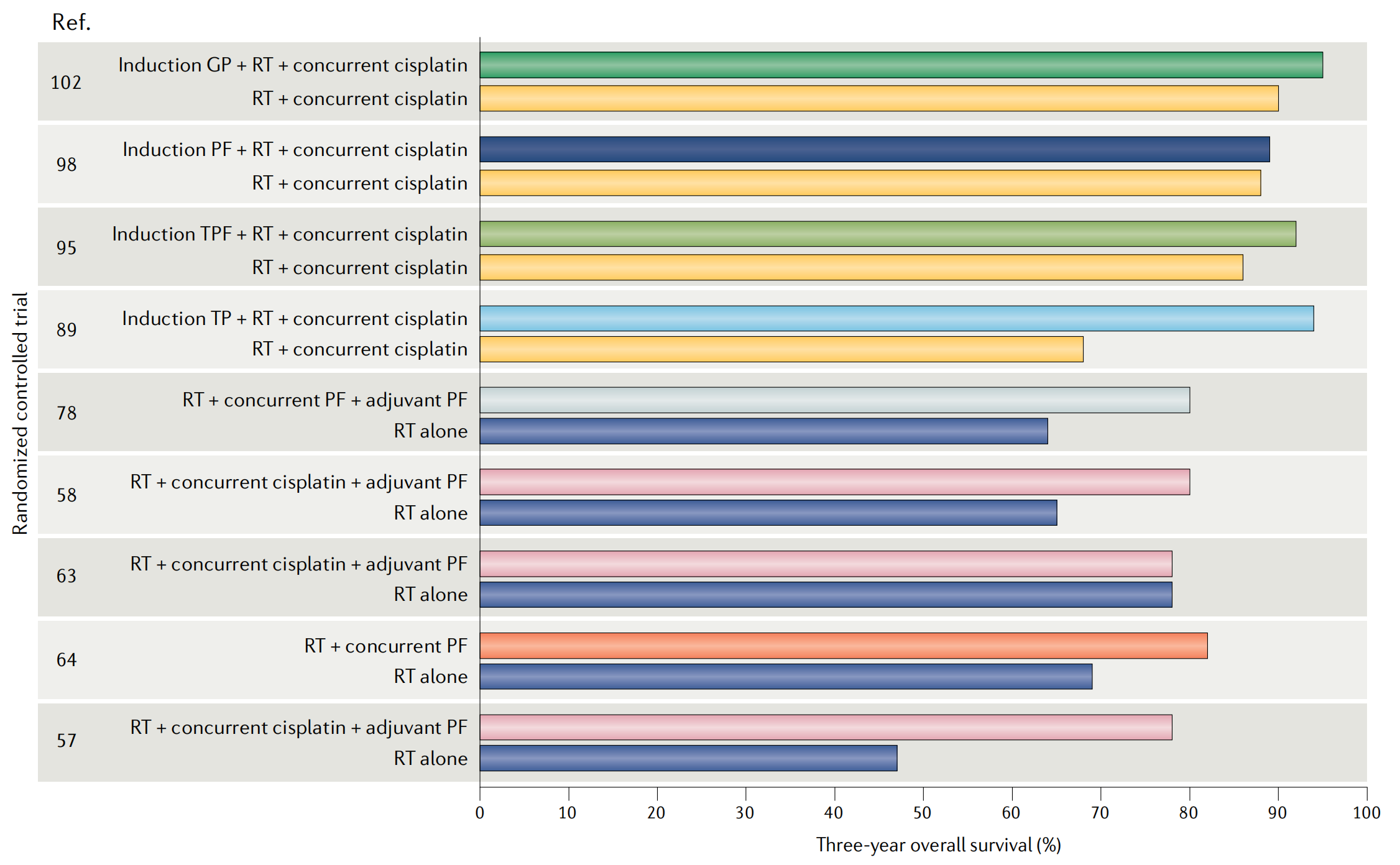
鼻咽癌综述
小罗碎碎念 本期推文主题:鼻咽癌综述 这篇文章提供了一个全面的综述,探讨了鼻咽癌(NPC)的关键研究进展,包括病理机制、治疗、筛查和生物标志物的发展。 文章首先强调了NPC在特定地理区域的流行情况,并讨论了…...

中国AI PC行业研究报告
核心摘要: 2020-2023年中国笔电出货量呈下降趋势,PC厂商亟需从产品形态、软硬技术、需求场景等角度寻求新的增长机会。而随着大模型、生成式AI技术的到来,其强大的数据处理、学习泛化与内容生成能力,高质效加速了各行各业人工智能…...

Mybatis实战:图书管理系统(笔记)
前言:如果在接口的声明方法中鼠标右键没有Test的单元测试。 你的鼠标光标问题:要在花括号范围内!!!! 数据库表是应⽤程序开发中的⼀个重要环节, 数据库表的设计往往会决定我们的应⽤需求是否能顺利实现, 甚…...

win11 amd64 python安装matplotlib、pytorch报错记录
win11 amd64 python matplotlib 安装报错记录 安装时 错误是 metadata-generation-failed 查看上面的具体报错原因,来自: Files\Python\Python3_10_11\Include: linker input file not found: No such file or director注意Python 的路径中最好不要有…...
)
Python写UI自动化--playwright(等待页面加载机制)
很多情况下,我们都需要等待页面加载到一定程度才能进行下一步操作,而这个度该怎么操作,这篇文章就来详细讲一讲 目录 expect_popup() wait_until参数 "load" commit: "domcontentloaded" "networkidle"…...
0804)
书籍将整数字符串转成整数值(5)0804
题目 给定一个字符串str,如果str符合日常书写的整数形式,并且属于32位整数的范围,返回str所代表的整数值,否则返回0。 举例 str“123” 返回 123 str“023” 因为023 不符合日常的书写习惯,所以返回0 str“A13” …...

【2024年华数杯C题老外游中国】(完整题解+代码+完整参考论文)
请问 352 个城市中所有 35200 个景点评分的最高分(Best Score,简称 BS)是多少?全国有多少个景点获评了这个最高评分(BS)?获评了这个最高评分(BS)景点最多的城市有哪些&am…...

全球氢化双酚A (HBPA)市场规划预测:2030年市场规模将接近1330亿元,未来六年CAGR为2.7%
一、引言 随着全球化工行业的持续发展,氢化双酚A (HBPA)作为重要的化工原料,其市场重要性日益凸显。本文旨在探索HBPA行业的发展趋势、潜在商机及其未来展望。 二、市场趋势 全球HBPA市场的增长主要受全球化工行业增加、消费者对高性能化工产品要求提高…...

【C++】异常处理:深度解析与实战精髓,不容错过的编程秘籍
🌈 个人主页:Zfox_ 🔥 系列专栏:C从入门到精通 目录 🚀 前言:C语言传统的处理错误的方式 一: 🔥 C异常概念二: 🔥 异常的使用 2.1 📖 异常的抛出和…...

智能指针的循环引用 是什么 怎么引起的
智能指针的循环引用 是什么 怎么引起的 智能指针的循环引用(Circular Reference)是指两个或多个对象之间的共享指针相互引用,导致这些对象永远不会被释放,从而引发内存泄露。主要发生在使用std::shared_ptr时,因为它们…...

Stegdetect教程:如何用Stegdetect检测和破解JPG图像隐写信息
一、Stegdetect简介 Stegdetect 是一个开源工具,专门设计用于检测图像文件(JPG格式)中的隐写信息。Stegdetect 可以检测多种常见的隐写方法,比如 JSteg、JPHide 和 OutGuess 等。 二、使用Stegdetect检测图像隐写 官方描述&#…...

Co-Detr
参考:https://www.bilibili.com/video/BV1Sh4y1F7ur/?spm_id_from333.788&vd_source156234c72054035c149dcb072202e6be 之前的detr正样本数量少,匹配不平衡。 主要修改两个地方:encoder和decoder。 1.在encoder之后加入RPN,a…...

校园选课助手【1】-项目整体架构从此开始
项目背景 随着高校招生规模的不断扩大,学生选课需求日益增长。为提高选课效率,降低学生选课压力,本项目旨在开发一款校园选课助手软件。 项目目标:开发一款具有以下特点的校园选课助手软件: 易用性:界面简洁ÿ…...

椭圆曲线加法运算
1. 定义 椭圆曲线 (Elliptic Curve) 不是函数,而是一条平面曲线,其方程是定义如下: y 2 x 3 a x b y^2x^3axb y2x3axb 其中,判别式 Δ − 16 ( 4 a 3 27 b 2 ) ≠ 0 \Delta -16(4a^327b^2)\neq 0 Δ−16(4a327b2)0。判别…...

(STM32笔记)九、RCC时钟树与时钟 第一部分
我用的是正点的STM32F103来进行学习,板子和教程是野火的指南者。 之后的这个系列笔记开头未标明的话,用的也是这个板子和教程。 九、RCC时钟树与时钟 九、RCC时钟树与时钟1、时钟树HSE时钟HSI时钟锁相环时钟系统时钟HCLK时钟PCLK1时钟PCLK2时钟RTC时钟独…...
fastjson-流程分析
参考视频:fasfjson反序列化漏洞1-流程分析 分析版本 fastjson1.2.24 JDK 8u65 分析过程 新建Person类 public class Person {private String name;private int age;public Person() {System.out.println("constructor_0");}public Person(String na…...
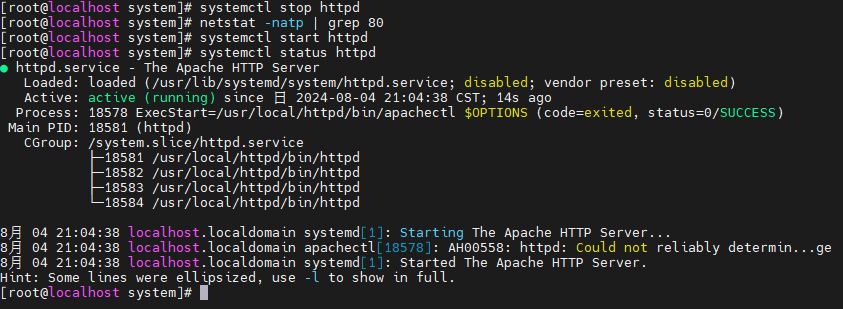
Linux 命令安装
系列文章目录 提示:仅用于个人学习,进行查漏补缺使用。 1.Linux介绍、目录结构、文件基本属性、Shell 2.Linux常用命令 3.Linux文件管理 4.Linux 命令安装 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助…...

清华和字节联合推出的视频理解大模型video-SALMONN(ICML 2024)
video-SALMONN: Speech-Enhanced Audio-Visual Large Language Models 论文信息 paper:https://arxiv.org/abs/2406.15704 code:https://github.com/bytedance/SALMONN/ AI也会「刷抖音」!清华领衔发布短视频全模态理解新模型 | ICML 2024 …...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
