代码随想录算法训练营第二天 | 209. 长度最小的子数组、59. 螺旋矩阵 II
目录
- 209. 长度最小的子数组
- 1、题目描述
- 2、思路
- 3、code
- 4、复杂度分析
- LC59 螺旋矩阵 II
- 1、题目描述
- 2、思路
- 3、code
- 4、复杂度分析
209. 长度最小的子数组
题目链接:209
1、题目描述
给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
2、思路
1️⃣ 暴力法,两个for循环嵌套,时间复杂度 O ( n 2 ) O(n^2) O(n2)
2️⃣ 题目基本是根据连续子序列的情况,不断调节子序列的起始和终止位置:滑动窗口
模板:
3、code
class Solution:def minSubArrayLen(self, target: int, nums: List[int]) -> int:# 找一个数组的满足条件的最短或者最长连续子数组:滑动窗口minlen = float('inf')start = 0sum_sub = 0for end in range(0,len(nums)):sum_sub += nums[end]while sum_sub >= target:minlen = min(minlen, end-start+1)sum_sub -= nums[start]start += 1if minlen <= len(nums):return minlenelse:return 0
4、复杂度分析
- 时间复杂度:
每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n) - 空间复杂度:没有创建数组 O ( 1 ) O(1) O(1)
LC59 螺旋矩阵 II
题目链接:59
1、题目描述
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix
示例 1:
2、思路
要控制每次循环的区间范围(循环不变量)
按照左闭右开的原则,来画一圈,大家看一下:

3、code
class Solution:def generateMatrix(self, n: int) -> List[List[int]]:# 首先先初始化一个全是0的nxn二维矩阵mat = [[0 for _ in range(n)] for _ in range(n)]# 定义每一圈的起始点坐标start_x = 0start_y = 0# 定义表示不同圈的每一条边的倒数第二个节点的偏移量# 比如第1圈是j = (n-1) - 1# 第2圈就是j = (n-1) - 2offset = 1# 定义要往矩阵中填入的数count = 1loop = n //2# 循环开始for time in range(0,loop):# 填充上行从左到右:横坐标不变且是start_x,纵坐标从start_y到(n - 1) - 1for j in range(start_y, n - offset):# 因为range“顾头不顾腚”所以可以少写一个-1mat[start_x][j] = countcount += 1# 填充右列从上到下:横坐标从start_x到(n-1)-offset,纵坐标不变且是上行最后一个元素的坐标加一(j = n - offset) # 此时到达了上行的倒数第二个元素(start_x,j = (n-1)-offset)# 那么右列的第一个元素就是(start_x,n - offset)for i in range(start_x, n - offset):mat[i][n - offset] = countcount += 1# 填充下行从右到左:横坐标不变是上列最后一个元素的横坐标加一(i = n - offset),纵坐标从上一次的j = n - offset 一直减到start_y + 1for j in range(n - offset, start_y, -1):mat[n - offset][j] = countcount += 1# 填充左列从下到上:横坐标从上一次的i = n - offset一只减到start_x + 1,纵坐标不变就是上一行最后一个元素的纵坐标减一(start_y)for i in range(n - offset, start_x, -1):mat[i][start_y] = countcount += 1# 更新起始点坐标start_x += 1start_y += 1offset += 1mid = n // 2if n%2 != 0:mat[mid][mid] = count return mat
4、复杂度分析
1️⃣ 时间复杂度: n / 2 ∗ 4 ∗ ( n − k ) = n 2 n/2 * 4 *(n-k) = n^2 n/2∗4∗(n−k)=n2
2️⃣ 空间复杂度:1
相关文章:

代码随想录算法训练营第二天 | 209. 长度最小的子数组、59. 螺旋矩阵 II
目录 209. 长度最小的子数组1、题目描述2、思路3、code4、复杂度分析 LC59 螺旋矩阵 II1、题目描述2、思路3、code4、复杂度分析 209. 长度最小的子数组 题目链接:209 1、题目描述 给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于…...
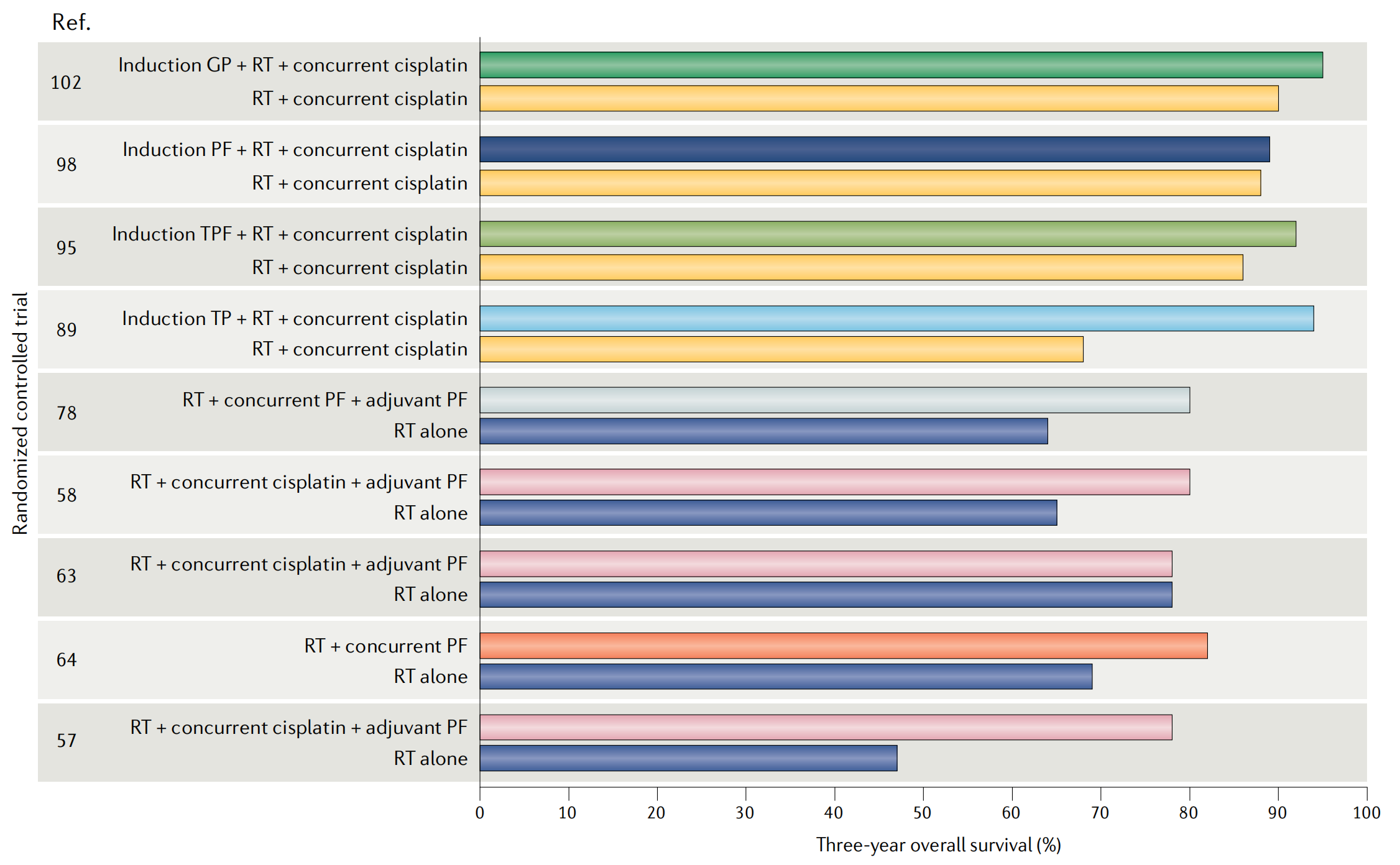
鼻咽癌综述
小罗碎碎念 本期推文主题:鼻咽癌综述 这篇文章提供了一个全面的综述,探讨了鼻咽癌(NPC)的关键研究进展,包括病理机制、治疗、筛查和生物标志物的发展。 文章首先强调了NPC在特定地理区域的流行情况,并讨论了…...

中国AI PC行业研究报告
核心摘要: 2020-2023年中国笔电出货量呈下降趋势,PC厂商亟需从产品形态、软硬技术、需求场景等角度寻求新的增长机会。而随着大模型、生成式AI技术的到来,其强大的数据处理、学习泛化与内容生成能力,高质效加速了各行各业人工智能…...

Mybatis实战:图书管理系统(笔记)
前言:如果在接口的声明方法中鼠标右键没有Test的单元测试。 你的鼠标光标问题:要在花括号范围内!!!! 数据库表是应⽤程序开发中的⼀个重要环节, 数据库表的设计往往会决定我们的应⽤需求是否能顺利实现, 甚…...

win11 amd64 python安装matplotlib、pytorch报错记录
win11 amd64 python matplotlib 安装报错记录 安装时 错误是 metadata-generation-failed 查看上面的具体报错原因,来自: Files\Python\Python3_10_11\Include: linker input file not found: No such file or director注意Python 的路径中最好不要有…...
)
Python写UI自动化--playwright(等待页面加载机制)
很多情况下,我们都需要等待页面加载到一定程度才能进行下一步操作,而这个度该怎么操作,这篇文章就来详细讲一讲 目录 expect_popup() wait_until参数 "load" commit: "domcontentloaded" "networkidle"…...
0804)
书籍将整数字符串转成整数值(5)0804
题目 给定一个字符串str,如果str符合日常书写的整数形式,并且属于32位整数的范围,返回str所代表的整数值,否则返回0。 举例 str“123” 返回 123 str“023” 因为023 不符合日常的书写习惯,所以返回0 str“A13” …...

【2024年华数杯C题老外游中国】(完整题解+代码+完整参考论文)
请问 352 个城市中所有 35200 个景点评分的最高分(Best Score,简称 BS)是多少?全国有多少个景点获评了这个最高评分(BS)?获评了这个最高评分(BS)景点最多的城市有哪些&am…...

全球氢化双酚A (HBPA)市场规划预测:2030年市场规模将接近1330亿元,未来六年CAGR为2.7%
一、引言 随着全球化工行业的持续发展,氢化双酚A (HBPA)作为重要的化工原料,其市场重要性日益凸显。本文旨在探索HBPA行业的发展趋势、潜在商机及其未来展望。 二、市场趋势 全球HBPA市场的增长主要受全球化工行业增加、消费者对高性能化工产品要求提高…...

【C++】异常处理:深度解析与实战精髓,不容错过的编程秘籍
🌈 个人主页:Zfox_ 🔥 系列专栏:C从入门到精通 目录 🚀 前言:C语言传统的处理错误的方式 一: 🔥 C异常概念二: 🔥 异常的使用 2.1 📖 异常的抛出和…...

智能指针的循环引用 是什么 怎么引起的
智能指针的循环引用 是什么 怎么引起的 智能指针的循环引用(Circular Reference)是指两个或多个对象之间的共享指针相互引用,导致这些对象永远不会被释放,从而引发内存泄露。主要发生在使用std::shared_ptr时,因为它们…...

Stegdetect教程:如何用Stegdetect检测和破解JPG图像隐写信息
一、Stegdetect简介 Stegdetect 是一个开源工具,专门设计用于检测图像文件(JPG格式)中的隐写信息。Stegdetect 可以检测多种常见的隐写方法,比如 JSteg、JPHide 和 OutGuess 等。 二、使用Stegdetect检测图像隐写 官方描述&#…...

Co-Detr
参考:https://www.bilibili.com/video/BV1Sh4y1F7ur/?spm_id_from333.788&vd_source156234c72054035c149dcb072202e6be 之前的detr正样本数量少,匹配不平衡。 主要修改两个地方:encoder和decoder。 1.在encoder之后加入RPN,a…...

校园选课助手【1】-项目整体架构从此开始
项目背景 随着高校招生规模的不断扩大,学生选课需求日益增长。为提高选课效率,降低学生选课压力,本项目旨在开发一款校园选课助手软件。 项目目标:开发一款具有以下特点的校园选课助手软件: 易用性:界面简洁ÿ…...

椭圆曲线加法运算
1. 定义 椭圆曲线 (Elliptic Curve) 不是函数,而是一条平面曲线,其方程是定义如下: y 2 x 3 a x b y^2x^3axb y2x3axb 其中,判别式 Δ − 16 ( 4 a 3 27 b 2 ) ≠ 0 \Delta -16(4a^327b^2)\neq 0 Δ−16(4a327b2)0。判别…...

(STM32笔记)九、RCC时钟树与时钟 第一部分
我用的是正点的STM32F103来进行学习,板子和教程是野火的指南者。 之后的这个系列笔记开头未标明的话,用的也是这个板子和教程。 九、RCC时钟树与时钟 九、RCC时钟树与时钟1、时钟树HSE时钟HSI时钟锁相环时钟系统时钟HCLK时钟PCLK1时钟PCLK2时钟RTC时钟独…...
fastjson-流程分析
参考视频:fasfjson反序列化漏洞1-流程分析 分析版本 fastjson1.2.24 JDK 8u65 分析过程 新建Person类 public class Person {private String name;private int age;public Person() {System.out.println("constructor_0");}public Person(String na…...
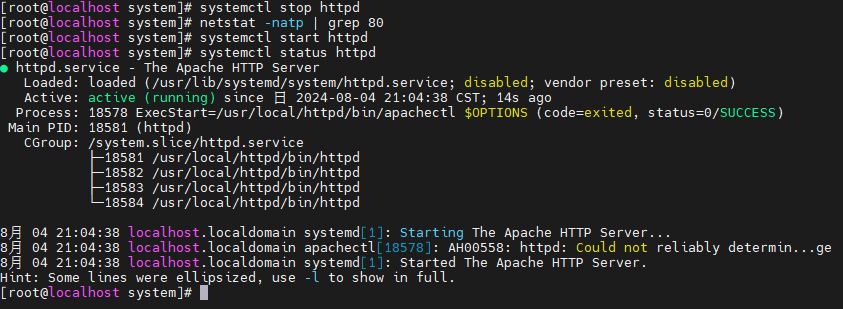
Linux 命令安装
系列文章目录 提示:仅用于个人学习,进行查漏补缺使用。 1.Linux介绍、目录结构、文件基本属性、Shell 2.Linux常用命令 3.Linux文件管理 4.Linux 命令安装 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助…...

清华和字节联合推出的视频理解大模型video-SALMONN(ICML 2024)
video-SALMONN: Speech-Enhanced Audio-Visual Large Language Models 论文信息 paper:https://arxiv.org/abs/2406.15704 code:https://github.com/bytedance/SALMONN/ AI也会「刷抖音」!清华领衔发布短视频全模态理解新模型 | ICML 2024 …...

从数据爬取到可视化展示:Flask框架与ECharts深度解析
目录 🔹 Flask框架源码解析 Flask应用初始化路由与视图函数请求与响应中间件 🔹 ECharts可视化精讲 ECharts安装与配置基本图表类型图表样式与交互高级图表配置与数据动态更新实战:结合Flask与ECharts展示爬取数据 Flask框架源码解析 &…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

