Lesson 8.1 决策树的核心思想与建模流程
文章目录
- 一、借助逻辑回归构建决策树
- 1. 决策树实例
- 2. 决策树知识补充
- 2.1 决策树简单构建
- 2.2 决策树的分类过程
- 2.3 决策树模型本质
- 2.4 决策树的树生长过程
- 2.5 树模型的基本结构
- 二、决策树的分类与流派
- 1. ID3(Iterative Dichotomiser 3) 、C4.5、C5.0 决策树
- 2. CART 决策树
- 3. CHAID 树
- 与此前的聚类算法类似,树模型也同样不是一个模型,而是一类模型的概称。
- 树模型不仅运算效率高、模型判别能力强、而且原理简单过程清晰、可解释性强,是机器学习领域内为数不多的白箱模型。
- 并且就树模型本身的功能来说,除了能够同时进行分类和回归预测外,还能够产出包括特征重要性、连续变量分箱指标等重要附加结论,而在集成学习中,最为常用的基础分类器也正是树模型。
- 正是这些优势,使得树模型成为目前机器学习领域最为重要的模型之一。
一、借助逻辑回归构建决策树
1. 决策树实例
- 那到底什么是树模型?接下来我们简单介绍树模型建模的基本思想 。
- 尽管树模型作为经典模型,发展至今已是算法数量众多、流派众多,但大多数树模型的基本思想其实是相通的,我们可以用一句话来解释树模型的模型形态和建模目标,那就是:挖掘有效分类规则并以树状形式呈现。
- 接下来我们就以一个简单实例进行说明,我们借助此前所学的基本建模知识,尝试复现决策树的基本分类思想。
- 在最开始,我们先导入常用的模块。
# 科学计算模块
import numpy as np
import pandas as pd
# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt
# 自定义模块
from ML_basic_function import *
# Scikit-Learn相关模块
# 评估器类
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import GridSearchCV
# 实用函数
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 数据准备
from sklearn.datasets import load_iris
- 在 Lesson 6.5 节中,我们曾围绕鸢尾花数据集构建了多分类逻辑回归模型并且采用网格搜索对其进行最优超参数搜索,其基本过程如下:
# 数据准备
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=24)# 模型训练
# 实例化模型
clf = LogisticRegression(max_iter=int(1e6), solver='saga')
# 构建参数空间
param_grid_simple = {'penalty': ['l1', 'l2'], 'C': [1, 0.5, 0.1, 0.05, 0.01]}
# 构建网格搜索评估器
search = GridSearchCV(estimator=clf, param_grid=param_grid_simple)
# 模型训练
search.fit(X_train, y_train)
#GridSearchCV(estimator=LogisticRegression(max_iter=1000000, solver='saga'),
# param_grid={'C': [1, 0.5, 0.1, 0.05, 0.01], 'penalty': ['l1', 'l2']})search.best_params_
#{'C': 1, 'penalty': 'l1'}search.best_estimator_.coef_
#array([[ 0. , 0. , -3.47337669, 0. ],
# [ 0. , 0. , 0. , 0. ],
# [-0.55511761, -0.34237661, 3.03227709, 4.12148646]])search.best_estimator_.intercept_
#array([ 11.85884734, 2.65291107, -14.51175841])
- 我们发现,在参数组取值为 {‘C’: 1, ‘penalty’: ‘l1’} 的情况下,三个逻辑回归方程中,第一个方程只包含一个系数,也就是说明第一个方程实际上只用到了原数据集的一个特征,第二个方程自变量系数均为 0、基本属于无用方程,而只有第三个方程自变量系数都不是 0、看起来比较正常。
- 我们知道,对于多分类问题,逻辑回归所构建的模型方程实际上是每个方程对应预测一个类别,而由于总共只有三个类别,因此是允许存在一个类别的预测方程失效的,只要剩下的两个类别能够各自完成对应类别的预测,则剩下的样本就属于第三类。
- 此处我们需要重点关注的是第一个方程,该方程只有一个非零系数,其背后含义是模型只借助特征矩阵中的第三个特征,就很好的将第一类鸢尾花和其他鸢尾花区分开了。
- 我们进一步观察数据和第三个特征对于第一个类别的分类结果:
iris = load_iris(as_frame=True)
iris.data
# sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
#0 5.1 3.5 1.4 0.2
#1 4.9 3.0 1.4 0.2
#2 4.7 3.2 1.3 0.2
#3 4.6 3.1 1.5 0.2
#4 5.0 3.6 1.4 0.2
#... ... ... ... ...
#145 6.7 3.0 5.2 2.3
#146 6.3 2.5 5.0 1.9
#147 6.5 3.0 5.2 2.0
#148 6.2 3.4 5.4 2.3
#149 5.9 3.0 5.1 1.8
#150 rows × 4 columnst = np.array(iris.target)
t[50:]
#array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
# 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
# 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])# 将2、3类划归为一类
t[50:] = 1
t
#array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
# 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
# 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
# 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])# 此处提取第3、4个特征放置二维空间进行观察,用第三个特征和其他特征组合也是类似
d = np.array(iris.data.iloc[:, 2: 4])plt.scatter(d[:, 0], d[:, 1], c=t)
plt.plot(np.array([2.5]*25), np.arange(0, 2.5, 0.1), 'r--')
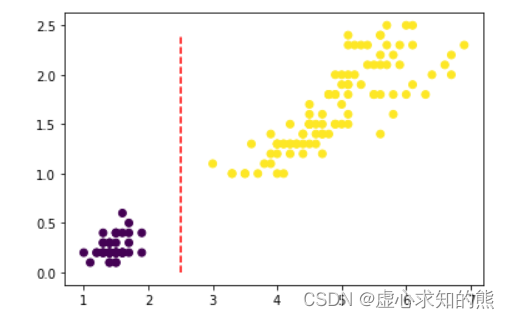
- 我们发现,确实可以通过第三个特征(横坐标)很好的区分第一类(紫色点簇)和其他两类(黄色点簇),也就是说,从分类结果来看,我们能够简单通过一个分类规则来区分第一类鸢尾花和其他两类.
- 例如从上图可以看出,我们可以以 petal length (cm) <= 2.5 作为分类条件,当分类条件满足时,鸢尾花属于第一类,否则就属于第二、三类。至此我们集完成了对上述数据集的初步分类,基本分类情况可以通过下图来进行表示:
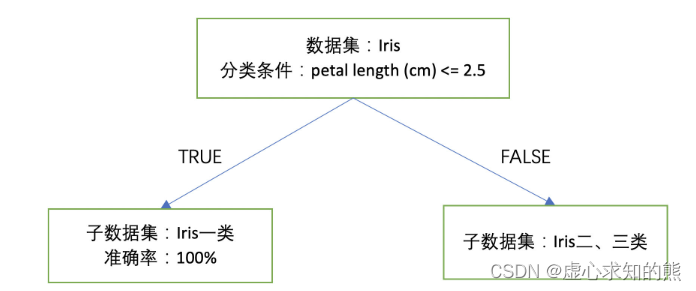
- 当然围绕上述未分类的二、三类鸢尾花数据,我们能否进一步找到类似刚才的分类规则对其进行有效分类呢?
- 当然此处由于我们希望分类规则能够尽可能简洁,我们力求找出根据某一个特征的取值划分就能对数据集进行有效分类的方法,这时我们可以考虑先利用逻辑回归的 l1l1l1 正则化挑选出对二、三类分类最有分类效力的特征(也就是最重要的特征)。
- 然后根据只有一个特征系数不为 0 的带 l1l1l1 正则化的逻辑回归建模结果、找到决策边界,而该决策边界就是依据该单独特征划分 Iris 二、三类子数据的最佳方法。我们可以通过下述代码实现:
# 提取待分类的子数据集
X = np.array(iris.data)[t == 1]
y = np.array(iris.target)[t == 1]
- 接下来,我们构建一个包含 l1l1l1 正则化的逻辑回归模型,并通过不断调整 C 的取值、通过观察参数系数变化情况来挑选最重要的特征:
C_l = np.linspace(1, 0.1, 100)coef_l = []
for C in C_l:clf = LogisticRegression(penalty='l1', C=C, max_iter=int(1e6), solver='saga').fit(X, y)coef_l.append(clf.coef_.flatten())ax = plt.gca()
ax.plot(C_l, coef_l)
ax.set_xlim(ax.get_xlim()[::-1])
plt.xlabel('C')
plt.ylabel('weights')
Text(0, 0.5, 'weights')
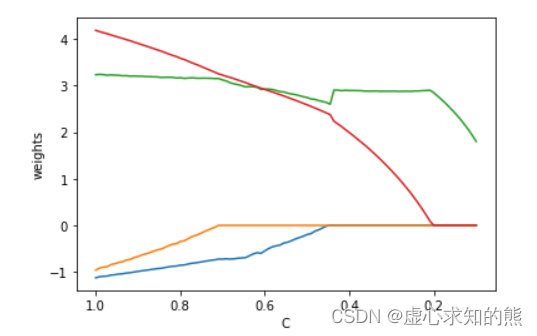
coef_l
- 不难看出,在对鸢尾花数据集的二、三分类的子数据集进行分类时,仍然还是第三个特征会相对重要,因此我们根据上述结果,构建一个正则化项为 l1l1l1、C 取值为 0.2 的逻辑回归模型进行训练,此时由于其他三个特征的参数都被归零,因此该模型训练过程实际上就相当于带入第三个特征进行建模:
clf = LogisticRegression(penalty='l1', C=0.2, max_iter=int(1e6), solver='saga').fit(X, y)clf.coef_, clf.intercept_
#(array([[0. , 0. , 2.84518611, 0. ]]),
# array([-13.88186328]))clf.score(X, y)
#0.93
- 此时模型准确率为 93%,同样,如果构建一个只包含第三、四个特征的特征空间,此时上述逻辑回归建模结果的决策边界为 x=b,其中 b 的取值如下:
b = 13.88186328 / 2.84518611
b
#4.87907038179657
- 我们可以通过可视化的方法观察此时特征空间中样本分布情况,以及 x=b 的决策边界的分类效果:
plt.plot(X[:, 2][y==1], X[:, 3][y==1], 'ro')
plt.plot(X[:, 2][y==2], X[:, 3][y==2], 'bo')
plt.plot(np.array([b]*20), np.arange(0.5, 2.5, 0.1), 'r--')
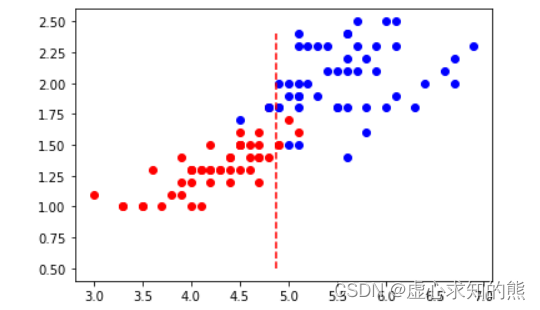
- 当然,我们也可以简单验算下 x=b 的决策边界是否是模型真实的分类边界:
y_pred = clf.predict(X)plt.scatter(X[:, 2], X[:, 3], c=y_pred)
plt.plot(np.array([b]*20), np.arange(0.5, 2.5, 0.1), 'r--')
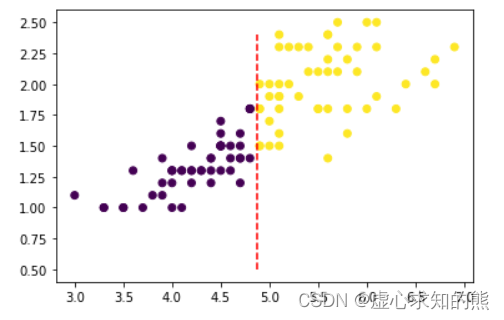
- 注意,在确定第一个分类条件时我们没有直接根据逻辑回归的线性方程计算决策边界的主要原因是彼时逻辑回归方程是在 mvm 分类规则下的三个分类方程,其中每个方程其实都会一定程度上受到其他方程影响,导致决策边界无法直接通过方程系数进行计算。
- 尽管 x=b 分类边界的准确率不足 100%,但其仍然不失为一个不错的分类规则,即分类条件为 petal length (cm) <= 4.879,当分类条件满足时,鸢尾花属于第二类、不满足时鸢尾花属于第三类。
- 根据此分类条件进行的分类准确率为 93%。我们可以将围绕鸢尾花子数据集进行二、三类的分类过程进行如下方式表示:
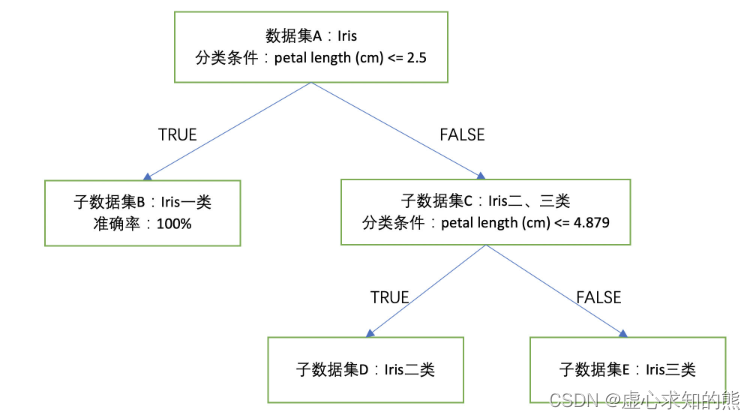
- 至此,我们就根据两个简单的分类规则,对鸢尾花数据集进行了有效划分,此时整体准确率为:
1-(y != y_pred).sum() / 150
#0.9533333333333334
2. 决策树知识补充
2.1 决策树简单构建
- 而上述整个过程,我们是通过带正则化项的逻辑回归模型挖掘出的两个分类规则,并且这两个分类规则呈现递进的关系,也就是一个分类规则是在另一个分类规则的分类结果下继续进行分类,最终这两个分类规则和对应划分出来的数据集呈现出树状,而带有不同层次分类规则的模型,其实就是决策树模型,也就是说通过上面一系列的操作,我们就已经成功构建了一个决策树模型。
2.2 决策树的分类过程
- 对于上述已经构建好的一个决策树来说,当对新数据进行判别时,任意进来一条数据我们都可以自上而下进行分类,先根据 petal length (cm) <= 2.5 判断是否属于第一类,如果不满足条件则不属于第一类,此时进一步考虑 petal length (cm) <= 4.879 是否满足条件,并据此判断是属于第二类还是第三类。
- 当然,目前主流的决策树并不是依据逻辑回归来寻找分类规则,但上述构建决策树模型的一般过程和核心思想和目前主流的决策树模型并无二致,因此我们可以围绕上述过程进行进一步总结。
2.3 决策树模型本质
- 当决策树模型构建好了之后,实际上一个决策树就是一系列分类规则的叠加,换而言之,决策树模型的构建从本质上来看就是在挖掘有效的分类规则,然后以树的形式来进行呈现。
2.4 决策树的树生长过程
- 在整个树的构建过程中,我们实际上是分层来对数据集进行划分的,每当定下一个分类规则后,我们就可以根据是否满足分类规则来对数据集进行划分,而后续的分类规则的挖掘则进一步根据上一层划分出来的子数据集的情况来定,逐层划分数据集、逐数据集寻找分类规则再划分数据集,实际上就就是树模型的生长过程。
- 这个过程实际上也是一个迭代计算过程(上一层的数据集决定有效规律的挖掘、而有效规律的挖掘)。而停止生长的条件,我们也可以根据继续迭代对结果没有显著影响这个一般思路来构建。
2.5 树模型的基本结构
- 当然,在已经构建了决策树之后,我们也能够对一个树模型的内部结构来进行说明。
- 对上述决策树来说,我们可以将其看成是点(数据集)和线构成的一个图结构(准确来说应该是一种有向无环图),而对于任何一个图结构,我们都能够通过点和线来构建对其的基本认知。
- 对于决策树来说,我们主要将借助边的方向来定义不同类型点,首先我们知道如果一条边从 A 点引向 B 点,则我们这条边对于 A 点来说是出边、对于 B 点来说是入边,A 节点是 B 节点的父节点,据此我们可以将决策树中所有的点进行如下类别划分:
- (1) 节点(root node):没有入边,但有零条或者多条出边的点;
- (2) 内部点(internal node):只有一条入边并且有两条或多条出边的点;
- (3) 叶节点(leaf node):只有入边但没有出边的点;
- 因此,我们知道在一次次划分数据集的过程中,原始的完整数据集对应着决策树的根节点,而根结点划分出的子数据集就构成了决策树中的内部节点,同时迭代停止的时候所对应的数据集,其实就是决策树中的叶节点。
- 并且在上述二叉树(每一层只有两个分支)中,一个父节点对应两个子节点。并且根据上述决策树的建模过程不难理解,其实每个数据集都是由一系列分类规则最终划分出来的,我们也可以理解成每个节点其实都对应着一系列分类规则,例如上述 E 节点实际上就是 petal length (cm) <= 2.5 和 petal length (cm) <= 4.879 同时为 False 时划分出来的数据集。
二、决策树的分类与流派
- 正如此前所说,树模型并不是一个模型,而是一类模型。需要知道的是,尽管树模型的核心思想都是源于一种名为贪心算法的局部最优求解算法,但时至今日,树模型已经有数十种之多,并且划分为多个流派。目前主流的机器学习算法类别可划分如下:
1. ID3(Iterative Dichotomiser 3) 、C4.5、C5.0 决策树
- ID3(Iterative Dichotomiser 3) 、C4.5、C5.0 决策树是最为经典的决策树算法、同时也是真正将树模型发扬光大的一派算法。
- 最早的 ID3 决策树由 Ross Quinlan 在 1975 年(博士毕业论文中)提出,至此也奠定了现在决策树算法的基本框架——确定分类规则判别指标、寻找能够最快速降低信息熵的方式进行数据集划分(分类规则提取),不断迭代直至收敛。
- 而 C4.5 则是 ID3 的后继者,C4.5 在 ID3 的基础上补充了一系列基础概念、同时也优化了决策树的算法流程,一方面使得现在的树模型能够处理连续变量(此前的 ID3 只能处理分类变量),同时也能够一定程度提高树模型的生长速度,而 C4.5 也是目前最为通用的决策树模型的一般框架,后续尽管有其他的决策树模型诞生,但大都是在 C4.5 的基本流程上进行略微调整或者指标修改。
- 此外,由于 C4.5 开源时间较早,这也使得在过去的很长一段时间内,C4.5 都是最通用的决策树算法。当然在此后,Ross Quinlan 又公布了 C5.0 算法,进一步优化了运行效率和预测流程,通过一系列数据结构的调整使得其能够更加高效的利用内存、并提高执行速度。
2. CART 决策树
- CART 全称为 Classification and Regression Trees,即分类与回归决策树,同时也被称为 C&RT 算法,在 1984 年由 Breiman、Friedman、Olshen 和 Stone 四人共同提出。
- CART 树和 C4.5 决策树的构造过程非常类似,但拓展了回归类问题的计算流程(此前 C4.5 只能解决分类问题),并且允许采用更丰富的评估指标来指导建模流程,并且,最关键的是,CART 算法其实是一个非常典型的机器学习算法,在早期 CART 树的训练过程中,就是通过划分训练集和验证集(或者测试集)来验证模型结果、并进一步据此来调整模型结构。
- 当然,除此以外,CART 树还能够用一套流程同时处理离散变量和连续变量、能够同时处理分类问题和回归问题。
- 此处我们也可以参考 sklearn 中对于 ID3、C4.5 和 CART 树的对比描述:

- 需要注意的是,sklearn 中也并非实现的是完全的 CART 树,通过相关评估器参数的调整,sklearn 中也能实现 CART 树的建模流程 + C4.5 的决策树生长指标这种混合模型。
3. CHAID 树
- CHAID 是 Chi-square automatic interaction detection 的简称,由 Kass 在 1975 年提出,如果说 CART 树是一个典型的机器学习算法,那么 CHAID 树就是一个典型的统计学算法。
- 从该算法的名字就能看出,整个决策树其实是基于卡方检验(Chi-square)的结果来构建的,并且整个决策树的建模流程(树的生长过程)及控制过拟合的方法(剪枝过程)都和 C4.5、CART 有根本性的区别,例如 CART 都只能构建二叉树,而 CHAID 可以构建多分枝的树(注:C4.5 也可以构建多分枝的树)。
- 例如 C4.5 和 CART 的剪枝都是自下而上(Bottom-up)进行剪枝,也被称为修剪法(Pruning Technique),而 CHAID 树则是自上而下(Top-Down)进行剪枝,也被称为盆栽法(Bonsai Technique)。
相关文章:

Lesson 8.1 决策树的核心思想与建模流程
文章目录一、借助逻辑回归构建决策树1. 决策树实例2. 决策树知识补充2.1 决策树简单构建2.2 决策树的分类过程2.3 决策树模型本质2.4 决策树的树生长过程2.5 树模型的基本结构二、决策树的分类与流派1. ID3(Iterative Dichotomiser 3) 、C4.5、C5.0 决策树2. CART 决策树3. CHA…...

【算法】FIFO先来先淘汰算法分析和编码实战
背景 在设计一个系统的时候,由于数据库的读取速度远小于内存的读取速度 为加快读取速度,将一部分数据放到内存中称为缓存,但内存容量是有限的,当要缓存的数据超出容量,就需要删除部分数据 这时候需要设计一种淘汰机制…...
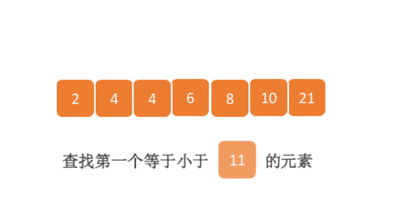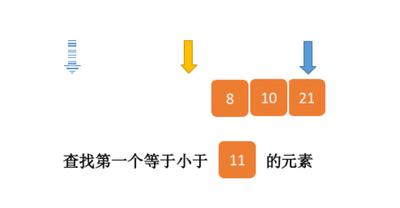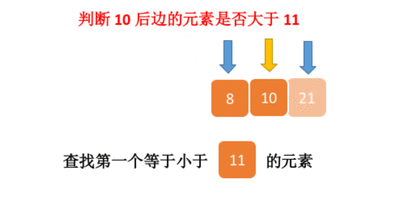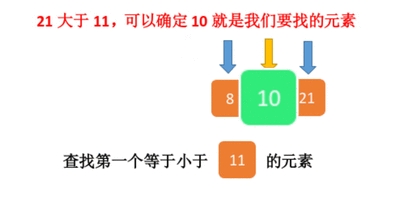
二分查找——我欲修仙(功法篇)
个人主页:【😊个人主页】 系列专栏:【❤️我欲修仙】 学习名言:临渊羡鱼,不如退而结网——《汉书董仲舒传》 系列文章目录 第一章 ❤️ 二分查找 文章目录系列文章目录前言🚗🚗🚗二分查找&…...

Python 多线程
文章目录一、简介1.1 多线程的特性1.2 GIL二、线程1.2 单线程1.3 多线程三、线程池3.1 pool.submit3.2 pool.map四、Lock(线程锁)4.1 无锁导致的线程资源异常4.2 有锁五、Event(事件)5.1 简介5.2 示例六、Queue(队列&a…...
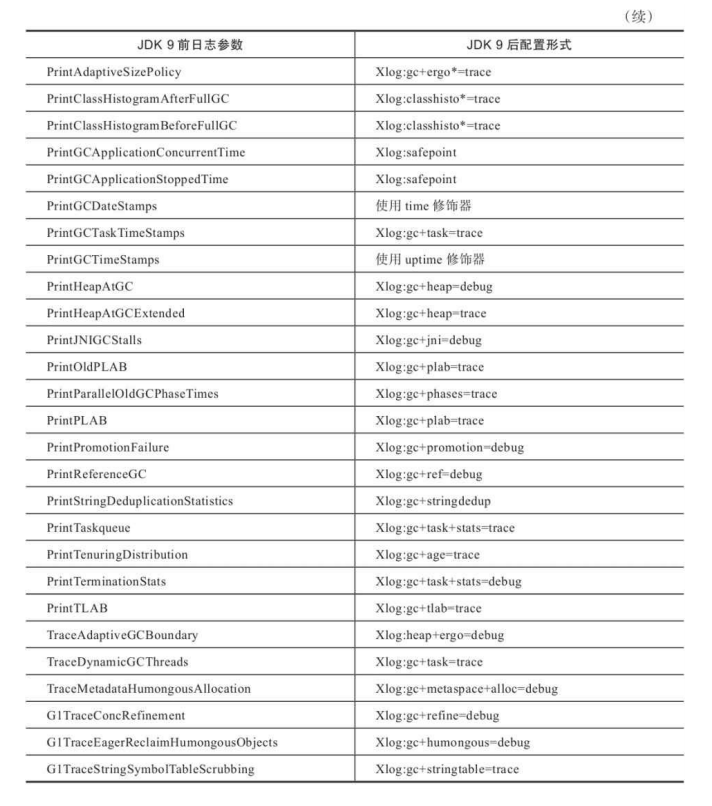
JVM笔记(九)选择合适的垃圾收集器
Epsilon收集器Epsilon收集器由RedHat公司在JEP 318中提出,在此提案里Epsilon被形容成一个无操作的收集器(A No-Op Garbage Collector),而事实上只要Java虚拟机能够工作,垃圾收集器便不可能是真正“无操作”的。原因是“…...

二维图像处理到三维点云处理
一、Opencv和PCL 下面是opencv和pcl的特点、区别和联系的详细对比表格。 特点/区别/联系OpenCVPCL英文全称Open Source Computer Vision LibraryPoint Cloud Library语言C、Python、JavaC功能图像处理(图像处理和分析、特征提取和描述、图像识别和分类、目标检测和跟踪等)、计…...

leetcode 删除有序数组中的重复项
题目 给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。 由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一…...

JVM学习.03 类加载机制
1、前言从事Java开发工作的都知道,Java程序提交到JVM运行时,需要编译成Class文件,才能被JVM加载运行。那么这些Class文件进入到虚拟机后会发生什么?以及Class是如何被加载的?这些都是本文要讲解的部分。2、类加载时机所…...
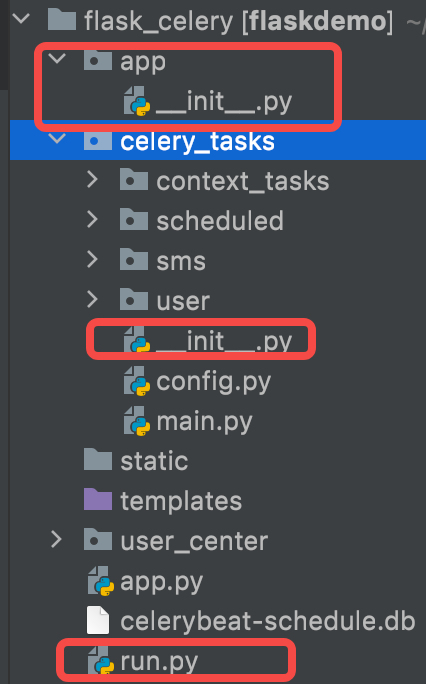
Celery使用:优秀的python异步任务框架
目录Celery 简介介绍安装基本使用Flask使用Celery异步任务定时任务Celery使用Flask上下文进阶使用参考停止Worker后台运行Celery 简介 介绍 Celery 是一个简单、灵活且可靠的,处理大量消息的分布式系统,并且提供维护这样一个系统的必需工具。 它是一个…...
第十四届蓝桥杯三月真题刷题训练——第 19 天
第 1 题:灌溉_BFS板子题 题目描述 小蓝负责花园的灌溉工作。 花园可以看成一个 n 行 m 列的方格图形。中间有一部分位置上安装有出水管。 小蓝可以控制一个按钮同时打开所有的出水管,打开时,有出水管的位置可以被认为已经灌溉好。 每经过一分…...

类和对象 - 下
本文已收录至《C语言》专栏! 作者:ARMCSKGT 目录 前言 正文 初始化列表 成员变量的定义与初始化 初始化列表的使用 变量定义顺序 explicit关键字 隐式类型转换 自定义类型隐式转换 explicit 限制转换 关于static static声明类成员 友元 友…...

【云原生】Linux基础IO(文件理解与操作)
✨个人主页: Yohifo 🎉所属专栏: Linux学习之旅 🎊每篇一句: 图片来源 🎃操作环境: CentOS 7.6 阿里云远程服务器 Great minds discuss ideas. Average minds discuss events. Small minds disc…...

CentOS 7 安装 mysql 8.0 客户端
只想安装 mysql-client 8.0 , 结果发现直接 yum install mysql mysql-client 安装的版本是 mysql Ver 15.1 Distrib 5.5.68-MariaDB ,这个版本太低,连接其他服务器上的 mysql 8.0 时总是失败,因为 mysql 8.0 加密方式改变了&#…...

Ubuntu下载、配置、安装和编译opencv
1 安装相关依赖安装opencv前,需要先准备好编译器、相关依赖sudo apt-get install gcc g cmake vim sudo apt-get install build-essential libgtk2.0-dev libavcodec-dev libavformat-dev libjpeg-dev libswscale-dev libtiff5-dev sudo apt-get install libgtk2.0-…...

第七讲 贪心
文章目录股票买卖 II货仓选址(贪心:排序中位数)糖果传递(❗贪心:中位数)雷达设备(贪心排序)付账问题(平均值排序❓)乘积最大(排序/双指针)后缀表达…...

数字藏品的未来及发展趋势
随着互联网的普及以及数字文化的日益发展,数字藏品作为一种全新的收藏方式正在逐步兴起。数字藏品可以是数字版权、数字艺术品、数字音乐以及数字视频等形式,这些藏品通过数字化技术保存下来,并在互联网上进行传播和交易。数字藏品的发展趋势…...

值得记忆的STL常用算法,分分钟摆脱容器调用的困境,以vector为例,其余容器写法类似
STL常用算法 概述: 算法主要是由头文件<algorithm> <functional> <numeric>组成 <algorithm>是所有STL头文件中最大的一个,范围涉及到比较、交换、查找、遍历操作、复制、修改等等 <nuneric>体积很小,只包括…...
java如何手动导jar包
今天用IDEA,需要导入一个Jar包,因为以前都是用eclipse的,所以对这个idea还不怎么上手,连打个Jar包都是谷歌了一下。 但是发现网上谷歌到的做法一般都是去File –> Project Structure中去设置,有没有如同eclipse一样…...

怎么防止SQL注入?
首先SQL注入是一种常见的安全漏洞,黑客可以通过注入恶意代码来攻击数据库和应用程序。以下是一些防止SQL注入的基本措施: 数据库操作层面 使用参数化查询:参数化查询可以防止SQL注入,因为参数化查询会对用户输入的数据进行过滤和…...
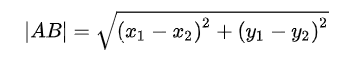
【千题案例】TypeScript获取两点之间的距离 | 中点 | 补点 | 向量 | 角度
我们在编写一些瞄准、绘制、擦除等功能函数时,经常会遇到计算两点之间的一些参数,那本篇文章就来讲一下两点之间的一系列参数计算。 目录 1️⃣ 两点之间的距离 ①实现原理 ②代码实现及结果 2️⃣两点之间的中点 ①实现原理 ②代码实现及结果 3…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
