力扣 3152. 特殊数字Ⅱ
题目描述

queries二维数组是nums数组待判断的索引区间(左闭右闭)。需要判断每个索引区间中的nums相邻元素奇偶性是否不同,如果都不同则该索引区间的搜索结果为True,否则为False。
暴力推演:也是我最开始的思路
遍历queries的索引区间,在每一个区间内再遍历相应的nums元素判断奇偶性是否不同。
那么,如何判断相邻元素的奇偶性不同呢?我想到的是:“奇数+偶数=奇数”而“奇数+奇数=偶数”、“偶数+偶数=偶数”,即判断相邻元素之和是否为奇数。
该思路代码如下:
class Solution:def isArraySpecial(self, nums: List[int], queries: List[List[int]]) -> List[bool]:# 相邻数字奇偶性不同:和为奇数。# 暴力搜索:遍历数组的每一个查询索引区间,依次判断。# 时间复杂度:O(M*N),其中M为queries的长度,N为nums的长度。answer = []for index_range in queries:result = True # 首先假设区间符合要求for i in range(index_range[0], index_range[1]): if (nums[i] + nums[i + 1]) % 2 == 0: # 检查和是否为偶数result = False # 找到一对不符合要求的相邻数字break # 找到后立即停止循环answer.append(result)return answer

这个思路时间复杂度过高。该如何优化呢?
我们发现这个思路再遍历queries每个区间时都要在nums中进行从头到尾的遍历,这一部分是不是可以优化呢?
比如可以先遍历nums中所有的元素,判断相邻元素奇偶性差异并在相应的位置做好标记,如果该位置与前一个元素的奇偶性不同,则该位置的标记与前一个位置的标记保持一致,否则+1,这样的话每次只需要判断区间首位位置的标记是否相同即可(时间复杂度即可变为O(M+N),如果相同则说明该区间所有的相邻元素奇偶性都不同,输出True,否则输出False。
看了题解,原来这个标记的思路其实可以用前缀和(之前很少用到,练练)来实现,而且判断两个元素奇偶性差异可以直接用位运算(也很少用到,正好练练)。
前缀和
前缀和是什么呢?
前缀和是一种在数组或序列中计算元素累积和的方法。具体来说,对于一个数组或序列中的元素,前缀和是指从第一个元素到当前元素(包括当前元素)的所有元素的和。
位运算是什么?
位运算是一种直接对整数的二进制位进行操作的运算方式。在计算机科学中,位运算是一种非常基础且高效的运算方式,它在底层硬件和编程语言中广泛使用。位运算主要包括以下几种类型:
1、AND(与)运算:符号为 &。两个位相与,只有两个位都是1时结果才是1,否则是0。
2、OR(或)运算:符号为 |。两个位相或,只要有一个位是1结果就是1,否则是0。
3、XOR(异或)运算:符号为 ^。两个位相异或,相同则结果为0,不同则结果为1。
4、NOT(非)运算:符号为 ~。对一个位取反,1变成0,0变成1。
5、左移(Left Shift)运算:符号为 <<。将一个数的所有位向左移动指定的位数,左边超出的位被丢弃,右边空出的位补0。
6、右移(Right Shift)运算:符号为 >>。将一个数的所有位向右移动指定的位数,右边超出的位被丢弃,左边空出的位补原数的符号位(算术右移)或补0(逻辑右移)。
位运算如何判断两个元素奇偶性差异?
对照上面的位运算类型,用异或!!
nums[i-1] ^ nums[i] == 1即为相邻元素奇偶性不同。
该思路代码如下:
class Solution:def isArraySpecial(self, nums: List[int], queries: List[List[int]]) -> List[bool]:# 前缀和:在数组或序列中计算元素累积和的方法,具体来说是指从第一个元素到当前元素(包括当前元素)的所有元素的和。# 快速计算某个范围内的元素总和的场景,可以帮助简化问题,提高算法效率。# 时间复杂度:O(M+N)n = len(nums)sum_array = [0] * nfor i in range(1, n):sum_array[i] = sum_array[i-1]if ((nums[i-1] ^ nums[i]) & 1) == 0: # 位运算判断,如果奇偶性相同条件则为真sum_array[i] += 1m = len(queries)answer = [False] * mfor i in range(m):index_range = queries[i]if sum_array[index_range[0]] == sum_array[index_range[1]]: #若区间两端的标记一致,则说明区间内的相邻元素均满足奇偶性不同的条件。answer[i] = Truereturn answer我试了试把位运算判断的条件改成:
if nums[i-1] ^ nums[i] == 0:
测试用例报错:

我觉得这两句效果一样,但输出结果就是不一样,也不知道为啥。。。留待后续!!
后续
用位运算判断两数的奇偶性差异:看二进制最后一位是否相同。而 nums[i-1] ^ nums[i] 会比较每一位是否相同,所以要 (nums[i-1] ^ nums[i]) & 1 ,因为只关注异或运算的最低位结果。
参考题解: 【预处理】前缀和 & 动态规划(详细思路+推导)
相关文章:

力扣 3152. 特殊数字Ⅱ
题目描述 queries二维数组是nums数组待判断的索引区间(左闭右闭)。需要判断每个索引区间中的nums相邻元素奇偶性是否不同,如果都不同则该索引区间的搜索结果为True,否则为False。 暴力推演:也是我最开始的思路 遍历q…...

识别和缓解软件安全威胁的最佳工具
软件安全威胁会给企业带来重大损失,从经济损失到声誉受损。 企业必须主动识别和缓解这些威胁,防止它们造成危害。 幸运的是,有许多工具可以帮助企业识别和缓解软件安全威胁。 在本博客中,我们将探讨识别和缓解软件安全威胁的顶…...

Linux下的压缩与解压:掌握核心命令行工具
目录 一.前言 二.压缩文件概述 三.tar:Linux 的通用归档工具 常用 tar 命令 四.gzip:强大的压缩程序 常用 gzip 命令 五.zip 和 unzip:处理 ZIP 压缩文件 常用 zip 和 unzip 命令 实用技巧和最佳实践 六.结语 一.前言 在 Linux …...

BGP选路实验
要求: 1.如图连接网络,合理规格IP地址,AS200内IGP协议为OSPF; 2.R1属于AS 100;R2-R3-R4小AS234、R5-R6-R7小AS567,同时声明大AS 200,R8属于AS300; 3.R2-R5、R4-R7之间为联邦EBGP邻居…...

白骑士的C#教学高级篇 3.3 网络编程
网络编程是现代应用程序开发中至关重要的一部分。C# 提供了一套丰富的 API 来处理基本网络通信、Web请求与响应。在本节中,我们将深入探讨这些内容,帮助您掌握如何在 C# 中进行网络编程。 基本网络通信 基本网络通信通常涉及套接字(Socket&a…...

AI大模型赋能游戏:更智能、更个性化的NPC
参考论文:https://arxiv.org/abs/2403.10249 在传统游戏中,NPC(非玩家角色)的行为往往是预先设定好的,缺乏灵活性和变化性。然而,基于大模型的NPC可以利用其强大的推理和学习能力,实时生成对话…...

pymysql的上下文管理器:简化数据库操作
pymysql的上下文管理器:简化数据库操作 当我们使用 pymysql 操作数据库时,管理数据库连接和游标的生命周期是一项重要的任务。Python 的上下文管理器提供了一种优雅的方式来处理资源的获取和释放。在本文中,我们将探索如何创建一个简单的 py…...
)
AI秘境-墨小黑奇遇记 - 修炼成神经(二)
在解开了感知机和门电路的谜题后,墨小黑对人工智能的世界渐渐产生了浓厚的兴趣。他开始意识到,自己不仅是在学习一门复杂的技术,更是在探索一个充满未知与挑战的神秘领域。 入夜,墨小黑一脸无奈地盯着电脑屏幕,思考着自…...

计算机网络之分组交换时延的计算
一.类型 分组交换的时延包括一下几种: 1.1发送时延 发送时延,也叫传输时延,结点将分组的所有比特推向链路所需要的时间,即从发送分组的第一个比特算起,到该分组的最后一个比特发送完为止。 发送时延 分组长度 / 发…...
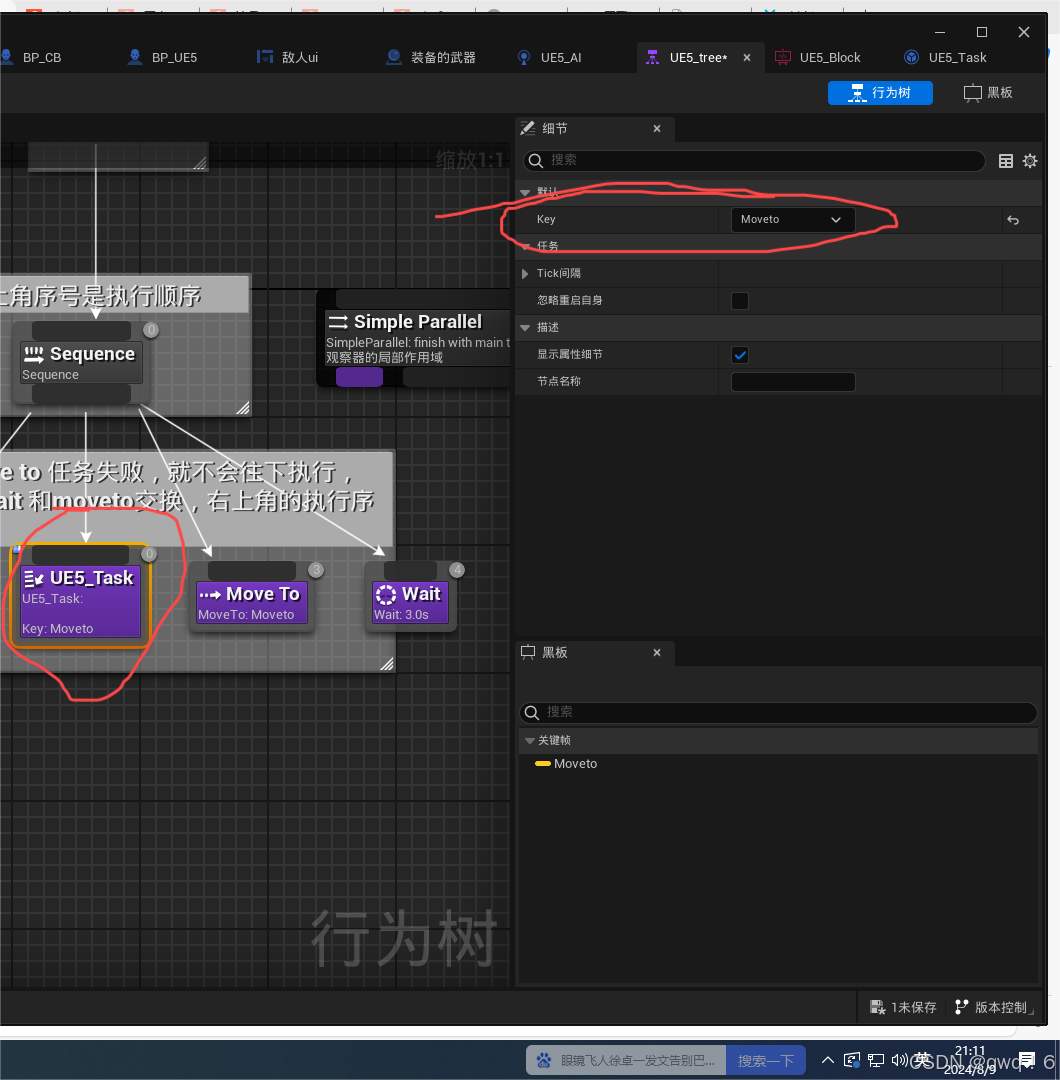
虚幻5|入门AI行为树,建立敌人
本章分成两块部分一块是第一点的制作一个简单的AI,后面第二点之后是第二部分建立ai行为树。这两个部分是一个衔接,最好不要跳看 一,制作一个简单的AI 1.首先,我们创建一个敌人的角色蓝图,添加一个场景组件widget用于…...

ARM处理架构中的PMU(Performance Monitoring Unit)和 AMU(Activity Monitors Unit)简介
在 ARM 架构中,PMU(Performance Monitoring Unit)和 AMU(Activity Monitors Unit)是用于性能分析和监控的硬件单元,但它们的功能和应用场景有所不同。以下是它们的主要区别: 1. PMU (Performance Monitoring Unit) 功能:PMU 是一种用于监控处理器性能的硬件单元。它可…...

Service服务在Android中的使用
目录 一,Service简介 二,Service的两种启动方式 1,非绑定式启动Service 2,绑定式启动Service 三,Service的生命周期 1,非绑定式Service的生命周期 2,绑定式Service的生命周期 四…...

浅谈C语言位段
1、位段的定义 百度百科中是这样解释位段的: 位段,C语言允许在一个结构体中以位为单位来指定其成员所占内存长度,这种以位为单位的成员称为“位段”或称“位域”( bit field) 。利用位段能够用较少的位数存储数据。 以下,我们均在VS2022的…...

arcgisserver登陆信息不正确
密码明明对,但是登录提示登录信息不正确 Arcgis server 9.3.1 无法登录ArcGIS Manager 提示Incorrect Login Information 操作系统windows 2008 x64server 解决办法: 关闭window防火墙解决。 如果防火墙已经关闭: 通过修改用户口令后就可以重…...

KOLA: CAREFULLY BENCHMARKING WORLD KNOWLEDGE OF LARGE LANGUAGE MODELS
文章目录 题目摘要简介KOLA 基准实验评估结论和未来工作道德声明 题目 KOLA:仔细对大型语言模型的世界知识进行基准测试 论文地址:https://arxiv.org/abs/2306.09296 项目地址:https://github.com/ranahaani/GNews 摘要 大型语言模型 (LLM) 的卓越性能要求评估方法…...

Robot Operating System——机器人关节的角度、速度和力矩
大纲 应用场景定义字段解释 案例 sensor_msgs::msg::JointState 是 ROS (Robot Operating System) 中的一个消息类型,用于表示机器人关节的状态信息。它通常用于传输和处理机器人关节的角度、速度和力矩等信息。 应用场景 机器人控制 关节控制:在机器人…...

一分钟掌握java9新特性
try-with-resources语句 /** * 在处理必须关闭的资源时,使用try-with-resources语句替代try-finally语句。 生成的代码更简洁,更清晰,并且生成的异常更有用 * java9 之前写法 */ public static String readFile1(String fileName){ tr…...

89. UE5 RPG 实现伤害 冷却 消耗技能描述
在上一篇文章里,我们能够通过富文本显示多种格式的文字,并显示技能描述。在这一篇文章里,我们继续优化技能描述,将技能说需要显示的内容显示出来。 实现火球术的基础描述 首先,我们现实现火球术的基础描述࿰…...

el-tree树状控件,定位到选中的节点的位置
效果图 在el-tree 控件加 :render-content"renderContent" 在掉接口的方法中 实际有用的是setTimeout 方法和this.$refs.xxxxxx.setCheckedKeys([industrycodeList]) if(res.data.swindustrylist.length>0){res.data.swindustrylist.forEach(item > {industry…...

YOLO目标检测的单目(多目标测距),使用相机光学模型,支持目标检测模型训练,可输出目标位置和距离信息并可视化
本项目旨在开发一个基于YOLO的目标检测系统,该系统不仅能检测图像中的多个目标,还能利用单目摄像头的图像估计每个目标与摄像头之间的相对距离。系统的核心组成部分包括目标检测、距离估计、模型训练以及结果可视化。 主要功能 目标检测:使用…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
