CTF密码学小结
感觉没啥好总结的啊
基础的永远是RSA、流密码、哈希、对称密码、古典密码那一套(密码学上过课都会),其他的就是数论的一些技巧
似乎格密码也很流行,以及一些奇奇怪怪的性质利用也很多
1、random设置种子后随机的性质:同一个种子生成同一个序列,如果把生成的序列中的某个数又作为种子,这样迭代生成的序列,只与第一条序列的种子相关
2、gcd(c,n)=gcd(c%n,n),ab%(ac) = a*(b%c)
3、yafu工具分解质因数,78位数分解约使用3分钟,非常好的工具,集成了试除法、fmt、pollar_rho、ecm等各种各样质因数分解方法,并且做了许多并行计算的优化,相当高效。
yafu-x64 "factor(@)" -batchfile 1.txt
把数字放在1.txt中,用换行隔开就可以了,注意末尾也需要是换行
4、一些有用的python函数和Crypto.Util.number库函数
str与字节编码串互相转换:(把‘abcd’转成b‘abcd’)a = a.encode(),a.decode()
长整数与字节编码串转换:long_to_bytes和bytes_to_long
bin(x)转换为二进制串(是str类型的,前面有0b开头)(注意二进制串的+是连接操作)
int(x,r)把字符串x按照r进制换算为数值
hex(x)获取十六进制的字符串
快速幂pow、求逆元inverse、GCD这些都是常用数论函数
5、数论的一些定理
(a,n互质)
20200601数论总结-CSDN博客
6、gmpy2使用iroot(x,r)对x开r次方,sympy使用sqrt_mod可以求二次剩余
7、看到数据范围小的一般是可以用于枚举的
8、RSA已知n和p+q就可以算出φ(n)
9、格理论
对一组线性无关的向量,他们的整数倍的线性组合构成一个格,这组向量称为格基
SVP问题,就是求格中范数最小的向量,CVP问题,就是给定一个向量,求格中的向量离他距离的最小值。复杂的都是O(a^k)级别的(a是常数,k是格基的大小(一般和向量维数相近))
格的基本区域:格基向量线性组合时,系数只为0、1时构成的集合,大小为2^k
相关博客:
格理论的基础知识-CSDN博客
格理论和密码学(一)-CSDN博客
ACD问题:有一组pi*q+ri,求q的值,有一系列解法:
格密码分析:正交格攻击 | tl2cents blog (tanglee.top)
10、sagemath在线网站:
Sage Cell Server (sagemath.org)
11、AES加密密钥一般是字符串,密文明文可以有hex编码与base64编码,注意区分
12、看到一大堆颜表情,先放到node-js里面跑一下,一般是aaencode或者jjencode编码
13、看到xesef-dovef-lesef-……这种类似的编码,BubbleBabble编码
14、利用数字串绘图,可以考虑折线、灰度图、塔珀自指公式(Tupper's Formula Tools (tuppers-formula.ovh))等方法
相关文章:
CTF密码学小结
感觉没啥好总结的啊 基础的永远是RSA、流密码、哈希、对称密码、古典密码那一套(密码学上过课都会),其他的就是数论的一些技巧 似乎格密码也很流行,以及一些奇奇怪怪的性质利用也很多 1、random设置种子后随机的性质:…...
——Vue3 状态管理 - Pinia(二))
Vue快速入门(七)——Vue3 状态管理 - Pinia(二)
目录 六、核心概念——Getter 1、基本操作 定义getter 访问getter 2、访问其他 getter 3、向 getter 传递参数 4、访问其他 store 的 getter 使用 setup() 时的用法 使用选项式 API 的用法 使用 setup() 不使用 setup() 七、核心概念——Action 1、基本操作 定义a…...

ZooKeeper集群环境部署
1. ZooKeeper安装部署 1.1 系统要求 1.1.1 支持的平台 ZooKeeper 由多个组件组成。一些组件得到广泛支持,而另一些组件仅在较小的一组平台上得到支持。 客户端是 Java 客户端库,由应用程序用于连接到 ZooKeeper 集群。 服务器是在 ZooKeeper 集群节点…...

10 个 C# 关键字和功能
在 Stack Overflow 调查中,C# 语言是排名第 5 位的编程语言。它广泛用于创建各种应用程序,范围从桌面到移动设备再到云原生。由于有如此多的语言关键字和功能,对于开发人员来说,要跟上新功能发布的最新信息将是一项艰巨的任务。本…...

贪心算法之重叠区间问题
以下四个题都是重叠区间问题 452. 用最少数量的箭引爆气球 为了让气球尽可能重叠,先按照气球起始位置由大到小排序tips:sort默认就可以实现以上排序,不需要写cmp重点:当下一个气球的左边界不小于上一个气球的右边界时(即有重叠的…...

Python爬虫入门教程(非常详细)适合零基础小白
一、什么是爬虫? 1.简单介绍爬虫 爬虫的全称为网络爬虫,简称爬虫,别名有网络机器人,网络蜘蛛等等。 网络爬虫是一种自动获取网页内容的程序,为搜索引擎提供了重要的数据支撑。搜索引擎通过网络爬虫技术,将…...

ArcGIS Pro基础:软件的常用设置:中文语言、自动保存、默认底图
上图所示,在【选项】(Options)里找到【语言】设置,将语言切换为中文选项,记得在安装软件时,需要提前安装好ArcGIS语言包。 上图所示,在【选项】里找到【编辑】设置,可以更改软件默认…...

依赖注入+中央事件总线:Vue 3组件通信新玩法
🌈个人主页:前端青山 🔥系列专栏:Vue篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来Vue篇专栏内容:Vue-依赖注入-中央事件总线 目录 中央事件总线使用 依赖注入使用 总结 中央事件总线 依赖注入…...
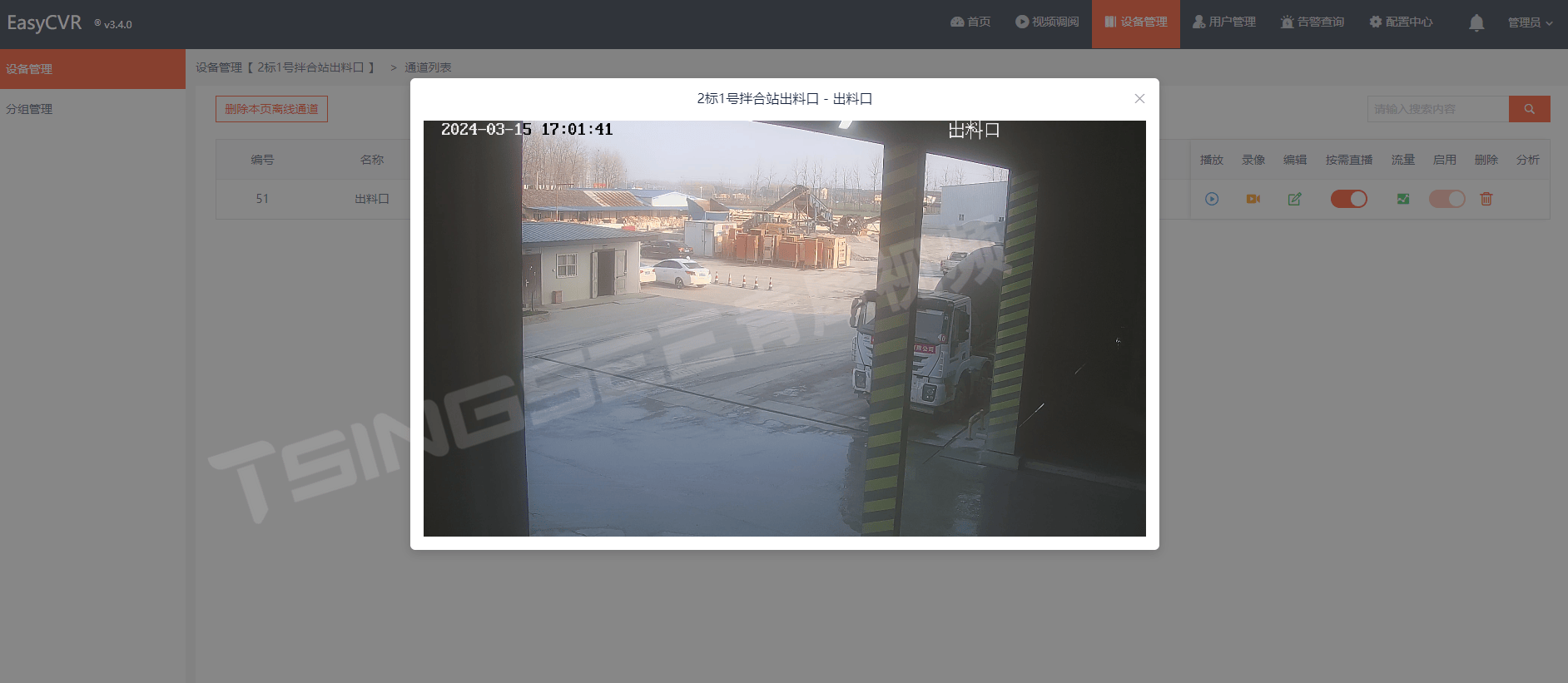
EasyCVR视频汇聚平台构建远程安防监控:5大亮点解析,助力安防无死角
随着科技的飞速发展,远程安防监控系统已经成为现代社会中不可或缺的一部分,无论是在小区、公共场所还是工业领域,安防监控都发挥着至关重要的作用。而EasyCVR作为一款功能强大的视频监控综合管理平台,其在构建远程安防监控系统方面…...

fastadmin安装插件报500的错误
项目场景: 项目新建后,想在本地项目中安装相关的插件,但是在插件管理页面点击安装的时候一直报500的错误。 问题描述 我们将项目中的调试打开,在application/config.php里修改 app_debug,将false改为true,…...

速盾:为什么需要服务器和cdn?
在互联网时代,服务器和CDN(内容分发网络)起着非常重要的作用。它们是实现高效、稳定和可靠网络服务的关键组成部分。下面我将详细阐述为什么需要服务器和CDN。 首先,服务器是互联网上存储、处理和传输数据的中心枢纽。当我们在浏…...

十四、模拟实现 list 类
Ⅰ . list 基本框架的实现 01 结点的建立 为了实现链表,我们首先要做的应该是建立结点 为了和真正的 list 进行区分,我们仍然在自己的命名空间内实现 代码实现: namespace yxt {// 建立结点template<class T>struct ListNode{T _d…...

JavaScript简介之引入方式
JavaScript 引入方式 提问:CSS的引入方式?在学习 JavaScript 语法之前,我们首先要知道在哪里写 JavaScript 才行。想要在 HTML 中引入 JavaScript,一般有 3 种方式。 外部 JavaScript 内部 JavaScript 元素事件 JavaScript&#…...

同一台电脑上安装不同版本的nodejs(搭配VSCode)
今天拉取了一个前后端分离的项目,运行前端的时候,出现node版本不匹配的情况。 本文章将从安装node.js开始到VSCode使用进行讲解 1、去官网下载node版本 以16版本为例,需要哪个版本,就在网址上把版本号替换即可 https://nodejs.o…...
python小游戏之摇骰子猜大小
最近学习Python的随机数,逻辑判断,循环的用法,就想找一些练习题,比如小游戏猜大小,程序思路如下: 附上源代码如下: 摇骰子的函数,这个函数其实并不需要传任何参数,调用后…...

C++入门——12继承
1.继承 继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段,它允许程序员在保持原有类特性的基础上进行扩展,增加功能,这样产生新的类,称派生类。继承呈现了面向对象程序设计的层次结构,体现了由简…...

Python做统计图之美
Python数据分析可视化 案例效果图 import pandas as pd import matplotlib.pyplot as plt import matplotlib# 数据 data {"房型": [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],"住宅类型": ["普通宅", "普通宅", "普通宅", &q…...

激光雷达点云投影到图像平面
将激光雷达点云投影到图像平面涉及几何变换和相机模型的应用。以下是该过程的基本原理: 1. 坐标系转换 激光雷达生成的点云通常位于激光雷达的坐标系中,而图像则在相机坐标系中。为了将点云投影到图像上,首先需要将点云从激光雷达坐标系转换…...

[python]将anaconda默认创建环境python版本设置为32位的
首先看看gpt怎么回答的 装了Anaconda。如果尚未安装,可以从Anaconda官网下载适合你的操作系统的安装程序,并按照安装向导进行安装。 二、创建32位Python环境 在Anaconda中,你可以通过修改环境变量来尝试切换到32位模式(尽管这并…...
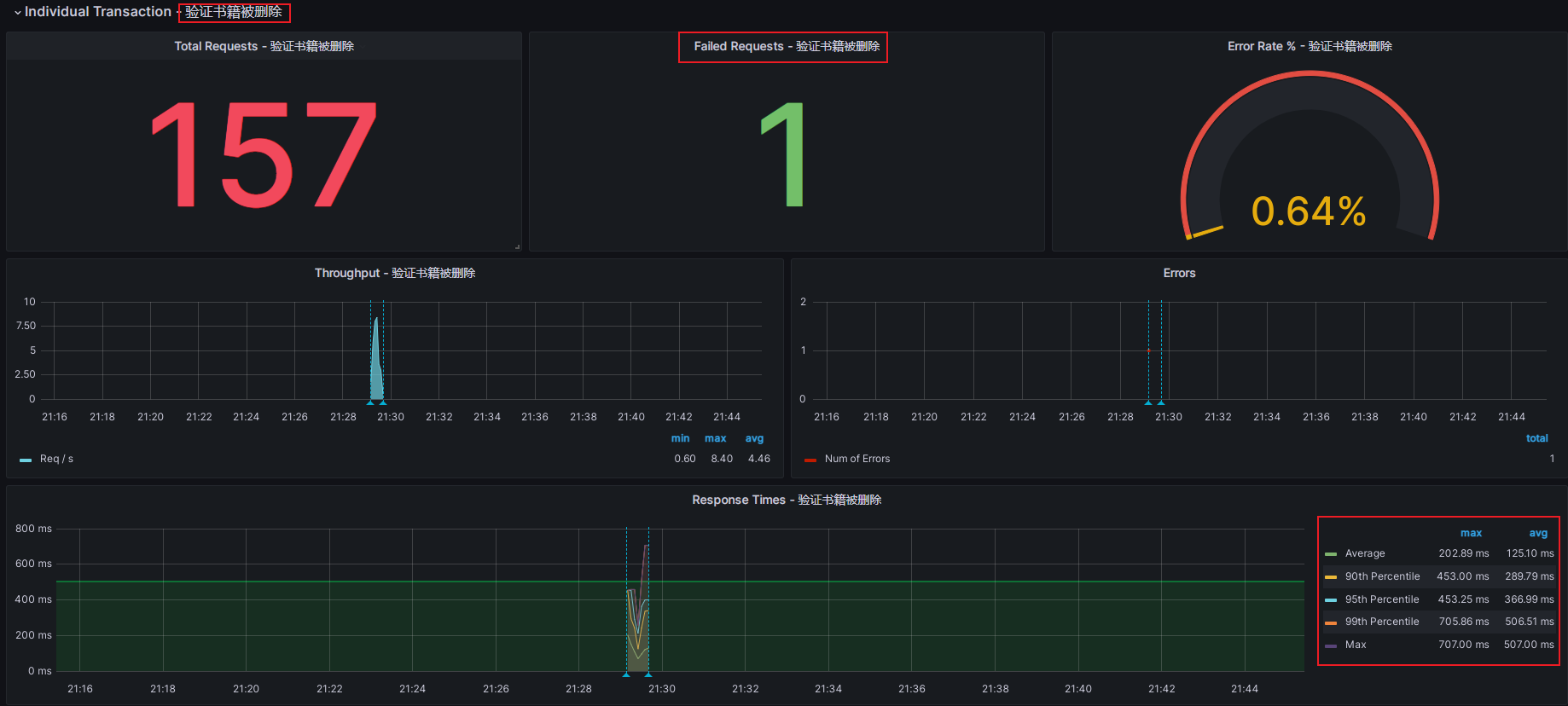
Jmeter+Influxdb+Grafana平台监控性能测试过程(三种方式)
一、Jmeter自带插件监控 下载地址:Install :: JMeter-Plugins.org 安装:下载后文件为jmeter-plugins-manager-1.3.jar,将其放入jmeter安装目录下的lib/ext目录,然后重启jmeter,即可。 启动Jmeter,测试计…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
