【数据结构】哈希表

目录
1、哈希表
1.1 哈希表的简介
1.2 降低哈希冲突率
1.3 解决哈希冲突
1.3.1 闭散列
1.3.2 开散列(哈希桶)
1、哈希表
1.1 哈希表的简介
假设我们目前有一组数据,我们要从这组数据中找到指定的 key 值,那么咱们目前的学习阶段可以利用三种方法:
- 把数据存储在数组当中,按顺序依次查找,时间复杂度为 O(n)
- 把数据存储在数组当中,此时数组有序,则可以用二分查找法,时间复杂度为 O(logn)
- 将其转化成搜索树进行查找,时间复杂度为 O(logn)
除了上述的查找方式以外,是否还有比上述查找方式的时间复杂度更优的呢?
答:有,还有一种方式可以做到查找时间复杂度为 O(1),这种方式就是用哈希表进行查找
哈希方法:通过某种函数使元素的存储位置与它的关键码(元素)之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素,不经过任何比较,一次直接从表中得到要搜索的元素
哈希函数和哈希表:哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表
- 插入操作:插入元素根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放
- 搜索操作:对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则搜索成功
例如:假设我们现在有这样一种数据集合{1,6,7,5,4,9}
哈希函数设置为:hash = key % capacity
- hash:位置
- key :数据值
- capacity:数组长度
哈希表的长度为:10

假设我们现在要将第一个元素 1,放进哈希表中,首先通过哈希函数确定插入的位置 hash = 1%10那么此时 1 插入的位置也就是哈希表中下标为 1 的位置,其他元素也都是按照同样的方式进行存放到哈希表中

当我们进行搜索操作的时候也是通过哈希函数进行搜索的,假设我们现在需要查找 6 这个元素所在的位置,hash = key % capacity 也就是 6 % 10 = 6,此时 6 这个元素所在的位置就在 6 下标
假设我们目前需要在上述哈希表中插入 11 ,通过哈希函数找到的下标位置为 1,然后此时 1 下标的位置已经有值了,此时也就造成了哈希冲突问题了
哈希冲突:不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞
哈希冲突产生的原因:由于我们哈希表底层数组的容量往往是小于实际要存储的关键字的数量的,这就导致一 个问题,冲突的发生是必然的,但我们能做的应该是尽量的降低冲突率
1.2 降低哈希冲突率
那如何降低哈希冲突呢?
1.设计合理的哈希函数(哈希函数往往并不是由我们设计的,而是由专业人员进行设计的)
哈希函数设计原理:
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1 之间 哈希函数计算出来的地址能均匀分布在整个空间中 哈希函数应该比较简单
- 哈希函数计算出来的地址能均匀分布在整个空间中
- 哈希函数应该比较简单
常见的哈希函数,目前咱们也就只介绍两个:
- 直接定制法:取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B。 优点:简单、均匀 缺点:需要事先知道关键字的分布情况 使用场景:适合查找比较小且连续的情况
- 除留余数法:设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数: Hash(key) = key% p(p<=m),将关键码转换成哈希地址
2.调节负载因子
负载因子 = 填入表中的元素个数 / 表的长度
负载因子的作用:

通过上述图就可以看出当负载因子越大时,冲突率也是越高的
那如何调节负载因子呢?
答:已知填入表中的元素个数是不变的,那么就只能调整哈希表的数组长度了。当数组长度越长,那么负载因子也就越小
一般情况下,哈希表会有一个默认的负载因子值为 0.75f
设计合理函数和调节负载因子也不能完全避免冲突 ,那么此时就可以解决哈希冲突
1.3 解决哈希冲突
解决哈希冲突常见的方法是:闭散列 和 开散列
1.3.1 闭散列
闭散列(开放地址法):当发生哈希冲突时,如何哈希表未被装满还有空余的位置,那么就可以将元素 key 存放到冲突位置中的 “下一个” 空位置中
那么我们应该如何找到下一个空位置呢?
方法一:线性探测法
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止
插入:
- 通过哈希函数获取待插入元素在哈希表中的位置
- 如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探测找到 下一个空位置,插入新元素

假设我们要在上述的哈希表中插入11,通过哈希函数确定的位置是下标 1,但是下标 1 的位置此时有元素发生了哈希冲突,使用线性探测找到的下一个空位置为下标2的位置,则把11 插入到下标2的位置 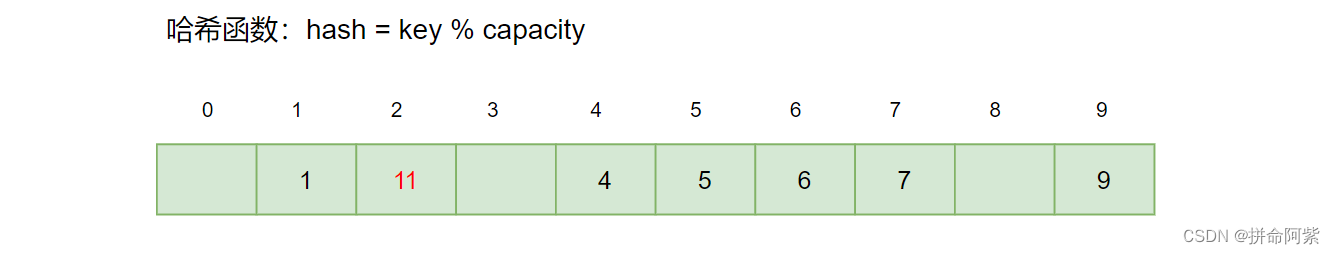
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素会影响其他 元素的搜索。比如删除元素1,如果直接删除掉,11查找起来可能会受影响。因此线性探测采用标 记的伪删除法来删除一个元素。
方法二:二次探测法
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式就是挨 着往后逐个去找,因此二次探测为了避免该问题,找下一个空位置的方法为:


假设我们现在需要在上述表中插入元素 11,通过哈希函数确定的位置是下标 1,但是下标 1 的位置此时有元素发生了哈希冲突,这是与 下标1 位置发生的第一次冲突:(11 + 1*1)% 10 = 2。那么此时元素 11 插入的位置就是下标2的位置
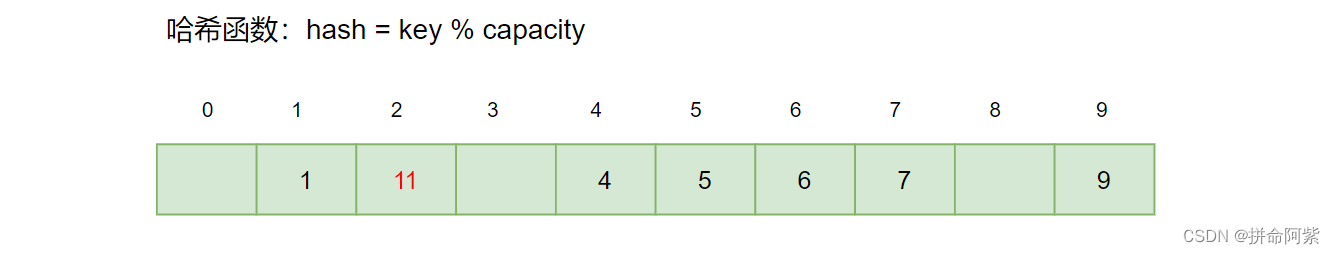
研究表明:当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不 会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情 况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容
闭散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷
1.3.2 开散列(哈希桶)
开散列:开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中
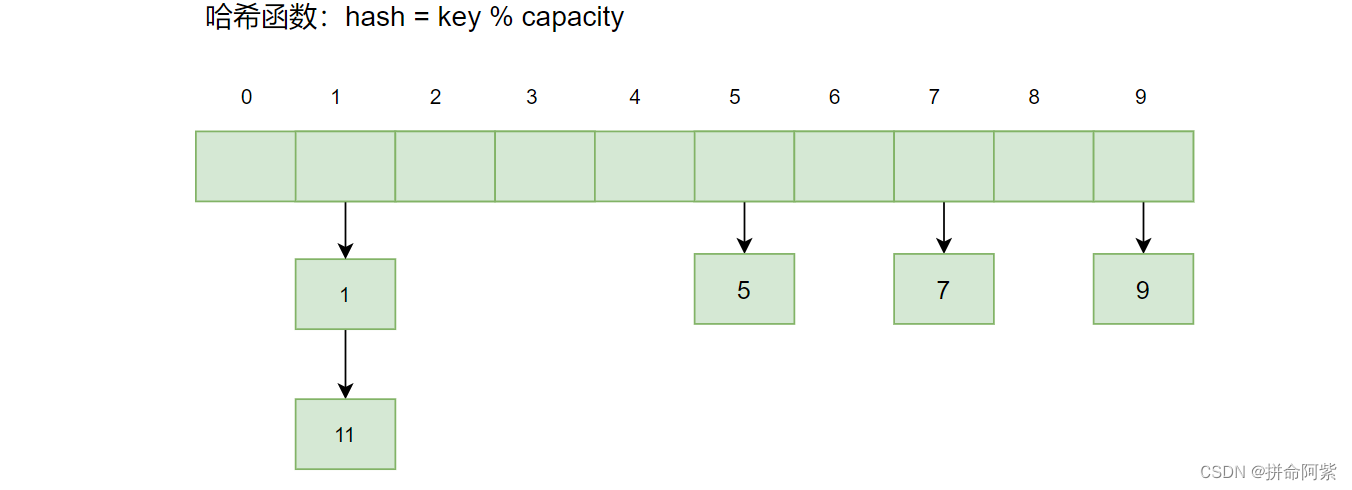
- JDK1.7版本及以前每个桶使用的是头插法
- JDK1.8版本及以后每个桶使用的是尾插法
开散列可以认为是把一个在大集合中的搜索问题转化为在小集合中做搜索了
那会不会哈希表中一个桶的长度太长,而导致搜索效率为 O(n)呢?
答:应该不会,因为有负载因子,当一个桶的长度太长时,会进行扩容
hashMap就是采用开散列的方式进行处理的, 当哈希表的长度到达64且桶的长度到底8时,会转换成红黑树
虽然哈希表一直在和冲突做斗争,但在实际使用过程中,我们认为哈希表的冲突率是不高的,冲突个数是可控的, 也就是每个桶中的链表的长度是一个常数,所以,通常意义下,我们认为哈希表的插入/删除/查找时间复杂度是 O(1)
相关文章:

【数据结构】哈希表
目录 1、哈希表 1.1 哈希表的简介 1.2 降低哈希冲突率 1.3 解决哈希冲突 1.3.1 闭散列 1.3.2 开散列(哈希桶) 1、哈希表 1.1 哈希表的简介 假设我们目前有一组数据,我们要从这组数据中找到指定的 key 值,那么咱们目…...

物联网常用协议MQTT协议相关介绍
概述 MQTT(Message Queuing Telemetry Transport)是一种轻量级的消息传输协议,旨在在网络带宽有限的情况下,为物联网设备之间的通信提供可靠的、低延迟的消息传递服务。MQTT协议具有订阅/发布模式,支持多种传输协议&a…...

【C语言进阶】13. 假期测评②
day10 1. int类型字节数 求函数返回值,传入 -1 ,则在64位机器上函数返回( ) int count 0; int x -1; while (x) {count;x x >> 1; } printf("%d", count);A: 1 B: 2 C: 32 D: 死循环,没结果 【答案解析】C xx&(x-1)这…...

【国产FPGA】国产FPGA搭建图像处理平台
最近收到了高云寄过来的FPGA板卡,下图:来源:https://wiki.sipeed.com/hardware/zh/tang/tang-primer-20k/primer-20k.htmlFPGA主要参数:FPGA型号参数GW2A-LV18PG256C8/I7逻辑单元(LUT4) 20736寄存器(FF) 15552分布式静态随机存储器S-SRAM(bit…...
你的应用太慢了,给我司带来了巨额损失,该怎么办
记得很久之前看过谷歌官方有这么样的声明:如果一个页面的加载时间从 1 秒增加到3 秒,那么用户跳出的概率将增加 32%。 但是早在 2012 年,亚马逊就计算出了,页面加载速度一旦下降一秒钟,每年就会损失 16 亿美元的销售额…...

第十四届蓝桥杯三月真题刷题训练——第 22 天
目录 第 1 题:受伤的皇后_dfs 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思路: 第 2 题:完全平方数 问题描述 输入格式 输出格式 样例输入 1 样例输出 1 样例输入 2 样例输出 2 评测用例规模与约…...
机器学习:朴素贝叶斯模型算法原理(含实战案例)
机器学习:朴素贝叶斯模型算法原理 作者:i阿极 作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏&…...

Linux 多线程:理解线程
目录一、理解线程的思想二、Linux中的线程与进程1.Linux中的进程2.Linux中的线程三、线程的工作方式四、线程的独有数据与共享数据1.独有数据2.共享数据一、理解线程的思想 线程就是把一个进程分成多个执行部分,一个部分就是一个线程,比如可以让一个线程…...
Web前端学习:章四 -- JavaScript初级(四)-- BOM
138:Object数据格式简介 1、object对象 JS中独有 的一种数据格式 名字可以随便取,值一般就那几种数据格式 139:BOM - JS跳转页面 BOM Browser Object Model:浏览器对象模型 使用JavaScript控制浏览器交互 控制浏览器里面的内…...

Lesson9.网络基础1
网络协议初识 所谓的协议就是人们为了通信的一种约定 操作系统要进行协议管理,必然会先描述,再组织协议本质就是软件,软件是可以"分层"协议在设计的时候,就是被层状的划分的, 为什么要划分成为层状结构 场景复杂功能解耦(便于人们进行各种维护)OSI七层模型 局域网中…...
这几个SQL语法的坑,你踩过吗
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

算法基础——复杂度
前言 算法是解决问题的一系列操作的集合。著名的计算机科学家Niklaus Wirth曾提出:算法数据结构程序,由此可见算法在编程中的重要地位。本篇主要讨论算法性能好坏的标准之一——复杂度。 1 复杂度概述 1.1 什么是复杂度 本文所讨论的复杂度是指通过事先…...

基类与派生类对象的关系 派生类的构造函数
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...
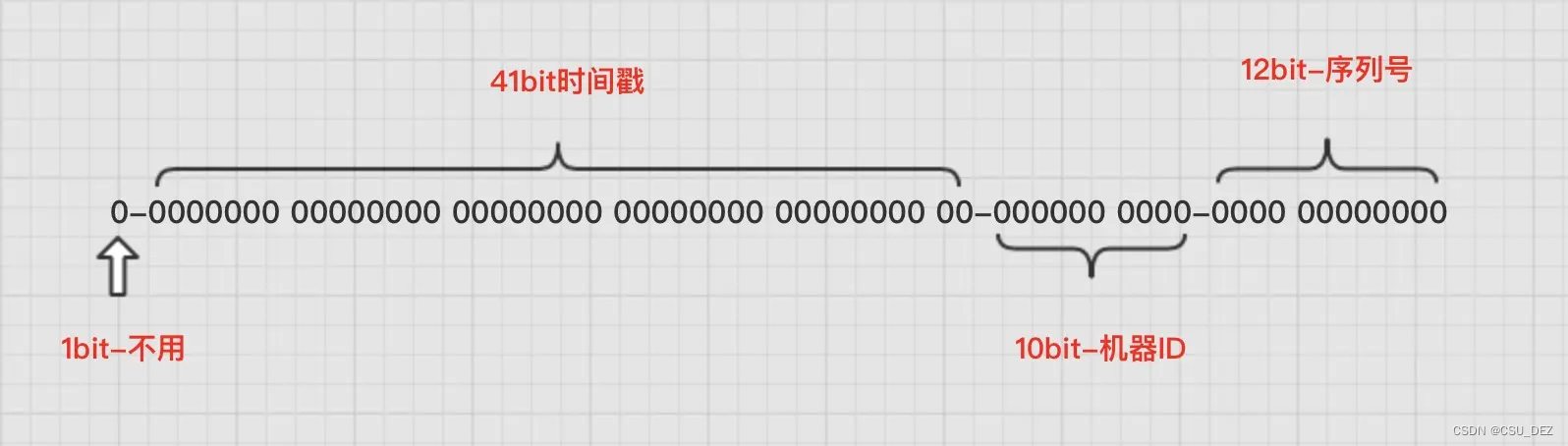
【算法】生成分布式 ID 的雪花算法
ID 是数据的唯一、不变且不重复的标识,在查询数据库的数据时必须通过 ID 查询,在分布式环境下生成全局唯一的 ID 是一个重要问题。 雪花算法(snowflake)是一种生成分布式环境下全局唯一 ID 的算法,该算法由 Twitter 发…...
Linux系统编程 - 基础IO(IO操作)
目录 预备知识 复习C文件IO相关操作 printf相关函数 fprintf snprintf 读取文件 系统文件IO操作 open函数 umask()函数 open函数返回值 预备知识 1.你真的理解文件原理和操作了吗?不是语言问题,是系统问题2.是不是只有C/C有文件操作呢&#x…...

基于 Avue 的 CRUD 表格组件封装
在 components 文件夹中,创建一个新的 .vue 文件,例如:AvueCrudTable.vue。 透传父组件传递的属性和事件 : 1、利用v-bind=“ a t t r s " 支持所有 a v u e 的使用方法并在其基础上进行封装 2 、使用 v − o n = " attrs"支持所有 avue 的使用方法并在其基…...
基于框架编写驱动代码)
树莓派学习笔记(十三)基于框架编写驱动代码
文章目录一、代码分析:二、源码一、代码分析: 在内核中由于代码文件多,避免函数名重复,使用static将函数的作用域限制在该文件内 内核的打印函数printk和printf类似 file_operations结构体使用符号“ . ”指定参数,省…...
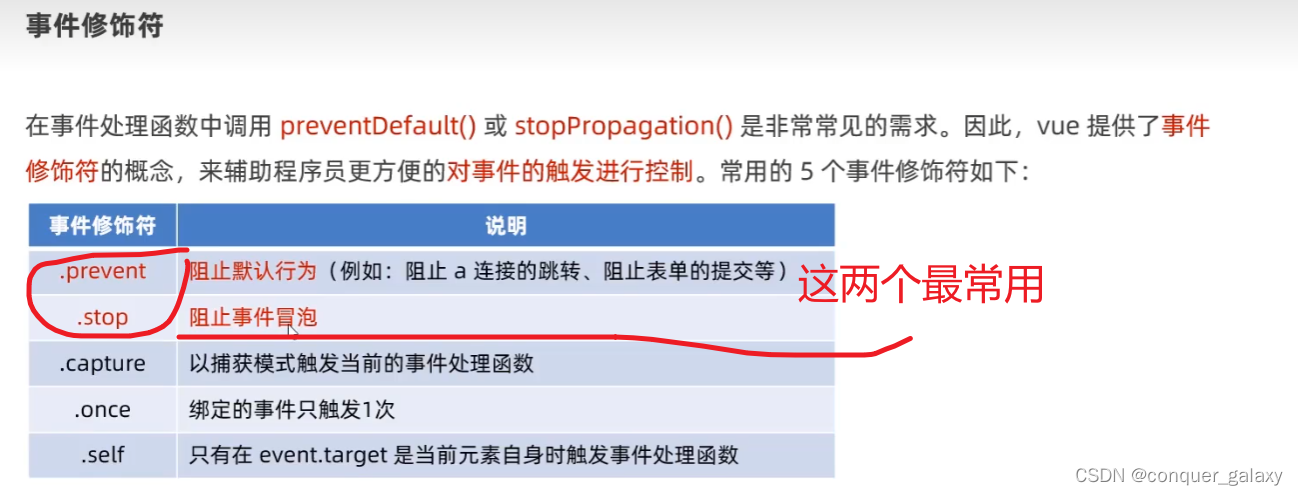
vue事件修饰符之.prevent
.prevent 事件修饰符只是阻止默认事件,不会自动触发任何事件处理函数。因此,在使用 .prevent 事件修饰符时,需要自己编写相应的事件处理函数来处理事件。 例如,在上面的例子中,我们通过在表单上绑定 submit.prevent&q…...

【SpringCloud AlibabaSentinel实现熔断与限流】
本笔记内容为尚硅谷SpringCloud AlibabaSentinel部分 目录 一、Sentinel 1、官网 2、Sentinel是什么 3、下载 4、特性 5、使用 二、安装Sentinel控制台 1、sentinel组件由2部分构成 2、安装步骤 1.下载 2.运行命令 3.访问sentinel管理界面 三、初始化演示工程 …...

类与对象-封装
一、封装的意义封装是C面向对象三大特性之一语法: class name { 访问权限:属性行为 };注意:类中的属性和行为 统称为成员属性 又称 成员属性 / 成员变量行为 又称 成员函数 / 成员方法封装将属性和行为作为一个整体,表现生活中的事物例①&…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
