递归--数据结构--黑马
递归
总结一句话,上手直接多刷Leetcode,比看这个更有用。
定义
递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集。
例如,单链表递归遍历的例子:
void f(Node node) {if (node == null) {return;}f(node.next);
}
说明:
- 自己调用自己,如果每个函数对应一个解决方案,自己调用自己意味着解决方案一样(有规律)。
- 每次调用,函数处理的数据会较上次缩减(子集),而且最后会缩减至无需继续递归。
- 内层函数调用(子集处理)完成,外层函数才能算调用完成。
例如,
// 假如链表是,1 -> 2 -> 3 -> null
void f(Node node) {if (node == null) {return;}System.out.println("before: " + node.value);f(node.next);System.out.println("after: " + node.value);
}
根据递归的性质,从链表头节点开始遍历,打印第一个节点值 n o d e . v a l u e = 1 node.value=1 node.value=1 ,进入 f ( n o d e . n e x t ) f(node.next) f(node.next) 第二个节点不为空,打印第二个节点值 n o d e . v a l u e = 2 node.value=2 node.value=2 ,进入 f ( n o d e . n e x t ) f(node.next) f(node.next) 到第三个节点(不为null),打印第三个节点值 n o d e . v a l u e = 3 node.value=3 node.value=3 ,进入 f ( n o d e . n e x t ) f(node.next) f(node.next) ,因为当前节点为null,则进入 i f if if 语句,return返回,执行第三次 f f f 函数的输出语句,得到 n o d e . v a l u e = 3 node.value=3 node.value=3 ,然后执行第二次 f f f 函数的输出语句,得到 n o d e . v a l u e = 2 node.value=2 node.value=2 ,最后执行第一次 f f f 函数的输出语句,得到 n o d e . v a l u e = 1 node.value=1 node.value=1 。
使用伪代码执行流程如下,不考虑语法正确。
// 假如链表是,1 -> 2 -> 3 -> null
void f(Node node = 1) {System.out.println("before: " + node.value); // 1void f(Node node = 2) {System.out.println("before: " + node.value); // 2void f(Node node = 3) {System.out.println("before: " + node.value); // 3void f(Node node = null) {if (node == null) {return;}}System.out.println("after: " + node.value); // 3}System.out.println("after: " + node.value); // 2}System.out.println("after: " + node.value); // 1
}
简单应用
例1 - 阶乘
用递归方法求阶乘
- 阶乘定义: n ! = 1 ⋅ 2 ⋅ 3 ⋯ ( n − 2 ) ⋅ ( n − 1 ) ⋅ n n!=1·2·3 \cdots(n-2)·(n-1)·n n!=1⋅2⋅3⋯(n−2)⋅(n−1)⋅n ,其中 n n n 为自然数, 0 ! = 1 0!=1 0!=1 。
- 递推关系
f ( n ) = { 1 , n = 1 n ∗ f ( n − 1 ) , n > 1 f(n) = \begin{cases} 1, & n=1 \\ n*f(n-1), & n>1 \end{cases} f(n)={1,n∗f(n−1),n=1n>1
public class Factorial {public int f(int n) {if (n == 1) {return 1;}return n * f(n - 1);}
}
例2 - 递归反向打印字符串
public class ReversePrintString{public static void f(int n, String str) {if (n == str.length()) { // 当n索引等于字符串长度,returnreturn;}f(n + 1, str);System.out.println(str.charAt(n));}public static void main(String[] args) {f(0, "abcd");}
}
例3 - 递归版二分查找
public class BinarySearch {public static int search(int[] a, int target) {return f(a, target, 0, a.length - 1);}// 实现递归的方法private static int f (int[] a, int target, int i, int j) {if (i > j) {// 递归终止条件,未找到return -1;}int m = (i + j) >>> 1;if (target < a[m]) {return f(a, target, i, m - 1);} else if (target > a[m]) {return f(a, target, m + 1, j);} else {return m;}}}
例4 - 递归版冒泡排序
public class BubbleSort{public static void sort (int[] a) {bubble(a, a.length - 1);}private static void bubble(int[] a, int j) {if (j == 0) {return;}for(int i = 0; i < j; i++) {if (a[i] > a[i + 1]) {swap(a, i, i + 1);}}bubble(a, j - 1);}public static void swap(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}
}
递归版冒泡排序改进
public class BubbleSort{public static void sort (int[] a) {bubble(a, a.length - 1);}private static void bubble(int[] a, int j) {if (j == 0) {return;}int x = 0; // 使用变量x记录下次排序的右边界for(int i = 0; i < j; i++) {if (a[i] > a[i + 1]) {swap(a, i, i + 1);x = i;}}bubble(a, x);}public static void swap(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}
}
或者不使用递归,直接使用循环,如下
public class BubbleSort{public static void sort (int[] a) {int j = a.length - 1;while (true) {int x = 0; // 使用变量x记录下次排序的右边界for(int i = 0; i < j; i++) {if (a[i] > a[i + 1]) {swap(a, i, i + 1);x = i;}}j = x;if (j == 0) {break;}}}public static void swap(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}public static void main(String[] args) {int[] arr = {9, 8, 7, 6, 5, 4, 3, 2, 1};sort(arr);System.out.println(Arrays.toString(arr));}
}
例5 - 递归版插入排序
public class InsertionSort{public static void sort(int[] a) {insertion(a, 1);}public static void insertion(int[] a, int low) {if (low == a.length) {return;}int t = a[low];int i = low - 1;while (i >= 0 && a[i] > t) {a[i + 1] = a[i];i--;}if (low - 1 != i) {a[i + 1] = t;}insertion(a, low + 1);}}
不使用递归,直接使用循环,如下
public class InsertionSort{public static void sort(int[] a) {for(int low = 1; low < a.length; low++) {int t = a[low]; // 插入的值int i = low - 1; // 已排序的右边界while (i >= 0 && a[i] > t) {a[i + 1] = a[i];i--;}// 找到插入点,找到比插入值小的索引if (low - 1 != i) {a[i + 1] = t;}}}
}
例6 - 斐波那契数列
递推关系
f ( n ) = { 0 , n = 0 1 n = 1 f ( n − 1 ) + f ( n − 2 ) , n > 1 f(n) =\begin{cases}0,& n=0\\ 1 & n=1 \\ f(n - 1)+f(n-2), & n>1 \end{cases} f(n)=⎩ ⎨ ⎧0,1f(n−1)+f(n−2),n=0n=1n>1
public class Fibonacci {public static int f(int n) {if (n == 0) {return 0;}if (n == 1) {return 1;}return f(n - 1) + f(n - 2);}
}
改进算法如下,使用空间换时间
public class Fibonacci {public static int fibonacci (int n) {int[] cache = new int[n + 1];Arrays.fill(cache, -1);cache[0] = 1;cache[1] = 1;return f(n, cache);}public static int f (int n, int[] cache) {if (cache[n] != -1) {return cache[n];} cache[n] = f(n - 1) + f(n - 2);return cache[n];}
}
递归时间复杂度计算
Master theorem 主定理
若有递归式
T ( n ) = a T ( n b + f ( n ) ) T(n)=aT(\frac{n}{b} + f(n)) T(n)=aT(bn+f(n))
其中
- T ( n ) T(n) T(n) 是问题运行的时间, n n n 是数据规模
- a 是子问题个数
- T ( n b ) T(\frac{n}{b}) T(bn) 子问题运行的时间,每个子问题被拆成原问题数据规模的 n b \frac{n}{b} bn
- f ( n ) f(n) f(n) 是除去递归外运行的时间。
令 x = l o g b a x=log_{b}a x=logba ,即 x = l o g 子问题缩小倍数 x=log_{子问题缩小倍数} x=log子问题缩小倍数 子问题个数
那么
T ( n ) = { Θ ( n x ) f ( n ) = O ( n c ) 并且 c < x Θ ( n x l o g n ) f ( n ) = Θ ( n x ) Θ ( n c ) f ( n ) = Ω ( n c ) 并且 c > x T(n) = \begin{cases} \Theta(n^x) & f(n)=O(n^c)并且c<x\\ \Theta(n^xlogn) & f(n)=\Theta(n^x)\\ \Theta(n^c) & f(n)=\Omega(n^c)并且c>x \end{cases} T(n)=⎩ ⎨ ⎧Θ(nx)Θ(nxlogn)Θ(nc)f(n)=O(nc)并且c<xf(n)=Θ(nx)f(n)=Ω(nc)并且c>x
例 1
T ( n ) = 2 T ( n 2 + n 4 ) T(n)=2T(\frac{n}{2} + n^4) T(n)=2T(2n+n4)
- x = 1 < 4 x=1<4 x=1<4 ,由后者决定时间复杂度 Θ ( n 4 ) \Theta(n^4) Θ(n4) 。
例 2
T ( n ) = T ( 7 n 10 + n 4 ) T(n)=T(\frac{7n}{10} + n^4) T(n)=T(107n+n4)
- x = 0 < 1 x=0<1 x=0<1 ,由后者决定时间复杂度 Θ ( n ) \Theta(n) Θ(n) 。
例 3
T ( n ) = 16 T ( n 4 + n 2 ) T(n)=16T(\frac{n}{4} + n^2) T(n)=16T(4n+n2)
- x = 2 = 2 x=2=2 x=2=2 ,由前者决定时间复杂度 Θ ( n 2 l o g n ) \Theta(n^2logn) Θ(n2logn) 。
例 4 - 递归-二分查找
public static int f(int[] a, int target, int i, int j) {int m = (i + j) >>> 1;if (i > j) {return - 1;}if (target < a[m]) {return f(a, target, i, m - 1);} else if (target > a[m]) {return f(a, target, m + 1, j);} else {return m;}
}
- 子问题个数 a = 1 a=1 a=1 ;
- 子问题数据规模缩小倍数 b = 2 b = 2 b=2 ;
- 除递归外执行的计算是常数级 c = 0 c=0 c=0 ;
T ( n ) = T ( n 2 + n 0 ) T(n)=T(\frac{n}{2} + n^0) T(n)=T(2n+n0)
- 因为 x = 0 = 0 x=0=0 x=0=0 ,时间复杂度为 Θ ( l o g n ) \Theta(logn) Θ(logn) 。
例 5 - 递归-归并排序
// 伪代码
void split(B[], i, j, A[]) {if (j - i <= 1) {return;}m = (i + j) >>> 1;// 递归split(B[], i, m - 1, A[]);split(B[], m + 1, j, A[]);// 合并merge(B, i, m, j, A);
}
- 子问题个数 a = 2 a=2 a=2 ;
- 子问题数据规模缩减倍数 b = 2 b=2 b=2;
- 除递归外,主要时间花在合并上,用 f ( n ) = n f(n)=n f(n)=n 表示;
T ( n ) = 2 T ( n 2 + n ) T(n)=2T(\frac{n}{2} + n) T(n)=2T(2n+n)
- 因为 x = 1 = 1 x=1=1 x=1=1 ,时间复杂度为 Θ ( n l o g n ) \Theta(nlogn) Θ(nlogn) 。
展开定理
例 1 - 递归求和
long sum(long n) {if (n == 1) {return 1;}return sum(n - 1) + n;
}
T ( n ) = T ( n − 1 ) + c T(n)=T(n - 1) + c T(n)=T(n−1)+c , T ( 1 ) = c T(1)=c T(1)=c
如下展开过程
T ( n ) = T ( n − 2 ) + c + c T(n)=T(n - 2) + c + c T(n)=T(n−2)+c+c
T ( n ) = T ( n − 3 ) + c + c + c T(n)=T(n - 3) + c + c + c T(n)=T(n−3)+c+c+c
⋯ \cdots ⋯
T ( n ) = T ( 1 ) + ( n − 1 ) c = n c T(n)=T(1)+(n-1)c=nc T(n)=T(1)+(n−1)c=nc
时间复杂度: O ( n ) O(n) O(n)
例 2 - 递归冒泡排序
void bubble(int[] a, int high) {if (high == 0) {return;}for(int i = 0; i < high; i++) {if (a[i] > a[i + 1]) {// 交换swap(a, i, i + 1);}}return bubble(a, high - 1);
}
T ( n ) = T ( n − 1 ) + n T(n)=T(n - 1) + n T(n)=T(n−1)+n , T ( 1 ) = c T(1)=c T(1)=c
如下展开过程
T ( n ) = T ( n − 2 ) + ( n − 1 ) + n T(n)=T(n - 2) + (n - 1) + n T(n)=T(n−2)+(n−1)+n
T ( n ) = T ( n − 3 ) + ( n − 1 ) + ( n − 2 ) + n T(n)=T(n - 3) + (n - 1) + (n - 2) + n T(n)=T(n−3)+(n−1)+(n−2)+n
⋯ \cdots ⋯
T ( n ) = T ( 1 ) + 2 + ⋯ + n = T ( 1 ) + ( n − 1 ) n + 2 2 = c + n 2 2 + n 2 − 1 T(n)=T(1)+2+\cdots+n=T(1)+(n - 1)\frac{n+2}{2}=c+\frac{n^2}{2}+\frac{n}{2}-1 T(n)=T(1)+2+⋯+n=T(1)+(n−1)2n+2=c+2n2+2n−1
时间复杂度: O ( n 2 ) O(n^2) O(n2)
推导公式网址
推导公式网址

多路递归
例 1-汉诺塔
public class HanoiTower{static LinkedList<Integer> a = new LinkedList<>();static LinkedList<Integer> b = new LinkedList<>();static LinkedList<Integer> c = new LinkedList<>();static void init(int n) {for (int i = n; i >= 1; i--) {a.addLast(i);}}// n 为圆盘个数// a, 源// b, 借// c, 目标static void move(int n, LinkedList<Integer> a, LinkedList<Integer> b, LinkedList<Integer> c) {if (n == 0) {return;}move(n - 1, a, c, b); // 借助c盘,将a盘的n-1个移到b盘c.addLast(a.removeLast()); // 将a盘中的最后一个移到c盘move(n - 1, b, a, c); // 借助a盘,将b盘的n-1个移动到c盘}public void print(){System.out.println("------------");System.out.println(a);System.out.println(b);System.out.println(c);}public static void main(String[] args) {// init(3);// print(); // a=[3, 2, 1], b=[], c=[]// b.addLast(a.removeLast()); // print(); // a=[3, 2], b=[1], c[]init(3);print();move(3, a, b, c);print();}
}
使用展开定理,或者使用公式网址,子问题个数是2,数据规模比原来减少1, T ( n ) = 2 T ( n − 1 ) + c T(n)=2T(n-1)+c T(n)=2T(n−1)+c ,中间操作(将a中的最后一个移动到c)看作常数 c c c 。

例 2-杨辉三角
public class PascalTriangle {// 返回某个位置的值public static int element(int i, int j) {if (i == 0 || i == j) {return 1;}return element(i - 1, j - 1) + element(i - 1, j);}// 打印空格public void printSpace(int n, int i) {int num = (n - 1 - i) * 2;for(int j = 0; j < num; j++) {System.out.print(" ");}}// 打印前n行的杨辉三角public static void print(int n) {for(int i = 0; i < n; i++) {printSpace(n, i);for(int j = 0; j <= i; j++) {System.out.printf("-%4d", element(i, j)); // 左对齐,并占4位}System.out.print(); // 换行处理}}public static void main(String[] args) {print(5);}}
改进杨辉三角,使用二维数组记录已经计算过的每项元素
public class PascalTriangle {// 返回某个位置的值public static int element(int[][] triangle, int i, int j) {if (triangle[i][j] > 0) {return triangle[i][j];}if (i == 0 || i == j) {triangle[i][j] = 1;return 1;}triangle[i][j] = element(triangle, i - 1, j - 1) + element(triangle, i - 1, j)return triangle[i][j];} // 打印前n行的杨辉三角public static void print(int n) {// 创建二维数组int[][] triangle = new int[n][];for(int i = 0; i < n; i++) {// 初始化每行i+1个元素triangle[i] = new int[i + 1];for(int j = 0; j <= i; j++) {System.out.printf("-%4d", element(triangle, i, j)); // 左对齐,并占4位}System.out.print(); // 换行处理}}public static void main(String[] args) {print(5);}}
改进杨辉三角,使用一维数组
public class PascalTriangle { public static void createRow(int[] row, int i) {if (i == 0) {row[0] = 1;return;}for(int j = i; j > 0; j--) {row[j] = row[j] + row[j - 1];}}// 打印前n行的杨辉三角public static void print(int n) {// 初始一维数组int[] triangle = new int[n];for(int i = 0; i < n; i++) {// 计算createRow(row, i);for(int j = 0; j <= i; j++) {System.out.printf("-%4d", element(triangle, i, j)); // 左对齐,并占4位}System.out.print(); // 换行处理}}public static void main(String[] args) {print(5);}}
相关文章:

递归--数据结构--黑马
递归 总结一句话,上手直接多刷Leetcode,比看这个更有用。 定义 递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集。 例如,单链表递归遍历的例子: void f(Node node) {if (node null) {retu…...

【3.1】贪心算法-解分发饼干
一、题目 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是, 每个孩子最多只能给一块饼干 。 对每个孩子i,都有一个 胃口值 g[i] ,这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干j,都有一个…...
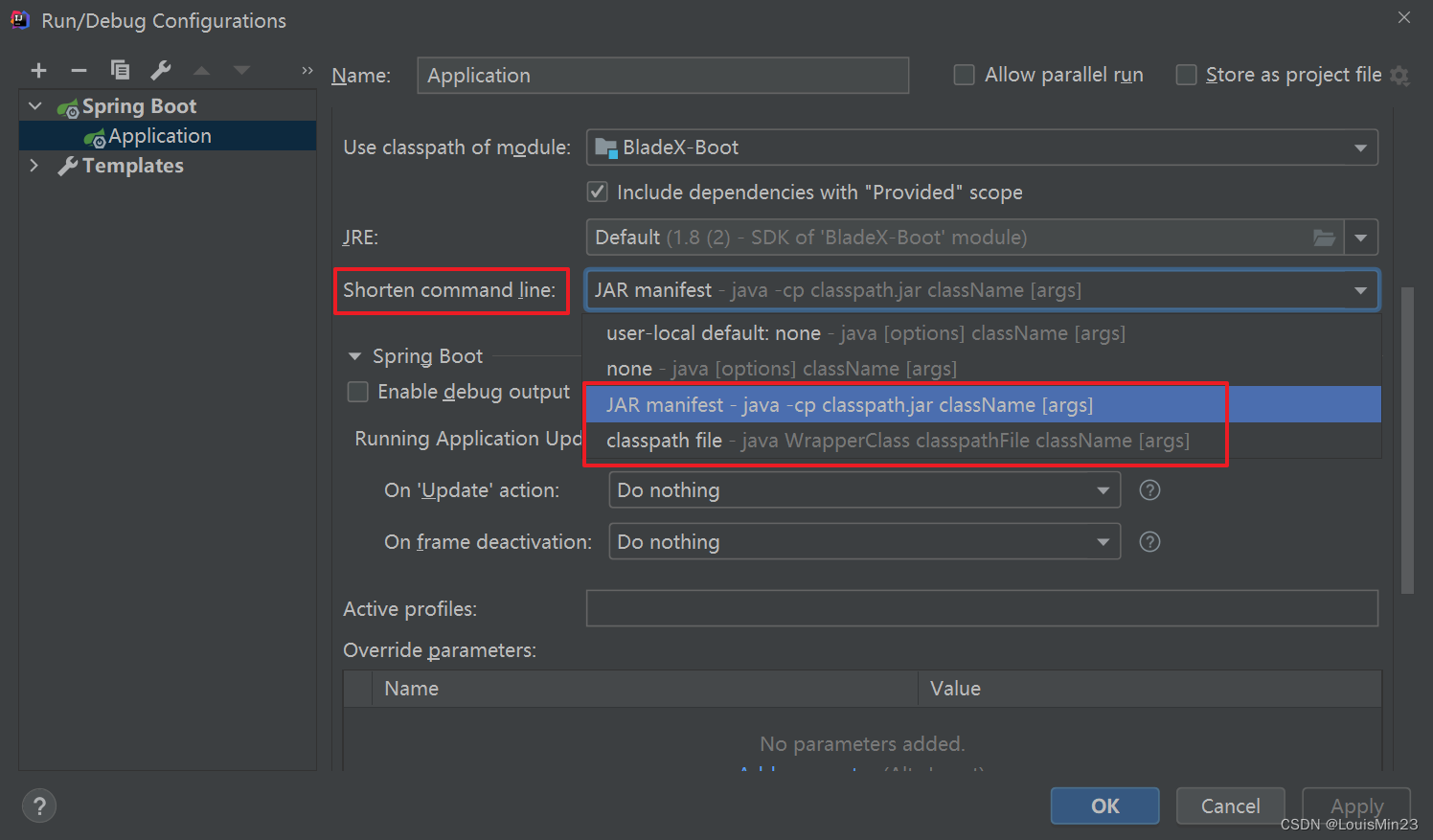
解决 Error running ‘Application‘: Command line is too long.
一、项目场景: 运行刚拉取下来的项目代码,出现下面问题描述的错误提示。 二、问题描述 Error running Application: Command line is too long. Shorten command line for Application or also for Spring Boot default configuration? 翻译翻译&…...

衡量与归因将是Netflix程序化广告业务的首要任务
作者:刀客doc 8月20日,Netflix宣布今年上半年,品牌的招商收入同比增长了150%,广告主来自旅游、汽车、零售商、快餐和大众快消等行业。这一消息提振了资本市场对Netflix广告业务的信心,8月20日收盘创下每股 698.54 美元…...

关于如何在已有qt项目中添加该项目的单元测试工程
关于如何在已有qt项目中添加该项目的单元测试工程 新建一个子目录工程,把已有项目作为子工程添加进去,然后新建单元测试工程也作为子工程添加进去。单元测试项目要独立于实际项目工程,确保去掉测试项目后,实际项目仍可以正常运行…...

深度剖析数字媒体产业链的无限潜力与创新生态
在当今信息爆炸的时代,数字媒体产业链正以势不可挡的姿态展现出其令人瞩目的无限潜力与创新生态。 数字媒体的发展潜力简直无可限量。从在线视频的爆发式增长,到虚拟现实和增强现实技术带来的沉浸式体验,再到社交媒体平台上丰富多彩的内容创…...

集团数字化转型方案(十二)
集团数字化转型方案致力于通过构建一个集成化的数字平台,全面应用大数据分析、人工智能、云计算和物联网等前沿技术,推动业务流程、管理模式和决策机制的全面升级。该方案将从业务流程的数字化改造开始,优化资源配置,提升运营效率…...

Andrid异步更新UI:Handler(二)深入了解:Message你真的会创建?它是如何子线程和主线程通知?
目录 为什么会有HandlerHandler的原理,以及对象讲解主线程的loop在哪里,为什么主线程loop没有阻塞呢?Looper如何保证唯一Handler为什么会引发内存泄漏呢?Message应该如何创建它? 一、为什么会有Handler 线程分为主线…...

2025计算机毕设50条小众好做的Java题目【计算机毕设选题推荐】
随着2025年的到来,计算机专业的学生们又迎来了毕业设计的关键时刻。对于大多数学生来说,选择一个合适的毕业设计题目往往是一项艰巨的任务。本文旨在为那些正在为毕业设计题目烦恼的同学们提供一些灵感和建议,特别是针对使用Java技术栈的同学…...

day06_算法训练
一. Stream流 1.1 Stream流概述 概念: jdk1.8以后提供的新的API, 主要用于批量操作数据(集合的另外一种操作方式),代码非常简洁 流式处理思想: 2.2 Stream对象获取 1.单列集合的Stream流对象获取 2.双列集合的Stream流对象获取 3.数组的Stream流对象获取 4.散装数据的St…...

@SpringBootTest单元测试中报错:无法自动装配,找不到 ‘XXX‘ 类型的 Bean
一开始照着网上教程讲Springboot原理中的代码来copy写的↓ import com.google.gson.Gson; import com.itheima.pojo.Result; import org.junit.jupiter.api.Test; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.boot.test.cont…...
简介、安装、配置、使用)
nodemon学习(一)简介、安装、配置、使用
nodemon用来监视node.js应用程序中的任何更改并自动重启服务,非常适合用在开发环境中。以前,我们开发一个node后端服务时,每次更改文件,均需重启一下,服务才能生效。这使我们的开发效率降低了很多。nodemon的出现,可以…...

【Qt从摄像头视频中获取数据】
有时候需要在视频上画图,所以需要能获取到每一帧视频数据。 以前从视频文件或视频流中得到帧,一般都是使用qt ffmpeg或qt vlc。 qt对显示处理视频大体有以下方法: QMediaPlayer QVideoWidget 这种方法只适合简单的显示视频功能ÿ…...
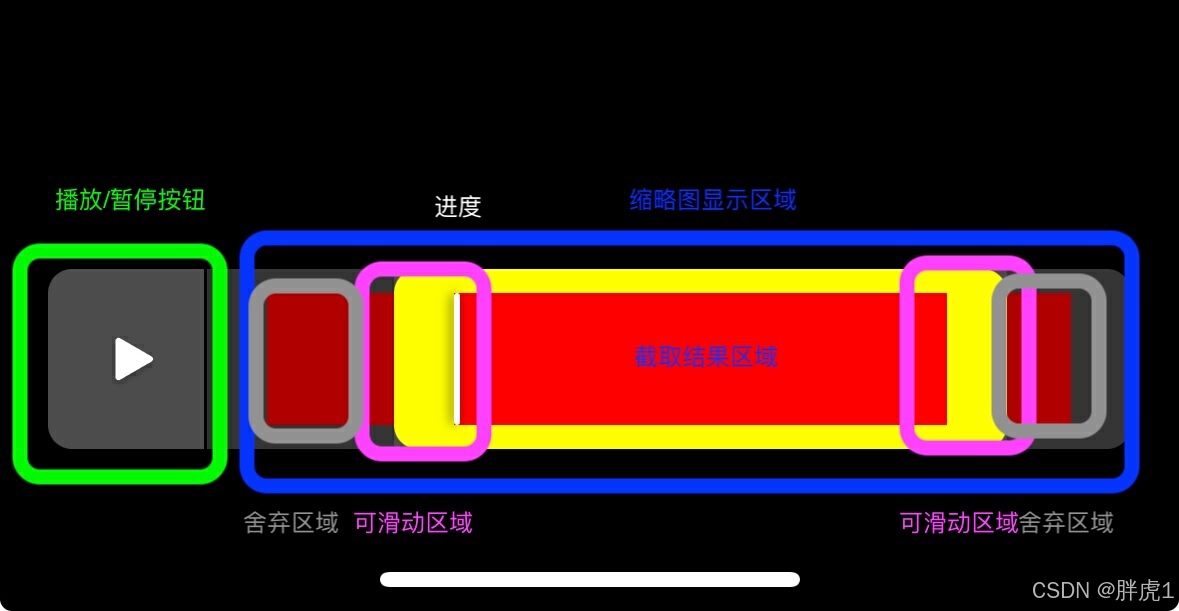
视频截取中的UI小组件
引言 视频截取在社交类 APP 中十分常见。有了上传视频的功能,就不可避免地需要提供截取和编辑的选项。如果我们过度依赖第三方库,项目的代码可能会变得异常臃肿,因为这些库往往包含许多我们用不到的功能,而且它们的 UI 样式和功能…...

java设计模式--结构型模式
结构性模式:适配器模式、桥接模式、装饰模式、组合模式、外观模式、享元模式、代理模式 适配器模式 适配器模式(Adapter Pattern) 充当两个不兼容接口之间的桥梁,属于结构型设计模式。目的是将一个类的接口转换为另一个接口&am…...

消息中间件:Kafka消息丢失与堆积问题分析与解决方案
消息中间件:Kafka消息丢失与堆积问题分析与解决方案 Kafka作为分布式消息系统,广泛应用于实时数据流处理、大数据分析等领域。然而,在实际应用中,Kafka可能会面临消息丢失和消息堆积的问题,这些问题如果得不到有效处理…...

mac终端代理配置指南
终端代理配置指南 在 macOS 中,你可以通过几种不同的方法来配置终端代理。这里介绍两种常见的设置方式:使用 alias 和 shell 函数。 方法 1:使用 Alias 配置代理 打开终端配置文件 默认情况下,macOS 终端使用的是 zsh。如果你的系…...

mbedTLS生成客户端,服务端密钥及CA证书
1. mbedTLS源码:https://github.com/Mbed-TLS/mbedtls.git 2. 生成步骤: 2.1 编译上述源码 2.2 生成CA私钥和自签名证书: 进入编译的build目录,比如:/mbedtls-development/build# 2.2.1生成CA私钥 执行下面的命令&…...

如何有效应对突发技术故障:以网易云音乐为例
引言 在互联网行业,任何一个在线服务都可能遭遇突发的技术故障。这些故障不仅影响用户体验,还可能对公司的品牌形象造成损害。因此,如何快速响应并高效解决这些问题成为了每一个开发团队的重要课题。本文将以网易云音乐在2024年8月19日下午遭…...

上传文件到github仓库
REF: https://blog.csdn.net/litianxiang_kaola/article/details/74075151 已有repository,往仓库里更新内容 点击gitlab里的clone 在git bash中使用git clone,这个时候会将网上的仓库下载到本地,你可以把想要更新的内容直接拖到仓库里 …...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
