Python数据结构与算法篇(五)-- 二分查找与二分答案
1 二分法介绍
1.1 定义
二分查找又称折半查找、二分搜索、折半搜索等,是一种在静态查找表中查找特定元素的算法。
所谓静态查找表,即只能对表内的元素做查找和读取操作,不允许插入或删除元素。
使用二分查找算法,必须保证查找表中存放的是有序序列(升序或者降序)。换句话说,存储无序序列的静态查找表,除非先对数据进行排序,否则不能使用二分查找算法。它针对的是一个有序的数据集合,查找思想有点类似分治思想。每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0。下图对比了顺序查找和二分查找的不同:

二分查找的最基本问题是在有序数组里查找一个特定的元素,还可以应用在:
- 在半有序(旋转有序或者是山脉)数组里查找元素;
- 确定一个有范围的整数;
- 需要查找的目标元素满足某个特定的性质。
二分查找算法的时间复杂度可以用 O(log2n)O(log_2n)O(log2n) 表示(nnn 为查找表中的元素数量,底数 2 可以省略)。和顺序查找算法的 O(n)O(n)O(n) 相比,显然二分查找算法的效率更高,且查找表中的元素越多,二分查找算法效率高的优势就越明显。
1.2 二分法的三种写法
1. 模板一
class Solution(object):def search(self, nums: List[int], target: int) -> int:# 特殊用例判断n = len(nums)if n == 0:return -1# 在 [left, right] 区间里查找targetleft, right = 0, n - 1while left <= right:# 为了防止 left + right 整形溢出,写成如下形式# Python 使用 BigInteger,所以不用担心溢出,但还是推荐使用如下方式mid = left + (right - left) // 2if nums[mid] == target:return midelif nums[mid] > target:# 下一轮搜索区间:[left, mid - 1]right = mid - 1else:# 此时:nums[mid] < target# 下一轮搜索区间:[mid + 1, right]left = mid + 1return -1
注意事项:
- 许多刚刚写的朋友,经常在写
left = mid + 1;还是写right = mid - 1; 感到困惑,一个行之有效的思考策略是:永远去想下一轮目标元素应该在哪个区间里:- 如果目标元素在区间
[left, mid - 1]里,就需要设置设置right = mid - 1; - 如果目标元素在区间
[mid + 1, right]里,就需要设置设置left = mid + 1;
- 如果目标元素在区间
考虑不仔细是初学二分法容易出错的地方,这里切忌跳步,需要仔细想清楚每一行代码的含义。
- 二分查找算法是典型的「减治思想」的应用,我们使用二分查找将待搜索的区间逐渐缩小,以达到「缩减问题规模」的目的;
- 循环可以继续的条件是
while (left <= right),特别地,当left == right即当待搜索区间里只有一个元素的时候,查找也必须进行下去; mid = (left + right) // 2;在left + right整形溢出的时候,mid 会变成负数,回避这个问题的办法是写成mid = left + (right - left) // 2。
2. 模板二
版本一:
def search(nums: List[int], left: int, right: int, target: int) -> int:while left < right:# 选择中位数时下取整mid = left + (right - left) // 2if check(mid):# 下一轮搜索区间是 [mid + 1, right]left = mid + 1else:# 下一轮搜索区间是 [left, mid]right = mid# 退出循环的时候,程序只剩下一个元素没有看到。# 视情况,是否需要单独判断 left(或者 right)这个下标的元素是否符合题意
版本二:
def search(nums: List[int], left: int, right: int, target: int) -> int:while left < right:# 选择中位数时上取整mid = left + (right - left + 1) // 2if check(mid):# 下一轮搜索区间是 [left, mid - 1]right = mid - 1else:# 下一轮搜索区间是 [mid, right]left = mid# 退出循环的时候,程序只剩下一个元素没有看到。# 视情况,是否需要单独判断 left(或者 right)这个下标的元素是否符合题意
理解模板代码的要点:
- 核心思想:虽然模板有两个,但是核心思想只有一个,那就是:把待搜索的目标元素放在最后判断,每一次循环排除掉不存在目标元素的区间,目的依然是确定下一轮搜索的区间;
- 特征:
while (left < right):,这里使用严格小于<表示的临界条件是:当区间里的元素只有 2 个时,依然可以执行循环体。换句话说,退出循环的时候一定有left == right成立,这一点在定位元素下标的时候极其有用; - 在循环体中,先考虑
nums[mid]在满足什么条件下不是目标元素,进而考虑两个区间[left, mid - 1]以及[mid + 1, right]里元素的性质,目的依然是确定下一轮搜索的区间; 注意 1: 先考虑什么时候不是解,是一个经验,在绝大多数情况下不易出错,重点还是确定下一轮搜索的区间,由于这一步不容易出错,它的反面(也就是else语句的部分),就不用去考虑对应的区间是什么,直接从上一个分支的反面区间得到,进而确定边界如何设置; - 根据边界情况,看取中间数的时候是否需要上取整; 注意 2: 这一步也依然是根据经验,建议先不要记住结论,在使用这个思想解决问题的过程中,去思考可能产生死循环的原因,进而理解什么时候需要在括号里加 1 ,什么时候不需要;
- 在退出循环以后,根据情况看是否需要对下标为
left或者right的元素进行单独判断,这一步叫「后处理」。在有些问题中,排除掉所有不符合要求的元素以后,剩下的那 1 个元素就一定是目标元素。如果根据问题的场景,目标元素一定在搜索区间里,那么退出循环以后,可以直接返回 left(或者 right)。
以上是这两个模板写法的所有要点,并且是高度概括的。请读者一定先抓住这个模板的核心思想,在具体使用的过程中,不断地去体会这个模板使用的细节和好处。只要把中间最难理解的部分吃透,几乎所有的二分问题就都可以使用这个模板来解决,因为「减治思想」是通用的。好处在这一小节的开篇介绍过了,需要考虑的细节最少。
学习建议:一定需要多做练习,体会这(两)个模板的使用。
注意事项:
- 先写分支,再决定中间数是否上取整;
- 在使用多了以后,就很容易记住,只要看到 left = mid ,它对应的取中位数的取法一定是
mid = left + (right - left + 1) // 2。
3. 模板三
def search(nums: List[int], left: int, right: int, target: int) -> int:while left + 1 < right:# 选择中位数时下取整mid = left + (right - left) // 2if nums[mid] == target:return midelif nums[mid] < target:left = midelse:right = midif nums[left] == target:return leftif nums[right] == target:return rightreturn -1
- 这一版代码和模板二没有本质区别,一个显著的标志是:循环可以继续的条件是
while (left + 1 < right):,这说明在退出循环的时候,一定有left + 1 == right成立,也就是退出循环以后,区间有 2 个元素,即[left, right]; - 这种写法的优点是:不用理解上一个版本在分支出现 left = mid 的时候中间数上取整的行为;
- 缺点是显而易见的:
while (left + 1 < right):写法相对于while (left < right):和while (left <= right):来说并不自然;- 由于退出循环以后,区间一定有两个元素,需要思考哪一个元素才是需要找的,即「后处理」一定要做,有些时候还会有先考虑
left还是right的区别。
小结:
- 模板一:最好理解的版本,但是在刷题的过程中,需要处理一些边界的问题,一不小心容易出错;
- 模板二:强烈推荐掌握的版本,应先理解思想,再通过实际应用去体会这个模板的细节,熟练使用以后就会觉得非常自然;
- 模板三:可以认为是模板二的避免踩坑版本,只要深刻理解了模板二,模板三就不在话下。
实际应用中,选择最好理解的版本即可。
这里有一个提示:模板二考虑的细节最少,可以用于解决一些相对复杂的问题。缺点是:学习成本较高,初学的时候比较容易陷入死循环,建议大家通过多多使用,并且尝试 debug,找到死循环的原因,进而掌握。
题解核心内容:所有模板都一样,不可以套模板,而应该仔细看题(解题的关键在认真读题),分析清楚题目要找的答案需要满足什么性质。采用两边夹的方式,每一轮把待搜索区间分成两个部分,排除掉一定不是答案的区间,最后左右指针重合的地方就是我们要找的元素。一定要分析清楚题目的意思,分析清楚要找的答案需要满足什么性质。应该清楚模板具体的用法,明白需要根据题意灵活处理、需要变通的地方,不可以认为每一行代码都是模板规定死的写法,不可以盲目套用、死记硬背。
2 常见题型
2.1 二分求下标(在数组中查找符合条件的元素的下标)
题库列表
| 题号 | 链接 |
|---|---|
| 704 | 二分查找(简单) |
| 35 | 搜索插入位置(简单) |
| 300 | 最长上升子序列(中等) |
| 34 | 在排序数组中查找元素的第一个和最后一个位置(简单) |
| 611 | 有效三角形的个数 |
| 436 | 寻找右区间(中等) |
| 4 | 寻找两个有序数组的中位数(困难) |
2.2 完全有序
704. 二分查找
题目描述:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
# lower_bound 返回最小的满足 nums[i] >= target 的 i
# 如果数组为空,或者所有数都 < target,则返回 len(nums)
# 要求 nums 是非递减的,即 nums[i] <= nums[i + 1]# 闭区间写法
def lower_bound(nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1 # 闭区间 [left, right]while left <= right: # 区间不为空# 循环不变量:# nums[left-1] < target# nums[right+1] >= targetmid = (left + right) // 2if nums[mid] < target:left = mid + 1 # 范围缩小到 [mid+1, right]else:right = mid - 1 # 范围缩小到 [left, mid-1]return left # 或者 right+1# 左闭右开区间写法
def lower_bound2(nums: List[int], target: int) -> int:left, right = 0, len(nums) # 左闭右开区间 [left, right)while left < right: # 区间不为空# 循环不变量:# nums[left-1] < target# nums[right] >= targetmid = (left + right) // 2if nums[mid] < target:left = mid + 1 # 范围缩小到 [mid+1, right)else:right = mid # 范围缩小到 [left, mid)return left # 或者 right# 开区间写法
def lower_bound3(nums: List[int], target: int) -> int:left, right = -1, len(nums) # 开区间 (left, right)while left + 1 < right: # 区间不为空mid = (left + right) // 2# 循环不变量:# nums[left] < target# nums[right] >= targetif nums[mid] < target:left = mid # 范围缩小到 (mid, right)else:right = mid # 范围缩小到 (left, mid)return right # 或者 left+1class Solution:def search(self, nums: List[int], target: int) -> int:i = lower_bound(nums, target) # 选择其中一种写法即可return i if i < len(nums) and nums[i] == target else -1

35. 搜索插入位置
题目描述:给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
class Solution:def searchInsert(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1while left <= right:mid = (left + right) // 2if nums[mid] == target:return midelif nums[mid] < target:left = mid + 1else:right = mid - 1return left

class Solution:def searchInsert(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) # 采用左闭右开区间[left,right)while left < right: # 右开所以不能有=,区间不存在mid = left + (right - left)//2 # 防止溢出, //表示整除if nums[mid] < target: # 中点小于目标值,在右侧,可以得到相等位置left = mid + 1 # 左闭, 所以要+1else:right = mid # 右开, 真正右端点为mid-1return left # 此算法结束时保证left = right, 返回谁都一样
300. 最长上升子序列
题目描述:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
1. 动态规划 + 二分查找
# Dynamic programming + Dichotomy.
class Solution:def lengthOfLIS(self, nums: [int]) -> int:tails, res = [0] * len(nums), 0for num in nums:i, j = 0, reswhile i < j:m = (i + j) // 2if tails[m] < num: i = m + 1 # 如果要求非严格递增,将此行 '<' 改为 '<=' 即可。else: j = mtails[i] = numif j == res: res += 1return res

2. 动态规划
class Solution:def lengthOfLIS(self, nums: List[int]) -> int:if not nums: return 0dp = [1] * len(nums)for i in range(len(nums)):for j in range(i):if nums[j] < nums[i]: # 如果要求非严格递增,将此行 '<' 改为 '<=' 即可。dp[i] = max(dp[i], dp[j] + 1)return max(dp)

34. 在排序数组中查找元素的第一个和最后一个位置
题目描述:给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target,返回 [-1, -1]。
class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:if not nums or target not in nums: # 特例,二分查找失败return [-1, -1]return [self.lower_bound(nums, target), self.upper_bound(nums, target)]def upper_bound(self, nums: List[int], target: int): # 寻找上边界left, right = 0, len(nums)-1while left <= right:mid = left + (right - left) // 2if nums[mid] <= target: # 移动左指针left = mid + 1else: # 移动右指针right = mid -1return rightdef lower_bound(self, nums: List[int], target: int): # 寻找下边界left, right = 0, len(nums)-1while left <= right:mid = left + (right - left) // 2if nums[mid] >= target: # 当nums[mid]大于等于目标值时,继续在左区间检索,找到第一个数right = mid - 1else: # nums[mid]小于目标值时,则在右区间继续检索,找到第一个等于目标值的数left = mid + 1return left

611. 有效三角形的个数
题目描述:给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。
将数组 nums 进行升序排序,随后使用二重循环枚举 a 和 b。设 a=nums[i],b=nums[j]a=nums[i], b=nums[j]a=nums[i],b=nums[j],为了防止重复统计答案,我们需要保证 i<ji<ji<j。剩余的边 c 需要满足 c<nums[i]+nums[j]c<nums[i]+nums[j]c<nums[i]+nums[j],我们可以在 [j+1,n−1][j+1,n−1][j+1,n−1] 的下标范围内使用二分查找(其中 nnn 是数组 nums 的长度),找出最大的满足 nums[k]<nums[i]+nums[j]nums[k]<nums[i]+nums[j]nums[k]<nums[i]+nums[j] 的下标 kkk,这样一来,在 [j+1,k][j+1, k][j+1,k] 范围内的下标都可以作为边 ccc 的下标,我们将该范围的长度 k−jk−jk−j 累加入答案。

1. 排序+二分查找
class Solution:def triangleNumber(self, nums: List[int]) -> int:nums.sort()length = len(nums)ans = 0for i in range(length):for j in range(i+1, length):left, right = j+1, length while left < right: # 找边界,mid = (left + right)//2if nums[mid] < nums[i] + nums[j]:left = mid + 1else:right = midans += left - 1 - jreturn ans
2. 排序+双指针
我们将当 a=nums[i],b=nums[j]a=nums[i], b=nums[j]a=nums[i],b=nums[j] 时,最大的满足 nums[k]<nums[i]+nums[j]nums[k]<nums[i]+nums[j]nums[k]<nums[i]+nums[j] 的下标 kkk 记为 ki,jk_{i,j}ki,j。可以发现,如果我们固定 iii,那么随着 jjj 的递增,不等式右侧 nums[i]+nums[j]nums[i]+nums[j]nums[i]+nums[j] 也是递增的,因此 ki,jk_{i,j}ki,j 也是递增的。
这样一来,我们就可以将 jjj 和 kkk 看成两个同向(递增)移动的指针,将方法一进行如下的优化:
- 我们使用一重循环枚举 iii。当 iii 固定时,我们使用双指针同时维护 jjj 和 kkk,它们的初始值均为 iii;
- 我们每一次将 jjj 向右移动一个位置,即 j←j+1j←j+1j←j+1,并尝试不断向右移动 kkk,使得 kkk 是最大的满足 nums[k]<nums[i]+nums[j]nums[k]<nums[i]+nums[j]nums[k]<nums[i]+nums[j] 的下标。我们将 max(k−j,0)max(k−j, 0)max(k−j,0) 累加入答案。
class Solution:def triangleNumber(self, nums: List[int]) -> int:nums.sort()length = len(nums)ans = 0for i in range(length):k = i + 1 for j in range(i+1, length):while k+1 < length and nums[i] + nums[j] > nums[k+1]:k += 1ans += max(k-j, 0)return ans
436. 寻找右区间
题目描述:


class Solution:def findRightInterval(self, intervals: List[List[int]]) -> List[int]:start_map = {interval[0] : i for i, interval in enumerate(intervals)} # 以区间左侧构建索引字典starts = [interval[0] for interval in intervals] # 取出区间的左侧res = []starts.sort()for interval in intervals:pos = self.higher_find(starts, interval[1]) # 遍历每个区间的右侧,在所有区间的左侧进行二分查找res.append(start_map[starts[pos]] if pos != -1 else -1)return resdef higher_find(self, nums, target):left, right = 0, len(nums) # 左闭右开while left < right:mid = left + (right - left) // 2if nums[mid] >= target:right = midelse:left = mid + 1if left < len(nums) and nums[left] >= target: # 最后判断一下,是否满足条件return leftreturn -1

4. 寻找两个正序数组的中位数
题目描述:给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。算法的时间复杂度应该为 O(log(m+n))O(log (m+n))O(log(m+n))。
class Solution:def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:def getKthElement(k):"""- 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较- 这里的 "/" 表示整除- nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个- nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个- 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个- 这样 pivot 本身最大也只能是第 k-1 小的元素- 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组- 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组- 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数"""index1, index2 = 0, 0while True:# 特殊情况if index1 == m:return nums2[index2 + k - 1]if index2 == n:return nums1[index1 + k - 1]if k == 1:return min(nums1[index1], nums2[index2])# 正常情况newIndex1 = min(index1 + k // 2 - 1, m - 1)newIndex2 = min(index2 + k // 2 - 1, n - 1)pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2]if pivot1 <= pivot2:k -= newIndex1 - index1 + 1index1 = newIndex1 + 1else:k -= newIndex2 - index2 + 1index2 = newIndex2 + 1m, n = len(nums1), len(nums2)totalLength = m + nif totalLength % 2 == 1:return getKthElement((totalLength + 1) // 2)else:return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) / 2

2.3 不完全有序
题库列表:
| 题号 | 链接 |
|---|---|
| 33 | 搜索旋转排序数组(中等) |
| 81 | 搜索旋转排序数组 II(中等) |
| 153 | 寻找旋转排序数组中的最小值(中等) |
| 154 | 寻找旋转排序数组中的最小值 II(困难) |
| 852 | 山脉数组的峰顶索引(简单) |
| 1095 | 山脉数组中查找目标值(中等) |
33. 搜索旋转排序数组
题目描述:整数数组 nums 按升序排列,数组中的值 互不相同。在传递给函数之前,nums 在预先未知的某个下标 k(0<=k<nums.length)k(0 <= k < nums.length)k(0<=k<nums.length) 上进行了旋转,使数组变为 [nums[k],nums[k+1],...,nums[n−1],nums[0],nums[1],...,nums[k−1]][nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]][nums[k],nums[k+1],...,nums[n−1],nums[0],nums[1],...,nums[k−1]](下标从0开始计数)。例如,[0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。给你旋转后的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1。
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums)-1while left <= right:mid = (left + right) // 2if nums[mid] == target:return midif nums[mid] >= nums[left]: # 左半部分有序if nums[0] <= target < nums[mid]: # target 在左半部分right = mid - 1else:left = mid + 1else: # 右半部分有序if nums[mid] < target <= nums[len(nums)-1]: # target 在右半部分left = mid + 1else:right = mid - 1return -1

81. 搜索旋转排序数组 II
题目描述:

class Solution:def search(self, nums: List[int], target: int) -> bool:left, right = 0, len(nums)-1while left <= right:mid = (left + right)//2if nums[mid] == target:return Trueif nums[mid] == nums[left]: # 去重left += 1continueif nums[left] <= nums[mid]: # 左半部分有序,在左侧二分查找if nums[left] <= target < nums[mid]:right = mid - 1else:left = mid + 1else: # 右半部分有序,在右侧二分查找if nums[mid] < target <= nums[right]:left = mid + 1else:right = mid - 1return False
153. 寻找旋转排序数组中的最小值
题目描述:



class Solution:def findMin(self, nums: List[int]) -> int: low, high = 0, len(nums) - 1while low < high:pivot = low + (high - low) // 2if nums[pivot] < nums[high]:high = pivot else:low = pivot + 1return nums[low]
154. 寻找旋转排序数组中的最小值 II
题目描述:

class Solution:def findMin(self, nums: List[int]) -> int:left, right = 0, len(nums)-1while left < right:mid = (left+right) // 2if nums[mid] < nums[right]:right = midelif nums[mid] > nums[right]:left = mid + 1else:right -= 1 # 去重return nums[left]

852. 山脉数组的峰顶索引(简单)
题目描述:

1. 顺序查找
class Solution:def peakIndexInMountainArray(self, arr: List[int]) -> int:# 顺序查找最大值for i in range(1, len(arr) - 1):if arr[i] > arr[i + 1]:return i
2. 二分查找
class Solution:def peakIndexInMountainArray(self, arr: List[int]) -> int:# 二分查找最大值left, right = 0, len(arr) - 1while left < right:mid = (left + right) // 2if arr[mid] > arr[mid + 1]:right = midelse:left = mid + 1return left
1095. 山脉数组中查找目标值
题目描述:

class Solution:def findInMountainArray(self, target: int, mountain_arr: 'MountainArray') -> int:'''先使用二分法找到数组的峰值。在峰值左边使用二分法寻找目标值。如果峰值左边没有目标值,那么使用二分法在峰值右边寻找目标值。'''head, tail = 0, mountain_arr.length()-1while head < tail: # 找峰值,注意越界处理mid = (head+tail)//2if mountain_arr.get(mid) < mountain_arr.get(mid+1):head = mid + 1else:tail = midpeak = headans = self.binarySearch(mountain_arr, target, 0, peak) # 在左半边搜索if ans != -1:return ansreturn self.binarySearch(mountain_arr, target, peak+1, mountain_arr.length()-1, lambda x:-x) # 在右半边搜索def binarySearch(self, mountain, target, left, right, key=lambda x: x): target = key(target) # 这里的key相当于把两边全部转为升序部分,也可以用target*reverse,根据reverse的正负来判断while left <= right:mid = (left + right) // 2curr = key(mountain.get(mid))if curr == target:return midelif curr < target:left = mid + 1else:right = mid - 1return -1
2.4 二分答案(在一个有范围的区间里搜索一个整数)
如果题目要我们找一个整数,这个整数有确定的范围,可以通过二分查找逐渐缩小范围,最后逼近到一个数。
定位一个有范围的整数,这件事情也叫「二分答案」或者叫「二分结果」。如果题目要求的是一个整数,这个整数有明确的范围,可以考虑使用二分查找。
| 题号 | 链接 |
|---|---|
| 69 | x 的平方根(简单) |
| 287 | 寻找重复数(中等) |
| 374 | 猜数字大小(简单) |
69. x 的平方根
题目描述:给你一个非负整数 x ,计算并返回 x 的算术平方根。由于返回类型是整数,结果只保留整数部分 ,小数部分将被舍去 。
class Solution:def mySqrt(self, x: int) -> int:left, right= 0, x//2while left <= right:mid = (left + right) // 2if mid * mid == x:return midif mid * mid < x:left = mid + 1else:right = mid - 1return left if left ** 2 <= x else left-1
287. 寻找重复数
题目描述:给定一个包含 n+1n+1n+1 个整数的数组 nums ,其数字都在 [1,n][1, n][1,n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。假设 nums 只有 一个重复的整数 ,返回 这个重复的数。你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1)O(1)O(1) 的额外空间。
1. 二分法
设数组长度为nnn,则数组中元素 ∈[1,n−1]\in[1, n-1]∈[1,n−1],且只有一个重复元素。一个直观的想法,设一个数字 k∈[1,n−1]k\in[1,n-1]k∈[1,n−1],统计数组中小于等于 kkk 的数字的个数 count:
- 若 count<=kcount<=kcount<=k,说明重复数字一定在 (k,n−1](k,n−1](k,n−1] 的范围内。
- 若 count>kcount>kcount>k,说明重复数字一定在 [0,k][0,k][0,k] 的范围内。
利用这个性质,我们使用二分查找逐渐缩小重复数字所在的范围。
- 初试化左右 数字 边界 left=1,right=n−1left=1, right=n-1left=1,right=n−1
- 循环条件 left<right:left<right:left<right:
- mid=(left+right)//2mid=(left+right)//2mid=(left+right)//2
- 按照性质,统计数组中小于等于 midmidmid 的元素个数 countcountcount
- 若 count<=midcount<=midcount<=mid,说明重复数字一定在 (mid,right](mid,right](mid,right] 的范围内。令 left=mid+1left=mid+1left=mid+1
- 若 count>midcount>midcount>mid,说明重复数字一定在 [left,mid][left,mid][left,mid] 的范围内。令 right=midright=midright=mid。
- 返回 leftleftleft
class Solution:def findDuplicate(self, nums: List[int]) -> int:left = 1right = len(nums) - 1while(left<right):mid=(left+right)//2count=0for num in nums:if(num<=mid):count+=1if(count<=mid):left=mid+1else:right=midreturn left
2. 快慢指针
分为两步:
- 找到环
- 找到环的入口(即重复元素)
找环:
- 定义快慢指针 slow=0,fast=0slow=0, fast=0slow=0,fast=0
- 进入循环:
- slowslowslow 每次走一步,即 slow=nums[slow]slow=nums[slow]slow=nums[slow]
- fastfastfast 每次走两步,即 fast=nums[nums[fast]]fast=nums[nums[fast]]fast=nums[nums[fast]]
- 当 slow==fastslow==fastslow==fast时,退出循环。 当快慢指针相遇时,一定在环内。此时假设slow 走了 kkk 步,则 fast 走了 2k2k2k 步。设环的周长为 ccc,则 kk%c==0k。
找环的入口: - 定义新的指针 find=0find=0find=0
- 进入循环:
- find 每次走一步,即 find=nums[find]find=nums[find]find=nums[find]
- slow每次走一步,即 slow=nums[slow]slow=nums[slow]slow=nums[slow]
- 当两指针相遇时,即 find==slowfind==slowfind==slow,返回 find
为何相遇时,找到的就是入口: 假设起点到环的入口(重复元素),需要 mmm 步。此时 slow 走了 n+mn+mn+m 步,其中 nnn 是环的周长 ccc 的整数倍,所以相当于 slow走了 mmm 步到达入口,再走了 nnn 步。所以相遇时一定是环的入口。
class Solution:def findDuplicate(self, nums: List[int]) -> int:slow=0fast=0while(1):slow=nums[slow]fast=nums[nums[fast]]if(slow==fast):breakfind=0while(1):find=nums[find]slow=nums[slow]if(find==slow):return find
374. 猜数字大小
题目描述:

# The guess API is already defined for you.
# @param num, your guess
# @return -1 if num is higher than the picked number
# 1 if num is lower than the picked number
# otherwise return 0
# def guess(num: int) -> int:class Solution:def guessNumber(self, n: int) -> int:left, right = 0, nwhile left <= right:mid = left + ((right-left)>>1)temp = guess(mid)if temp == 0:return midelif temp == 1:left = mid + 1else:right = mid -1
小结

二分法暂时告一段落,后面在学习中持续补充,谢谢大家的鼓励和支持!

参考
- 二分查找算法:https://ojeveryday.github.io/AlgoWiki/#/BinarySearch/README
- 二分算法:https://oi-wiki.org/basic/binary/
- 二分查找:https://www.cnblogs.com/jasonbourne3/p/17141780.html
- 算法与数据结构(七):二分查找法总结:https://blog.csdn.net/Dby_freedom/article/details/94332149
- 一文带你搞定二分查找及其多个变种:https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/solution/
- 写对二分查找不是套模板并往里面填空,需要仔细分析题意:https://leetcode.cn/problems/search-insert-position/solutions/10969/te-bie-hao-yong-de-er-fen-cha-fa-fa-mo-ban-python-/
- 二分查找(折半查找)算法详解:http://data.biancheng.net/view/336.html
相关文章:

Python数据结构与算法篇(五)-- 二分查找与二分答案
1 二分法介绍 1.1 定义 二分查找又称折半查找、二分搜索、折半搜索等,是一种在静态查找表中查找特定元素的算法。 所谓静态查找表,即只能对表内的元素做查找和读取操作,不允许插入或删除元素。 使用二分查找算法,必须保证查找表中…...
小游戏也要讲信用
当下,小游戏鱼龙混杂,官方为能更好地保护用户、开发者以及平台的权益,近日宣布7月1日起试行小游戏主体信用分机制。 主体信用分是什么呢?简单来说,这是针对小游戏主体下所有小游戏帐号行为,对开发者进行评…...

贪心算法11
1. 贪心算法的概念 所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。 贪心算法没有固定的算法框架,算法设计的关键是贪心…...
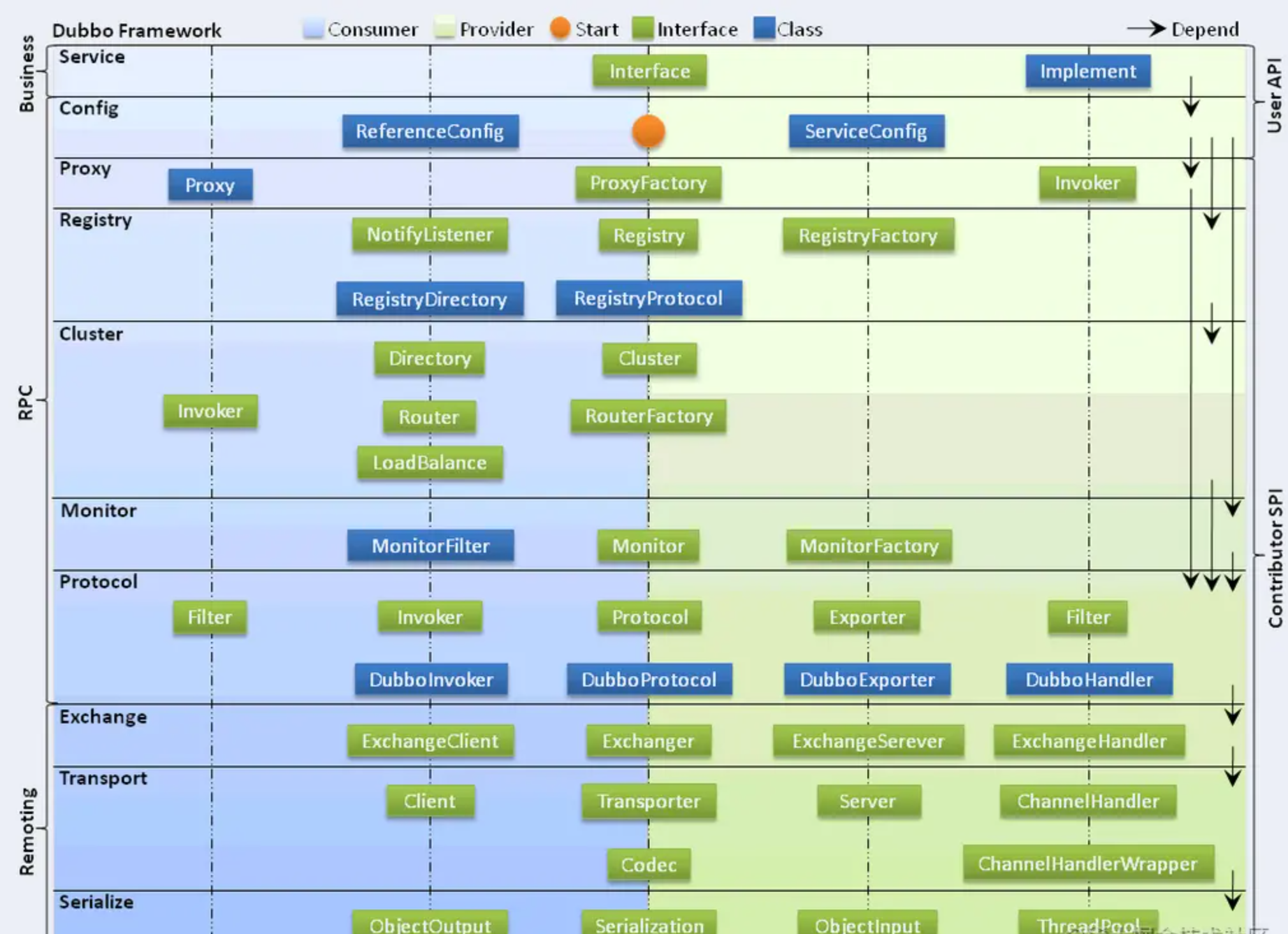
【并发编程】JUC并发编程(彻底搞懂JUC)
文章目录一、背景二、什么是JUC?三、JUC框架结构四、JUC框架概述五、JUC中常用类汇总六、相关名词进程和线程进程线程创建线程的几种常见的方式并发和并行用户线程和守护线程七、synchronized 作用范围:八、Lock锁(重点)什么是 Lock锁类型Lock接口lock()…...

Compose 动画 (七) : 高可定制性的动画 Animatable
1. Animatable和animateDpAsState的区别是什么 Animatable是Android Compose动画的底层API,如果我们查看源码,可以发现animateDpAsState内部是调用的animateValueAsState,而animateValueAsState内部调用的是Animatable animateDpAsState比A…...

vue3组件传值
1.父向子传值 父组件 引入子组件 import Son from ./components/Son.vue 设置响应式数据 const num ref(99) 绑定到子组件 <Son :num"num"></Son> 子组件 引入defineProps import { defineProps } from vue; 生成实例接收数据 type设置接收类…...

小白开发微信小程序00--文章目录
一个小白,一个老牛,空手能不能套白羊,能不能白嫖?我告诉你,一切都so easy,这个系列从0到106,屌到上天,盖过任何一个,试问,网上讲微信小程序开发的,…...
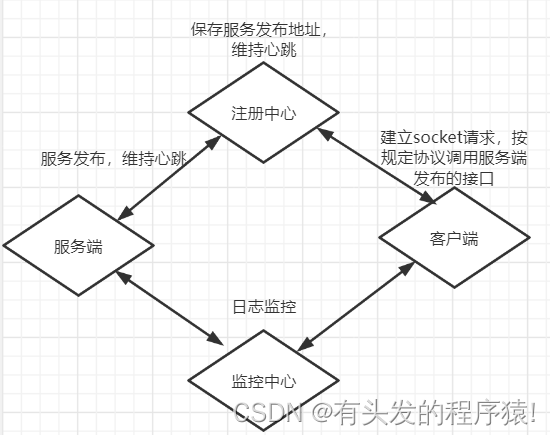
随手记录第九话 -- Java框架整合篇
框架莫过于Spring了,那就以它为起点吧。 本文只为整理复习用,详细内容自行翻看以前文章。 1.Spring 有人说是Spring成就Java,其实也不是并无道理。 1.1 Spring之IOC控制反转 以XML注入bean的方式为入口,定位、加载、注册&…...
电影《铃芽之旅》观后感
这周看了电影《铃芽之旅》,整部电影是新海诚的新作。电影讲述的是女主铃芽为了关闭往门,在日本旅行中,遭遇灾难的故事。 (1)往昔记忆-往昔之物 电影中,有很多的“往门”,换成中国的话说…...
Web自动化测试(二)(全网最给力自动化教程)
欢迎您来阅读和练手!您将会从本章的详细讲解中,获取很大的收获!开始学习吧! 2.4 CSS定位2.5 SeleniumBuilder辅助定位元素2.6 操作元素(键盘和鼠标事件) 正文 2.4 CSS定位 前言 大部分人在使用selenium定…...

【C语言经典例题!】逆序字符串
目录 一、题目要求 二、解题步骤 ①递归解法 思路 完整代码 ②循环解法 思路 完整代码 嗨大家好! 本篇博客中的这道例题,是我自己在一次考试中写错的一道题 这篇博客包含了这道题的几种解法,以及一些我自己对这道题的看法ÿ…...

21 - 二叉树(三)
文章目录1. 二叉树的镜像2. 判断是不是完全二叉树3. 完全二叉树的节点个数4. 判断是不是平衡二叉树1. 二叉树的镜像 #include <ctime> class Solution {public:TreeNode* Mirror(TreeNode* pRoot) {// write code hereif (pRoot nullptr) return pRoot;//这里记得要记得…...

【A-Star算法】【学习笔记】【附GitHub一个示例代码】
文章目录一、算法简介二、应用场景三、示例代码Reference本文暂学习四方向搜索,一、算法简介 一个比较经典的路径规划的算法 相关路径搜索算法: 广度优先遍历(BFC)深度优先遍历(DFC)Di jkstra算法&#…...

纽扣电池澳大利亚认证的更新要求
澳大利亚强制性安全和信息标准草案具体规定了对含有纽扣电池和纽扣电池以 及纽扣电池和纽扣电池本身的消费品的要求, 适用范围 1.本法规适用于: 纽扣锂电池(任何尺寸和类型); 直径为16毫米或以上的纽扣锂电池: 一起提供的纽扣电池(未预先安装在产品中)。 2.但是&…...

零代码零距离,明道云开放日北京站圆满结束
文/麦壁瑜 编辑/李雨珂 2023年3月17日,为期一天的明道云开放日北京站圆满结束。本次开放日迎来超过100名伙伴和客户现场参会,其中不乏安利、通用技术集团、民生银行、迈外迪、DELSK集团、中国人民养老保险、北京汽车等知名企业代表。北京大兴机场、作业…...
第五章Vue路由
文章目录相关理解vue-router的理解对SPA应用的理解路由的理解基本路由几个注意点嵌套路由——多级路由路由query参数命名路由路由的params参数路由的props配置路由跳转的replace方法编程式路由导航缓存路由组件路由组件独有的生命钩子activated和deactivated路由守卫全局路由守…...
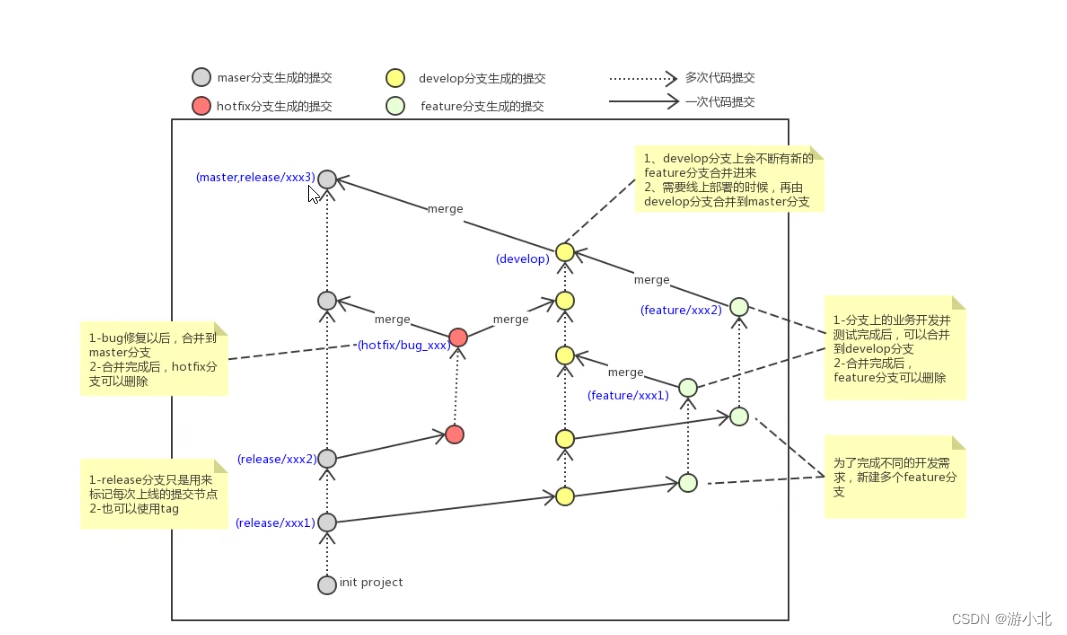
Git常用指令
Git是什么: Git是分布式版本控制系统(Distributed Version Control System,简称 DVCS),分为两种类型的仓库: 本地仓库和远程仓库 第一步先新建仓库,本地 init ,然后提交分枝 链接仓库…...

Java每日一练(20230329)
目录 1. 环形链表 II 🌟🌟 2. 基础语句 ※ 3. 最小覆盖子串 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 1. 环形…...
【面试题】JS的一些优雅写法 reduce和map
大厂面试题分享 面试题库 前后端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 web前端面试题库 VS java后端面试题库大全 JS的一些优雅写法 reduce 1、可以使用 reduce 方法来实现对象数组中根据某一key值求和 …...
)
【蓝桥杯真题】包子凑数(裴蜀定理、动态规划、背包问题)
题意 小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。 每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
