蚁群算法优化旅行问题
%%%%%%%%%%%%蚁群算法解决 TSP 问题%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
m = 50; %蚂蚁个数
Alpha = 1; %信息素重要程度参数
Beta = 5; %启发式因子重要程度参数
Rho = 0.1; %信息素蒸发系数
G = 200; %最大迭代次数
Q = 100; %信息素增加强度系数
C = [1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
3238 1229;4196 1044;4312 790;4386 570;3007 1970;2562 1756;...
2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;...
3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
2370 2975]; %31 个省会城市坐标
%%%%%%%%%%%%%%%第一步:变量初始化%%%%%%%%%%%%%%
n = size(C,1); %n 表示问题的规模(城市个数)
D = zeros(n,n); %D 表示两个城市距离间隔矩阵
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = ((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
else
D(i,j) = eps;
end
D(j,i) = D(i,j);
end
end
Eta = 1./D; %Eta 为启发因子,这里设为距离的倒数
Tau = ones(n,n); %Tau 为信息素矩阵
Tabu = zeros(m,n); %存储并记录路径的生成
NC = 1; %迭代计数器
R_best = zeros(G,n); %各代最佳路线
L_best = inf.*ones(G,1); %各代最佳路线的长度
figure(1); %优化解
while NC <= G
%%%%%%%%%%第二步:将 m 只蚂蚁放到 n 个城市上%%%%%%%%%%
Randpos = [];
for i = 1:(ceil(m/n))
Randpos = [Randpos,randperm(n)];
end
Tabu(:,1) = (Randpos(1,1:m))';
%%%第三步:m 只蚂蚁按概率函数选择下一座城市,完成各自的周游%%%%
for j = 2:n
for i = 1:m
visited = Tabu(i,1:(j-1)); %已访问的城市
J = zeros(1,(n-j+1)); %待访问的城市
P = J; %待访问城市的选择概率分布
Jc = 1;
for k = 1:n
if length(find(visited==k))==0
J(Jc) = k;
Jc = Jc+1;
end
end
%%%%%%%%%%%计算待选城市的概率分布%%%%%%%%%%%
for k = 1:length(J)
P(k) = (Tau(visited(end),J(k))^Alpha)...
*(Eta(visited(end),J(k))^Beta);
end
P = P/(sum(P));
%%%%%%%%%%%按概率原则选取下一个城市%%%%%%%%%
Pcum = cumsum(P);
Select = find(Pcum >= rand);
to_visit = J(Select(1));
Tabu(i,j) = to_visit;
end
end
if NC >= 2
Tabu(1,:) = R_best(NC-1,:);
end
%%%%%%%%%%%%%第四步:记录本次迭代最佳路线%%%%%%%%%%
L = zeros(m,1);
for i = 1:m
R = Tabu(i,:);
for j = 1:(n-1)
L(i) = L(i)+D(R(j),R(j+1));
end
L(i) = L(i)+D(R(1),R(n));
end
L_best(NC) = min(L);
pos = find(L==L_best(NC));
R_best(NC,:) = Tabu(pos(1),:);
%%%%%%%%%%%%%%%第五步:更新信息素%%%%%%%%%%%%%
Delta_Tau = zeros(n,n);
for i = 1:m
for j = 1:(n-1)
Delta_Tau(Tabu(i,j),Tabu(i,j+1)) = ...
Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
end
Delta_Tau(Tabu(i,n),Tabu(i,1)) = ...
Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
end
Tau = (1-Rho).*Tau+Delta_Tau;
%%%%%%%%%%%%%%%第六步:禁忌表清零%%%%%%%%%%%%%
Tabu = zeros(m,n);
%%%%%%%%%%%%%%%%%历代最优路线%%%%%%%%%%%%%%%
for i = 1:n-1
plot([ C(R_best(NC,i),1), C(R_best(NC,i+1),1)],...
[C(R_best(NC,i),2), C(R_best(NC,i+1),2)],'bo-');
hold on;
end
plot([C(R_best(NC,n),1), C(R_best(NC,1),1)],...
[C(R_best(NC,n),2), C(R_best(NC,1),2)],'ro-');
title(['优化最短距离:',num2str(L_best(NC))]);
hold off;
pause(0.005);
NC = NC+1;
end
%%%%%%%%%%%%%%%%%第七步:输出结果%%%%%%%%%%%%%%
Pos = find(L_best==min(L_best));
Shortest_Route = R_best(Pos(1),:); %最佳路线
Shortest_Length = L_best(Pos(1)); %最佳路线长度
figure(2),
plot(L_best)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
相关文章:

蚁群算法优化旅行问题
%%%%%%%%%%%%蚁群算法解决 TSP 问题%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%% clear all; %清除所有变量 close all; %清图 clc; %清屏 m 50; %蚂蚁个数 Alpha 1; %信息素重要程度参数 Beta 5; %启发式因子重要程度参数 Rho 0.1; %信息素蒸发系数 G 20…...

树数据结构
什么是树数据结构? 树数据结构是一种层次结构,用于以易于导航和搜索的方式表示和组织数据。它是由边连接的节点集合,节点之间具有层次关系。树的最顶端的节点称为根,它下面的节点称为子节点。每个节点可以有多个子节点,…...

Spring Boot整合Redis并提供多种实际场景的应用
Spring Boot整合Redis并提供多种实际场景的应用1. 整合Redis2. 场景应用2.1 缓存2.2 分布式锁2.3 计数器2.4 发布/订阅3. 总结Spring Boot是一个快速构建基于Spring框架的应用程序的工具,它提供了大量的自动化配置选项,可以轻松地集成各种不同的技术。Re…...
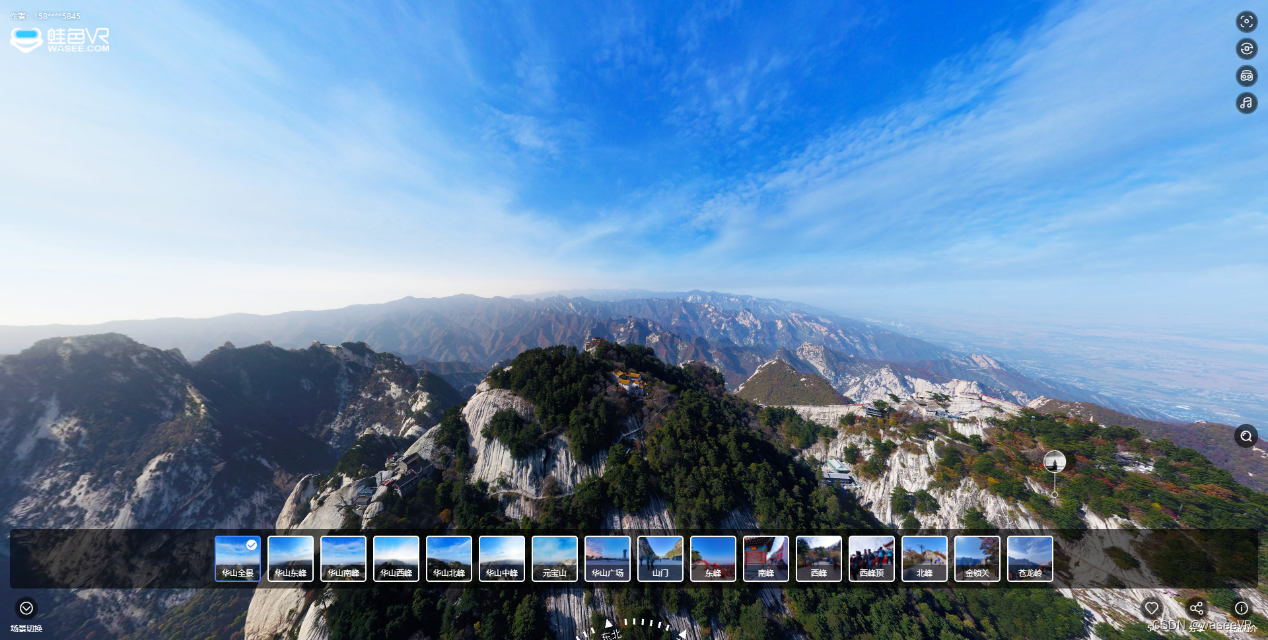
VR全景图片,助力VR全景制作,720全景效果图
VR全景图片是指通过全景相机或多相机组合拍摄全景画面,并进行拼接处理生成全景图像的过程。VR全景图片的应用范围广泛,包括旅游和景区、房地产、汽车、艺术和文化、电影和娱乐等领域。本文将详细介绍VR全景图片的类型、应用场景、市场前景和发展趋势。 一…...

Kali Linux20款重要软件
Kali Linux 是一个流行的网络安全测试平台,它包含了大量的工具和应用程序,以下是其中20款最常用的软件和工具: Metasploit:Metasploit 是一个广泛使用的漏洞评估工具,可以帮助安全专业人员测试系统中的漏洞。Aircrack…...

C语言测试五
windows是什么类型的系统(实时还是分时)?有什么区别? 分时操作系统。如果在单核的情况下,分时操作系统多个进程共用一个单核,该单核会将其执行时间分成相应的时间片,每个进程占用一定的时间片&a…...
【微服务~原始真解】Spring Cloud —— 访问数据库整合Druid数据源
🔎这里是【秒懂云原生】,关注我学习云原生不迷路 👍如果对你有帮助,给博主一个免费的点赞以示鼓励 欢迎各位🔎点赞👍评论收藏⭐️ 👀专栏介绍 【秒懂云原生】 目前主要更新微服务,…...

前端入门必刷题,经典算法—两数之和
优美的前⾔ 年轻的码农哟~ 你是不是⼀直在思考⾃我提升的问题~ 思来想去,决定从算法抓起(单押)~ 拿起⼜放下,经历过多少次放弃(单押 ✖ 2)~ 决定了!这次让我来帮你梳理(单押 ✖ 3&a…...

‘海外/国外‘地区微博签到shu据(正题在第二部分)
最近失眠,研究了项关于weibo爬虫的新功能,种种原因,大家可跳过第一部分的引用直接看第二部分。 内容来源:健康中国、生命时报、央视等 失眠标准一:3个“30分钟” ● 入睡困难,从躺下想睡到睡着间隔…...

Springboot——SB整合Mybatis的CURD(基于注解进行开发)
此处是根据需求实现基本操作 上面这里涉及到了条件分页查询,还有增加和批量删除员工信息,右边编辑就是先查询后更新操作,叫做查询回显,然后在原有基础上进行更新 环境准备 在下面的入门案例的整体环境下把数据库表换成empSpring…...

现在大专生转IT可行吗?
当然可行的。 大专也是人,为什么不可以选择喜欢的专业学习,现在大学生遍地都是,学历已经不是限制你发展的因素了。有的人就是不擅长理论学习,更喜欢技术。IT也只是一个普普通通的技术行业,跟其他技术行业一样…...

XC7A50T-1CSG324I、XC7A50T-2CSG324I Artix-7 FPGA可编程门阵列
Artix-7 FPGA能够在多个方面实现更高的性价比,这些方面包括逻辑、信号处理、嵌入式内存、LVDS I/O、内存接口,以及收发器。MicroBlaze CPU针对Xilinx FPGA进行了优化,是一种可高度配置的32位RISC处理器,可为微控制器、实时处理器和…...

linux安装图片处理软件ImageMagick
下载地址: wget https://download.imagemagick.org/archive/ImageMagick-7.1.1-4.tar.gz 或者 wget --no-check-certificate https://download.imagemagick.org/archive/ImageMagick-7.1.1-4.tar.gz 安装命令: tar -zxvf ImageMagick-7.1.1-4.tar.…...

【Java基础】JavaCore核心-反射技术
文章目录1.什么是反射技术2.反射-获取类对象方式3.反射-获取声明构造器4.反射-对象创建实战5.反射-方法和属性实战6.反射-属性值操作实战7.反射-invoke运行类方法1.什么是反射技术 Java的反射(reflection)机制是指在程序的运行状态中 可以构造任意一个类…...
)
AWGN后验估计下的均值与协方差关系(向量和标量形式)
文章目录AWGN信道向量模型后验均值与协方差的关系从实数域拓展到复数域小结AWGN信道向量模型 考虑一个随机向量x∼pX(x)\boldsymbol x \sim p_{\boldsymbol X}(\boldsymbol x)x∼pX(x),信道模型为 qxv,v∼N(0,Σ)\boldsymbol q \boldsymbol x \boldsymbol v, \…...

Linux常用命令之文件搜索命令
1、常用搜索-find 命令find英文原意find所在路径/bin/find执行权限所有用户功能描述文件搜索语法find [搜索范围] [搜索条件] (默认准确搜索)范例find /etc -name init?? 常用的搜索条件的选项包括: -name:按照文件名进行匹配查找,例&…...

ChatGPT给软件测试行业带来的可能
软件测试在软件开发过程中扮演着至关重要的角色,因为它可以确保软件的质量和可靠性。而随着人工智能技术的不断发展,ChatGPT作为一个强大的自然语言处理工具,可以在软件测试中发挥出许多重要的作用。本文将介绍ChatGPT在软件测试应用中带来的…...

Cadence Allegro 导出Properties on Nets Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Properties on Nets Report作用3,Properties on Nets Report示例4,Properties on Nets Report导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
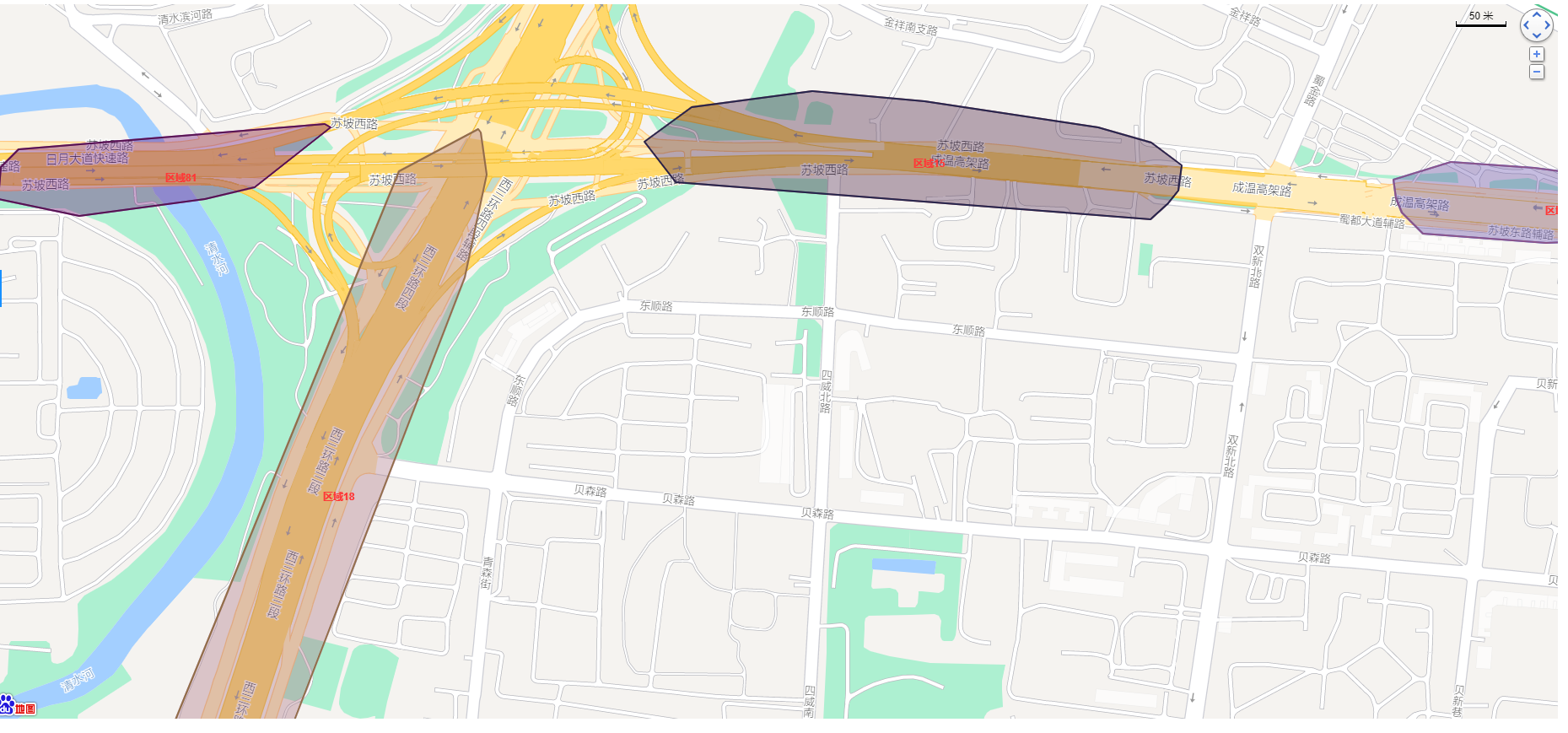
JAVA代码 实现定位数据动态聚集并绘制多边形区域
文章目录思路1、限制聚合距离2、绘制多边形区域3、多边形区域之间合并4、多边形定边点4、逻辑流程一些性能上的优化1、多边形设置圆心2、采用分支合并思路3、清理聚集较分散区域合理性处理1、解决多边形内凹角问题2、解决定边点插入位置问题3、多边形区域扩展成果展示最近有根据…...

基于储能进行调峰和频率调节研究【超线性增益的联合优化】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
