算法打卡:第十一章 图论part08
今日收获:拓扑排序,dijkstra算法
算法讲解部分均来源于代码随想录
1. 拓扑排序
基础知识:
(1)应用场景:给出有向图,将有向图转换为线性的排序就叫拓扑排序(如果图中有环则存在循环依赖,不能做线性排序,所以拓扑排序也可以用来判断有向图中是否有环)
(2)解法:卡恩算法(BFS广度优先搜索)
(3)步骤:
- 找到入度为0的点加入结果集
- 将该节点从图中移除
(4)图中有环:此时找不到入度为0的点,所以结果集的长度小于节点个数
题目链接:117. 软件构建 (kamacoder.com)
方法:
import java.util.*;public class Main{public static void main(String[] args){Scanner sc=new Scanner(System.in);int N=sc.nextInt();int M=sc.nextInt();// 记录节点的入度int[] inDegree=new int[N];// 记录依赖关系List<List<Integer>> edges=new ArrayList<>(N);for (int i=0;i<N;i++){edges.add(new ArrayList<>());}// 接收依赖关系for (int i=0;i<M;i++){int s=sc.nextInt();int t=sc.nextInt();edges.get(s).add(t); // 依赖于s的边inDegree[t]++;}// 队列存储入度为0的节点Queue<Integer> queue=new LinkedList<>();for (int i=0;i<N;i++){if (inDegree[i]==0){queue.offer(i);}}// 存储结果List<Integer> result=new ArrayList<>();while (!queue.isEmpty()){int cur=queue.poll();result.add(cur);// 将相连节点的入度减一for (int edge:edges.get(cur)){inDegree[edge]--;if (inDegree[edge]==0){queue.offer(edge);}}}// 判断是否存在环if (result.size()==N){for (int i=0;i<result.size()-1;i++){System.out.print(result.get(i)+" ");}System.out.print(result.get(N-1));}else {System.out.println(-1);}}
}2. dijkstra算法
基础知识:
(1)求最短路径问题:给出有向图,求起点到终点的最短路径。
(2)dijkstra算法:有向图中边的权值均为非负数;可以求起点到其他节点的最短路径算法
(3)dijkstra三部曲:minDist数组用来记录每一个节点距离源点的最小距离。
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
(4)如果需要打印边,和prim算法一样,在更新minDist数组时记录父节点
(5)和prim算法的区别:
- prim是求非访问节点到最小生成树的最小距离
- dijkstra是求非访问节点到源点的最小距离,源点是固定的
(6)要求非负权值是因为,此算法后续节点距离源节点的距离=前面节点到源节点的距离+本边的权值,后面的节点一定要比前面已加入路径中的节点成本大
题目链接:47. 参加科学大会(第六期模拟笔试) (kamacoder.com)
方法:
import java.util.*;public class Main{public static void main(String[] args){Scanner sc=new Scanner(System.in);int N=sc.nextInt();int M=sc.nextInt();boolean[] visited=new boolean[N+1]; // 记录是否访问int[][] grid=new int[N+1][N+1]; // 记录所有的边,初始化为不可达for(int i=0;i<N+1;i++){Arrays.fill(grid[i],Integer.MAX_VALUE);}for (int i=0;i<M;i++){int s=sc.nextInt();int e=sc.nextInt();int v=sc.nextInt();grid[s][e]=v;}int[] minDist=new int[N+1]; // 其他点到源点的最小距离for (int i=0;i<N+1;i++){minDist[i]=Integer.MAX_VALUE;}minDist[1]=0;// 求到原点的最小距离for (int i=1;i<N+1;i++){int cur=-1;int minD=Integer.MAX_VALUE;// 选择最小节点for (int j=1;j<N+1;j++){if (minDist[j]<minD&&!visited[j]){cur=j;minD=minDist[j];}}if (cur==-1){break;}// 标记访问visited[cur]=true;// 更新其他节点for (int j=1;j<N+1;j++){if (minDist[cur]+grid[cur][j]<minDist[j]&&!visited[j]&&grid[cur][j]!=Integer.MAX_VALUE){minDist[j]=minDist[cur]+grid[cur][j];}}}if (minDist[N]==Integer.MAX_VALUE){System.out.println(-1);}else {System.out.println(minDist[N]);}}
}相关文章:

算法打卡:第十一章 图论part08
今日收获:拓扑排序,dijkstra算法 算法讲解部分均来源于代码随想录 1. 拓扑排序 基础知识: (1)应用场景:给出有向图,将有向图转换为线性的排序就叫拓扑排序(如果图中有环则存在循…...

2024年Gartner主存储平台魔力象限报告 | 华为从领导者象限滑落到挑战者象限
魔力象限报告对比 本周Gartner发布了2024年主存储平台魔力象限报告,主存储用户正在采用平台原生服务功能来实现混合 IT 运营。I&O 领导者应利用这项研究来为任务关键型应用程序规划和执行现代且有弹性的存储基础设施平台。 本次报告中共有10家厂商入选…...

[Python学习日记-31] Python 中的函数(上)
[Python学习日记-31] Python 中的函数(上) 简介 语法定义 函数的参数 简介 引子: 你是某公司的一个高级程序员,现在老板让你写一个监控程序,需要24小时全年无休的监控公司网站服务器的系统状况,当 CPU、…...

工作笔记【四】
对于这种,样式一样,但是图片和字体颜色不一样,动态渲染。 代码: <template><view class"page"><view class"rows" v-for"item in data"><view class"v0"><v…...

ArcEngine C#二次开发图层处理:根据属性分割图层(Split)
需求:仅根据某一属性,分割图层,并以属性值命名图层名称保存。 众所周知,ArcGIS ArcToolbox中通过Split可以实现图形分割一个图层,以属性值命名图层,如下图所示。 本文仅仅依据属性值,将一个shp…...

【二叉平衡搜索树】Treap
前置 本篇是平衡树-treap的补充学习笔记。 Treap - 树堆 学习基础:适合一定基础的:比如,实现了经典二叉搜索树(常用的几个函数写过), 和二叉堆(数组的上浮下沉会写吗?)&a…...

Spring Boot 应用Kafka讲解和案例示范
Kafka 是一款高吞吐量、低延迟的分布式消息系统。本文将详细介绍如何在 Spring Boot 项目中使用 Kafka 进行消息接收与消费,并结合幂等和重试机制,确保消息消费的可靠性和系统的扩展性。我们将以电商交易系统为案例进行深入解析。 1. 系统架构概览 在电…...

以到手价为核心的品牌电商价格监测
在当今竞争激烈的电商时代,品牌的价格监测至关重要。传统的页面价监测已无法满足品牌对渠道管控的需求,而到手价监测则成为品牌控价的关键所在。 力维网络,作为深耕数据监测服务多年的专业机构,拥有自主开发的数据监测系统&#…...

Android中使用RecyclerView制作横向轮播列表及索引点
在Android开发中,RecyclerView是一个非常强大的组件,用于展示列表数据。它不仅支持垂直滚动,还能通过配置不同的LayoutManager实现横向滚动,非常适合用于制作轮播图或横向列表。本文将详细介绍如何使用RecyclerView在Android应用中…...

Llama 3.1 技术研究报告-2
3.3 基础设施、扩展性和效率 我们描述了⽀持Llama 3 405B⼤规模预训练的硬件和基础设施,并讨论了⼏项优化措施,这些措施提⾼了训练效率。 3.3.1 训练基础设施 Llama 1和2模型在Meta的AI研究超级集群(Lee和Sengupta,2022&#x…...

【深度学习】05-RNN循环神经网络-02- RNN循环神经网络的发展历史与演化趋势/LSTM/GRU/Transformer
RNN网络的发展历史与演化趋势 RNN(Recurrent Neural Network,循环神经网络)是一类用于处理序列数据的神经网络,特别擅长捕捉数据的时间或上下文依赖性。在其发展的过程中,不断出现各种改进和变体,以解决不…...

C++学习9.27
1、顺序表、栈、队列都更改成模板类 (1)顺序表 #include <iostream> #include <cstring>using namespace std;template <typename T1,typename T2,typename T3> class My_string { private:T1 *ptr; //指向字符数组的指针T2…...

【STM32开发环境搭建】-1-Keil(MDK) 5.27软件安装和注册教程
目录 1 安装前装备工作 2 安装KEIL(MDK-ARM) 5.27软件 3 注册KEIL(MDK-ARM) 5.27软件,获取License许可证 4 手动安装STM32F0,STM32F1,STM32F4,STM32F7,STM32H7的支持包 4.1 下载STM32的支持包 4.2 安装STM32的支…...

武汉正向科技格雷母线公司,无人天车系统,采用格雷母线定位技术
正向科技-格雷母线高精确定位技术-实操视频 高精度格雷母线内胆采用刚性内胆,基板采用精密度数控加工工艺,穿线卡采用高精度模具制作,不采用泡沫板填充,提高了地址检测精度和线性度。 最新一代的格雷母线定位技术特点是全数字化检…...
【保姆级教程】批量下载Pexels视频Python脚本(以HumanVid数据集为例)
目录 方案一:转换链接为download模式 方案二:获取源链接后下载 附录:HumanVid链接 方案一:转换链接为download模式 将下载链接的后缀加入 /download 然后用下面的脚本下载: import argparse import json import o…...
Python画笔案例-067 绘制配乐七角星
1、绘制橙子 通过 python 的turtle 库绘制 配乐七角星,如下图: 2、实现代码 绘制 配乐七角星 ,以下为实现代码: """配乐七角星.py本程序需要coloradd模块支持,安装方法:pip install coloradd""" import turtle from coloradd import color…...

Spark Job 对象 详解
在 Apache Spark 中,Job 对象是执行逻辑的核心组件之一,它代表了对一系列数据操作(如 transformations 和 actions)的提交。理解 Job 的本质和它在 Spark 中的运行机制,有助于深入理解 Spark 的任务调度、执行模型和容…...

C#中NModbus4中常用的方法
NModbus4 是一个用于 Modbus 协议通信的 C# 库,它支持串行 ASCII、RTU、TCP 和 UDP 协议。以下是 NModbus4 中常用的一些方法: 创建连接: ModbusSerialMaster.CreateRtu(SerialPort serialPort): 创建一个 RTU 串行连接。ModbusSerialMaster.…...
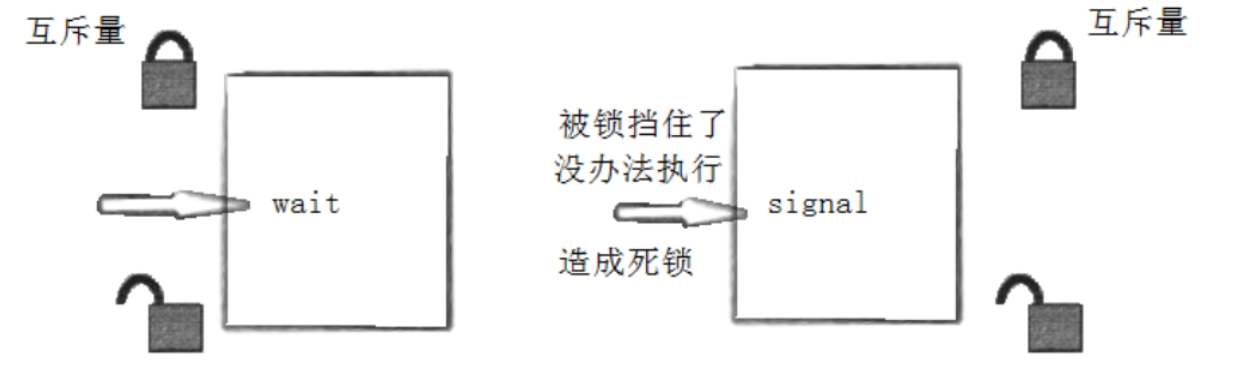
【Linux】线程同步与互斥
一、线程间互斥 1 .进程线程间的互斥相关概念 临界资源:多线程执行流共享的资源就叫做临界资源 临界区:每个线程内部,访问临界资源的代码,就叫做临界区 互斥:任何时刻,互斥保证有且只有一个执行流进入临界…...
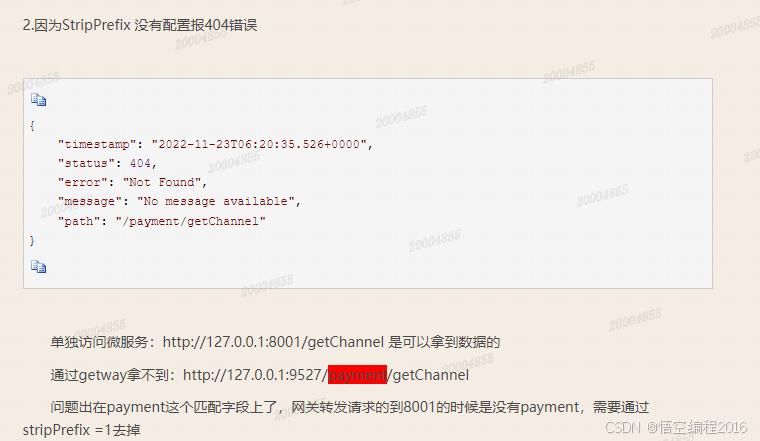
003、网关路由问题
1. nginx配置404跳转回默认路由 https://blog.csdn.net/masteryee/article/details/83689954 https://blog.csdn.net/IbcVue/article/details/133230460 https://www.jb51.net/server/317970ynk.htm https://blog.csdn.net/u014438244/article/details/120531287 https://blog…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...
