拉普拉斯矩阵
拉普拉斯算子
Δf=f(xi+1,yj)+f(xi−1,yj)+f(xi,yj+1)+f(xi,yj−1)−4f(xi,yj)=∑(k,l)∈N(i,j)(f(xk,yl)−f(xi,yj))\begin{aligned} \Delta f &= f\left(x_{i+1}, y_j\right) + f\left(x_{i-1},y_j\right) + f\left(x_i,y_{j+1}\right)+f\left(x_i,y_{j-1}\right) - 4f\left(x_i,y_j\right)\\ &=\sum\limits_{\left(k,l\right) \in N\left(i,j\right)}\left(f\left(x_k,y_l\right) - f\left(x_i,y_j\right)\right) \end{aligned} Δf=f(xi+1,yj)+f(xi−1,yj)+f(xi,yj+1)+f(xi,yj−1)−4f(xi,yj)=(k,l)∈N(i,j)∑(f(xk,yl)−f(xi,yj))
其中N(i,j)N\left(i,j\right)N(i,j)表示(i,j)\left(i,j\right)(i,j)相邻的节点,例如这里是四联通(上下左右)
拉普拉斯矩阵
前面的拉普拉斯算子是上下左右,而图的顶点的连接关系可以是任意的,下面将拉普拉斯算子推广到图。
如果将图的顶点处的值看作是函数值,则在顶点iii的拉普拉斯算子为
Δfi=∑j∈Ni(fi−fj)\Delta f_i = \sum_{j \in N_i}\left(f_i-f_j\right) Δfi=j∈Ni∑(fi−fj)
这里的拉普拉斯算子和上面的拉普拉斯算子查了个负号
(下面针对无向图)
由于图的边可以带有权重,设W\mathbf{W}W为邻接矩阵
Δfi=∑j∈Niwij(fi−fj)\Delta f_i = \sum_{j \in N_i}w_{ij}\left(f_i-f_j\right) Δfi=j∈Ni∑wij(fi−fj)
设VVV为顶点集合,n=∣V∣n = \left|V\right|n=∣V∣,D\mathbf{D}D为加权度矩阵,即dij={∑j=1nwij,i=j0,otherwised_{ij} = \begin{cases} \sum_{j=1}^{n}w_{ij},& i = j\\ 0,&otherwise\\ \end{cases}dij={∑j=1nwij,0,i=jotherwise
如果j∉Nij\notin N_ij∈/Ni则wij=0w_{ij} = 0wij=0,于是
Δfi=∑j∈Vwij(fi−fj)=∑j∈Vwijfi−∑j∈Vwijfj=diifi−wif\Delta f_i = \sum_{j \in V}w_{ij}\left(f_i-f_j\right) = \sum_{j \in V}w_{ij}f_i - \sum_{j \in V}w_{ij}f_j = d_{ii} f_i - \mathbf{w}_i\mathbf{f} Δfi=j∈V∑wij(fi−fj)=j∈V∑wijfi−j∈V∑wijfj=diifi−wif
其中wI\mathbf{w}_IwI表示W\mathbf{W}W的第iii行,f=(f1f2⋮fn)\mathbf{f} = \begin{pmatrix} f_1\\ f_2\\ \vdots\\ f_n\\ \end{pmatrix}f=f1f2⋮fn
对于所有的点,有
Δf=(Δf1⋮Δfn)=(d1f1−w1f⋮dnfn−wnf)=Df−Wf=(D−W)f\Delta f = \begin{pmatrix} \Delta f_1\\ \vdots \\ \Delta f_n \end{pmatrix} = \begin{pmatrix} d_1 f_1 - \mathbf{w}_1 \mathbf{f}\\ \vdots \\ d_n f_n - \mathbf{w}_n \mathbf{f}\\ \end{pmatrix}=\mathbf{D}\mathbf{f} - \mathbf{W}\mathbf{f} = \left(\mathbf{D} - \mathbf{W} \right) \mathbf{f} Δf=Δf1⋮Δfn=d1f1−w1f⋮dnfn−wnf=Df−Wf=(D−W)f
定义拉普拉斯矩阵为
L=D−W\mathbf{L} = \mathbf{D} - \mathbf{W} L=D−W
性质
性质1
∀f∈Rn\forall \mathbf{f}\in\mathbb{R}^n∀f∈Rn,有
fTLf=12∑i=1n∑j=1nwij(fi−fj)2\mathbf{f}^T\mathbf{L}\mathbf{f}=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij}\left(f_i-f_j\right)^2 fTLf=21i=1∑nj=1∑nwij(fi−fj)2
证明:
fTLf=fTDf−fTWf=∑i=1ndiifi2−∑i=1n∑j=1nfifjwij=12(2∑i=1ndiifi2−2∑i=1n∑j=1nfifjwij)=12(∑i=1ndiifi2−2∑i=1n∑j=1nfifjwij+∑j=1ndjjfj2)=12(∑i=1n∑j=1nwijfi2−2∑i=1n∑j=1nfifjwij+∑j=1n∑i=1nwjifj2)=12(∑i=1n∑j=1nwijfi2−2∑i=1n∑j=1nfifjwij+∑i=1n∑j=1nwjifj2)=12(∑i=1n∑j=1nwijfi2−2∑i=1n∑j=1nfifjwij+∑i=1n∑j=1nwijfj2)=12∑i=1n∑j=1nwij(fi−fj)2\begin{aligned} \mathbf{f}^T\mathbf{L}\mathbf{f} &= \mathbf{f}^T\mathbf{D}\mathbf{f} - \mathbf{f}^T\mathbf{W} \mathbf{f}\\ &=\sum_{i=1}^{n}d_{ii} f_i^2 - \sum_{i=1}^{n}\sum_{j=1}^{n}f_i f_j w_{ij}\\ &=\frac{1}{2}\left(2\sum_{i=1}^{n}d_{ii} f_i^2 - 2\sum_{i=1}^{n}\sum_{j=1}^{n}f_i f_j w_{ij}\right)\\ &=\frac{1}{2}\left(\sum_{i=1}^{n}d_{ii} f_i^2 - 2\sum_{i=1}^{n}\sum_{j=1}^{n}f_i f_j w_{ij} + \sum_{j=1}^{n}d_{jj} f_j^2\right)\\ &=\frac{1}{2}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij} f_i^2 - 2\sum_{i=1}^{n}\sum_{j=1}^{n}f_i f_j w_{ij} + \sum_{j=1}^{n}\sum_{i=1}^{n}w_{ji} f_j^2\right)\\ &=\frac{1}{2}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij} f_i^2 - 2\sum_{i=1}^{n}\sum_{j=1}^{n}f_i f_j w_{ij} + \sum_{i=1}^{n}\sum_{j=1}^{n}w_{ji} f_j^2\right)\\ &=\frac{1}{2}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij} f_i^2 - 2\sum_{i=1}^{n}\sum_{j=1}^{n}f_i f_j w_{ij} + \sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij} f_j^2\right)\\ &=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij}\left(f_i-f_j\right)^2 \end{aligned} fTLf=fTDf−fTWf=i=1∑ndiifi2−i=1∑nj=1∑nfifjwij=21(2i=1∑ndiifi2−2i=1∑nj=1∑nfifjwij)=21(i=1∑ndiifi2−2i=1∑nj=1∑nfifjwij+j=1∑ndjjfj2)=21(i=1∑nj=1∑nwijfi2−2i=1∑nj=1∑nfifjwij+j=1∑ni=1∑nwjifj2)=21(i=1∑nj=1∑nwijfi2−2i=1∑nj=1∑nfifjwij+i=1∑nj=1∑nwjifj2)=21(i=1∑nj=1∑nwijfi2−2i=1∑nj=1∑nfifjwij+i=1∑nj=1∑nwijfj2)=21i=1∑nj=1∑nwij(fi−fj)2
性质2
L⪰0\mathbf{L}\succeq 0 L⪰0
由性质1,显然
性质3
最小特征值为0,对应的特征向量为e\mathbf{e}e,即全1的向量
证明:
每一行加起来
∑j=1nlij=∑j=1n(dij−wij)=dii−∑j=1nwij=0\sum_{j=1}^{n} l_{ij} = \sum_{j=1}^{n}\left(d_{ij} - w_{ij}\right) = d_{ii}-\sum_{j=1}^{n}w_{ij} = 0∑j=1nlij=∑j=1n(dij−wij)=dii−∑j=1nwij=0
于是Le=0e\mathbf{L}\mathbf{e} = 0\mathbf{e}Le=0e
性质4
设G\mathbf{G}G是一个非负权重的无向图,则其拉普拉斯矩阵L\mathbf{L}L的特征值0的重数kkk等于图的连通分量的个数
证明:
当k=1k=1k=1时,即连通图
fTLf=12∑i=1n∑j=1nwij(fi−fj)2=12∑(i,j)wij(fi−fj)2=0\mathbf{f}^T\mathbf{L}\mathbf{f}=\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij}\left(f_i-f_j\right)^2=\frac{1}{2}\sum_{\left(i,j\right)}w_{ij}\left(f_i-f_j\right)^2=0 fTLf=21i=1∑nj=1∑nwij(fi−fj)2=21(i,j)∑wij(fi−fj)2=0
对于wij>0w_{ij}>0wij>0,有fi=fjf_i = f_jfi=fj
由于是连通图,最后f1=f2=⋯=fnf_1 = f_2 = \cdots = f_nf1=f2=⋯=fn(有点像并查集)
也就是说当且仅当f=te(t≠0)\mathbf{f} = t\mathbf{e}\left(t\neq 0\right)f=te(t=0)时,fTLf=0\mathbf{f}^T\mathbf{L}\mathbf{f} = 0fTLf=0
因为特征值000对应的特征向量只有tet\mathbf{e}te,所以重数为1
假设k−1k-1k−1的时候成立
kkk时
不妨假设顶点按照其所属的联通分量排序
则对应的拉普拉斯矩阵是一个分块矩阵,
L=(L1L2⋱Lk)\mathbf{L} = \begin{pmatrix} \mathbf{L}_1&&& \\ &\mathbf{L}_2&&\\ &&\ddots&\\ &&&\mathbf{L}_k \end{pmatrix} L=L1L2⋱Lk
令f=(0⋮01⋮10⋮0)\mathbf{f} = \begin{pmatrix} 0\\ \vdots\\ 0\\ 1\\ \vdots\\ 1\\ 0\\ \vdots\\ 0\\ \end{pmatrix}f=0⋮01⋮10⋮0,每一个分块矩阵对应的分量为1,剩下的为0
有fTLf=0\mathbf{f}^T\mathbf{L}\mathbf{f} = 0fTLf=0
这样的f\mathbf{f}f有kkk个
归一化拉普拉斯矩阵
对称归一化
盲猜针对无向图,并且没有孤立点和自环,这样才能保证dii≠0,wii=0,wij=wjid_{ii} \neq 0,w_{ii} = 0,w_{ij} = w_{ji}dii=0,wii=0,wij=wji
定义为
Lsym=D−12LD−12=I−D−12WD−12\mathbf{L}_{sym} = \mathbf{D}^{-\frac{1}{2}}\mathbf{L}\mathbf{D}^{-\frac{1}{2}} = \mathbf{I}-\mathbf{D}^{-\frac{1}{2}}\mathbf{W}\mathbf{D}^{-\frac{1}{2}} Lsym=D−21LD−21=I−D−21WD−21
显然这是一个对称,[lsym]ij={1i=j−wijdiidjj,wij≠00,otherwise\left[l_{sym}\right]_{ij} = \begin{cases} 1&i = j\\ -\frac{w_{ij}}{\sqrt{d_{ii}d_{jj}}},&w_{ij}\neq 0\\ 0,&otherwise\\ \end{cases}[lsym]ij=⎩⎨⎧1−diidjjwij,0,i=jwij=0otherwise
相关文章:

拉普拉斯矩阵
拉普拉斯算子 Δff(xi1,yj)f(xi−1,yj)f(xi,yj1)f(xi,yj−1)−4f(xi,yj)∑(k,l)∈N(i,j)(f(xk,yl)−f(xi,yj))\begin{aligned} \Delta f & f\left(x_{i1}, y_j\right) f\left(x_{i-1},y_j\right) f\left(x_i,y_{j1}\right)f\left(x_i,y_{j-1}\right) - 4f\left(x_i,y_j\r…...
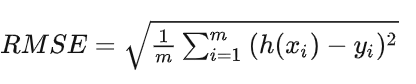
Top-1错误率、Top-5错误率等常见的模型算法评估指标解析
Top-1 错误率:指预测输出的概率最高的类别与人工标注的类别相符的准确率,就是你预测的label取最后概率向量里面最大的那一个作为预测结果,如过你的预测结果中概率最大的那个分类正确,则预测正确,否则预测错误。比如预测…...

Urho3D 容器类型
Urho3D实现了自己的字符串类型和模板容器,而不是使用STL。其基本原理如下: 在某些情况下提高了性能,例如使用PODVector类时。保证字符串和容器的二进制大小,以允许例如嵌入Variant对象内。减少了编译时间。直接命名和实现&#x…...
: 循环结构程序设计)
C语言学习笔记(四): 循环结构程序设计
while语句 定义 While语句是C语言中的循环语句,它按条件循环执行语句,直到条件不满足为止 语法格式如下: while(condition) {//循环体内容; }使用实例 求123…100 include <stdio.h> int main(){int i 1, sum 0;while (i<100){sum i …...

02 OpenCV图像通道处理
1 通道提取与合并 在数字图像处理中,图像通道是指一个图像中的颜色信息被分离为不同的颜色分量。常见的图像通道包括RGB通道、灰度通道、HSV通道等。 RGB通道是指将图像分离为红色、绿色和蓝色三个颜色通道,每个通道表示相应颜色的亮度。这种方式是最常…...
微信小程序图书馆座位预约管理系统
开发工具:IDEA、微信小程序服务器:Tomcat9.0, jdk1.8项目构建:maven数据库:mysql5.7前端技术:vue、uniapp服务端技术:springbootmybatis本系统分微信小程序和管理后台两部分,项目采用…...

有限元分析学习一
系列文章目录 有限元分析学习一 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录系列文章目录前言一、有限元方法的简单介绍1.1 有限元的基础概念1.2 有限元软件发展历史1.3 有限元软件二、弹性力学的简单介绍2.1.…...

android avb2.0 总结
1、android vbmeta结构深入解析 2、android libavb深入解读 看完结构与代码,进一步了解了avb 比如vbmeta的结构、5种描述符、hash公钥签名存储位置 多层vbmeta结构、无vbmeta分区的验证逻辑、hash计算对比、公钥验证、签名验签、5种描述符体的处理 但是还有一些问题没有解决 如…...

聊天机器人-意图识别类,开源库推荐
随着人工智能和自然语言处理技术的不断发展,聊天机器人在商业、教育、医疗等领域的应用越来越广泛。因此,开源聊天机器人代码库也逐渐成为了热门话题。 开源聊天机器人代码库可以帮助开发者快速构建功能强大的聊天机器人,而不必从头开始编写…...

Java 标识符以及修饰符
Java 标识符Java 所有的组成部分都需要名字。类名、变量名以及方法名都被称为标识符。关于 Java 标识符,有以下几点需要注意:所有的标识符都应该以字母(A-Z 或者 a-z),美元符($)、或者下划线(_&…...
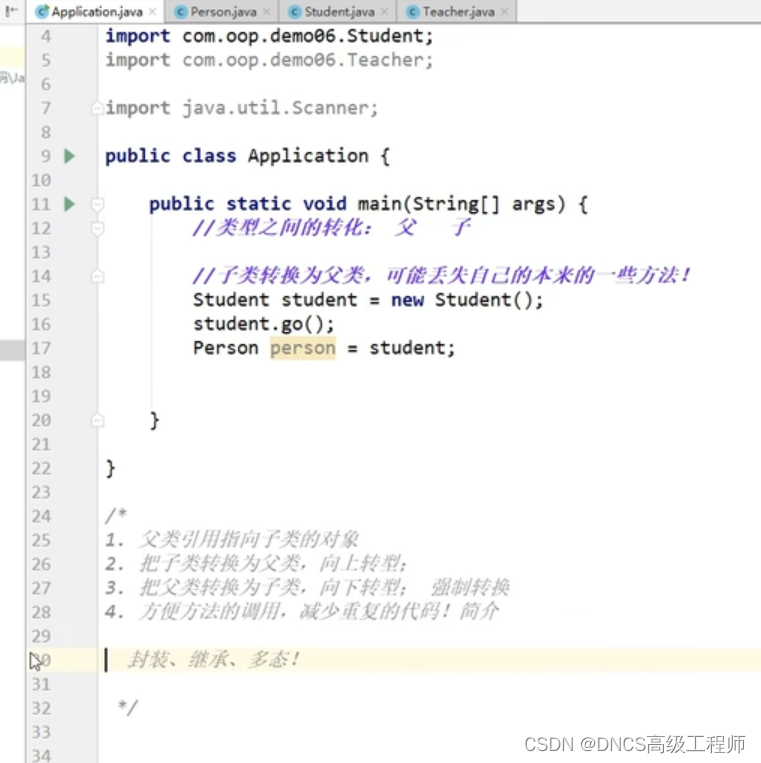
封装、继承、Super、重写、多态instanceof类型转换的使用以及个人见解
这里写目录标题封装继承supersuper和this的区别重写多态instanceof类型转换封装 之前我们调用共有的属性,是直接可以调用的 但是属性私有后,无法在直接.调用 只能通过getset调用 继承 super 可以直接调用父类中属性和方法,私有的无法做 其…...

day13_面向对象的三大特征之一(封装)
封装概述 为什么需要封装? 现实生活中,每一个个体与个体之间是有边界的,每一个团体与团体之间是有边界的,而同一个个体、团体内部的信息是互通的,只是对外有所隐瞒。例如:我们使用的电脑,内部…...
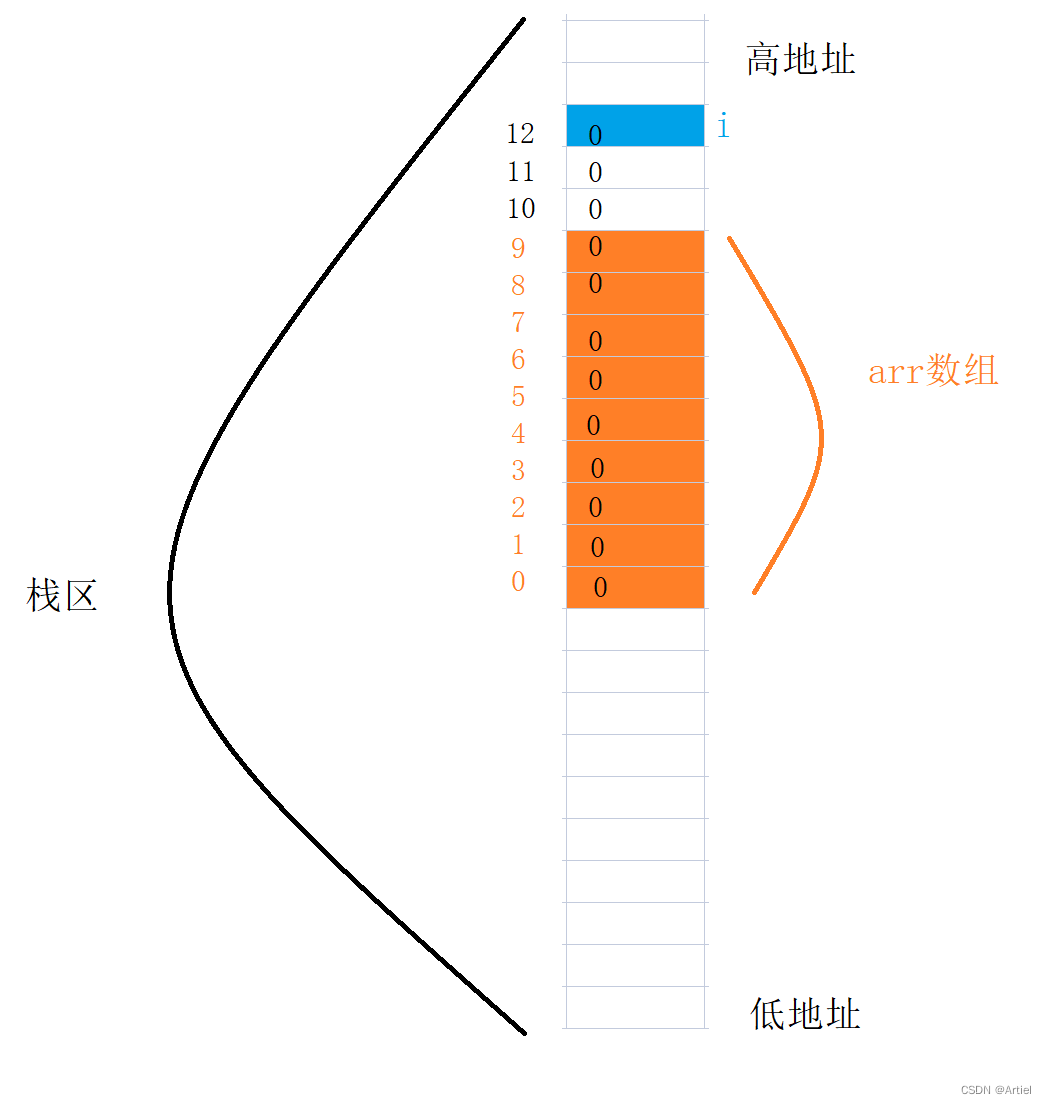
越界访问数组
越界访问是指访问(操作修改)了不属于自己的空间 我们以如下代码为例:此代码在vs中进行 #include <stdio.h> int main() {int i 0;int arr[] {1,2,3,4,5,6,7,8,9,10};for(i0; i<12; i){arr[i] 0;printf("hello\n");}r…...
软件设计(十)--计算机系统知识
软件设计(九)https://blog.csdn.net/ke1ying/article/details/128990035 一、效验码 奇偶效验:是一种最简单的效验方法。基本思想是:通过在编码中增加一个效验位来使编码中1的个数为奇数(奇效验)或者为偶…...
【不知道是啥】浅保存哈
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注…...

2021 WAIC 世界人工智能大会参会总结
前言 2021 年世界人工智能大会(WAIC)于2021年7月7日至10日在上海世博展览馆举办,本届大会继续秉持「智联世界」的理念,以「众智成城」为主题,促进全球人工智能创新思想、技术、应用、人才和资本的集聚和交流ÿ…...
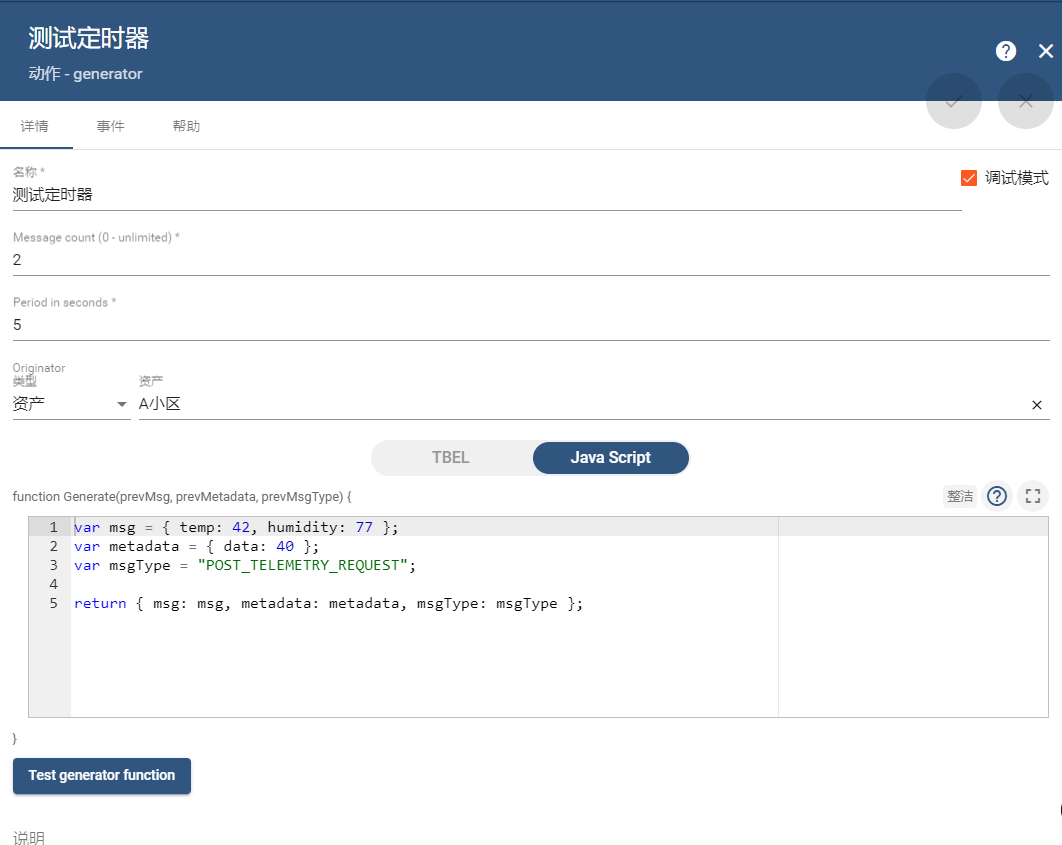
ThingsBoard-实现定时任务调度器批量RPC
1、概述 ThingsBoard-CE版是不支持调度器的,只有PE版才支持,但是系统中很多时候需要使用调度器来实现功能,例如:定时给设备下发rpc查询数据,我们如何来实现呢?下面我将教你使用巧妙的方法来实现。 2、使用什么实现 我们可以使用规则链提供的一个节点来实现,这个节点可…...

MySQL数据库调优————数据库调优维度及测试数据准备
MySQL性能优化金字塔法则 不合理的需求,会造成很多问题。(比如未分页,数据需要多表联查等)做架构设计的时候,应充分考虑业务的实际情况,考虑好数据库的各种选择(比如是否要读写分离,…...

电子货架标签多种固定方式
2.1寸和2.9寸电子价格标签多种固定方式: 1、桌面支架,放置在桌面或是货架上,用于桌面产品的价格或是信息显示 2、粘贴架,方便用于墙面桌面等应用 3、半透明支架,用于货架上的商品吊挂显示价格信息 4、轨道架ÿ…...
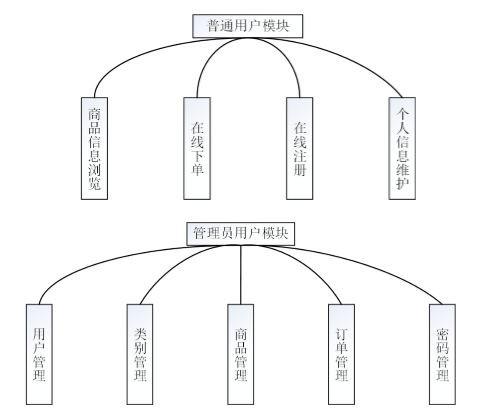
基于JavaEE的智能化跨境电子商务平台的设计
技术:Java、JSP、框架等摘要:伴随着近年来互联网的迅猛发展,网上零售逐渐成为了一种影响广泛、方便快捷的购物渠道。我国网上零售业发展的步伐很快。在如今经济全球化的影响下,消费者的网购行为趋于开放化、多元化,对于…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
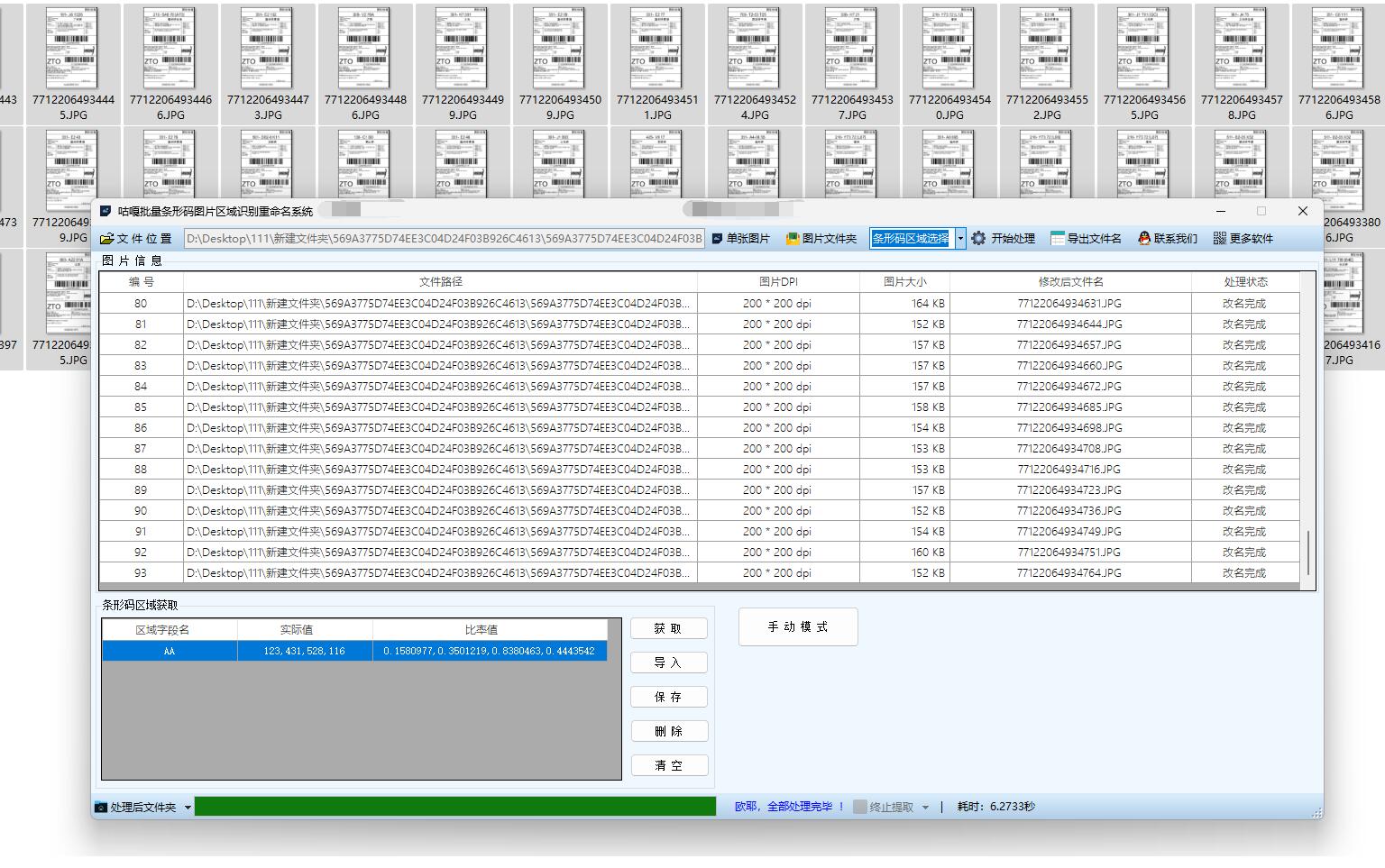
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...
