a = Sw,其中a和w是向量,S是矩阵,求w等于什么?w可以写成关于a和S的什么样子的公式
给定公式:
a = S w a = S w a=Sw
其中:
- a a a 是已知向量,
- S S S 是已知矩阵,
- w w w 是未知向量。
我们的目标是求解 w w w,即将 w w w 表示为 a a a 和 S S S 的函数。
情况 1:矩阵 S S S 可逆
如果矩阵 S S S 是可逆矩阵,即 S S S 是方阵(行数等于列数)且行列式不为零,那么 S S S 存在逆矩阵 S − 1 S^{-1} S−1。在这种情况下,可以直接求解:
w = S − 1 a \boxed{w = S^{-1} a} w=S−1a
步骤:
-
计算 S S S 的逆矩阵 S − 1 S^{-1} S−1:
- 仅当 S S S 为方阵且满秩(行列式不为零)时,逆矩阵 S − 1 S^{-1} S−1 存在。
-
计算 w w w:
w = S − 1 a w = S^{-1} a w=S−1a
示例:
设:
S = ( 2 1 0 1 ) , a = ( 5 1 ) S = \begin{pmatrix} 2 & 1 \\ 0 & 1 \end{pmatrix}, \quad a = \begin{pmatrix} 5 \\ 1 \end{pmatrix} S=(2011),a=(51)
计算 S − 1 S^{-1} S−1:
S − 1 = ( 1 2 − 1 2 0 1 ) S^{-1} = \begin{pmatrix} \frac{1}{2} & -\frac{1}{2} \\ 0 & 1 \end{pmatrix} S−1=(210−211)
求解 w w w:
w = S − 1 a = ( 1 2 − 1 2 0 1 ) ( 5 1 ) = ( 1 2 × 5 − 1 2 × 1 1 × 1 ) = ( 2 1 ) w = S^{-1} a = \begin{pmatrix} \frac{1}{2} & -\frac{1}{2} \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 5 \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{1}{2} \times 5 - \frac{1}{2} \times 1 \\ 1 \times 1 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} w=S−1a=(210−211)(51)=(21×5−21×11×1)=(21)
情况 2:矩阵 S S S 不可逆或非方阵
如果矩阵 S S S 不可逆(行列式为零)或是一个非方矩阵(行数不等于列数),则不能直接计算逆矩阵。在这种情况下,可以使用广义逆矩阵(Moore-Penrose 伪逆)来求解。
求解步骤:
-
计算 S S S 的伪逆矩阵 S + S^{+} S+:
- S + S^{+} S+ 满足 S + = ( S T S ) − 1 S T S^{+} = (S^T S)^{-1} S^T S+=(STS)−1ST,当 S T S S^T S STS 可逆时。
- 对于更一般的情况,可以使用奇异值分解(SVD)来计算 S + S^{+} S+。
-
计算 w w w:
w = S + a \boxed{w = S^{+} a} w=S+a
注意:
- 当方程组有唯一解时, w = S + a w = S^{+} a w=S+a 给出唯一解。
- 当方程组有无穷多解时, w = S + a w = S^{+} a w=S+a 给出最小范数解。
- 当方程组无解(即 a a a 不在 S S S 的列空间内)时, w = S + a w = S^{+} a w=S+a 给出使 ∥ S w − a ∥ 2 \| S w - a \|_2 ∥Sw−a∥2 最小的解。
示例:
设:
S = ( 1 2 3 4 5 6 ) , a = ( 7 8 9 ) S = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix}, \quad a = \begin{pmatrix} 7 \\ 8 \\ 9 \end{pmatrix} S= 135246 ,a= 789
S S S 是一个 3 × 2 3 \times 2 3×2 的矩阵,无法直接求逆。
计算 S S S 的伪逆 S + S^{+} S+:
-
计算 S T S S^T S STS:
S T S = ( 1 3 5 2 4 6 ) ( 1 2 3 4 5 6 ) = ( 35 44 44 56 ) S^T S = \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} = \begin{pmatrix} 35 & 44 \\ 44 & 56 \end{pmatrix} STS=(123456) 135246 =(35444456) -
计算 ( S T S ) − 1 (S^T S)^{-1} (STS)−1:
( S T S ) − 1 = 1 35 × 56 − 4 4 2 ( 56 − 44 − 44 35 ) ≈ ( 1.4 − 1.1 − 1.1 0.875 ) (S^T S)^{-1} = \frac{1}{35 \times 56 - 44^2} \begin{pmatrix} 56 & -44 \\ -44 & 35 \end{pmatrix} \approx \begin{pmatrix} 1.4 & -1.1 \\ -1.1 & 0.875 \end{pmatrix} (STS)−1=35×56−4421(56−44−4435)≈(1.4−1.1−1.10.875) -
计算 S + = ( S T S ) − 1 S T S^{+} = (S^T S)^{-1} S^T S+=(STS)−1ST:
S + = ( 1.4 − 1.1 − 1.1 0.875 ) ( 1 3 5 2 4 6 ) = ( − 0.2 0 0.2 0.15 0 − 0.15 ) S^{+} = \begin{pmatrix} 1.4 & -1.1 \\ -1.1 & 0.875 \end{pmatrix} \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix} = \begin{pmatrix} -0.2 & 0 & 0.2 \\ 0.15 & 0 & -0.15 \end{pmatrix} S+=(1.4−1.1−1.10.875)(123456)=(−0.20.15000.2−0.15) -
计算 w = S + a w = S^{+} a w=S+a:
w = ( − 0.2 0 0.2 0.15 0 − 0.15 ) ( 7 8 9 ) = ( ( − 0.2 ) × 7 + 0 × 8 + 0.2 × 9 0.15 × 7 + 0 × 8 + ( − 0.15 ) × 9 ) = ( 0.4 0 ) w = \begin{pmatrix} -0.2 & 0 & 0.2 \\ 0.15 & 0 & -0.15 \end{pmatrix} \begin{pmatrix} 7 \\ 8 \\ 9 \end{pmatrix} = \begin{pmatrix} (-0.2) \times 7 + 0 \times 8 + 0.2 \times 9 \\ 0.15 \times 7 + 0 \times 8 + (-0.15) \times 9 \end{pmatrix} = \begin{pmatrix} 0.4 \\ 0 \end{pmatrix} w=(−0.20.15000.2−0.15) 789 =((−0.2)×7+0×8+0.2×90.15×7+0×8+(−0.15)×9)=(0.40)
总结
- 当 S S S 可逆时, w = S − 1 a w = S^{-1} a w=S−1a。
- 当 S S S 不可逆或非方阵时, w = S + a w = S^{+} a w=S+a,其中 S + S^{+} S+ 是 S S S 的伪逆矩阵。
注意事项
- 求逆矩阵的条件:只有当矩阵 S S S 满足可逆条件(方阵且满秩)时,才可以直接求逆。
- 计算伪逆的方法:对于任意矩阵 S S S,都可以使用奇异值分解(SVD)来计算其伪逆 S + S^{+} S+。
- 数值计算:在实际计算中,建议使用数学软件(如 MATLAB、NumPy 等)来计算逆矩阵或伪逆矩阵,以避免手算过程中的误差。
相关文章:

a = Sw,其中a和w是向量,S是矩阵,求w等于什么?w可以写成关于a和S的什么样子的公式
给定公式: a S w a S w aSw 其中: a a a 是已知向量, S S S 是已知矩阵, w w w 是未知向量。 我们的目标是求解 w w w,即将 w w w 表示为 a a a 和 S S S 的函数。 情况 1:矩阵 S S S 可逆 如果矩…...

多线程事务管理:Spring Boot 实现全局事务回滚
多线程事务管理:Spring Boot 实现全局事务回滚 在日常开发中,我们常常会遇到需要在多线程环境下进行数据库操作的场景。这类操作的挑战在于如何保证多个线程中的数据库操作要么一起成功,要么一起失败,即 事务的原子性。尤其是在多个线程并发执行的情况下,确保事务的一致性…...
Vue3 中集成海康 H5 监控视频播放功能
🌈个人主页:前端青山 🔥系列专栏:Vue篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来Vuet篇专栏内容:Vue-集成海康 H5 监控视频播放功能 目录 一、引言 二、环境搭建 三、代码解析 子组件部分 1.…...

Linux: eBPF: libbpf-bootstrap-master 编译
文章目录 简介编译运行展示输出展示:简介 这个是使用libbpf的一个例子; 编译 如果是一个可以联网的机器,这个libbpf-bootstrap的编译就方便了,完全是自动化的下载依赖文件;如果没有,就只能自己准备这些个软件。 需要:libbpf-static; [root@RH8-LCP c]# makeLIB …...
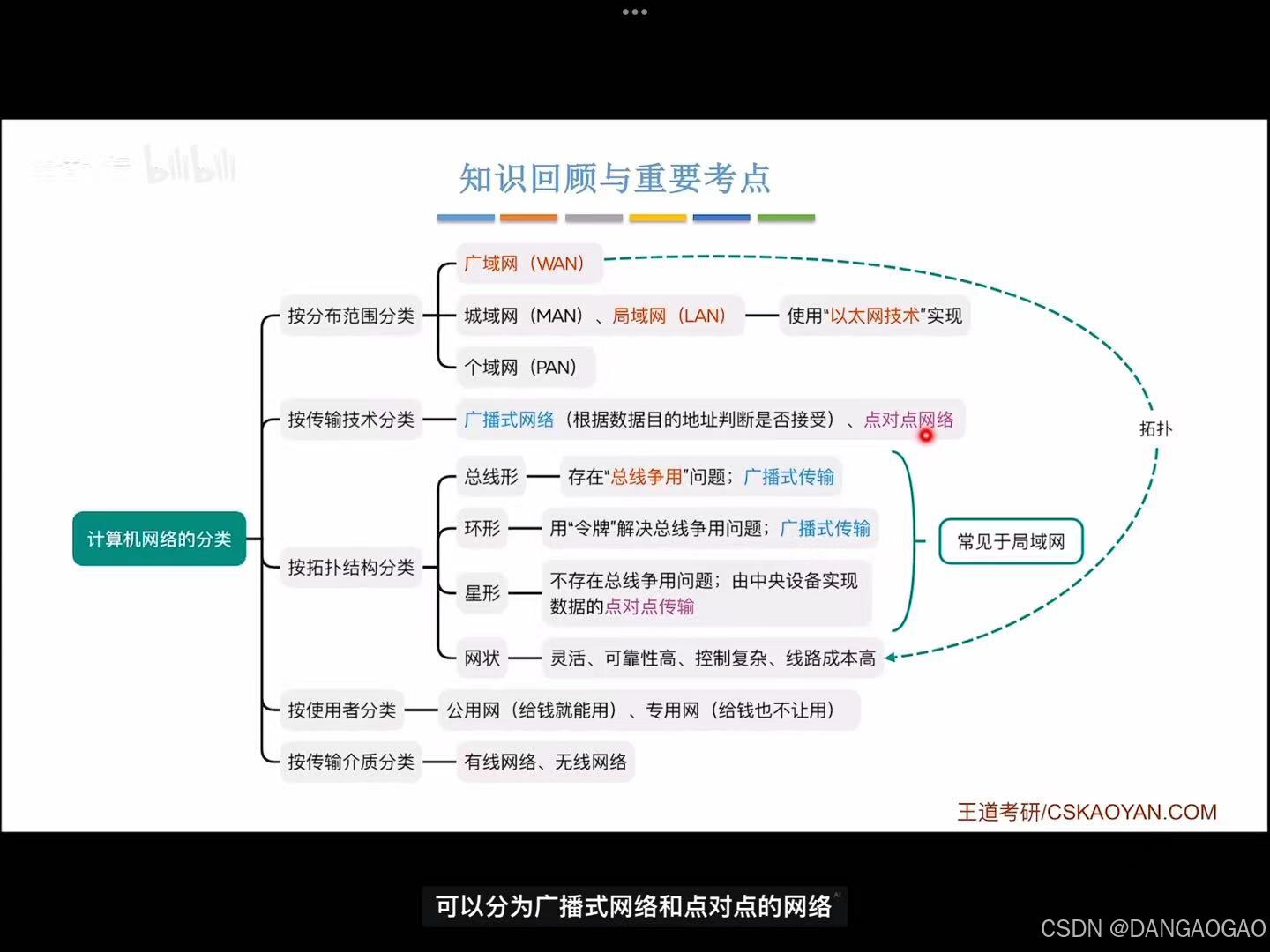
1.1.4 计算机网络的分类
按分布范围分类: 广域网(wan) 城域网(man) 局域网(lan) 个域网(pan) 注意:如今局域网几乎采用“以太网技术实现”,因此“以太网”几乎成了“局域…...

周家庄智慧旅游小程序
项目概述 周家庄智慧旅游小程序将通过数字化手段提升游客的旅游体验,依托周家庄的自然与文化资源,打造智慧旅游新模式。该小程序将结合虚拟现实(VR)、增强现实(AR)和人工智能等技术,提供丰富的…...

【在Linux世界中追寻伟大的One Piece】命名管道
目录 1 -> 命名管道 1.1 -> 创建一个命名管道 1.2 -> 匿名管道与命名管道的区别 1.3 -> 命名管道的打开规则 1.4 -> 例子 1 -> 命名管道 管道应用的一个限制就是只能在具有共同祖先(具有亲缘关系)的进程间通信。如果我们想在不相关的进程之间交换数据&…...
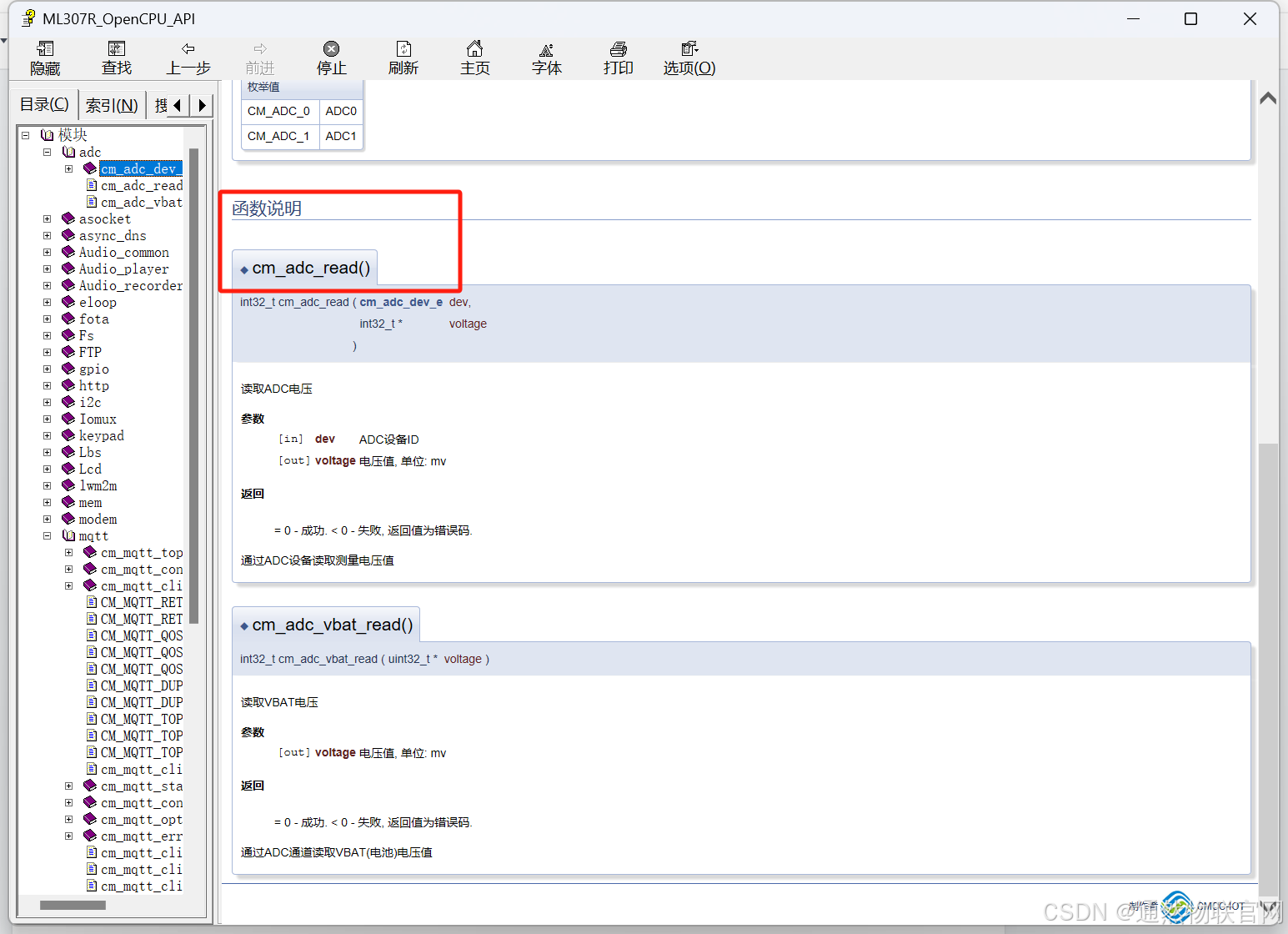
如意控物联网项目-ML307R模组软件及硬件调试环境搭建
软件及硬件调试环境搭建 1、 软件环境搭建及编译 a) 打开官方SDK,内涵APP-DEMO,通过vscode打开程序, 软件程序编写及编译参考下边说明文档链接 OneMO线上服务平台 编译需预安装python3.7以上版本,安装完python后,打开…...

大模型分布式训练并行技术(九)-总结
近年来,随着Transformer、MOE架构的提出,使得深度学习模型轻松突破上万亿规模参数,传统的单机单卡模式已经无法满足超大模型进行训练的要求。因此,我们需要基于单机多卡、甚至是多机多卡进行分布式大模型的训练。 而利用AI集群&a…...

uniapp view设置当前view之外的点击事件
推荐学习文档 golang应用级os框架,欢迎stargolang应用级os框架使用案例,欢迎star案例:基于golang开发的一款超有个性的旅游计划app经历golang实战大纲golang优秀开发常用开源库汇总想学习更多golang知识,这里有免费的golang学习笔…...

【Mybatis篇】动态SQL的详细带练
🧸安清h:个人主页 🎥个人专栏:【计算机网络】 🚦作者简介:一个有趣爱睡觉的intp,期待和更多人分享自己所学知识的真诚大学生。 文章目录 🎯一.动态SQL简单介绍 🚦动态S…...

【MyBatis-Plus】 学习记录 常用功能及代码生成器使用
文章目录 1. 环境准备2. 创建基础实体类3. 编写 Mapper 接口4. Service 层5. 控制器层6. 分页功能7. 条件构造器8. 配置乐观锁9. 常见问题10. 代码生成器1. 创建数据库表2. 引入依赖3. 配置数据库连接4. 编写代码生成器5. 运行代码生成器6. 查看生成的代码 MyBatis-Plus 是一个…...

HalconDotNet实现OCR详解
文章目录 一、基于字符分割的 OCR二、基于模板匹配的 OCR三、基于深度学习的 OCR四、基于特征提取的 OCR五、基于区域建议的 OCR 一、基于字符分割的 OCR 字符分割是 OCR 中的一个重要步骤。首先,对包含文本的图像进行预处理,如去噪、二值化等操作&#…...

手搓一个Agent#Datawhale 组队学习Task3
书接上回,首先回顾一下Task2的一些补充: Task2主要任务是从零预训练一个tiny-llama模型,熟悉一下Llama的模型架构和流程。然后测试一下模型的效果。总的来说,因为某些未知的原因,loss一直没有降下去,导致最…...

基于SpringBoot+Vue+MySQL的在线酷听音乐系统
系统展示 用户前台界面 管理员后台界面 系统背景 随着互联网技术的飞速发展,网络已成为人们日常生活中不可或缺的一部分。在线音乐服务因其便捷性和丰富性,逐渐成为用户获取音乐内容的主要渠道。然而,传统的音乐播放平台往往存在歌曲资源有限…...

大数据实时数仓Hologres(一):Hologres 简单介绍
文章目录 Hologres 简单介绍 一、什么是实时数仓 Hologres 二、产品优势 1、专注实时场景 2、亚秒级交互式分析 3、统一数据服务出口 4、开放生态 5、MaxCompute查询加速 6、计算存储分离架构 三、应用场景 搭建实时数仓 四、产品架构 1、Shared Disk/Storage &am…...

【鸿蒙HarmonyOS NEXT】数据存储之分布式键值数据库
【鸿蒙HarmonyOS NEXT】数据存储之分布式键值数据库 一、环境说明二、分布式键值数据库介绍三、示例代码加以说明四、小结 一、环境说明 DevEco Studio 版本: API版本:以12为主 二、分布式键值数据库介绍 KVStore简介: 分布式键值数据库…...

基于springboot+小程序的儿童预防接种预约管理系统(疫苗1)(源码+sql脚本+视频导入教程+文档)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1、项目介绍 本儿童预防接种预约微信小程序可以实现管理员和用户。 1、管理员功能有个人中心,用户管理,儿童信息管理,疫苗信息管理,儿童接种管理&#x…...

计算物理精解【8】-计算原理精解【5】
文章目录 logistic模型多元回归分析多元回归分析概览1. 多元回归的概念与重要性2. 多元回归在实际应用中的例子3. 多元回归在预测和解释数据中的优势和局限性4. 多元回归的优缺点及改进建议 多元线性回归分析详解一、原理二、性质三、计算四、例子与例题五、应用场景六、优缺点…...

【Linux】 tcp | 解除服务器对tcp连接的限制 | 物联网项目配置
一、修改tcp连接限制 1、编辑 vi /etc/sysctl.conf 2、内容 net.ipv4.tcp_keepalive_intvl 75 net.ipv4.tcp_keepalive_probes 9 net.ipv4.tcp_keepalive_time 7200 net.ipv4.ip_local_port_range 1024 65535 net.ipv4.ip_conntrack_max 20000 net.ipv4.tcp_max_tw_bucket…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
