力扣9.25
2306. 公司命名
给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下:
从 ideas 中选择 2 个 不同 名字,称为 ideaA 和 ideaB 。
交换 ideaA 和 ideaB 的首字母。
如果得到的两个新名字 都 不在ideas 中,那么 ideaA ideaB(串联 ideaA 和 ideaB ,中间用一个空格分隔)是一个有效的公司名字。
否则,不是一个有效的名字。
返回 不同 且有效的公司名字的数目。
数据范围
2 <= ideas.length <= 5 * 1041 <= ideas[i].length <= 10ideas[i]由小写英文字母组成ideas中的所有字符串 互不相同
分析
将字母按开头分类,放入 v e c t o r vector vector中,预处理每个开头对应的集合中的单词在和后面的字母交换首字母后仍然合法的单词的数量,放在 c n t [ i ] [ j ] cnt[i][j] cnt[i][j]中( c n t [ i ] [ j ] cnt[i][j] cnt[i][j]表示以 i i i开头的单词集中若和字符j交换首字母后仍然合法的单词数目),外层循环遍历所有的单词,内存循环遍历字母序比当前单词首字母小的字母,若能交换,则 r e s res res加上 c n t cnt cnt对应的值。
代码
typedef long long LL;
class Solution {
public:const static int N = 35, M = 5e4 + 5;// unordered_map<string, bool> vis;unordered_set<string> st;int cnt[N][N];vector<string> idea[N];long long distinctNames(vector<string>& ideas) {for(auto v : ideas) {// vis[v] = true;st.insert(v);idea[v[0] - 'a'].push_back(v);}for(int i = 'a' - 'a'; i <= 'z' - 'a'; i ++ ) {for(int j = 'a'; j <= 'z'; j ++ ) {for(auto k : idea[i]) {string ts = k;ts[0] = j;// if(!vis[ts]) cnt[i][j - 'a'] ++ ;if(!st.count(ts)) cnt[i][j - 'a'] ++ ;}}}LL res = 0;for(int i = 'a' - 'a'; i <= 'z' - 'a'; i ++ ) {for(auto s : idea[i]) {for(int j = 0; j < i; j ++ ) {string ts = s;ts[0] = char(j + 'a');if(st.count(ts)) continue;res += cnt[j][i];}}}return res * 2;}
};
740. 删除并获得点数
给你一个整数数组 nums ,你可以对它进行一些操作。
每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
数据范围
1 <= nums.length <= 2 * 1041 <= nums[i] <= 104
分析
将每个数字出现的个数用cnt数组记录,令dp[i][0]表示不删除值为i的数获得点数最大值,dp[i][1]表示删除值为i的数获得点数最大值,状态转移如下
- d p [ i ] [ 0 ] = m a x ( d p [ i − 1 ] [ 1 ] , d p [ i − 1 ] [ 0 ] ) dp[i][0]=max(dp[i-1][1],dp[i-1][0]) dp[i][0]=max(dp[i−1][1],dp[i−1][0])
- d p [ i ] [ 1 ] = d p [ i − 1 ] [ 0 ] + c n t [ i ] ∗ i dp[i][1]=dp[i-1][0]+cnt[i]*i dp[i][1]=dp[i−1][0]+cnt[i]∗i
代码
class Solution {
public:const static int N = 1e4 + 5;int cnt[N];int dp[N][2];int n;int deleteAndEarn(vector<int>& nums) {n = nums.size();for(int i = 0; i < n; i ++ ) cnt[nums[i]] ++ ;for(int i = 1; i <= N - 5; i ++ ) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);dp[i][1] = dp[i - 1][0] + cnt[i] * i;}int res = 0;for(int i = 0; i <= N - 5; i ++ ) {res = max(res, dp[i][0]);res = max(res, dp[i][1]);}return res;}
};
120. 三角形最小路径和
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
数据范围
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-104 <= triangle[i][j] <= 104
分析
简单DP,注意在边界的情况
代码
class Solution {
public:const static int N = 205;int dp[N][N];int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size();for(int i = 0; i < n; i ++ ) {for(int j = 0; j <= i; j ++ ) {if(j == 0) dp[i + 1][j + 1] = dp[i][j + 1] + triangle[i][j]; else if(j == i) dp[i + 1][j + 1] = dp[i][j] + triangle[i][j]; else dp[i + 1][j + 1] = min(dp[i][j + 1], dp[i][j]) + triangle[i][j];}}int res = 0x3f3f3f3f;for(int i = 0; i < n; i ++ ) res = min(res, dp[n][i + 1]);return res;}
};
相关文章:

力扣9.25
2306. 公司命名 给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下: 从 ideas 中选择 2 个 不同 名字,称为 ideaA 和 ideaB 。 交换 ideaA 和 ideaB 的首字母。 如果得到的两个新名字 都 不在ideas 中,那么 …...

从零开始之AI面试小程序
从零开始之AI面试小程序 文章目录 从零开始之AI面试小程序前言一、工具列表二、开发部署流程1. VMWare安装2. Centos安装3. Centos环境配置3.1. 更改子网IP3.2. 配置静态IP地址 4. Docker和Docker Compose安装5. Docker镜像加速源配置6. 部署中间件6.1. MySQL部署6.2. Redis部署…...
Html2OpenXml:HTML转化为OpenXml的.Net库,轻松实现Html转为Word。
推荐一个开源库,轻松实现HTML转化为OpenXml。 01 项目简介 Html2OpenXml 是一个开源.Net库,旨在将简单或复杂的HTML内容转换为OpenXml组件。 该项目始于2009年,最初是为了将用户评论转换为Word文档而设计的 随着时间的推移,Ht…...

HumanNeRF:Free-viewpoint Rendering of Moving People from Monocular Video 精读
1. 姿态估计和骨架变换模块 人体姿态估计:HumanNeRF 通过已知的单目视频对视频中人物的姿态进行估计。常见的方法是通过人体姿态估计器(如 OpenPose 或 SMPL 模型)提取人物的骨架信息,获取 3D 关节的位置信息。这些关节信息可以帮…...
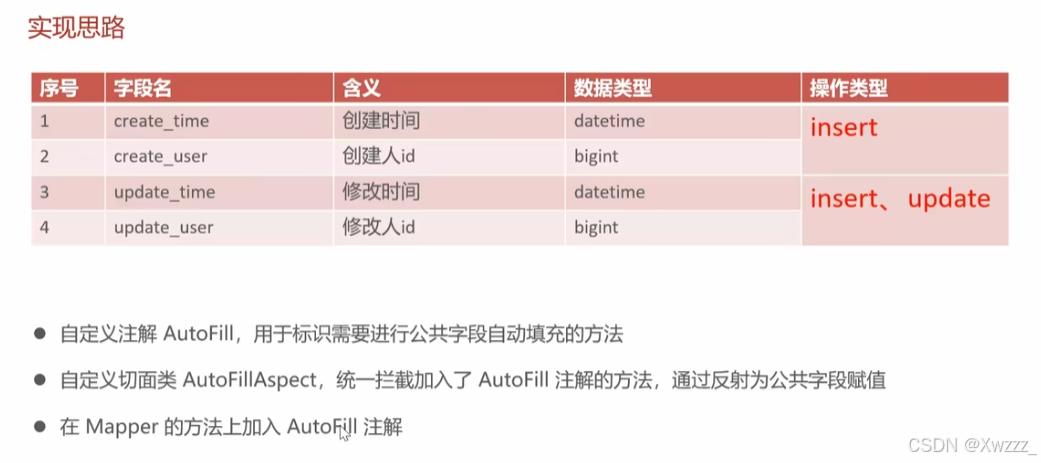
Springboot中基于注解实现公共字段自动填充
1.使用场景 当我们有大量的表需要管理公共字段,并且希望提高开发效率和确保数据一致性时,使用这种自动填充方式是很有必要的。它可以达到一下作用 统一管理数据库表中的公共字段:如创建时间、修改时间、创建人ID、修改人ID等,这些…...

Android 已经过时的方法用什么新方法替代?
过时修正举例 (Kotlin): getColor(): resources.getColor(R.color.white) //已过时// 修正后:ContextCompat.getColor(this, R.color.white) getDrawable(): resources.getDrawable(R.mipmap.test) //已过时//修正后:ContextCompat.getDrawable(this, R.mipmap.test) //…...

【RocketMQ】MQ与RocketMQ介绍
🎯 导读:本文介绍了消息队列(MQ)的基本概念及其在分布式系统中的作用,包括实现异步通信、削峰限流和应用解耦等方面的优势,并对ActiveMQ、RabbitMQ、RocketMQ及Kafka四种MQ产品进行了对比分析,涵…...
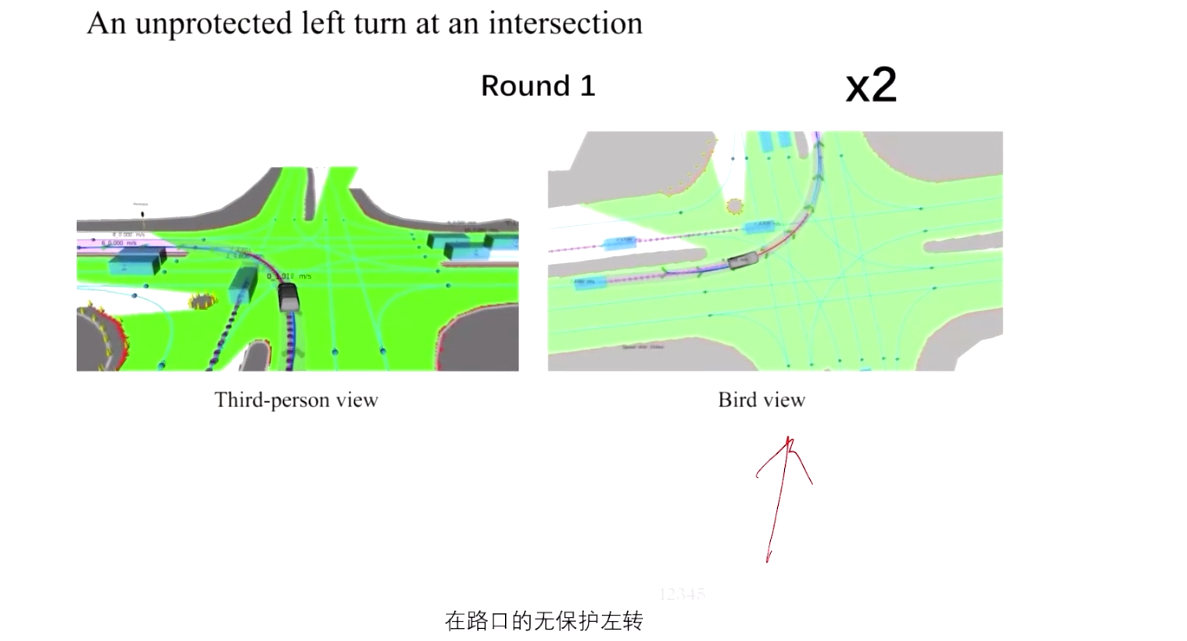
【笔记】自动驾驶预测与决策规划_Part4_时空联合规划
文章目录 0. 前言1. 时空联合规划的基本概念1.1 时空分离方法1.2 时空联合方法 2.基于搜索的时空联合规划 (Hybrid A* )2.1 基于Hybrid A* 的时空联合规划建模2.2 构建三维时空联合地图2.3 基于Hybrid A*的时空节点扩展2.4 Hybrid A* :时空节…...

Linux指令收集
文件和目录操作 ls: 列出目录内容。 -l 显示详细信息。-a 显示隐藏文件(以.开头的文件)。cd: 改变当前工作目录。 cd ~ 返回主目录。cd .. 上移一级目录。pwd: 显示当前工作目录。mkdir: 创建目录。 mkdir -p path/to/directory 创建多级目录。rmdir: 删…...
)
《C++并发编程实战》笔记(五)
五、内存模型和原子操作 5.1 C中的标准原子类型 原子操作是不可分割的操作,它或者完全做好,或者完全没做。 标准原子类型的定义在头文件<atomic>中,类模板std::atomic<T>接受各种类型的模板实参,从而创建该类型对应…...
)
在Python中实现多目标优化问题(5)
在Python中实现多目标优化问题 在Python中实现多目标优化,除了传统的进化算法(如NSGA-II、MOEA/D)和机器学习辅助的方法之外,还有一些新的方法和技术。以下是一些较新的或较少被提及的方法: 1. 基于梯度的多目标优化…...
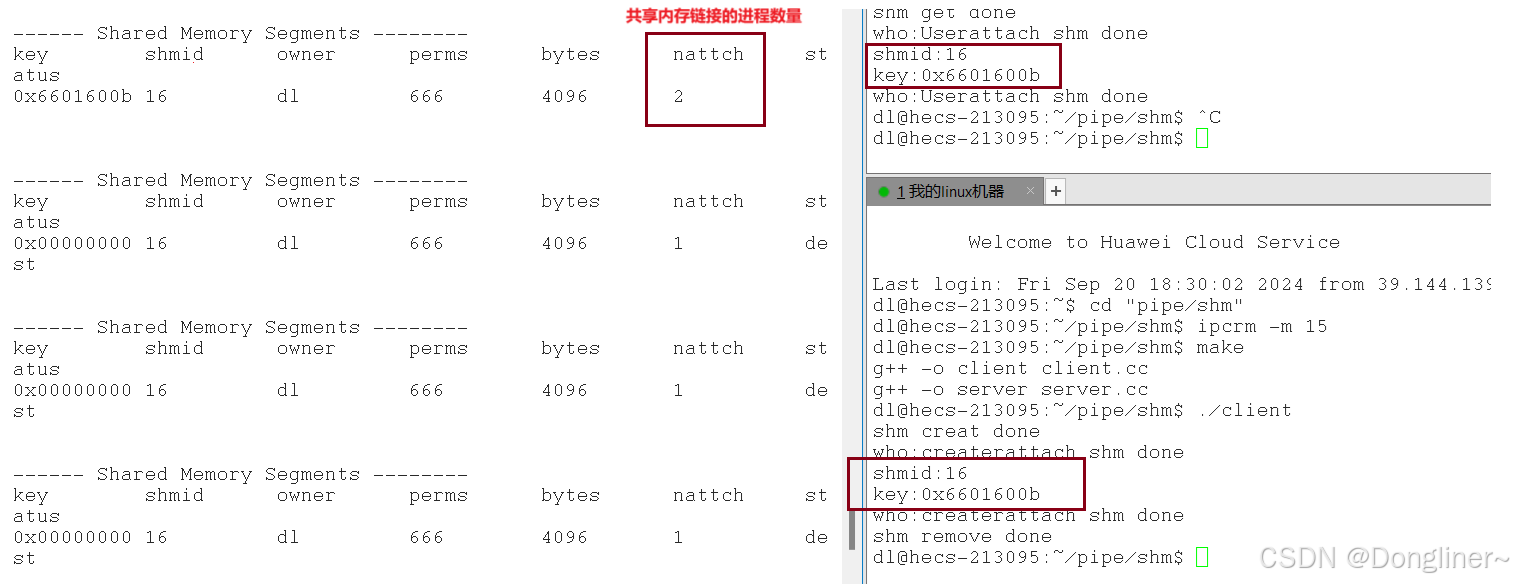
【Linux:共享内存】
共享内存的概念: 操作系统通过页表将共享内存的起始虚拟地址映射到当前进程的地址空间中共享内存是由需要通信的双方进程之一来创建但该资源并不属于创建它的进程,而属于操作系统 共享内存可以在系统中存在多份,供不同个数,不同进…...

今年Java回暖了吗
今年回暖了吗 仅结合师兄和同学的情况 BG 大多双非本 少部分211本 985硕 去年十月一之前 基本转正都失败 十月一之前0 offer 只有很少的人拿到美团 今年十月一之前 有HC的基本都转正了(美团、字节等),目前没有HC的说也有机会(…...

a = Sw,其中a和w是向量,S是矩阵,求w等于什么?w可以写成关于a和S的什么样子的公式
给定公式: a S w a S w aSw 其中: a a a 是已知向量, S S S 是已知矩阵, w w w 是未知向量。 我们的目标是求解 w w w,即将 w w w 表示为 a a a 和 S S S 的函数。 情况 1:矩阵 S S S 可逆 如果矩…...

多线程事务管理:Spring Boot 实现全局事务回滚
多线程事务管理:Spring Boot 实现全局事务回滚 在日常开发中,我们常常会遇到需要在多线程环境下进行数据库操作的场景。这类操作的挑战在于如何保证多个线程中的数据库操作要么一起成功,要么一起失败,即 事务的原子性。尤其是在多个线程并发执行的情况下,确保事务的一致性…...
Vue3 中集成海康 H5 监控视频播放功能
🌈个人主页:前端青山 🔥系列专栏:Vue篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来Vuet篇专栏内容:Vue-集成海康 H5 监控视频播放功能 目录 一、引言 二、环境搭建 三、代码解析 子组件部分 1.…...

Linux: eBPF: libbpf-bootstrap-master 编译
文章目录 简介编译运行展示输出展示:简介 这个是使用libbpf的一个例子; 编译 如果是一个可以联网的机器,这个libbpf-bootstrap的编译就方便了,完全是自动化的下载依赖文件;如果没有,就只能自己准备这些个软件。 需要:libbpf-static; [root@RH8-LCP c]# makeLIB …...
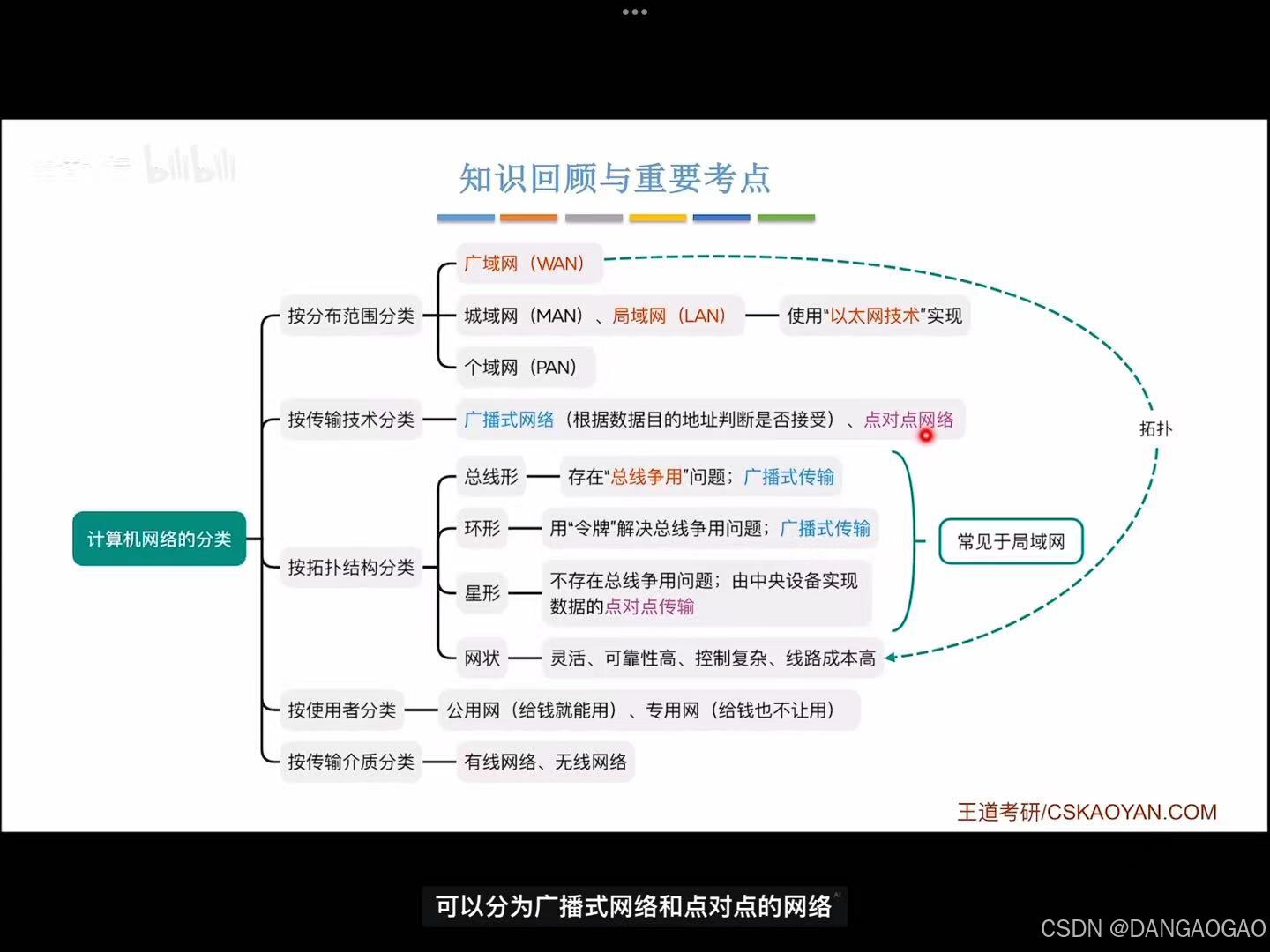
1.1.4 计算机网络的分类
按分布范围分类: 广域网(wan) 城域网(man) 局域网(lan) 个域网(pan) 注意:如今局域网几乎采用“以太网技术实现”,因此“以太网”几乎成了“局域…...

周家庄智慧旅游小程序
项目概述 周家庄智慧旅游小程序将通过数字化手段提升游客的旅游体验,依托周家庄的自然与文化资源,打造智慧旅游新模式。该小程序将结合虚拟现实(VR)、增强现实(AR)和人工智能等技术,提供丰富的…...

【在Linux世界中追寻伟大的One Piece】命名管道
目录 1 -> 命名管道 1.1 -> 创建一个命名管道 1.2 -> 匿名管道与命名管道的区别 1.3 -> 命名管道的打开规则 1.4 -> 例子 1 -> 命名管道 管道应用的一个限制就是只能在具有共同祖先(具有亲缘关系)的进程间通信。如果我们想在不相关的进程之间交换数据&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
