在Python中实现多目标优化问题(6)
在Python中实现多目标优化问题
在Python中实现多目标优化,除了传统的进化算法(如NSGA-II、MOEA/D)和一些基于机器学习的方法外,还有一些新的方法和技术。这些新方法通常结合了最新的研究成果,提供了更高效的解决方案。以下是几种较新的或较少被提及的多目标优化方法:
1. 使用Optuna进行多目标贝叶斯优化
Optuna是一个自动超参数优化框架,支持多目标优化。它通过贝叶斯优化来寻找帕累托最优解。
首先安装Optuna:
pip install optuna
然后,可以定义一个多目标优化问题并使用Optuna进行优化。
示例:使用Optuna进行多目标优化
import optuna# 定义目标函数
def objective(trial):x = trial.suggest_uniform('x', -2, 2)y = trial.suggest_uniform('y', -2, 2)f1 = x**2 + y**2f2 = (x - 1)**2 + y**2return f1, f2# 创建一个研究对象
study = optuna.create_study(directions=["minimize", "minimize"])# 运行优化
study.optimize(objective, n_trials=100)# 打印结果
for trial in study.best_trials:print(f"Trial: {trial.number}")print(f" X: {trial.params['x']}, {trial.params['y']}")print(f" F: {trial.values[0]}, {trial.values[1]}")
2. 使用PyGMO库进行多目标优化
PyGMO是一个用于全局优化的Python库,支持多种多目标优化算法,包括NSGA-II、MOEA/D等。
首先安装PyGMO:
pip install pygmo
然后,可以定义一个多目标优化问题并使用PyGMO进行优化。
示例:使用PyGMO进行多目标优化
import pygmo as pg
import numpy as np# 定义目标函数
def multi_objective_function(x):f1 = x[0]**2 + x[1]**2f2 = (x[0] - 1)**2 + x[1]**2return [f1, f2]# 定义问题
udp = pg.problem(pg.cec2009(1, dim=2)) # 使用CEC2009基准问题
udp._objfun = multi_objective_function # 替换为自定义的目标函数
udp._nobj = 2 # 设置目标函数数量# 初始化优化器
algo = pg.algorithm(pg.nsga2(gen=100))
pop = pg.population(udp, size=100)# 运行优化
pop = algo.evolve(pop)# 打印结果
for ind in pop.get_x():print(f"X: {ind}, F: {multi_objective_function(ind)}")
3. 使用JMetalPy库进行多目标优化
JMetalPy是一个用于多目标优化的Python库,支持多种多目标优化算法,包括NSGA-II、SPEA2等。
首先安装JMetalPy:
pip install jmetalpy
然后,可以定义一个多目标优化问题并使用JMetalPy进行优化。
示例:使用JMetalPy进行多目标优化
from jmetal.algorithm.multiobjective.nsgaii import NSGAII
from jmetal.operator import SBXCrossover, PolynomialMutation
from jmetal.problem import ZDT1
from jmetal.util.termination_criterion import StoppingByEvaluations
from jmetal.core.solution import FloatSolution
from jmetal.util.solution import get_non_dominated_solutions
import numpy as np# 定义目标函数
class MyProblem(ZDT1):def __init__(self, number_of_variables: int = 2):super(MyProblem, self).__init__(number_of_variables)self.obj_directions = [self.MINIMIZE, self.MINIMIZE]self.obj_labels = ['f1', 'f2']def evaluate(self, solution: FloatSolution) -> FloatSolution:x1 = solution.variables[0]x2 = solution.variables[1]solution.objectives[0] = x1**2 + x2**2solution.objectives[1] = (x1 - 1)**2 + x2**2return solution# 创建问题实例
problem = MyProblem()# 定义遗传操作
max_evaluations = 10000
algorithm = NSGAII(problem=problem,population_size=100,offspring_population_size=100,mutation=PolynomialMutation(probability=1.0 / problem.number_of_variables, distribution_index=20),crossover=SBXCrossover(probability=1.0, distribution_index=20),termination_criterion=StoppingByEvaluations(max=max_evaluations)
)# 运行优化
algorithm.run()# 获取非支配解
solutions = algorithm.get_result()
front = get_non_dominated_solutions(solutions)# 打印结果
for solution in front:print(f"X: {solution.variables}, F: {solution.objectives}")
4. 使用Platypus库进行多目标优化
Platypus是一个用于多目标优化的Python库,支持多种多目标优化算法,包括NSGA-II、NSGA-III等。
首先安装Platypus:
pip install platypus-opt
然后,可以定义一个多目标优化问题并使用Platypus进行优化。
示例:使用Platypus进行多目标优化
from platypus import NSGAII, Problem, Real# 定义问题
class MyProblem(Problem):def __init__(self):super(MyProblem, self).__init__(2, 2) # 2个决策变量,2个目标self.types[:] = [Real(-2, 2), Real(-2, 2)] # 决策变量的范围self.directions[:] = [Problem.MINIMIZE, Problem.MINIMIZE] # 两个目标都是最小化def evaluate(self, solution):x = solution.variables[0]y = solution.variables[1]solution.objectives[:] = [x**2 + y**2, (x - 1)**2 + y**2]# 创建问题实例
problem = MyProblem()# 初始化遗传算法
algorithm = NSGAII(problem)# 运行算法
algorithm.run(10000) # 进行10000次迭代# 打印结果
for solution in algorithm.result:print(f"X: {solution.variables}, F: {solution.objectives}")
5. 使用Pymoo的新特性
pymoo库不断更新,引入了许多新特性和改进。例如,最近版本的pymoo支持更多的算法和更好的可视化工具。
示例:使用pymoo的最新特性
import numpy as np
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.core.problem import Problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter# 定义问题
class MyProblem(Problem):def __init__(self):super().__init__(n_var=2, # 决策变量的数量n_obj=2, # 目标函数的数量xl=np.array([-2, -2]), # 决策变量的下界xu=np.array([2, 2]) # 决策变量的上界)def _evaluate(self, x, out, *args, **kwargs):f1 = x[:, 0]**2 + x[:, 1]**2f2 = (x[:, 0] - 1)**2 + x[:, 1]**2out["F"] = np.column_stack([f1, f2])# 创建问题实例
problem = MyProblem()# 初始化遗传算法
algorithm = NSGA2(pop_size=100)# 运行最小化过程
res = minimize(problem,algorithm,('n_gen', 100), # 进化代数seed=1, # 随机种子verbose=False # 不打印迭代信息
)# 可视化结果
plot = Scatter()
plot.add(res.F)
plot.show()# 打印结果
print("Best solutions found: \nX = %s\nF = %s" % (res.X, res.F))
这些方法展示了如何利用现代技术如贝叶斯优化、差分进化、粒子群优化以及最新的多目标优化库来解决多目标优化问题。选择哪种方法取决于你的具体需求和问题的复杂性。每种方法都有其优缺点,你可以根据实际情况进行选择。
相关文章:
)
在Python中实现多目标优化问题(6)
在Python中实现多目标优化问题 在Python中实现多目标优化,除了传统的进化算法(如NSGA-II、MOEA/D)和一些基于机器学习的方法外,还有一些新的方法和技术。这些新方法通常结合了最新的研究成果,提供了更高效的解决方案。…...

Java EE中的编码问题及解决方案
Java EE中的编码问题及解决方案 在Java EE开发中,处理字符编码是确保数据正确传输和显示的重要环节。不同的编码不一致会导致乱码,影响用户体验。本文将总结在Java EE中可能遇到的编码问题及其解决方案。 1. 输入数据编码问题 在表单提交时,…...

9月27日,每日信息差
第一、中国科学家团队在干细胞治疗领域取得重要突破,通过化学重编程技术成功制备出胰岛细胞,并用于移植治疗一名 1 型糖尿病患者,实现了临床功能性治愈。相关研究成果已发表在国际权威期刊《细胞》上。 第二、交通运输部公路局局长周荣峰在国…...

什么是 Angular 开发中的 Dumb components
Dumb components,在 Angular 开发中也被称为 Presentational components,它们的主要职责是通过展示数据和触发事件,把业务逻辑和 UI 表现分离开来。Dumb components 只通过 Input() 接收数据,Output() 向外发送事件,不…...

Docker 进入容器运行命令的详细指南
Docker 进入容器运行命令的详细指南 Docker 是一个开源的容器化平台,广泛应用于开发和生产环境中。它允许开发者打包应用程序及其依赖项到容器中,并能够在不同的平台上快速部署和运行。容器通常是独立且隔离的,但在开发、调试或维护过程中&a…...

如何禁止非真实用户的ip访问网站服务器
为了禁止非真实用户的IP访问网站服务器,可以采用多种技术手段和策略。以下是一些常用的方法: 1. 使用IP黑名单和白名单 黑名单:定期更新和维护一个IP黑名单,阻止已知的恶意IP地址或数据中心IP访问网站。白名单:对于特…...

探索SpringBoot:学科竞赛管理项目开发
2 相关技术简介 2.1Java技术 Java是一种非常常用的编程语言,在全球编程语言排行版上总是前三。在方兴未艾的计算机技术发展历程中,Java的身影无处不在,并且拥有旺盛的生命力。Java的跨平台能力十分强大,只需一次编译,任…...

ultralytics yolo v8 示例:加载官方模型进行推理
Ultralytics YOLO 是计算机视觉和 ML 领域专业人士的高效工具。 安装 ultralytics 库: pip install ultralytics 实现代码如下: import cv2 from ultralytics import YOLO# 加载预训练的 YOLOv8n 模型 ckpt_dir "./ckpt/" # 模型缓存地址…...

【中间件学习】Nginx快速入门(为了配置一个项目)
-----------------------------本文章借鉴遇见狂神说--------------------------- 一、一个产品出现瓶颈?? 在一个产品刚刚上线的时候,并发量小,用户使用的少,所以在低并发的情况下,一个jar包启动应该就够…...

鸿蒙harmonyos next flutter通信之MethodChannel获取设备信息
本文将通过MethodChannel获取设备信息,以此来演练MethodChannel用法。 建立channel flutter代码: MethodChannel methodChannel MethodChannel("com.xmg.test"); ohos代码: private channel: MethodChannel | null nullthis.c…...
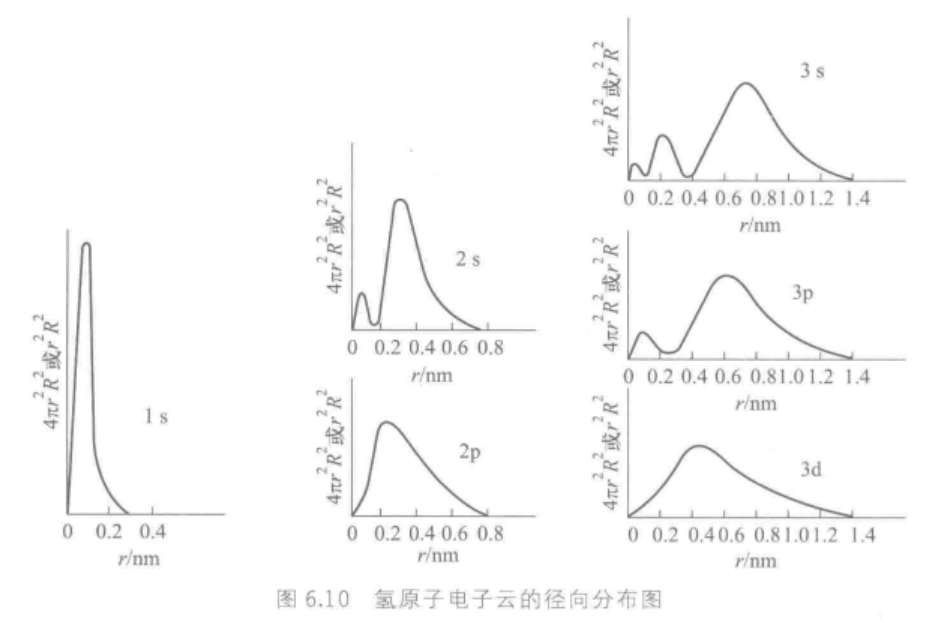
【笔记】原子结构的近代理论
近代原子结构理论的建立是从氢原子光谱得到启示的。 一、氢原子光谱与波尔理论 1.氢原子光谱 在装有两个电极的真空玻璃管内通入极少量高纯氢气,通高压电使之放电,管中发出的光束通过分光棱镜,得到分立的谱线,称为线状光谱。 发…...

【python】循环中断:break 和 continue
目录: while 循环的基础语法while 循环的基础案例while 循环的嵌套应用while 循环的嵌套案例for 循环的基础语法for 循环的嵌套应用循环中断:break 和 continue综合案例 学习目标: 掌握使用 continue 和 break 关键字控制循环 思考&#…...

WIFI密码默认显示
文章目录 需求分析遇到问题问题原因解决方案 需求 在进入设置,点击某一个wifi,连接wifi 界面,显示密码默认选中状态,效果如下 分析 在 WiFi密码被输入法挡住 中我们已经分析了整个流程,布局文件和控制中心。 结局系统设置WIFI连…...

Emiya 家今天的饭C++
题目: 样例解释: 【样例 1 解释】 由于在这个样例中,对于每组 i,j,Emiya 都最多只会做一道菜,因此我们直接通过给出烹饪方法、主要食材的编号来描述一道菜。 符合要求的方案包括: 做一道用烹饪方法 1、主要…...

Mybatis缓存机制(图文并茂!)
目录 一级缓存 需求我们在一个测试中通过ID两次查询Monster表中的信息。 二级缓存 案例分许(和上述一样的需求) EhCache第三方缓存 在了解缓存机制之前,我们要先了解什么是缓存: 缓存是一种高速存储器,用于暂时存储访问频繁的数据&…...

Git 工作区、暂存区和版本库
Git 工作区、暂存区和版本库 Git 是一个强大的版本控制系统,它帮助开发者管理代码历史,协作开发,以及跟踪和合并更改。为了更好地理解 Git 的工作流程,我们需要了解 Git 中的三个核心概念:工作区(Workspac…...

SSH 远程连接到 Linux 服务器上的 SQLite
通过 SSH 远程连接到 Linux 服务器上的 SQLite 数据库文件的流程,可以分为以下几个步骤: 通过 SSH 连接到远程 Linux 服务器。在远程服务器上执行 SQLite 命令行工具,操作数据库文件。在本地使用工具,通过 SSH 隧道间接访问远程的…...

使用ElasticSearch-dump工具进行ES数据迁移、备份
elasticsearch-dump基本使用 该工具基于第三方Elasticdump工具来实现,仓库地址:https://github.com/elasticsearch-dump/elasticsearch-dump/tree/master,用于更加快捷方便的将Elasticsearch不同集群的数据进行索引备份和还原。 一、安装 …...

SpringMVC源码-SpringMVC源码请求执行流程及重点方法doDispatch讲解
一、开始请求 在浏览器访问http://localhost:8080/spring_mymvc/userlist这个接口,是个get请求。 FrameworkServlet类的service方法会被请求到: 调用路径如下: service:945, FrameworkServlet (org.springframework.web.servlet) service:764, HttpSer…...

《深度学习》OpenCV 指纹验证、识别
目录 一、指纹验证 1、什么是指纹验证 2、步骤 1)图像采集 2)图像预处理 3)特征提取 4)特征匹配 5)相似度比较 6)结果输出 二、案例实现 1、完整代码 2、实现结果 调试模式: 三、…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
