集合论(ZFC)之良创关系(Well-Founded Relation)
定义在集合S中的一个二元关系(Binary Relation)记,<,有(S,<)。如果对于集合S的任意非空子集,都存在关系(<)下的最小元素,那么该关系(<)成为良创关系(Well_Founded Relation),集合S与关系(<),即(S,<),称为良创集。亦:
(s ⊂ S ∧ s ≠ ∅ → (a ∈ s → ¬(∃x∈s.(x < a)))) → Well_Founded(S)
可证,良序集(Well-Ordered Set)满足良创集的条件。即良序集为良创集。
另外,给定义一个良创集(S,<),可定义关系(<)的高度(height),同时,赋予集合S中的每个元素 x 一个序数,称该序数为对应元素 x 的关系(<)层级 ( Rank of x in < )。
那么,把这赋级规则看作是一函数 rank: S → Ordinal,其定义为
rank(x) = sup { rank(y) + 1: y < x } ( x ∈ S )
该函数 rank 是唯一存在的。其证明可通过对层级进行归纳,定义各层级集合,如
S₀ = ∅ ;
Sₙ₊₁ = {s ∈ S: ∀t(t < s → t ∈ Sₙ)};
Sₐ = ⋃ ᵢ<ₐ Sᵢ ( a 是极限序数(limit ordinal))
那么,有 S₀ ⊂ S₁ ⊂ ... ⊂ S。
令,r 为该集合的最高层级,有 Sᵣ = S。
如果 Sᵣ ≠ S,那么,(S - Sᵣ)⊂ S,而S为良创集,由此存在一个元素 a 是(S - Sᵣ)中,关系(<)下的最小元素,那么根据上述描述,a 存在于 Sᵣ₊₁ 中,与定义不符,因此,Sᵣ = S。
其中 r 为 良创集(S,<)的高度。
相关文章:
之良创关系(Well-Founded Relation))
集合论(ZFC)之良创关系(Well-Founded Relation)
定义在集合S中的一个二元关系(Binary Relation)记,<,有(S,<)。如果对于集合S的任意非空子集,都存在关系(<)下的最小元素,那么该关系&…...

centos 安装达梦数据库
一、环境准备 1.1、确认操作系统的版本和数据库的版本是否一致 ## 查看系统版本:cat /etc/redhat-release CentOS Linux release 7.5.1804 (Core)1.2、关闭防火墙和Selinux # 查看selinux是不是disabled / enforce cat /etc/selinux/config## 查看防火墙状态 fir…...

《Windows PE》6.4.1 无 DLL远程注入
本节我们将演示如何实现远程注入的两种不同方案。方案一选择远程注入代码和数据,方案二选择远程注入DLL。 本节必须掌握的知识点: 无DLL远程注入 远程注入DLL 6.4.1 无DLL远程注入 实验四十五:无DLL远程注入(C语言实现…...

浙大数据结构:10-排序6 Sort with Swap(0, i)
这道题用了数环的思想,MOOC最后视频中也有相关介绍,思想还是很巧妙的 机翻 1、思想 2、 主函数 先把数据存进来,然后从头开始遍历,如果该位置数不对则anwser,然后遍历整个环,一直加anwser,如…...

基于vue框架的的爱心捐赠物资信息系统85gsu(程序+源码+数据库+调试部署+开发环境)系统界面在最后面。
系统程序文件列表 项目功能:用户,爱心项目,捐赠类型,捐赠,积分兑换,兑换,捐赠名录,捐赠去向 开题报告内容 基于Vue框架的爱心捐赠物资信息系统开题报告 一、研究背景与意义 随着社会的发展和人们生活水平的提高,爱心捐赠活动逐渐成为连接捐赠者与受赠…...

AI对抗AI:如何应对自动化攻击新时代?
在当今这个生成式AI迅猛发展的时代,自动化攻击的威胁日益加剧。 在人工智能浪潮下,如何利用AI对抗AI,从而实现全方位的网络安全防护? 一、AI浪潮下,自动化攻击加剧 AI技术的发展既带来了前所未有的挑战,也…...

【微服务】微服务注册:构建灵活的服务管理机制
目录 引言一、什么是微服务注册?1.1 服务注册中心的作用1.2 服务注册中心的工作原理1.3 示意图 二、常见的微服务注册中心2.1 各注册中心详细对比 三、微服务注册的实现方式3.1 Spring Cloud Netflix Eureka3.2 Consul3.3 Zookeeper3.4 etcd 四、微服务注册的注意事…...

AsyncTask的工作原理和缺陷
AsyncTask的工作原理及其缺陷 AsyncTask是Android平台提供的一个轻量级的异步任务类,它允许开发者在后台线程中执行耗时操作,并在操作完成后将结果回调到主线程以更新UI。AsyncTask内部封装了线程池和Handler机制,简化了多线程编程的复杂性。…...

【React】事件绑定的方式
1. 内联函数绑定 这是最简单直接的方式,即在 JSX 语法中直接传递一个内联函数。这种方式每次渲染时都会创建新的函数实例,可能会导致不必要的性能开销。 class MyComponent extends React.Component {render() {return (<button onClick{() > th…...

Android ImageView scaleType使用
目录 一、src设置图片资源 二、scaleType设置图片缩放类型 三、scaleType具体表现 matrix: fitXY: fitStart: fitCenter: fitEnd: Center: centerCrop: centerInside: 控制ImageView和图片的大小保持一致…...

【PhpSpreadsheet】ThinkPHP5+PhpSpreadsheet实现批量导出数据
目录 前言 一、安装 二、API使用 三、完整实例 四、效果图 前言 为什么使用PhpSpreadsheet? 由于PHPExcel不再维护,所以建议使用PhpSpreadsheet来导出exlcel,但是PhpSpreadsheet由于是个新的类库,所以只支持PHP7.1及以上的版…...

Python剪辑视频
import os from moviepy.editor import VideoFileClipvideo_dir r"E:\学习\视频剪辑" s_video_file "1.mp4" d_video_file "剪辑片段1.mp4" s_video_path os.path.join(video_dir, s_video_file) # 原视频文件路径 d_video_path os.path…...
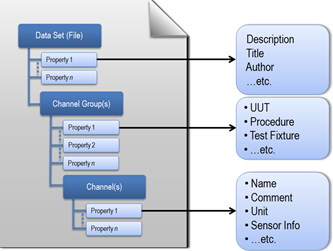
LabVIEW提高开发效率技巧----高效文件I/O
在LabVIEW开发中,文件I/O操作常常是性能瓶颈之一,特别是处理大数据时,如何高效地存储和读取数据显得尤为重要。本文将详细介绍如何利用TDMS Streaming来实现高效的文件I/O,并结合具体例子说明在实际开发中的应用技巧。 1. 什么是T…...

影刀RPA接口_查询应用主流程参数结构
影刀接口_查询应用主流程参数结构 链接 import requests from time import sleepaccessKeyId"XXX" accessKeySecret"XXX"#1.获取token def get_access_token():url"https://api.yingdao.com/oapi/token/v2/token/create"headers{"Content…...

2d实时数字人聊天语音对话使用案例,对接大模型
参看: https://github.com/wan-h/awesome-digital-human-live2d 电脑环境: ubuntu 1060ti 下载: git clone https://github.com/wan-h/awesome-digital-human-live2d.gitdocker部署; cd awesome-digital-human-live2d docker-compose -f docker-compose-quickStart.ya…...

LeetCode | 69.x的平方根
这道题很适合用二分来解决,算是二门入门的一个练手题吧思想就是首先设置两个指针,一个是0,一个是x,相当于在数轴上划定一个区域 [ 0 , x ]然后计算数轴中间值和我们想要找的值的大小关系,因为数轴是有序的,…...
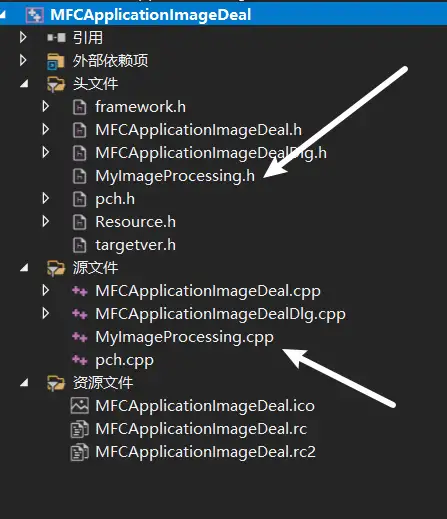
使用Windows创建一个MFC应用【带界面】
MFC使用教程【对初学者保姆型友好!】 目录 前提条件 1:创建MFC应用程序 2. 项目结构解读 引用 外部依赖项 头文件 源文件 资源文件 文件功能详解 项目的主要流程 步骤2:配置OpenCV 安装OpenCV 包含目录与库文件 步骤3࿱…...

springboot整合lombok
只需要引入lombok依赖 <dependency> <groupId>org.projectlombok</groupId> <artifactId>lombok</artifactId> <version>1.16.18</version></dependency> 然后application.yml配置文件中加上 logging: level: …...
使用Arcgis批量自动出图
操作方法如下: 1 2 3 4 5 6 7 设置好选项,开始打印。 8 生成pdf。 第一步:shp放到数据库中,标注转注记,然后编辑注记,符号样式设置好。准备出图:(转注记时候尽量压盖监测等选最…...

Web Worker加载外部文件实践
概述 在Web Worker 多线程编程一文中介绍了Web Worker的编程思想,碰巧最近工作中某个工程需要加载外部文件,最大的文件大小达到30MB,Web Worker无疑是不错的选择。 编程实现 不用 Web Worker 加载外部文件使用原生的fetch方法读取文件,其核心代码如下: function loadland…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
