数据结构 - 堆
今天我们将学习新的数据结构-堆。

01定义
堆是一种特殊的二叉树,并且满足以下两个特性:
(1)堆是一棵完全二叉树;
(2)堆中任意一个节点元素值都小于等于(或大于等于)左右子树中所有节点元素值;
小根堆,根节点元素永远是最小值,即堆中每个节点元素值都小于等于左右子树中所有节点元素值;
大根堆,根节点元素永远是最大值,即堆中每个节点元素值都大于等于左右子树中所有节点元素值;

根据堆的定义我们不难发现,堆特别适合用来求集合最值,以及求最值引申的问题比如:排序、优先队列、动态排名等等
02结构
我们指定堆是一种特殊完全二叉树,因此堆的逻辑结构是树。
我们指定树的存储结构有两种,顺序存储(数组)和链式存储(链表),那么堆的存储结构是什么呢?
既然堆是完全二叉树,那么树的存储结构当然也适用于堆。但是堆一般都选用顺序存储(数组)实现。其原因有三:
(1)位置计算简单:数组实现堆可以使用完全二叉树特性用简单的数学公式即可表示父子节点的索引关系,从而避免了链表实现使用额外的指针,即减少内存开销和实现复杂度;
(2)性能好:数组的连续内存特性使得其有高效的访问速度,而链表因为节点不一定连续访问速度相对较差;
(3)操作简单:数组实现在逻辑实现上更加简单高效,通过交换数组中的元素即可快速实现堆的性质,链表实现在插入和删除操作中需要遍历链表效率远不如数组实现;
总结一句话数组简单、内存连续、性能更好,所以一般选用数组实现堆,当然不一般的情况也可以使用链表实现。
03实现(最小堆)
下面我们就用数组来实现一个最小堆结构,最大堆只是比较大小不同这里就不做过多赘述。
1、初始化 Init
首先我们需要定义两个私有变量,一个变量用来存放堆元素的数组,一个变量用来存放数组尾元素索引,主要用来跟踪当前堆元素个数情况。
而初始化方法就是初始化两个变量,创建指定容量数组,以及标记数组尾元素索引为-1,表示堆中还没有元素。
//存放堆元素
private int[] _array;
//数组尾元素索引
private int _tailIndex;
//初始化堆为指定容量
public MyselfMinHeap Init(int capacity)
{//初始化指定长度数组用于存放堆元素_array = new int[capacity];//初始化数组尾元素索引为-1,表示空数组_tailIndex = -1;//返回堆return this;
}
2、获取堆容量 Capacity
堆容量指的是数组的固定空间,即数组最多能容纳多少个元素,直接返回数组长度即可。
//堆容量
public int Capacity
{get{return _array.Length;}
}
3、获取堆元素数量 Count
堆元素数量指当前堆中一共有多少个元素,我们可以通过私有字段数组尾元素索引值加1获得。
//堆元素数量
public int Count
{get{//数组尾元素索引加1即为堆元素数量return _tailIndex + 1;}
}
4、获取堆顶元素 Top
堆顶元素指树节点中的根节点,也就是数组中的第一个元素。同时要注意判断数组是否为空,为空报异常。
//获取堆顶元素,即最小元素
public int Top
{get{if (IsEmpty()){//空堆,不可以进行获取最小堆元素操作throw new InvalidOperationException("空堆");}return _array[0];}
}
5、是否为空堆 IsEmpty
空堆即堆中还没有任何元素,当数组尾元素索引为-1时表示空堆。
//检查堆是否为空
public bool IsEmpty()
{return _tailIndex == -1;
}
6、是否为满堆 IsFull
满堆即堆空间已满不能再添加新元素,当数组尾元素索引等于数组容量减1时表示满堆。
//检查堆是否为满堆
public bool IsFull()
{//数组末尾元素索引等于数组容量减1表示满堆return _tailIndex == _array.Length - 1;
}
7、入堆 Push
入堆即向堆中新添加一个元素。
而入堆也涉及到一个问题,就是如何保存每次添加完新元素后,还保持着堆的特性。很显然我们也没办法做到直接把新元素直接插入到其正确的位置上,因此我们可以梳理新添加一个元素的流程,可能大致有以下几个步骤:
(1)首先把新元素添加到堆的末尾;
(2)然后调整堆使其满足堆的性质;
(3)更新堆尾元素索引;
而难点显然就在第二步,如何调整数组使其满足堆的性质?
我们先直接模拟把7654按顺序推入堆中,看看如何实现。
(1)首先7入堆,此时只有一个元素,无需做任何操作,而7就作为根节点;
(2)然后6入堆,此时已有两个元素,因此需要保持堆的两个特性:根节点永远是最小元素和堆是完全二叉树。由完全二叉树特性可得,根节点左子节点索引为20+1=1,而右子节点索引为20+2=2,而此时6的索引为1,所以6为左子节点;又因6比7小,所以根节点变为6, 7变为根节点的左子节点;

(3)然后5入堆,此时已有3个元素,所以5的索引为2,而根节点右子节点索引为2*0+2=2,所以5添加为根节点的右子节点。5比6小,所以5和6交互位置;

(4)然后4入堆,此时已有4个元素,所以4的索引为3,而7节点左子节点索引为2*1+1=3,所以4添加为7节点的左子节点。4比7小,所以4和7交互位置; 再次比较4和5,4比5小,所以4和5交互位置;

相信到这里大家已经看出一点规律了,调整整个数组元素使其满足堆的性质的整个过程大致分为以下几个步骤:
(1)从新元素开始向上比较其与父节点元素的值大小;
(2)如果新元素值小于其父节点元素值,则交互两者位置,否则结束调整;
(3)重复以上步骤直至处理到根节点。
代码实现如下:
//入堆 向堆中添加一个元素
public void Push(int data)
{if (IsFull()){//满堆,不可以进行入添加元素操作throw new InvalidOperationException("满堆");}//新元素索引var index = _tailIndex + 1;//在数组末尾添加新元素_array[index] = data;//向上调整堆,以保持堆的性质SiftUp(index);//尾元素索引向后前进1位_tailIndex++;
}
//向上调整堆,以保持堆的性质
private void SiftUp(int index)
{//一直调整到堆顶为止while (index > 0){//计算父节点元素索引var parentIndex = (index - 1) / 2;//如果当前元素大于等于其父节点元素,则结束调整if (_array[index] >= _array[parentIndex]){break;}//否则,交换两个元素(_array[parentIndex], _array[index]) = (_array[index], _array[parentIndex]);//更新当前索引为父节点元素索引继续调整index = parentIndex;}
}
8、出堆 Pop
出堆即删除并返回堆顶元素(堆中最小元素)。
而出堆同样也涉及到和入堆同样的问题,就是如何保存每次删除元素后,还保持着堆的特性。
显然删除和添加元素情况还不一样。添加新元素后还是一棵完全二叉树,只不过可能没有满足堆的性质,所以需要调整。而删除就不一样了,想象一下当我们把堆顶元素删除后,回怎样?根节点空了,此时还能较完全二叉树吗?显然不能。
如何处理呢?直观的想法就是根节点空了就用其子节点补充上呗,就这样从上到下一直填补,直至最后的空落在了叶子节点那一层,如果这个空位落到了叶子节点左侧,而右侧还有值,此时就表明堆不满足完全二叉树这一特性,因此还需要把这个空位移到堆的末尾,想象都头大。这显然不是一个好办法。
既然我们最后要把根节点删除后的这个空位移到堆的末尾,何不直接把这个空位和堆的尾元素直接调换个位置呢,然后再参考出堆中调整整个数组使其满足堆的性质。
我们梳理整个流程,可能大致有以下几个步骤:
(1)首先获取堆顶元素并暂存;
(2)将堆尾元素赋值给堆顶元素,并将堆尾元素置空;
(3)然后调整堆使其满足堆性质;
(4)更新数组尾元素索引,并返回暂存的堆顶元素;
而难点同样在第二步,如何调整数组使其满足堆的性质?入堆是新元素在堆尾所以是从下往上进行调整,而出堆是堆顶元素需要调整是否可以从上往下进行调整呢?
我们把87654按顺序推入堆中后把4推出堆中,看看如何实现。
首先删除根节点4,并把堆尾元素8放到根节点;
为了保持堆特性,找出根节点及其子节点中最小元素并与当前根节点8交互位置,因为8>6>5,所以5与8交互位置;
然后8节点继续与其子节点进行比较,因为8>7,所以7与8交互位置。

这一出堆过程我们可以总结为以下步骤:
(1)从当前节点开始,找到其子节点元素值;
(2)比较当前节点元素值与其子节点元素值大小,如果当前节点值最小则结束调整,否则取值最小的与其交互;
(3)重复以上步骤直至处理到叶子节点。
代码实现如下:
//出堆 删除并返回堆中最小元素
public int Pop()
{if (IsEmpty()){//空堆,不可以进行删除并返回堆中最小元素操作throw new InvalidOperationException("空堆");}//取出数组第一个元素即最小元素var min = _array[0];//将数组末尾元素赋值给第一个元素_array[0] = _array[_tailIndex];//将数组末尾元素设为默认值_array[_tailIndex] = 0;//将数组末尾元素索引向前移动1位_tailIndex--;//向下调整堆,以保持堆的性质SiftDown(0);//返回最小元素return min;
}
//向下调整堆,以保持堆的性质
private void SiftDown(int index)
{while (index <= _tailIndex){//定义较小值索引变量,用于存放比较当前元素及其左右子节点元素中最小元素var minIndex = index;//计算右子节点索引var rightChildIndex = 2 * index + 2;//如果存在右子节点,则比较其与当前元素,保留值较小的索引if (rightChildIndex <= _tailIndex && _array[rightChildIndex] < _array[minIndex]){minIndex = rightChildIndex;}//计算左子节点索引var leftChildIndex = 2 * index + 1;//如果存在左子节点,则比较其与较小值元素,保留值较小的索引if (leftChildIndex <= _tailIndex && _array[leftChildIndex] < _array[minIndex]){minIndex = leftChildIndex;}//如果当前元素就是最小的,则停止调整if (minIndex == index){break;}//否则,交换当前元素和较小元素(_array[minIndex], _array[index]) = (_array[index], _array[minIndex]);//更新索引为较小值索引,继续调整index = minIndex;}
}
9、堆化 Heapify
堆化即把一个无序数组堆化成小根堆。
可以通过调用出堆是用到的调整方法来完成。大家可以思考一下为什么不是堆尾元素开始调整?为什么是从下往上调用向下调整方法调整?
//堆化,即把一个无序数组堆化成小根堆
public void Heapify(int[] array)
{if (array == null || _array.Length < array.Length){throw new InvalidOperationException("无效数组");}//将数组复制到堆中Array.Copy(array, _array, array.Length);//更新尾元素索引_tailIndex = array.Length - 1;//从最后一个非叶子节点开始向下调整堆for (int i = (array.Length / 2) - 1; i >= 0; i--){SiftDown(i);}
}
注:测试方法代码以及示例源码都已经上传至代码库,有兴趣的可以看看。https://gitee.com/hugogoos/Planner
相关文章:

数据结构 - 堆
今天我们将学习新的数据结构-堆。 01定义 堆是一种特殊的二叉树,并且满足以下两个特性: (1)堆是一棵完全二叉树; (2)堆中任意一个节点元素值都小于等于(或大于等于)左…...

html----图片按钮,商品展示
源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>图标</title><style>.box{width:…...

YOLOv11改进策略【卷积层】| ECCV-2024 小波卷积WTConv 增大感受野,降低参数量计算量,独家创新助力涨点
一、本文介绍 本文记录的是利用小波卷积WTConv模块优化YOLOv11的目标检测网络模型。WTConv的目的是在不出现过参数化的情况下有效地增加卷积的感受野,从而解决了CNN在感受野扩展中的参数膨胀问题。本文将其加入到深度可分离卷积中,有效降低模型参数量和计算量,并二次创新C3…...

redis高级篇之redis源码分析List类型quicklist底层演变 答疑159节
(1)ziplist压缩配置:list-compress-depth 0 表示一个quicklist两端不被压缩的节点个数。这里的节点是指quicklist双向链表的节点,而不是指ziplist里面的数据项个数参数list-compress-depth的取值含义如下: 0:是个特殊值,表示都不压缩。这是Redis的默认值…...

Elasticsearch 与 Lucene 的区别和联系
Elasticsearch 与 Lucene 的区别和联系 Elasticsearch 与 Lucene 的区别和联系一、知识背景Elasticsearch 简介Lucene 简介 二、Elasticsearch 和 Lucene 的区别适用场景性能优势和劣势架构设计的异同点 三、Elasticsearch和Lucene的联系四、Elasticsearch和Lucene的应用案例及…...

OpenCV视觉分析之运动分析(5)背景减除类BackgroundSubtractorMOG2的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 基于高斯混合模型的背景/前景分割算法。 该类实现了在文献[320]和[319]中描述的高斯混合模型背景减除。 cv::BackgroundSubtractorMOG2 类是 O…...

【SAP Hana】X-DOC:数据仓库ETL如何抽取SAP中的CDS视图数据
【SAP Hana】X-DOC:数据仓库ETL如何抽取SAP中的CDS视图数据 1、无参CDS对应数据库视图2、有参CDS对应数据库表函数3、封装有参CDS为无参CDS,从而对应数据库视图 1、无参CDS对应数据库视图 select * from ZFCML_REP_V where mandt 300;2、有参CDS对应数…...

WPF的UpdateSourceTrigger属性
在WPF中,UpdateSourceTrigger属性用于控制数据绑定中何时将绑定目标(通常是UI元素)的值更新回绑定源(通常是数据对象)。这个属性有以下几个值: Default:这是默认值,对于不同的绑定目…...

2024-09-25 环境变量,进程地址空间
一、认识常见的环境变量 1. echo $HOME 输出当前用户对应的家目录 当用户登录系统时,流程如下: (1)用户登录系统后,系统启动Shell程序。 (2)启动bash shell,准备接收用户指令。 &a…...

中国移动机器人将投入养老场景;华为与APUS共筑AI医疗多场景应用
AgeTech News 一周行业大事件 华为与APUS合作,共筑AI医疗多场景应用 中国移动展出人形机器人,预计投入养老等场景 作为科技与奥富能签约,共拓智能适老化改造领域 天与养老与香港科技园,共探智慧养老新模式 中山大学合作中国…...
)
青少年编程能力等级测评CPA C++ 四级试卷(1)
青少年编程能力等级测评CPA C 四级试卷(1) 一、单项选择题(共15题,每题3分,共45分) CP4_1_1.在面向对象程序设计中,与数据构成一个相互依存的整体的是( )。 A. 对数据…...

树上任意两点的距离
题目描述 给出 n 个点的一棵树,多次询问两点之间的最短距离。 注意:边是双向的。 输入描述 第一行为两个整数 n 和 m。n 表示点数,m 表示询问次数; 下来 n−1 行,每行三个整数 x,y,k,表示点 x 和点 y 之间…...

【 thinkphp8 】00008 thinkphp8数据查询,常用table,name方法,进行数据查询汇总
前言:哈喽,大家好,今天给大家分享一篇文章!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕 目录 【 t…...

Git的命令合集
关于Git的一些命令合集,会慢慢更新! 20241024程序员节开始写的,记录一下~~ git查看log、查看详细提交记录 会显示之前的提交记录 , 排序由近及远 git log log按q退出 git回退到某个commit命令: 退到/进到指定commit的sha码&…...
博客搭建之路:hexo搜索引擎收录
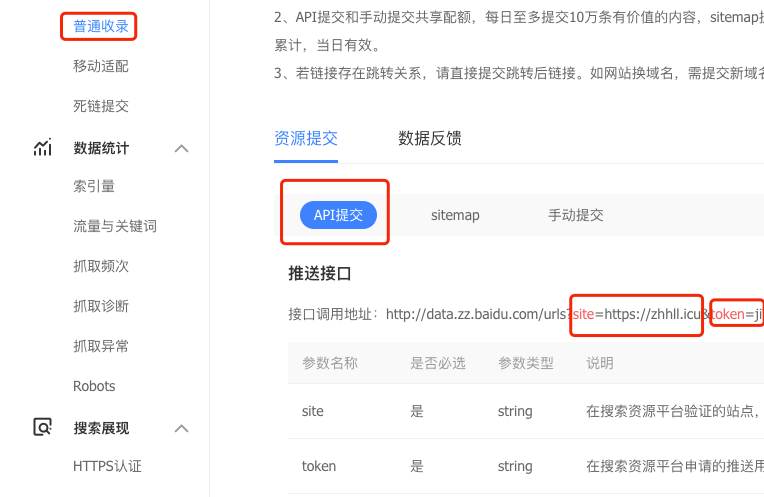
文章目录 hexo搜索引擎收录以百度为例 hexo搜索引擎收录 hexo版本5.0.2 npm版本6.14.7 next版本7.8.0 写博客的目的肯定不是就只有自己能看到,想让更多的人看到就需要可以让搜索引擎来收录对应的文章。hexo支持生成站点地图sitemap 在hexo下的_config.yml中配置站点…...

创建Windows系统还原点
系统保护...

Linux等保测评需要用到的命令
三权设置 查看账户情况 cd /home/ ll 设置审计账户 useradd shenji passwd shenji 修改密码 passwd新密码 设置管理账户 useradd guanli passwd guanli compgen -u 查看用户 切换到root账户 su root 设置审计用户权限 vim /etc/sudoers shenji ALL (root) NOPASSWD:…...

PostgreSQL的学习心得和知识总结(一百五十六)|auto_explain — log execution plans of slow queries
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库…...

数据结构模板代码合集(不完整)
P3368 【模板】树状数组 2 #include <bits/stdc.h> using namespace std; const int maxn 5e5 7;int n, m, s, t; int ans; int a[maxn]; struct node{int l, r;int num; }tr[maxn * 4];void build(int p, int l, int r){tr[p] {l, r, 0};if(l r){tr[p].num a[l];r…...

shell脚本语法详解
目录 shell语法基础 指定shell解析器 注释 运行 变量 定义变量 引用变量 清除变量值 从键盘获取值 输入单值 添加输入提示语 读取多值 编辑 定义只读变量 环境变量 设置环境变量与查看环境变量 特殊变量 三种引号的作用与区别 小括号与大括号 参数传递 位…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
