矩阵的可解性:关于Ax=b的研究
上一篇文章讲解了如何求解 A x = 0 Ax=0 Ax=0,得到 A A A的零空间。
类似的,我们今天学习的是如何求解 A x = b Ax=b Ax=b,并以此加强你对线性代数中,代数与空间的理解。
同样的,我们举与上一次一样的例子,矩阵 A A A为:
[ 1 2 2 2 2 4 6 8 3 6 8 10 ] \left[ \begin{matrix} 1 & 2 & 2 &2\\ 2 & 4 & 6&8\\ 3 & 6& 8 &10 \end{matrix} \right] 1232462682810
关于这个矩阵的详细分析与消元过程在上一篇文章讨论过,这里就不再赘述。
首先,我们将 b b b增广到矩阵 A A A中,得到如下矩阵:
∣ 1 2 2 2 b 1 2 4 6 8 b 2 3 6 8 10 b 3 ∣ \left| \begin{array}{lccc|c} {1}&{2}&{2}&{2} &{b_1}\\ {2}&{4}&{6}&{8} &{b_2}\\ {3}&{6}&{8}&{10}&{b_3} \end{array} \right| 1232462682810b1b2b3
经消元处理,能得到如下矩阵:
∣ 1 2 2 2 b 1 0 0 2 4 b 2 − 2 × b 1 0 0 0 0 b 3 − b 2 − b 1 ∣ \left| \begin{array}{lccc|c} {1}&{2}&{2}&{2} &{b_1}\\ {0}&{0}&{2}&{4} &{b_2-2\times b_1}\\ {0}&{0}&{0}&{0}&{b_3-b_2-b_1} \end{array} \right| 100200220240b1b2−2×b1b3−b2−b1
在继续进行下一步操作前,让我们想一想这个问题: A x = b Ax=b Ax=b在何时有解?
观察消元过后的第三行,不难发现, b b b的元素应该满足 b 3 − b 2 − b 1 = 0 b_3-b_2-b_1=0 b3−b2−b1=0,这样才能使矩阵第三行成立。对这个结论进行拓展,不难想到,当 b b b在矩阵 A A A的列空间内时,方程有解。明白这一点也会对我们接下来的操作有指导意义。
如同我们求零空间的方法,我们利用消元过后的自由列能快速得到一个关于 A x = b Ax=b Ax=b的特殊解。
具体到这道题上,我们可以看到 A 1 , 1 与 A 2 , 3 A_{1,1}与A_{2,3} A1,1与A2,3为主元。因为自由列的变量可以取任意值,为求计算方便,我们一般取其为0,即 x 2 = 0 , x 4 = 0 x_2=0,x_4=0 x2=0,x4=0。
那么此时的方程就变为了这样:
x 1 + 2 x 3 = b 1 2 × x 2 = b 2 − 2 b 1 x_1+2x_3=b_1 \\ 2 \times x_2 = b_2-2b_1 x1+2x3=b12×x2=b2−2b1
因为 b 1 , b 2 b_1,b_2 b1,b2为参数,所以现在我们就求得了特解 x p a r t i c u l a r , 即 x p x_{particular},即x_p xparticular,即xp
又一次同样的,我们采用求零空间时的方法,利用特解来求得所有的解,而这里也会用上零空间 N N N,设其中任意的元素为 n n n吧。
那么,我们有:
A x p = b A n = 0 Ax_p=b \\ An = 0 Axp=bAn=0
不难发现, A ( x p + n ) = b A(x_p+n)=b A(xp+n)=b,即特解加上零空间的和后得到的向量同样是方程的解。不妨猜想,特解加上零空间即使所有的解。前面证明了充分性,下面证明必要性:
设 x x x为一个任意的方程的解,有
A x = b A x p = b → A ( x − x P ) = 0 Ax=b \\ Ax_p=b \\ \rightarrow A(x-x_P)=0 Ax=bAxp=b→A(x−xP)=0
换言之 n + x p = x n+x_p=x n+xp=x
证得必要性成立。
所以,我们得到了 A x = b Ax=b Ax=b的解,即为其特解加上 A A A的零空间。
此时,再来想象一下,零空间是经过原点的向量空间,那么 A x = b Ax=b Ax=b的解就应是将零空间向特解的方向平移过去所得。要注意的是,其解并不包含原点,所以不是向量空间。
相关文章:

矩阵的可解性:关于Ax=b的研究
上一篇文章讲解了如何求解 A x 0 Ax0 Ax0,得到 A A A的零空间。 类似的,我们今天学习的是如何求解 A x b Axb Axb,并以此加强你对线性代数中,代数与空间的理解。 同样的,我们举与上一次一样的例子,矩阵 …...
10.22.2024刷华为OD C题型(三)--for循环例子
脚踝动了手术,现在宾馆恢复,伤筋动骨一百天还真不是说笑的,继续努力吧。 文章目录 靠谱的车灰度图恢复灰度图恢复 -- for循环使用例子 靠谱的车 https://www.nowcoder.com/discuss/564514429228834816 这个题目思路不难,就是要自…...
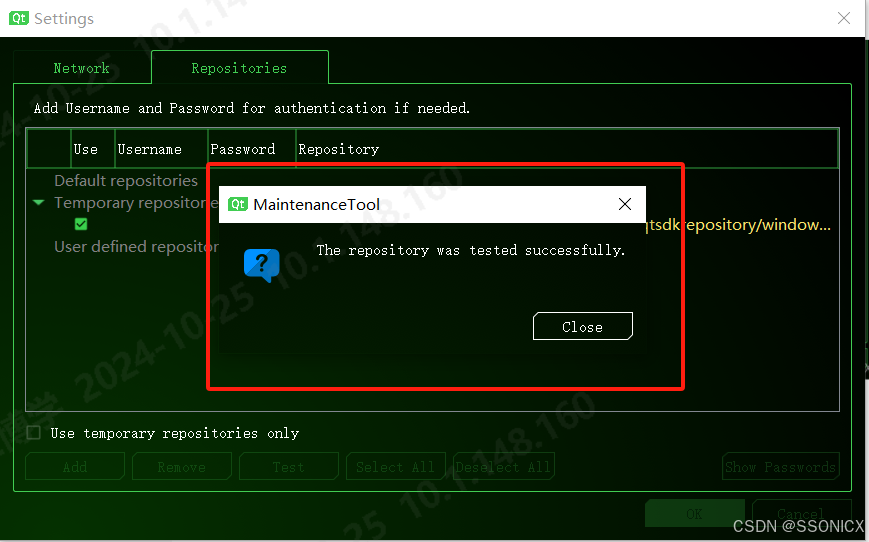
QT:MaintenanceTool 模块安装工具
QT的MaintenanceTool 工具对已安装的 Qt 进行卸载、修复等其他操作时提示At least one valid and enabled repository required for this action to succeed 解决方式:在设置中添加一个临时的仓库 https://mirrors.tuna.tsinghua.edu.cn/qt/online/qtsdkrepositor…...

同标签实现监听LocalStorage
使用 React 生命周期函数 useEffect来监听和处理 LocalStorage 的变化 import React, { useEffect } from react;const LocalStorageListener () > {useEffect(() > {// 注册监听器const handleStorageChange (event) > {if (event.key myKey) {console.log(注册…...

JAVA高性能缓存项目
版本一 代码实现 import java.util.HashMap; import java.util.concurrent.TimeUnit;public class CacheExample01 {private final static HashMap<String, Integer> cache new HashMap<>();public static Integer check(String userId) throws InterruptedExce…...

智慧农业大数据平台:智汇田园,数驭未来
智慧农业大数据平台 计讯物联智慧农业大数据平台是一个集管理数字化、作业自动化、生产智能化、产品绿色化、环境信息化、服务现代化于一体的多功能监管系统。它通过与硬件产品的搭配使用,实现对农业生产全过程的实时监测、精准控制和科学管理。该平台集成了多个数…...
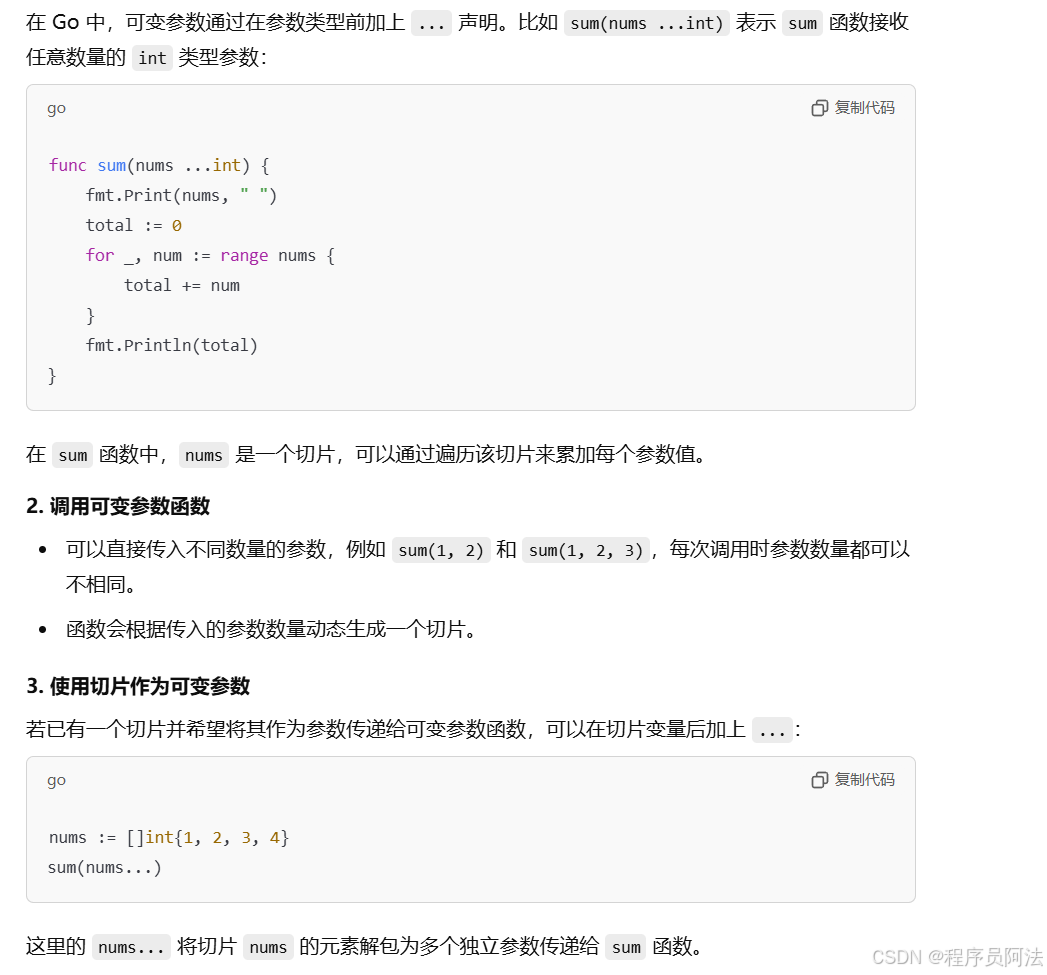
Go语言基础教程:可变参数函数
Go 语言允许函数接收可变数量的参数,这种特性对于处理数量不确定的参数特别有用。在本教程中,我们将通过示例代码讲解如何定义和使用 Go 的可变参数函数。 package mainimport "fmt"// 定义一个可变参数函数 sum,接收任意数量的整…...

高并发场景下解决并发数据不一致
简单的场景: 全量数据更新的情况下, 不在乎同一秒的请求都必须要成功, 只留下最新的更新请求数据 方案常用的是 1、数据库增加时间戳标识实现的乐观锁, 请求参数从源头带上微秒或者毫秒时间戳数据库存储, 然后在更新SQL语句上比较 (数据库的时间 < 参数传递的时间) 例如: A…...
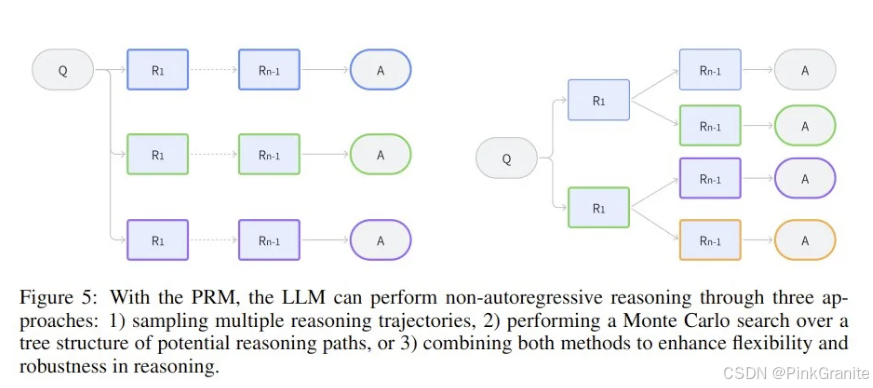
OpenAI GPT-o1实现方案记录与梳理
本篇文章用于记录从各处收集到的o1复现方案的推测以及介绍 目录 Journey Learning - 上海交通大学NYUMBZUAIGAIRCore IdeaKey QuestionsKey TechnologiesTrainingInference A Tutorial on LLM Reasoning: Relevant methods behind ChatGPT o1 - UCL汪军教授Core Idea先导自回归…...
Excel:vba实现生成随机数
Sub 生成随机数字()Dim randomNumber As IntegerDim minValue As IntegerDim maxValue As Integer 设置随机数的范围(假入班级里面有43个学生,学号是从1→43)minValue 1maxValue 43 生成随机数(在1到43之间生成随机数)randomNumber Application.WorksheetFunctio…...

Python | Leetcode Python题解之第506题相对名次
题目: 题解: class Solution:desc ("Gold Medal", "Silver Medal", "Bronze Medal")def findRelativeRanks(self, score: List[int]) -> List[str]:ans [""] * len(score)arr sorted(enumerate(score), …...
)
安全见闻(6)
声明:学习视频来自b站up主 泷羽sec,如涉及侵权马上删除文章 感谢泷羽sec 团队的教学 视频地址:安全见闻(6)_哔哩哔哩_bilibili 学无止境,开拓自己的眼界才能走的更远 本文主要讲解通讯协议涉及的安全问题。…...

Promise、async、await 、异步生成器的错误处理方案
1、Promise.all 的错误处理 Promise.all 方法接受一个 Promise 数组,并返回所有解析 Promise 的结果数组: const promise1 Promise.resolve("one"); const promise2 Promise.resolve("two");Promise.all([promise1, promise2]).…...

腾讯云:数智教育专场-学习笔记
15点13分2024年10月21日(短短5天的时间,自己的成长速度更加惊人)-开始进行“降本增效”学习模式,根据小米手环对于自己的行为模式分析(不断地寻找数据之间的关联性),每天高效记忆时间࿰…...

Ovis: 多模态大语言模型的结构化嵌入对齐
论文题目:Ovis: Structural Embedding Alignment for Multimodal Large Language Model 论文地址:https://arxiv.org/pdf/2405.20797 github地址:https://github.com/AIDC-AI/Ovis/?tabreadme-ov-file 今天,我将分享一项重要的研…...

python的Django的render_to_string函数和render函数模板的使用
一、render_to_string render_to_string 是 Django 框架中的一个便捷函数,用于将模板渲染为字符串。 render_to_string(template_name.html, context, requestNone, usingNone) template_name.html:要渲染的模板文件的名称。context:传递给…...
基于Python大数据的王者荣耀战队数据分析及可视化系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码、微信小程序源码 精品专栏:…...

【Linux学习】(3)Linux的基本指令操作
前言 配置Xshell登录远程服务器Linux的基本指令——man、cp、mv、alias&which、cat&more&less、head&tail、date、cal、find、grep、zip&tar、bc、unameLinux常用热键 一、配置Xshell登录远程服务器 以前我们登录使用指令: ssh 用户名你的公网…...

Mac 使用脚本批量导入 Apple 歌曲
最近呢,买了一个 iPad,虽然家里笔记本台式都有,显示器都是 2个,比较方便看代码(边打游戏边追剧)。 但是在床上拿笔记本始终还是不方便,手机在家看还是小了点,自从有 iPad 之后&…...

全桥PFC电路及MATLAB仿真
一、PFC电路原理概述 PFC全称“Power Factor Correction”(功率因数校正),PFC电路即能对功率因数进行校正,或者说是能提高功率因数的电路。是开关电源中很常见的电路。功率因数是用来描述电力系统中有功功率(实际使用…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
