蓝桥杯备考——算法
一、排序
冒泡排序、选择排序、插入排序、 快速排序、归并排序、桶排序
二、枚举
三、二分查找与二分答案
四、搜索(DFS)
DFS(DFS基础、回溯、剪枝、记忆化)
1.DFS算法(深度优先搜索算法)
深度优先搜索( DFS )是一种用于遍历或搜索图或树的算法,它从起始节点开始,沿着一条路径一直深入直到无法继续为止,然后回溯到上一个节点继续探索。 DFS 使用栈来记录遍历的路径,它优先访问最近添加到栈的节点。
DFS 的主要优点是简单且易于实现,它不需要额外的数据结构来记录节点的访问情况,仅使用栈来存储遍历路径。然而, DFS 可能会陷入无限循环中,因为它不考虑节点是否已经访问过。
对于一个连通图,深度优先搜索遍历的过程如下:
(1)从图中某个顶点v出发,访问v;
(2)找到刚访问过的顶点的第一个未被访问的邻接点,访问该顶点。 以该顶点为新顶点,重 复此步骤, 直至刚访问过的顶点没有未被访问的邻接点为止。
(3)返回前一个访问过的且仍有未被访问的邻接点的顶点,找出该顶点的下一个未被访问的邻接点, 访问该顶点。
(4)重复步骤 (2) 和(3), 直至图中所有顶点都被访问过,搜索结束。

顶点访问序列:v1 -> v2 -> v4 -> v8 -> v5 -> v3 -> v6 -> v7
DFS 使用栈来记录遍历的路径,它优先访问最近添加到栈的节点。
显然, 深度优先搜索遍历连通图是一个递归的过程。 为了在遍历过程中便千区分顶点是否已
被访问,需附设访问标志数组 visited[n] , 其初值为 "false", 一旦某个顶点被访问,则其相应的分
量置为 "true"。
python语言:
# 图的DFS遍历
def dfs(graph, start, visited):# 访问当前节点print(start, end=' ')# 标记当前节点为已访问visited[start] = True# 遍历当前节点的邻居节点for neighbor in graph[start]:# 如果邻居节点未被访问,则继续深度优先搜索if not visited[neighbor]:dfs(graph, neighbor, visited)# 图的邻接表表示
graph = {'1': ['2', '3'],'2': ['2', '4', '5'],'3': ['1', '6', '7'],'4': ['2','8'],'5': ['2','8'],'6': ['3','7'],'7': ['3','6'],'8': ['4','5']
}# 标记节点是否已访问的列表
visited = {node: False for node in graph}# 从节点A开始进行DFS遍历
print("DFS遍历结果:")
dfs(graph, '1', visited)C++ / C语言:
算法1.深度优先搜索遍历连通图
// 1. 深度优先搜索遍历连通图
bool visited[MVNum]; // 访问标志数组,其初值设为“false”
void DFS(Graph G, int v)
{ // 从第v个顶点出发 递归地深度优先遍历图Gcout << v; visited[v] = true;for (w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v,w))// 依次检查v的所有邻接点w,FirstAdjVex(G,v)表示v的第一个邻接点// NextAdjVex(G,v,w)表示v相对于w的下一个邻接点,w>=0表示存在邻接点if (!visited[w]) DFS(G,w); // 对v的尚未访问的邻接点w递归调用DFS
}算法2.深度优先搜索遍历 非连通图
若是非连通图, 上述遍历过程执行之后, 图中一定还有顶点未被访间,需要从图中另选
一个未被访问的顶点作为起始点 , 重复上述深度优先搜索过程, 直到图中所有顶点均被访问
过为止。这样, 要实现对非连通图的遍历,需要循环调用算法 1, 具体实现如算法 2所示。
void DFSTraverse(Graph G)
{ //对非连通图G做深度优先遍历for(v=O;v<G.vexnum;++v) visited[v]=false; // 访问标志数组初始化for(v=O;v<G.vexnum;++v) // 循环调用算法1if(!visited[v]) DFS(G,v); // 对尚未访问的顶点调用DFS
}算法 3 采用 邻接矩阵 表示图的深度优先搜索遍历
void DFS_AM(AMGraph G,int v)
{ // 图G为 邻接矩阵类型,从第v个顶点出发深度优先搜索遍历图Gcout<<v; visited[v]=true; // 访问第v个顶点,并置访问标志数组相应分址值为truefor(w=O; w<G.vexnum; w++) // 依次检查邻接矩阵 v所在的行if((G.arcs[v][w] !=O) && (!visited[w])) DFS(G,w); //G.arcs[v][w] ! =0表示w是v的邻接点, 如果w未访问, 则递归调用DFS
}算法 4 采用邻接表表示图的深度优先搜索遍历
void DFS_AL (ALGraph G,int v)
{ //图G为 邻接表 类型, 从第v个顶点出发深度优先搜索遍历图Gcout<<v; visited[v]=true; // 访问第v个顶点,并置访问标志数组相应分量值为truep=G.vertices[v] .firstarc; //p指向v的边链表的第一个边结点while(p!=NULL) // 边结点非空{w=p->adjvex; // 表示w是v的邻接点if(!visited[w]) DFS(G,w); // 如果w未访问, 则递归调用DFSp=p->nextarc; //p指向下一个边结点}
}例题:1.最大连通
问题描述:(填空题)
小兰有一个30行60列的数字矩阵,矩阵中的每个数都是0或1。
110010000011111110101001001001101010111011011011101001111110010000000001010001101100000010010110001111100010101100011110 001011101000100011111111111010000010010101010111001000010100 101100001101011101101011011001000110111111010000000110110000 010101100100010000111000100111100110001110111101010011001011 010011011010011110111101111001001001010111110001101000100011 101001011000110100001101011000000110110110100100110111101011 101111000000101000111001100010110000100110001001000101011001 001110111010001011110000001111100001010101001110011010101110 001010101000110001011111001010111111100110000011011111101010 011111100011001110100101001011110011000101011000100111001011 011010001101011110011011111010111110010100101000110111010110 001110000111100100101110001011101010001100010111110111011011 111100001000001100010110101100111001001111100100110000001101 001110010000000111011110000011000010101000111000000110101101 100100011101011111001101001010011111110010111101000010000111 110010100110101100001101111101010011000110101100000110001010 110101101100001110000100010001001010100010110100100001000011 100100000100001101010101001101000101101000000101111110001010 101101011010101000111110110000110100000010011111111100110010 101111000100000100011000010001011111001010010001010110001010 001010001110101010000100010011101001010101101101010111100101 001111110000101100010111111100000100101010000001011101100001 101011110010000010010110000100001010011111100011011000110010 011110010100011101100101111101000001011100001011010001110011 000101000101000010010010110111000010101111001101100110011100 100011100110011111000110011001111100001110110111001001000111 111011000110001000110111011001011110010010010110101000011111 011110011110110110011011001011010000100100101010110000010011 010011110011100101010101111010001001001111101111101110011101如果从一个标为1的位置可以通过上下左右走到另一个标为1的位置,则称两个位置连通。与某一个标为1的位置连通的所有位置(包括自己)组成一个连通分块。
请问矩阵中最大的连通分块有多大?
答案:
import os
import sysdef dfs(x, y, num): # x,y是当前的位置,num是最大连通的数量vis[x][y] = 1 # 表明这个位置已经被搜素过了for dx,dy in [(1, 0), (-1, 0), (0,1), (0, -1)]: # 标准的上下左右搜索current_x = x + dxcurrent_y = y + dyif 0 <= current_x < 30 and 0 <= current_y <60: # 边界限制try:if vis[current_x][current_y] != 1 and data[current_x][current_y] == '1': # 上下左右有位置没有被探索同时还是字符串的'1'num = dfs(current_x,current_y,num)except: # 这里是方便找到如果输入错误是在哪,用来检查循环条件是否写错print(current_x)print(current_y)return num + 1 # 本身的1加上所有与它相连的numdata =[
"110010000011111110101001001001101010111011011011101001111110","010000000001010001101100000010010110001111100010101100011110","001011101000100011111111111010000010010101010111001000010100","101100001101011101101011011001000110111111010000000110110000","010101100100010000111000100111100110001110111101010011001011","010011011010011110111101111001001001010111110001101000100011","101001011000110100001101011000000110110110100100110111101011","101111000000101000111001100010110000100110001001000101011001","001110111010001011110000001111100001010101001110011010101110","001010101000110001011111001010111111100110000011011111101010","011111100011001110100101001011110011000101011000100111001011","011010001101011110011011111010111110010100101000110111010110","001110000111100100101110001011101010001100010111110111011011","111100001000001100010110101100111001001111100100110000001101","001110010000000111011110000011000010101000111000000110101101","100100011101011111001101001010011111110010111101000010000111","110010100110101100001101111101010011000110101100000110001010","110101101100001110000100010001001010100010110100100001000011","100100000100001101010101001101000101101000000101111110001010","101101011010101000111110110000110100000010011111111100110010","101111000100000100011000010001011111001010010001010110001010","001010001110101010000100010011101001010101101101010111100101","001111110000101100010111111100000100101010000001011101100001","101011110010000010010110000100001010011111100011011000110010","011110010100011101100101111101000001011100001011010001110011","000101000101000010010010110111000010101111001101100110011100","100011100110011111000110011001111100001110110111001001000111","111011000110001000110111011001011110010010010110101000011111","011110011110110110011011001011010000100100101010110000010011","010011110011100101010101111010001001001111101111101110011101"]
res = 0
vis = [[0 for i in range(60)] for j in range(30)] # 标记数组
for i in range(30): # i和j是位置for j in range(60):if data[i][j] == '1' and vis[i][j] == 0:num = 0num = dfs(i,j,num)res = max(num, res)
print(res)例题2.
2. 广度优先搜索( BFS )算法
是一种用于遍历或搜索图或树的算法,它从起始节点开始,逐层地向外扩展,先访问当前节点的所有邻居节点,然后再访问邻居节点的邻居节点,直到遍历完所有节点。
BFS 使用队列来记录遍历的路径,它优先访问最早添加到队列的节点。 BFS 的主要优点是能够找到起始节点到目标节点的最短路径,因为它是逐层遍历的。

python语言
from collections import deque# 图的BFS遍历
def bfs(graph, start):# 使用队列来记录遍历路径queue = deque([start])# 标记节点是否已访问的集合visited = set([start])while queue: # 当栈不为空node = queue.popleft() # 左端出栈print(node, end=' ')for neighbor in graph[node]:if neighbor not in visited:queue.append(neighbor) # 右端进栈visited.add(neighbor)# 图的邻接表表示
graph = {'1': ['2', '3'],'2': ['2', '4', '5'],'3': ['1', '6', '7'],'4': ['2','8'],'5': ['2','8'],'6': ['3','7'],'7': ['3','6'],'8': ['4','5']
}# 从节点A开始进行BFS遍历
print("BFS遍历结果:")
bfs(graph, '1') # 1 2 3 4 5 6 7 8python: collections模块——双向队列(deque)
类似于list的容器,可以快速的在队列头部和尾部添加、删除元素
3. DFS 与 BFS 的对比
DFS 和 BFS 是两种不同的图遍历算法,在不同的应用场景下具有不同的优势:
- DFS 适用于找到起始节点到目标节点的路径,但不一定是最短路径。它通过递归的方式深入探索图的分支,因此对于深度较小的图或树, DFS 通常表现较好。
- BFS 适用于找到起始节点到目标节点的最短路径。它通过逐层遍历图的节点,从而保证找到的路径是最短的。在需要寻找最短路径的情况下, BFS 是更好的选择
相关文章:

蓝桥杯备考——算法
一、排序 冒泡排序、选择排序、插入排序、 快速排序、归并排序、桶排序 二、枚举 三、二分查找与二分答案 四、搜索(DFS) DFS(DFS基础、回溯、剪枝、记忆化) 1.DFS算法(深度优先搜索算法) 深度优先搜…...

MutationObserver与IntersectionObserver的区别
今天主要是分享一下MutationObserver和IntersectionObserver的区别,希望对大家有帮助! MutationObserver 和 IntersectionObserver 的区别 MutationObserver 作用:用于监听 DOM 树的变动,包括:元素的属性、子元素列表或节点文本的…...
生产与配置
1.鲁滨孙克苏鲁经济 鲁滨孙克苏鲁经济是一种非常简单的自给自足的经济,劳动时间与休息时间总和为总的时间。 即 摘椰子的数量为劳动时间的函数 由于鲁滨孙喜欢椰子,厌恶劳动时间,因此无差异曲线表现为厌恶品的形态。 根据无差异曲线和生…...

Android Kotlin Flow 冷流 热流
在 Android 开发中,Flow 是 Kotlin 协程库的一部分,用于处理异步数据流的一个组件。本质上,Flow 是一个能够异步生产多个值的数据流,与 suspend 函数返回单个值的模式相对应。Flow 更类似于 RxJava 中的 Observable,但…...

订单日记助力“实峰科技”提升业务效率
感谢北京实峰科技有限公司选择使用订单日记! 北京实峰科技有限公司,成立于2022年,位于北京市石景区,是一家以从事生产、销售微特电机、输配电及控制设备等业务为主的企业。 在业务不断壮大的过程中,想使用一种既能提…...

如何安装和配置JDK17
教程目录 零、引言1、新特性概览2、性能优化3、安全性增强4、其他改进5、总结 一、下载安装二、环境配置三、测试验证 零、引言 JDK 17(Java Development Kit 17)是Java平台的一个重要版本,它带来了许多新特性和改进,进一步提升了…...

智能化温室大棚控制系统设计(论文+源码)
1 系统的功能及方案设计 本次智能化温室大棚控制系统的设计其系统整体结构如图2.1所示,整个系统在器件上包括了主控制器STC89C52,温湿度传感器DHT11,LCD1602液晶,继电器,CO2传感器,光敏电阻,按…...

面试题之---解释一下原型和原型链
实例化对象 和普调函数一样,只不过调用的时候要和new连用(实例化),不然就是一个普通函数调用 function Person () {} const o1 new Person() //能得到一个空对象 const o2 Person() //什么也得不到,这就是普通的…...

【Leecode】Leecode刷题之路第46天之全排列
题目出处 46-全排列-题目出处 题目描述 个人解法 思路: todo代码示例:(Java) todo复杂度分析 todo官方解法 46-全排列-官方解法 预备知识 回溯法:一种通过探索所有可能的候选解来找出所有的解的算法。如果候选解…...

自动驾驶革命:从特斯拉到百度,谁将主宰未来交通?
内容概要 自动驾驶技术正在经历一个前所未有的革命性变化,各大企业纷纷抢占这一充满潜力的新市场。以特斯拉和百度为代表的行业巨头,正利用各自的优势在这一技术的赛道上展开激烈竞争。特斯拉凭借其在电动汽车和自动驾驶领域的前瞻性设计与不断革新的技…...
方法)
Python __str__()方法
在Python中,str() 方法是一个特殊的方法(也称为魔术方法或双下方法),它定义了当对象需要被转换为字符串表示时应该如何做。 当你尝试打印对象(使用 print() 函数)或将对象插入到需要字符串表示的上下文中&…...

虚拟机的安装
添加映像文件 自动或者手动分配磁盘 添加密码 创建用户 创建快照...

HCIP快速生成树 RSTP
STP(Spanning Tree Protocol,生成树协议)和RSTP(Rapid Spanning Tree Protocol,快速生成树协议)都是用于在局域网中消除环路的网络协议。 STP(生成树协议) 基本概念: ST…...

Python基础学习-05元组 tuple
目录 1、元组的定义 2、元组的切片和索引 3、元组的函数 4、二维元组 5、本节总结 1、元组的定义 • 基本上可以理解为一个不可改变的列表 • 元组没有列表那么常用,但是它的关键是不可改变性 • 使用() 定义一个元组 1) T (1, 2, 3, 4, …...
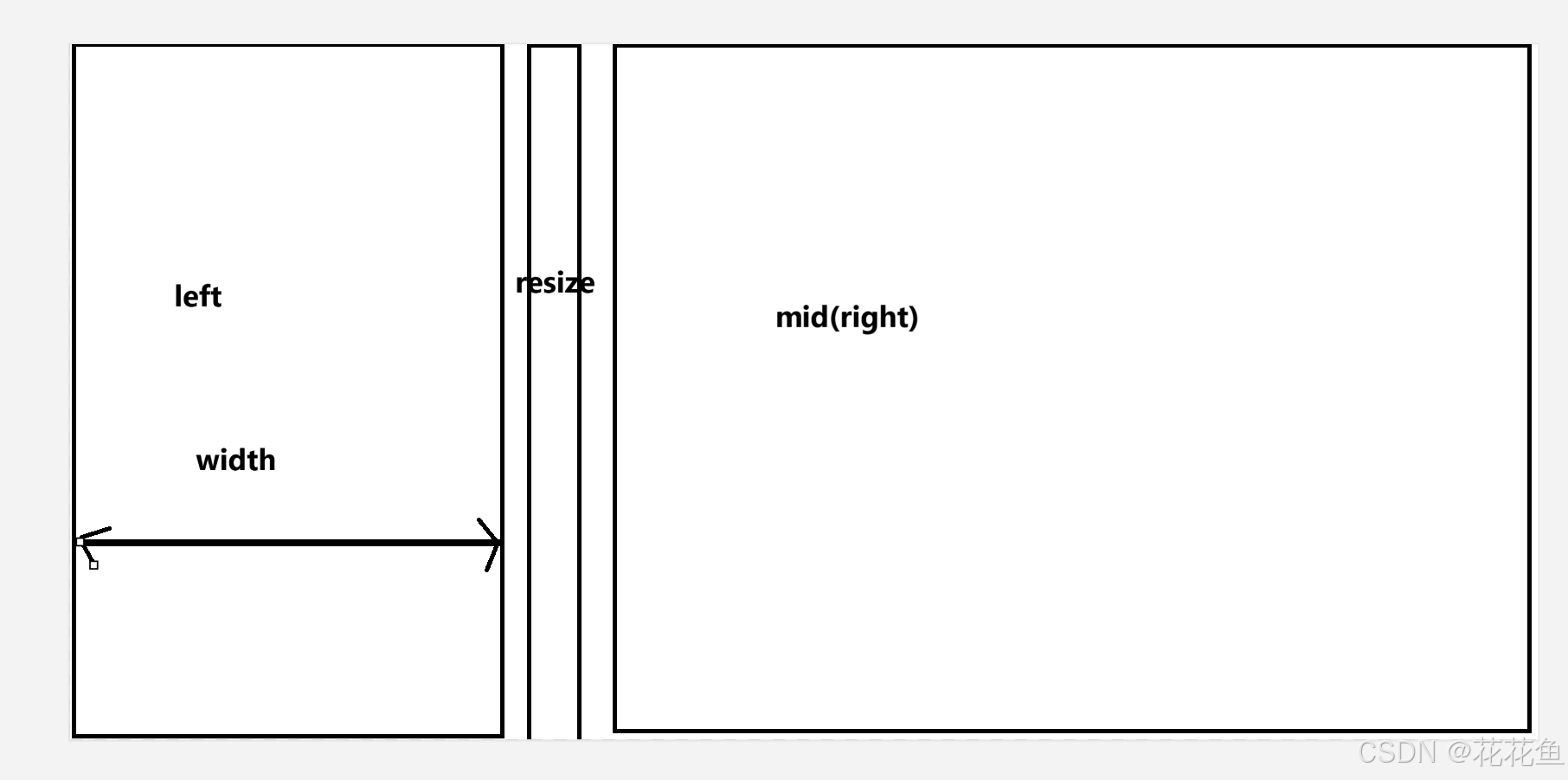
vue3 基于element-plus进行的一个可拖动改变导航与内容区域大小的简单方法
1、先上个截图: 说明:拖动上面的分隔栏就可以实现,改变左右区域的大小。 2、上面的例子来自官网的: Container 布局容器 | Element Plus 3、拖动的效果来自: https://juejin.cn/post/7029640316999172104#heading-1…...

c++基础28函数的类型
函数的类型 基本用法例子usingfucntion 基本用法 在C中,函数类型是指函数的签名,包括返回类型、参数类型以及参数的数量。函数类型可以用来声明函数指针、函数引用或者作为模板参数。 函数也可当成一种数据类型 函数指针: 函数指针可以指向…...

Elasticsearch(四):query_string查询介绍
query_string查询介绍 1 概述2 基本概念3 数据准备4 query_string查询示例4.1 基本查询4.2 复杂查询解析4.3 高级过滤解析4.4 模糊查询解析4.5 高亮查询解析4.6 分页查询解析 5 总结 大家好,我是欧阳方超,可以我的公众号“欧阳方超”,后续内容…...

超好用shell脚本NuShell mac安装
利用管道控制任意系统 Nu 可以在 Linux、macOS 和 Windows 上运行。一次学习,处处可用。 一切皆数据 Nu 管道使用结构化数据,你可以用同样的方式安全地选择,过滤和排序。停止解析字符串,开始解决问题。 强大的插件系统 具备强…...

Vue禁止打开控制台/前端禁止打开控制台方法/禁用F12/禁用右键
代码片段展示了如何在前端页面中禁用右键菜单、禁止文本选择、阻止特定键盘操作(如F12键打开开发者工具),以及通过检测窗口尺寸变化来尝试阻止用户调试页面。 // 鼠标禁止右键禁止打开控制台及键盘禁用forbidden(){// 1.禁用右键菜单document…...

volatile关键字
1. 可见性 当一个变量被声明为 volatile 时,任何线程对该变量的写入操作都会立即对其他线程可见。这意味着: 当一个线程修改了 volatile 变量的值,其他线程在读取这个变量时会看到最新的值,而不是可能被缓存的旧值。 这解决了多线…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
