【复平面】-复数相乘的几何性质
文章目录
- 从数学上证明
- 1. 计算乘积 z 1 ⋅ z 2 z_1 \cdot z_2 z1⋅z2
- 2. 应用三角恒等式
- 3. 得出结果
- 从几何角度证明
首先说结论:
在复平面中,两个复数(即向量)相乘时,满足模长相乘,角度相加的性质。
从数学上证明
假设两个复数 ( z 1 z_1 z1 ) 和 ( z 2 z_2 z2 ) 表示为:
z 1 = r 1 ( cos θ 1 + i sin θ 1 ) z_1 = r_1 (\cos \theta_1 + i \sin \theta_1) z1=r1(cosθ1+isinθ1)
z 2 = r 2 ( cos θ 2 + i sin θ 2 ) z_2 = r_2 (\cos \theta_2 + i \sin \theta_2) z2=r2(cosθ2+isinθ2)
其中:
- ( r 1 = ∣ z 1 ∣ r_1 = |z_1| r1=∣z1∣ ) 和 ( r 2 = ∣ z 2 ∣ r_2 = |z_2| r2=∣z2∣ ) 分别是 ( z 1 z_1 z1 ) 和 ( z 2 z_2 z2 ) 的模长,
- ( θ 1 \theta_1 θ1 ) 和 ( θ 2 \theta_2 θ2 ) 分别是 ( z 1 z_1 z1 ) 和 ( z 2 z_2 z2 ) 的辐角(即相对于实轴的角度)。
1. 计算乘积 z 1 ⋅ z 2 z_1 \cdot z_2 z1⋅z2
我们将 ( z 1 z_1 z1 ) 和 ( z 2 z_2 z2 ) 相乘,得到:
z 1 ⋅ z 2 = r 1 ( cos θ 1 + i sin θ 1 ) ⋅ r 2 ( cos θ 2 + i sin θ 2 ) z_1 \cdot z_2 = r_1 (\cos \theta_1 + i \sin \theta_1) \cdot r_2 (\cos \theta_2 + i \sin \theta_2) z1⋅z2=r1(cosθ1+isinθ1)⋅r2(cosθ2+isinθ2)
使用分配律展开:
z 1 ⋅ z 2 = r 1 r 2 [ ( cos θ 1 cos θ 2 − sin θ 1 sin θ 2 ) + i ( cos θ 1 sin θ 2 + sin θ 1 cos θ 2 ) ] z_1 \cdot z_2 = r_1 r_2 \left[ (\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2) + i (\cos \theta_1 \sin \theta_2 + \sin \theta_1 \cos \theta_2) \right] z1⋅z2=r1r2[(cosθ1cosθ2−sinθ1sinθ2)+i(cosθ1sinθ2+sinθ1cosθ2)]
2. 应用三角恒等式
根据加法公式的三角恒等式,有:
cos ( θ 1 + θ 2 ) = cos θ 1 cos θ 2 − sin θ 1 sin θ 2 \cos(\theta_1 + \theta_2) = \cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 cos(θ1+θ2)=cosθ1cosθ2−sinθ1sinθ2
sin ( θ 1 + θ 2 ) = cos θ 1 sin θ 2 + sin θ 1 cos θ 2 \sin(\theta_1 + \theta_2) = \cos \theta_1 \sin \theta_2 + \sin \theta_1 \cos \theta_2 sin(θ1+θ2)=cosθ1sinθ2+sinθ1cosθ2
将这些恒等式代入到上面的表达式中,我们得到:
z 1 ⋅ z 2 = r 1 r 2 ( cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) ) z_1 \cdot z_2 = r_1 r_2 \left( \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2) \right) z1⋅z2=r1r2(cos(θ1+θ2)+isin(θ1+θ2))
3. 得出结果
根据复数的极坐标形式,这个结果可以写成:
z 1 ⋅ z 2 = r 1 r 2 ⋅ e i ( θ 1 + θ 2 ) z_1 \cdot z_2 = r_1 r_2 \cdot e^{i (\theta_1 + \theta_2)} z1⋅z2=r1r2⋅ei(θ1+θ2)
因此,我们得出结论:两个复数相乘时,其模长是各自模长的乘积,辐角是各自辐角的和,即满足“模长相乘,角度相加”的性质。
从几何角度证明
本质上就是坐标轴的变换
1.给出待乘的复数 u i u_i ui
{ u = a + b i u i = − b + a i \left\{\begin{array}{l} u=a+b i \\ u i=-b+a i \end{array}\right. {u=a+biui=−b+ai
( a , b ) ⋅ ( − b , a ) = 0 (a,b)\cdot(-b,a)=0 (a,b)⋅(−b,a)=0由于内积为0,故u与ui正交
2.给出任意复数 l l l
所以 ∀ l = x + y i \forall l=x+y_{i} ∀l=x+yi与u相乘可以在新的坐标轴u、ui下表示,其与坐标轴角度与在原先坐标轴下相同。
所以两个复数(即向量)相乘时,满足角度相加的性质。
{ ∀ l = x + y i l ⋅ u = ( x + y i ) ⋅ u = x u + y u i \left\{\begin{array}{l} \forall l=x+y_{i} \\ l \cdot u=\left(x+y_{i}\right) \cdot u=x u+y u i \end{array}\right. {∀l=x+yil⋅u=(x+yi)⋅u=xu+yui
3.复数 l l l 在不同坐标轴下的表示图
 |  |
相关文章:

【复平面】-复数相乘的几何性质
文章目录 从数学上证明1. 计算乘积 z 1 ⋅ z 2 z_1 \cdot z_2 z1⋅z22. 应用三角恒等式3. 得出结果 从几何角度证明1.给出待乘的复数 u i u_i ui2.给出任意复数 l l l3.复数 l l l 在不同坐标轴下的表示图 首先说结论: 在复平面中,两个复数&a…...

为什么ta【给脸不要脸】:利他是一种选择,善良者的自我救赎与智慧策略
你满腔热忱,他却视而不见; 你伸出援手,他却恩将仇报; 你谦让包容,他却得寸进尺; 你善意提拔,他却并不领情,反而“给脸不要脸”。 所有人都曾被这种“好心当成驴肝肺”遭遇内耗&a…...

mysql 配置文件 my.cnf 增加 lower_case_table_names = 1 服务启动不了的原因
原因:在MySQL8.0之后的版本,只允许在数据库初始化时指定,之后不允许修改了 mysql 配置文件 my.cnf 增加 lower_case_table_names 1 服务启动不了 报错信息:Job for mysqld.service failed because the control process exited …...
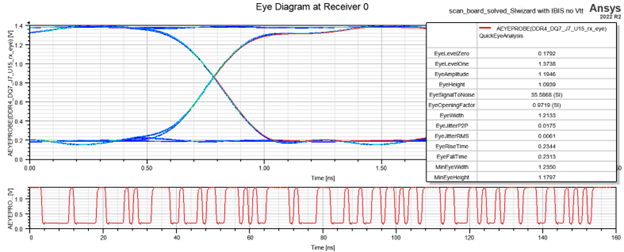
SIwave:释放 SIwizard 求解器的强大功能
SIwave 是一种电源完整性和信号完整性工具。SIwizard 是 SIwave 中 SI 分析的主要工具,也是本博客的主题。 SIwizard 用于研究 RF、clock 和 control traces 的信号完整性。该工具允许用户进行瞬态分析、眼图分析和 BER 计算。用户可以将 IBIS 和 IBIS-AMI 模型添加…...
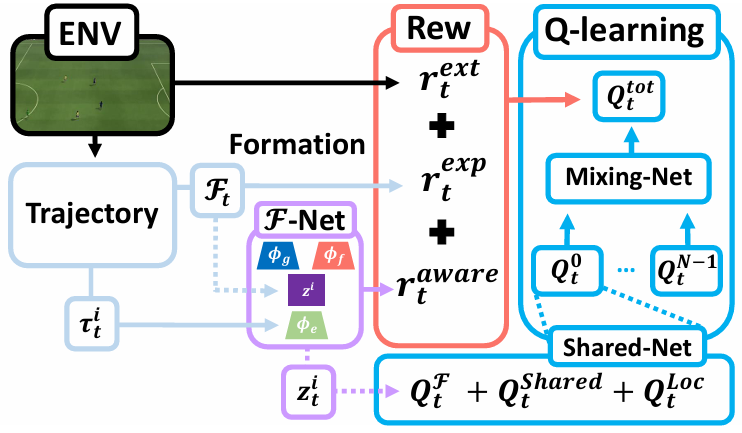
强化学习不愧“顶会收割机”!2大创新思路带你上大分,毕业不用愁!
强化学习之父Richard Sutton悄悄搞了个大的,提出了一个简单思路:奖励聚中。这思路简单效果却不简单,等于是给几乎所有的强化学习算法上了一个增强buff,所以这篇论文已经入选了首届强化学习会议(RLC 2024)&a…...

mac 修改启动图图标数量
调整每行显示图标数量: defaults write com.apple.dock springboard-rows -int 7 调整每列显示的数量 defaults write com.apple.dock springboard-columns -int 8 最后重置一下启动台 defaults write com.apple.dock ResetLaunchPad -bool TRUE;killall Dock 其…...

网站架构知识之Ansible进阶(day022)
1.handler触发器 应用场景:一般用于分发配置文件时候,如果配置文件有变化,则重启服务,如果没有变化,则不重启服务 案列01:分发nfs配置文件,若文件发生改变则重启服务 2.when判断 用于给ans运…...

VMware调整窗口为可以缩小但不改变显示内容的大小
也就是缩小窗口不会影响内容的大小 这样设置就好...

Vue 3 中,ref 和 reactive的区别
在 Vue 3 中,ref 和 reactive 是两种用于创建响应式数据的方法。它们有一些关键的区别和适用场景。以下是它们的主要区别: ref 用途: ref 主要用于处理基本数据类型(如字符串、数字、布尔值等)以及需要单独响应的复杂…...

window 利用Putty免密登录远程服务器
1 在本地电脑用putty-gen生成密钥 参考1 参考2 2 服务器端操作 将公钥上传至Linux服务器。 复制上述公钥到服务器端的authorized_keys文件 mkdir ~/.ssh vi ~/.ssh/authorized_keys在vi编辑器中,按下ShiftInsert键或者右键选择粘贴,即可将剪贴板中的文…...

OGNL表达式
介绍 OGNL生来就是为了简化Java属性的取值,比如想根据名称name引用当前上下文环境中的对象,则直接键入即可,如果想要引用当前上下文环境中对象text的属性title,则键入text.title即可。如果想引用对象的非值属性,OGNL也…...

AI 大模型重塑软件开发流程的现状与未来展望
 大家好,我是程序员小羊! 前言: 随着AI技术,尤其是大模型的快速发展,软件开发领域正在经历深刻…...

Spring Boot 的核心注解
一、引言 Spring Boot 作为一种流行的 Java 开发框架,以其简洁高效的开发方式受到广泛关注。其中,核心注解在 Spring Boot 应用的开发中起着至关重要的作用。理解这些注解的含义和用法,对于充分发挥 Spring Boot 的优势至关重要。本文将深入剖…...

蓝桥杯备考——算法
一、排序 冒泡排序、选择排序、插入排序、 快速排序、归并排序、桶排序 二、枚举 三、二分查找与二分答案 四、搜索(DFS) DFS(DFS基础、回溯、剪枝、记忆化) 1.DFS算法(深度优先搜索算法) 深度优先搜…...

MutationObserver与IntersectionObserver的区别
今天主要是分享一下MutationObserver和IntersectionObserver的区别,希望对大家有帮助! MutationObserver 和 IntersectionObserver 的区别 MutationObserver 作用:用于监听 DOM 树的变动,包括:元素的属性、子元素列表或节点文本的…...
生产与配置
1.鲁滨孙克苏鲁经济 鲁滨孙克苏鲁经济是一种非常简单的自给自足的经济,劳动时间与休息时间总和为总的时间。 即 摘椰子的数量为劳动时间的函数 由于鲁滨孙喜欢椰子,厌恶劳动时间,因此无差异曲线表现为厌恶品的形态。 根据无差异曲线和生…...

Android Kotlin Flow 冷流 热流
在 Android 开发中,Flow 是 Kotlin 协程库的一部分,用于处理异步数据流的一个组件。本质上,Flow 是一个能够异步生产多个值的数据流,与 suspend 函数返回单个值的模式相对应。Flow 更类似于 RxJava 中的 Observable,但…...

订单日记助力“实峰科技”提升业务效率
感谢北京实峰科技有限公司选择使用订单日记! 北京实峰科技有限公司,成立于2022年,位于北京市石景区,是一家以从事生产、销售微特电机、输配电及控制设备等业务为主的企业。 在业务不断壮大的过程中,想使用一种既能提…...

如何安装和配置JDK17
教程目录 零、引言1、新特性概览2、性能优化3、安全性增强4、其他改进5、总结 一、下载安装二、环境配置三、测试验证 零、引言 JDK 17(Java Development Kit 17)是Java平台的一个重要版本,它带来了许多新特性和改进,进一步提升了…...

智能化温室大棚控制系统设计(论文+源码)
1 系统的功能及方案设计 本次智能化温室大棚控制系统的设计其系统整体结构如图2.1所示,整个系统在器件上包括了主控制器STC89C52,温湿度传感器DHT11,LCD1602液晶,继电器,CO2传感器,光敏电阻,按…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
