双指针(二)双指针到底是怎么个事
一.有效的三角形个数
有效的三角形个数

class Solution {public int triangleNumber(int[] nums) {Arrays.sort(nums);int i=0,end = nums.length-1;int count = 0;for( i = end;i>=2;i--){int left = 0;int right = i-1;while(left<right){if(nums[left]+nums[right]>nums[i]){count+=right-left;right--;}else{left++;}}}return count;}}

解析:利用双指针和数组的单调性去解决本题。
如果一个数组为[2,3,2,5,4,9,10],求有效的三角形个数,最好的做法是先排序让数组有序慢慢找规律。

对于三角形来说判断三边能否构成三角形最主要的条件是:2边之和大于第三边。
设a<b<c,如果要能构成三角形那么必须满足以下三个等式:
等式一:a+b>c
等式二:a+c>b
等式三:b+c>a
现在已知c为最大数,对于等式二和等式三来说,一个最大的数在加上一个正数肯定大于另外一个数。所以在已知a,b,c三者的关系后,对于等式二和三是恒成立的。那么只需要看等式一即可:在a>b>c是如果a+b>c那么这三边就能构成三角形。对于本题数组要想知道任意三边的大小关系先排序。
数组有序后,每次挑选最末尾的元素当c,因为末尾的的元素有序后肯定是最大值。c确定后只需要找到a和b,满足a+b>c即可。设a为left,b为right,left和right在数组上移动去找满足left+right>c的元素,这就转换为双指针问题。

a+b>c且b和c固定不动让a动:如果left+right>c,2和9相加>10,说明这2个元素是满足条件一的。让left往后移动到下一个位置,right固定不动,left增大或者不变那么left+right>c是恒成立的。所以不需要再去移动,这个区间right-left所有值满足。总结这种过程就不需要自己再去计算,直接区间长度就是所有满足的条件。

a+b>c,a,c不动,b动:上面的例子说明在a+b>c的时候,b和c不动的情况下直接计算即可,回到刚刚的起点这次让a不动。

如果a+b>c,a固定,那么让b–即可,重新计算看是否满足条件。

现在left+right<c,left固定right无论怎么移动都满足left+right<c,不满足构成三角形的条件。所以只能left++找下一个是否满足。

当left和right相遇后c固定的每种情况都统计完毕,让c–继续重复计算。

总结如果暴力求解时间复杂度为o(n^3),用双指针加单调性时间复杂度为o(n*n)。
二.LCR 179. 查找总价格为目标值的两个商品
LCR 179. 查找总价格为目标值的两个商品

class Solution {public int[] twoSum(int[] price, int target) {int left=0;int right = price.length-1;int [] tmp = new int[2];while(left<right){if(price[left]+price[right]<target){left++;}else if(price[left]+price[right]>target){right--;}else{tmp[0]=price[left];tmp[1]=price[right];return tmp;}}return null;}
}

本题还是和上一题解法一样利用有序数组的单调性:
这是一种双指针的思想。首先,对数组price设定两个指针,一个指针left指向数组的起始位置(索引为0),另一个指针right指向数组的末尾位置(索引为price.length - 1)。然后,计算这两个指针所指向元素的和(price[left]+price[right]),并与目标值target进行比较。如果这个和小于目标值target,说明当前两数之和偏小,为了增大和的值,将左指针left向右移动一位,因为数组是有序的(虽然题中未明确提及数组有序,但从算法逻辑看是基于有序数组假设的),这样下一次计算的和可能会更接近目标值。
如果这个和大于目标值target,说明当前两数之和偏大,为了减小和的值,将右指针right向左移动一位,同理,下一次计算的和可能会更接近目标值。
不断重复这个过程,直到找到两数之和等于目标值target,此时将这两个数的索引(这里是值本身,按照代码逻辑)放入结果数组tmp并返回;如果在左指针left小于右指针right的情况下始终没有找到满足条件的两数之和等于目标值target,则返回null。
三.三数之和
三数之和

class Solution {public List<List<Integer>> threeSum(int[] nums) {List<List<Integer>> list = new ArrayList<>();if(nums.length<3){return list;}Arrays.sort(nums);for(int i=0;i<nums.length-2;i++){if (i > 0 && nums[i] == nums[i - 1]) {continue;}int left = i+1;int right = nums.length-1;while(left<right){if(nums[left]+nums[right]<-nums[i]){left++;}else if(nums[left]+nums[right]>-nums[i]){right--;}else{list.add(Arrays.asList(nums[i],nums[left],nums[right]));left++;right--;while(left<right&&nums[left]==nums[left-1]){left++;}while(left<right&&nums[right]==nums[right+1]){right--;}}}}return list;}
}
题解:先排序可以更好去重。如果a+b+c=0,那么a+b=-c。所以只需要固定一个数充当c,定义2个指针去查找该指针对应下标元素的和等于-c的2个元素。
但是本题需要去重,[-1,1,1]和[1,-1,1]是一样的不能同时显示。
因为数组本来是排序后的,如果前一个元素和后一个元素一样时为了防止重复需要直接跳过,这样就能达到去重的效果。

整体思想是基于排序后的数组,通过固定一个数,然后使用双指针的方法来查找满足三数之和为0的组合。首先,对输入的数组nums进行排序。这一步是很关键的,因为排序后的数组可以让我们利用数组的单调性来进行高效的查找。然后,通过一个循环来固定第一个数(索引为i)。这里有一个优化点,如果当前的数和前一个数相同(即i > 0 && nums[i]==nums[i - 1]),就跳过这个数,以避免得到重复的结果。
对于固定的数nums[i],设置两个指针left(初始化为i + 1)和right(初始化为数组的末尾nums.length - 1)。
计算nums[left]+nums[right]与-nums[i]的关系。如果nums[left]+nums[right] < -nums[i],说明当前两数之和偏小,为了让和增大,将左指针left向右移动一位;如果nums[left]+nums[right] > -nums[i],说明当前两数之和偏大,为了让和减小,将右指针right向左移动一位。
当nums[left]+nums[right]等于 - nums[i]时,就找到了一组满足三数之和为0的组合,将这三个数添加到结果列表list中。然后,为了避免重复结果,移动指针left和right跳过相同的数(通过内层的两个while循环)。
不断重复这个过程,直到left < right这个条件不满足为止。最后返回结果列表list,这个列表包含了所有满足三数之和为0的组合。
- 假设使用上述
threeSum函数对数组{-4, -1, -1, 0, 1, 2}进行操作的分析如下- 首先,数组被排序。排序后的数组为
{-4, -1, -1, 0, 1, 2}。 - 然后进入外层循环,
i从0开始。- 当
i = 0时,nums[i]= - 4。- 此时
left = i+1 = 1,right = nums.length - 1=5。 - 计算
nums[left]+nums[right]与-nums[i]的关系。 - 第一次比较时,
nums[left]= - 1,nums[right]=2,nums[left]+nums[right]=1,-nums[i]=4。因为1 < 4,所以left指针右移,left变为2。 - 此时
nums[left]= - 1,nums[right]=2,nums[left]+nums[right]=1,仍然小于4,left继续右移变为3。 - 此时
nums[left]=0,nums[right]=2,nums[left]+nums[right]=2,小于4,left变为4。 - 此时
nums[left]=1,nums[right]=2,nums[left]+nums[right]=3,小于4,left变为5。 - 此时
left = right,这个i值下的内层循环结束。
- 此时
- 当
i = 1时,nums[i]= - 1。- 由于
i>0且nums[i]==nums[i - 1],根据代码中的去重逻辑,这个i值被跳过。
- 由于
- 当
i = 2时,nums[i]= - 1。- 此时
left = i + 1=3,right = nums.length - 1 = 5。 - 第一次比较时,
nums[left]=0,nums[right]=2,nums[left]+nums[right]=2,-nums[i]=1,因为2>1,所以right指针左移,right变为4。 - 此时
nums[left]=0,nums[right]=1,nums[left]+nums[right]=1,等于1,找到一组解{-1, 0, 1}。然后按照去重逻辑,移动left和right指针跳过相同的数。
- 此时
- 当
i = 3时,nums[i]=0。- 此时
left = i+1 = 4,right = nums.length - 1=5。 - 第一次比较时,
nums[left]=1,nums[right]=2,nums[left]+nums[right]=3,-nums[i]=0,因为3>0,所以right指针左移,right变为4。 - 此时
left = right,这个i值下的内层循环结束。
- 此时
- 当
i = 4时,nums[i]=1。- 此时
left = i+1 = 5,right = nums.length - 1=5,left = right,这个i值下的内层循环结束。
- 此时
- 当
i = 5时,i < nums.length - 2这个条件不满足,外层循环结束。
- 当
- 最后,函数返回包含找到的满足三数之和为0的组合的列表,在这个例子中是
[{-1, 0, 1}]。
- 首先,数组被排序。排序后的数组为
- 第一次去重(外层循环中的去重)
- 在
for循环中,当i > 0 && nums[i]==nums[i - 1]时,会执行continue语句跳过当前循环。
- 以数组
{-4, -1, -1, 0, 1, 2}为例。
当i = 0时,nums[i]= - 4,正常进行后续操作。
当i = 1时,nums[i]= - 1,由于i>0且nums[i]==nums[i - 1](因为nums[0]= - 4,nums[1]= - 1,此时nums[1]==nums[0]不成立,所以i = 1时正常进行内层循环操作)。
-
当i = 2时,nums[i]= - 1,此时i>0且nums[i]==nums[i - 1](因为nums[1]= - 1,nums[2]= - 1),所以直接跳过i = 2这个情况的内层循环操作。这就避免了重复使用相同的第一个数来寻找三数之和为0的组合,因为如果不跳过,可能会得到重复的结果组合。
2. 第二次去重(内层循环中的去重)
当找到一组满足nums[left]+nums[right]== - nums[i]的解后,需要对left和right指针进行调整以避免重复结果。 例如,在找到一组解后,先执行left++;right---,然后,有两个while循环来进行去重。 对于while (left < right&&nums[left]==nums[left - 1])这个循环,它的目的是在找到一组解后,将left指针向右移动,跳过所有与当前left位置元素相同的元素。这是因为如果不跳过,下一次循环可能会得到相同的组合。例如,如果数组中有连续的相同元素,如{-1, -1, 0, 1, 2},当找到{-1, 0, 1}这组解后,如果不跳过后面相同的-1,可能会再次得到{-1, 0, 1}这个组合。 同理,while (left < right&&nums[right]==nums[right + 1])这个循环是将right指针向左移动,跳过所有与当前right`位置元素相同的元素,以避免得到重复的结果组合。
四.四数之和
四数之和

class Solution {public List<List<Integer>> fourSum(int[] nums, int target) {Arrays.sort(nums);List<List<Integer>> list = new ArrayList<>();for(int i=0;i<nums.length;){for(int j=i+1;j<nums.length;){int left = j+1;int right=nums.length-1;while(left<right){if((long)target-nums[i]-nums[j]>nums[left]+nums[right]){left++;}else if((long)target-nums[i]-nums[j]<nums[left]+nums[right]){right--;}else{list.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));left++;right--;while(left<right&&nums[left]==nums[left-1]){left++;} while(left<right&&nums[right]==nums[right+1]){right--;}}}j++;while(j<nums.length&&nums[j]==nums[j-1]){j++;}}i++;while(i<nums.length&&nums[i]==nums[i-1]){i++;}}return list;}
}
本题还是和三数之和一样先排序在利用双指针求解。
三数之和是固定一个数然后求另外2个数是否为该数相反数。四数之和是固定2个数,目标值减去另外2个数的和是否等于固定的2个数的和。这里也是利用双指针。

相比于三数之和,三数之和只需要外部i去重,四数之和i和j都要去重。
- 整体思想
- 这个
fourSum方法的主要思想是在一个已排序的整数数组nums中找到四个数的组合,使得它们的和等于目标值target。- 首先,对输入的数组
nums进行排序。这是为了方便后续的操作,能够利用数组的单调性来优化查找过程。- 然后,使用多层嵌套循环来确定四个数中的前两个数。
- 外层
for循环用于确定第一个数(索引为i),并且在每次循环中进行去重操作。如果当前的数和前一个数相同(即nums[i]==nums[i - 1]),就跳过这个数,以避免得到重复的结果。
- 中层
for循环用于确定第二个数(索引为j),同样在每次循环中进行去重操作。如果当前的数和前一个数相同(即nums[j]==nums[j - 1]),就跳过这个数。- 内层
while循环用于确定后两个数(索引为left和right)。
- 在
while循环中,计算target - nums[i]-nums[j]与nums[left]+nums[right]的关系。- 如果
target - nums[i]-nums[j]>nums[left]+nums[right],说明当前后两个数之和偏小,为了让和增大,将左指针left向右移动一位。
- 如果
target - nums[i]-nums[j]<nums[left]+nums[right],说明当前后两个数之和偏大,为了让和减小,将右指针right向左移动一位。
- 当
target - nums[i]-nums[j]==nums[left]+nums[right]时,就找到了一组满足四数之和为target的组合,将这四个数添加到结果列表list中。然后,为了避免重复结果,移动指针left和right跳过相同的数(通过内层的两个while循环)。- 不断重复这个过程,直到所有可能的组合都被检查过,最后返回结果列表
list,这个列表包含了所有满足四数之和为target的组合。
- 第一次去重(外层循环中针对第一个数的去重)
- 思想是在确定四数之和中的第一个数时,避免使用相同的数多次作为第一个数来构建组合。因为如果不进行去重,可能会得到重复的四数组合结果。例如,数组中有多个相同的数,若不处理,以这些相同数为第一个数构建的组合可能会重复。通过比较当前数与前一个数是否相同(在已经排序的数组中),如果相同就跳过当前数,从而保证每个不同的数作为第一个数只被使用一次来构建组合。
- 第二次去重(中层循环中针对第二个数的去重)
- 当确定了第一个数之后,在确定第二个数时进行去重。由于数组是排序的,在确定第二个数时,如果当前数和前一个数相同,那么以这个数为第二个数构建的四数组合会与之前以相同的第一个数和前一个相同的第二个数构建的组合重复。所以通过比较当前数(作为第二个数)与前一个数是否相同,相同则跳过,这样可以确保对于每个确定的第一个数,不同的第二个数只会被使用一次来构建组合,避免了重复的组合结果。
- 第三次去重(内层循环中针对后两个数的去重)
- 在找到一组满足四数之和为目标值的组合后,针对确定后两个数(
left和right指向的数)的指针进行去重。当找到一组解后,如果不进行去重,下一次循环可能会因为left或者right指针没有移动到新的数而得到相同的组合。例如,数组中存在连续相同的数,在找到一组解后,如果left指针没有跳过相同的数,下一次循环可能会再次得到相同的组合。通过比较当前left(或right)指针指向的数与前一个(或后一个)数是否相同,相同则移动指针跳过,从而避免得到重复的组合结果。
- 在找到一组满足四数之和为目标值的组合后,针对确定后两个数(
相关文章:

双指针(二)双指针到底是怎么个事
一.有效的三角形个数 有效的三角形个数 class Solution {public int triangleNumber(int[] nums) {Arrays.sort(nums);int i0,end nums.length-1;int count 0;for( i end;i>2;i--){int left 0;int right i-1;while(left<right){if(nums[left]nums[right]>nums…...

vscode通过remote-ssh连接远程开发机
文章目录 安装扩展注意事项:tips其他参数安装扩展 安装VS Code和SSH-Remote扩展:首先,需要确保你已经在本地计算机上安装了VS Code,并且在扩展市场中搜索并安装了"Remote - SSH"扩展。配置SSH:在本地计算机上,打开VS Code的命令面板(使用快捷键"Ctrl+Shi…...

uniapp实现H5和微信小程序获取当前位置(腾讯地图)
之前的一个老项目,使用 uniapp 的 uni.getLocation 发现H5端定位不准确,比如余杭区会定位到临平区,根据官方文档初步判断是项目的uniapp的版本太低。 我选择的方式不是区更新uniapp的版本,是直接使用高德地图的api获取定位。 1.首…...

SQL HAVING子句
SQL 是一种基于“面向集合”思想设计的语言。HAVING 子句是一个聚合函数,用于过滤分组结果。 1 实践 1.1 缺失的编号 图 连续编号记录表t_seq_record 需求:判断seq 列编号是否有缺失。 SELECT 存在缺失的编号 AS res FROM t_seq_record HAVING COUN…...

计算机视觉基础:OpenCV库详解
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 计算机视觉基础:OpenCV库详解 计算机视觉基础:OpenCV库详解 计算机视觉基础:OpenCV库详解 引…...
UI自动化测试工具(超详细总结)
🍅 点击文末小卡片 ,免费获取软件测试全套资料,资料在手,涨薪更快 常用工具 1、QTP:商业化的功能测试工具,收费,可用于web自动化测试 2、Robot Framework:基于Python可扩展的关…...

AJAX 全面教程:从基础到高级
AJAX 全面教程:从基础到高级 目录 什么是 AJAXAJAX 的工作原理AJAX 的主要对象AJAX 的基本用法AJAX 与 JSONAJAX 的高级用法AJAX 的错误处理AJAX 的性能优化AJAX 的安全性AJAX 的应用场景总结与展望 什么是 AJAX AJAX(Asynchronous JavaScript and XML…...

ONLYOFFICE 8.2测评:功能增强与体验优化,打造高效办公新体验
引言 随着数字化办公需求的不断增长,在线办公软件市场竞争愈加激烈。在众多办公软件中,ONLYOFFICE 无疑是一个颇具特色的选择。它不仅支持文档、表格和演示文稿的在线编辑,还通过开放的接口与强大的协作功能,吸引了众多企业和个人…...

Science Robotics 综述揭示演化研究新范式,从机器人复活远古生物!
在地球46亿年的漫长历史长河中,生命的演化过程充满着未解之谜。如何从零散的化石证据中还原古生物的真实面貌?如何理解关键演化节点的具体过程?10月23日,Science Robotics发表重磅综述,首次系统性提出"古生物启发…...

uni-app表格带分页,后端处理过每页显示多少条
uni-app表格带分页,后端处理过每页可以显示多少条,一句设置好了每页显示的数据量,不需要钱的在进行操作,在进行对数据的截取 <th-table :column"column" :listData"data" :checkSort"checkSort"…...
_262)
基于STM32设计的矿山环境监测系统(NBIOT)_262
文章目录 一、前言1.1 项目介绍【1】开发背景【2】研究的意义【3】最终实现需求【4】项目硬件模块组成1.2 设计思路【1】整体设计思路【2】上位机开发思路1.3 项目开发背景【1】选题的意义【2】摘要【3】国内外相关研究现状【5】参考文献1.4 开发工具的选择【1】设备端开发【2】…...

【初阶数据结构与算法】线性表之链表的分类以及双链表的定义与实现
文章目录 一、链表的分类二、双链表的实现1.双链表结构的定义2.双链表的初始化和销毁初始化函数1初始化函数2销毁函数 3.双链表的打印以及节点的申请打印函数节点的申请 4.双链表的头插和尾插头插函数尾插函数 5.双链表的查找和判空查找函数判空函数 6.双链表的头删和尾删头删函…...

219页华为供应链管理:市场预测SOP计划、销售预测与存货管理精要
一、华为ISC供应链管理 华为的集成供应链(ISC)领先实践和SISC(Siyuan Integrated Supply Chain)架构体现了其在供应链管理领域的深度和广度,以下是7点关键介绍: 全面的供应链视野:华为ISC涵盖…...

mac 安装指定的node和npm版本
mac 安装指定的node和npm版本 0.添加映像: export N_NODE_MIRRORhttps://npmmirror.com/mirrors/node 1、使用 npm 全局安装 n npm install -g n 如果报了sudo chown -R 502:20 "/Users/xxx/.npm" sudo npm install -g n 2、根据需求安装指定版本的 node …...
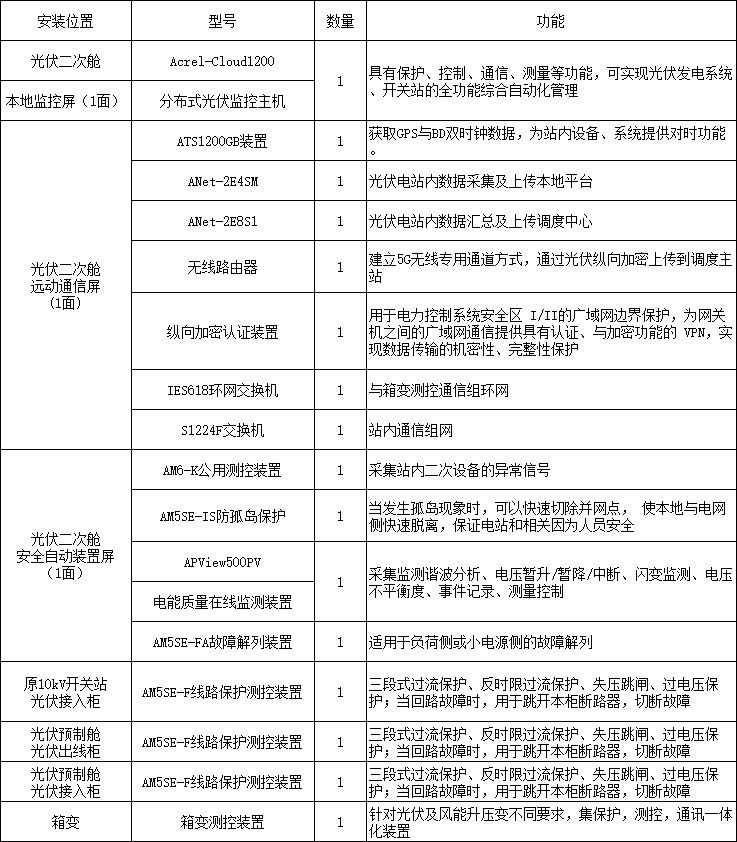
为什么分布式光伏规模是6MW为界点?
安科瑞 Acrel-Tu1990 最近,能源局颁布了一项规定,明确指出6兆瓦(MW)及以上的分布式光伏电站必须实现自发自用,自行消纳电力。多个省份的能源局进一步规定,规模超过6兆瓦的电站需按照集中式管理进行操作。此…...

arm64架构的linux 配置vm_page_prot方式
在 ARM64 架构上,通过 vm_page_prot 属性可以修改 UIO 映射内存的访问权限及缓存策略,常见的有非缓存(Non-cached)、写合并(Write Combine)等。下面是 ARM64 常用的 vm_page_prot 设置及其对应的操作方式。…...

vue3 + naive ui card header 和 title 冲突 bug
背景描述 最近发现一个 naive ui 上的问题,之前好好的,某一次升级后就出现了一个 bug,Modal 使用 card 布局后,Header Solt 下面的内容不见了,变成了 title,因为这个 solt 里面是有操作 action 的…...

Ubuntu 22.04.5 LTS配置 bond
本次纯实验,不会讲解bond功能,配置bond mode 1 和 mode 4 如何配置 确定内核模块是否加载 实验使用root用户权限,非root用户使用sudo 调用root权限 rootubuntu22:~# lsmod | grep bonding rootubuntu22:~# modprobe bonding rootubuntu22:~# …...

100种算法【Python版】第58篇——滤波算法之卡尔曼滤波
本文目录 1 算法步骤2 算法示例2.1 示例描述2.2 python代码3 算法应用:二维运动目标跟踪问题滤波算法是用于从信号中提取有用信息、去除噪声或估计系统状态的技术。在时间序列分析、信号处理和控制系统中,滤波算法起着关键作用。 1 算法步骤 卡尔曼滤波(Kalman Filter)的…...
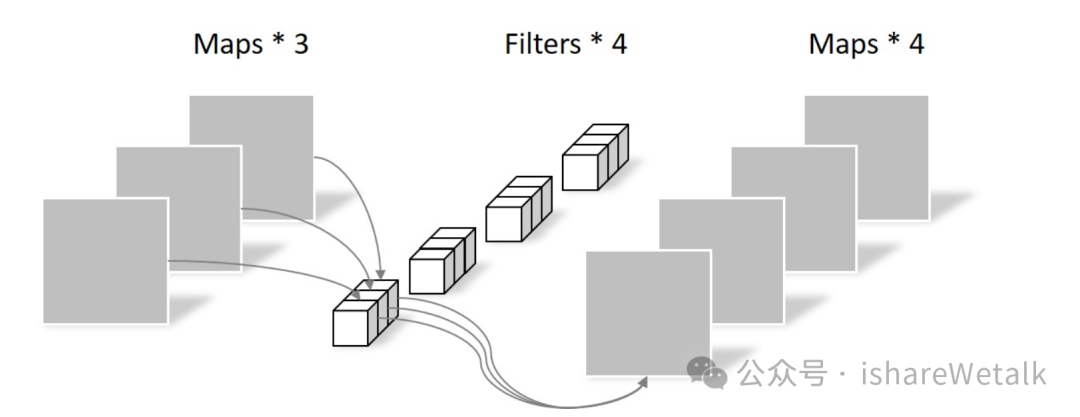
关于几种卷积
1*1卷积 分组卷积&深度可分离卷积 空洞卷积、膨胀卷积 转置卷积 https://zhuanlan.zhihu.com/p/80041030 https://yinguobing.com/separable-convolution/#fn2 11的卷积可以理解为对通道进行加权,对于一个通道来说,每个像素点加权是一样的&am…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

