卡尔曼滤波器
卡尔曼滤波器概述
卡尔曼滤波器(Kalman Filter)是一种递归的最优估计方法,广泛应用于信号处理、控制理论、导航定位等领域。它基于线性动态系统模型,通过观测数据不断更新系统的状态估计,从而使得估计值能够在噪声干扰下逐步逼近真实值。卡尔曼滤波器的关键特点是其能够在噪声不确定性较大的情况下,估计系统的状态并最小化估计误差。
卡尔曼滤波器的数学模型
卡尔曼滤波器基于线性系统的状态空间模型,其核心思想是通过对系统的动态方程进行建模,结合观测值,不断更新状态估计。基本的数学模型可以表示为以下两组方程:
-
状态转移方程(系统方程):
x k = A ⋅ x k − 1 + B ⋅ u k + w k x_k = A \cdot x_{k-1} + B \cdot u_k + w_k xk=A⋅xk−1+B⋅uk+wk- x k x_k xk:系统在时刻 k k k 的状态(例如位置、速度等)。
- A A A:状态转移矩阵,描述如何从前一时刻的状态 x k − 1 x_{k-1} xk−1 计算当前时刻的状态 x k x_k xk。
- B B B:控制输入矩阵,描述控制输入 u k u_k uk 对系统状态的影响。
- u k u_k uk:控制输入(例如,外部推动力或加速度)。
- w k w_k wk:过程噪声,通常假设其是高斯分布,均值为 0 0 0,协方差为 Q Q Q。
-
观测方程:
z k = H ⋅ x k + v k z_k = H \cdot x_k + v_k zk=H⋅xk+vk- z k z_k zk:时刻 k k k的观测值。
- H H H:观测矩阵,描述如何通过状态 x k x_k xk 得到观测值 z k z_k zk。
- v k v_k vk:测量噪声,通常假设其是高斯分布,均值为0,协方差为 R R R。
卡尔曼滤波器的过程
卡尔曼滤波器的工作过程包括两个主要步骤:预测和更新。
1. 预测步骤(Time Update)
在预测步骤中,基于当前的状态估计和控制输入,预测下一时刻的状态和误差协方差。
-
状态预测:
x ^ k − = A ⋅ x ^ k − 1 + B ⋅ u k \hat{x}_k^- = A \cdot \hat{x}_{k-1} + B \cdot u_k x^k−=A⋅x^k−1+B⋅uk
其中, x ^ k − \hat{x}_k^- x^k− 表示时刻 k k k 的预测状态(先验估计)。 -
误差协方差预测:
P k − = A ⋅ P k − 1 ⋅ A T + Q P_k^- = A \cdot P_{k-1} \cdot A^T + Q Pk−=A⋅Pk−1⋅AT+Q
其中, P k − P_k^- Pk− 表示时刻 k k k的预测误差协方差, P k − 1 P_{k-1} Pk−1 为上一时刻的误差协方差, Q Q Q 为过程噪声的协方差矩阵。
2. 更新步骤(Measurement Update)
在更新步骤中,通过观测数据更新预测的状态和误差协方差。
-
卡尔曼增益计算:
K k = P k − ⋅ H T ⋅ ( H ⋅ P k − ⋅ H T + R ) − 1 K_k = P_k^- \cdot H^T \cdot (H \cdot P_k^- \cdot H^T + R)^{-1} Kk=Pk−⋅HT⋅(H⋅Pk−⋅HT+R)−1
卡尔曼增益 (K_k) 计算了如何平衡预测值和测量值的相对可信度。较大的增益表示测量数据更可靠,较小的增益表示模型预测值更可靠。 -
状态更新:
x ^ k = x ^ k − + K k ⋅ ( z k − H ⋅ x ^ k − ) \hat{x}_k = \hat{x}_k^- + K_k \cdot (z_k - H \cdot \hat{x}_k^-) x^k=x^k−+Kk⋅(zk−H⋅x^k−)
更新后的状态估计 x ^ k \hat{x}_k x^k 结合了预测值和观测值。 -
误差协方差更新:
P k = ( I − K k ⋅ H ) ⋅ P k − P_k = (I - K_k \cdot H) \cdot P_k^- Pk=(I−Kk⋅H)⋅Pk−
更新后的误差协方差 P k P_k Pk 反映了当前状态估计的不确定性。
卡尔曼滤波器的基本流程
卡尔曼滤波器的基本过程包括初始化、预测和更新三个阶段。下面是完整的卡尔曼滤波步骤:
-
初始化:
- 给定初始状态估计值 x ^ 0 \hat{x}_0 x^0 和初始误差协方差矩阵 P 0 P_0 P0。
-
预测:
- 根据状态转移方程预测下一时刻的状态: x ^ k − = A ⋅ x ^ k − 1 + B ⋅ u k \hat{x}_k^- = A \cdot \hat{x}_{k-1} + B \cdot u_k x^k−=A⋅x^k−1+B⋅uk
- 预测误差协方差: P k − = A ⋅ P k − 1 ⋅ A T + Q P_k^- = A \cdot P_{k-1} \cdot A^T + Q Pk−=A⋅Pk−1⋅AT+Q
-
更新:
- 计算卡尔曼增益: K k = P k − ⋅ H T ⋅ ( H ⋅ P k − ⋅ H T + R ) − 1 K_k = P_k^- \cdot H^T \cdot (H \cdot P_k^- \cdot H^T + R)^{-1} Kk=Pk−⋅HT⋅(H⋅Pk−⋅HT+R)−1
- 更新状态估计: x ^ k = x ^ k − + K k ⋅ ( z k − H ⋅ x ^ k − ) \hat{x}_k = \hat{x}_k^- + K_k \cdot (z_k - H \cdot \hat{x}_k^-) x^k=x^k−+Kk⋅(zk−H⋅x^k−)
- 更新误差协方差: P k = ( I − K k ⋅ H ) ⋅ P k − P_k = (I - K_k \cdot H) \cdot P_k^- Pk=(I−Kk⋅H)⋅Pk−
卡尔曼滤波器的应用
卡尔曼滤波器被广泛应用于多个领域,特别是在控制系统、信号处理、导航与定位、自动驾驶等领域。
-
导航定位( G P S / I M U GPS/IMU GPS/IMU):
- 在自动驾驶、无人机定位等领域,卡尔曼滤波器用来融合来自多个传感器的数据(如 GPS、IMU、里程计等),实现更精确的位置估计。
-
图像处理与目标跟踪:
- 在计算机视觉中,卡尔曼滤波器常用于动态物体的跟踪,例如人脸追踪、运动目标预测等。
-
金融数据分析:
- 在金融领域,卡尔曼滤波器用于估计股票价格、市场波动等。
-
信号处理:
- 卡尔曼滤波器可以用于去除噪声,平滑信号,从而得到更准确的结果。
卡尔曼滤波器的优势
-
递归性:
- 卡尔曼滤波器是递归的,不需要存储所有历史数据,每次仅依赖当前的状态估计和观测数据即可更新状态。
-
最优性:
- 在假设过程噪声和测量噪声符合高斯分布的情况下,卡尔曼滤波器能够提供最优估计,最小化估计误差的均方误差( M S E MSE MSE)。
-
实时性:
- 卡尔曼滤波器适用于实时数据处理,可以在每一时刻获得最新的状态估计。
卡尔曼滤波器的局限性
-
线性假设:
- 标准卡尔曼滤波器假设系统是线性的,但许多实际问题是非线性的。对于非线性系统,通常需要扩展卡尔曼滤波器( E K F EKF EKF)或无迹卡尔曼滤波器( U K F UKF UKF)。
-
噪声假设:
- 卡尔曼滤波器假设过程噪声和测量噪声是高斯分布的。在某些应用中,噪声可能不符合高斯分布,这会影响滤波器的效果。
-
状态与观测的建模问题:
- 卡尔曼滤波器需要准确的系统模型,包括状态转移方程、观测方程以及噪声协方差。如果模型不准确,滤波效果会较差。
总结
卡尔曼滤波器是一种强大的工具,广泛应用于估计和预测动态系统的状态。它能够在噪声干扰下提供最优估计,并且具有递归性和实时性。然而,它对于线性系统和高斯噪声假设的依赖使得在某些非线性或噪声非高斯分布的情况下,可能需要采用扩展卡尔曼滤波器( E K F EKF EKF)等其他变种。
相关文章:

卡尔曼滤波器
卡尔曼滤波器概述 卡尔曼滤波器(Kalman Filter)是一种递归的最优估计方法,广泛应用于信号处理、控制理论、导航定位等领域。它基于线性动态系统模型,通过观测数据不断更新系统的状态估计,从而使得估计值能够在噪声干扰…...

基于BERT的情感分析
基于BERT的情感分析 1. 项目背景 情感分析(Sentiment Analysis)是自然语言处理的重要应用之一,用于判断文本的情感倾向,如正面、负面或中性。随着深度学习的发展,预训练语言模型如BERT在各种自然语言处理任务中取得了…...

推荐15个2024最新精选wordpress模板
以下是推荐的15个2024年最新精选WordPress模板,轻量级且SEO优化良好,适合需要高性能网站的用户。中文wordpress模板适合搭建企业官网使用。英文wordpress模板,适合B2C网站搭建,功能强大且兼容性好,是许多专业外贸网站的…...

AWTK-WIDGET-WEB-VIEW 实现笔记 (2) - Windows
在 Windows 平台上的实现,相对比较顺利,将一个窗口嵌入到另外一个窗口是比较容易的事情。 1. 创建窗口 这里有点需要注意: 父窗口的大小变化时,子窗口也要跟着变化,否则 webview 显示不出来。创建时窗口的大小先设置…...

Linux四剑客及正则表达式
正则表达式 基础正则(使用四剑客命令时无需加任何参数即可使用) ^ # 匹配以某一内容开头 如:^grep匹配所有以grep开头的行。 $ # 匹配以某一内容结尾 如:grep$ 匹配所有以grep结尾的行。 ^$ # 匹配空行。 . # 匹配…...
ALS 推荐算法案例演示(python)
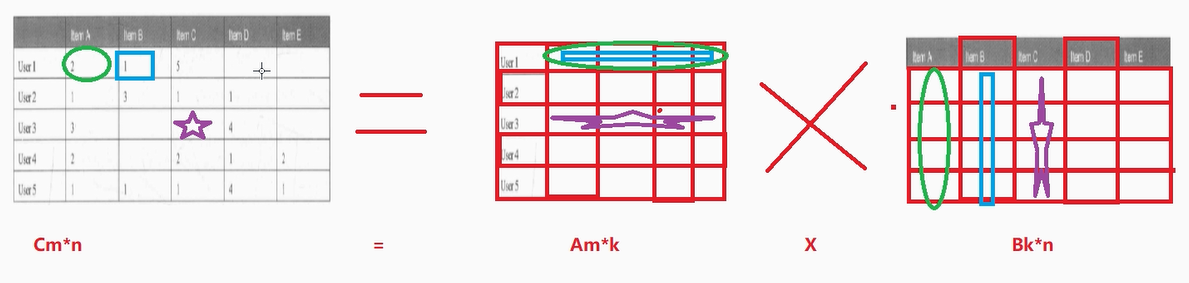
数学知识补充:矩阵 总结来说: Am*k X Bk*n Cm*n ----至于乘法的规则,是数学问题, 知道可以乘即可,不需要我们自己计算 反过来 Cm*n Am*k X Bk*n ----至于矩阵如何拆分/如何分解,是数学问题,知道可以拆/可以分解即可 ALS 推荐算法案例:电影推…...

labview中连接sql server数据库查询语句
当使用数据库查询功能时,我们需要用到数据库的查询语句,这里已调用sql server为例,我们需要按照时间来查询,这里在正常调用数据库查询语句时,我们需要在前面给他加一个限制条件这里用到了,数据库的查询语句…...

leetcode_二叉树最大深度
对二叉树的理解 对递归调用的理解 对内存分配的理解 基础数据结构(C版本) - 飞书云文档 每次函数的调用 都会进行一次新的栈内存分配 所以lmax和rmax的值不会混在一起 /*** Definition for a binary tree node.* struct TreeNode {* int val;* …...

Elasticsearch 重建索引 数据迁移
Elasticsearch 重建索引 数据迁移 处理流程创建临时索引数据迁移重建索引写在最后 大家都知道,es的索引创建完成之后就不可以再修改了,包括你想更改字段属性或者是分词方式等。那么随着业务数据量的发展,可能会出现需要修改索引,或…...

2411rust,异步函数
原文 Rust异步工作组很高兴地宣布,在实现在特征中使用异步 fn的目标方面取得了重大进度.将在下周发布稳定的Rust1.75版,会包括特征中支持impl Trait注解和async fn. 稳定化 自从RFC#1522在Rust1.26中稳定下来以来,Rust就允许用户按函数的返回类型(一般叫"RPIT")编…...

前端网络性能优化问题
DNS预解析 DNS 解析也是需要时间的,可以通过预解析的⽅式来预先获得域名所对应的 IP。 <link rel"dns-prefetch" href"//abcd.cn"> 缓存 强缓存 在缓存期间不需要请求, state code 为 200 可以通过两种响应头实现&#…...

优选算法——双指针
前言 本篇博客为大家介绍双指针问题,它属于优选算法中的一种,也是一种很经典的算法;算法部分的学习对我们来说至关重要,它可以让我们积累解题思路,同时也可以大大提升我们的编程能力,本文主要是通过一些题…...

【Rabbitmq篇】RabbitMQ⾼级特性----消息确认
目录 前言: 一.消息确认机制 • ⾃动确认 • ⼿动确认 手动确认方法又分为三种: 二. 代码实现(spring环境) 配置相关信息: 1). AcknowledgeMode.NONE 2 )AcknowledgeMode.AUTO 3&…...
开源TTS语音克隆神器GPT-SoVITS_V2版本地整合包部署与远程使用生成音频
文章目录 前言1.GPT-SoVITS V2下载2.本地运行GPT-SoVITS V23.简单使用演示4.安装内网穿透工具4.1 创建远程连接公网地址 5. 固定远程访问公网地址 前言 本文主要介绍如何在Windows系统电脑使用整合包一键部署开源TTS语音克隆神器GPT-SoVITS,并结合cpolar内网穿透工…...

【idea】更换快捷键
因为个人习惯问题需要把快捷键替换一下。我喜欢用CTRLD删除一下,用CTRLY复制一样。恰好这两个快捷键需要互换一下。 打开file——>setting——>Keymap——>Edit Actions 找到CTRLY并且把它删除 找到CTRLD 并且把它删除 鼠标右键添加CTRLY 同样操作在Delet…...

最小的子数组(leetcode 209)
给定一个正整数数组,找到大于等于s的连续的最小长度的区间。 解法一:暴力解法 两层for循环,一个区间终止位置,一个区间起始位置,找到大于等于s的最小区间长度(超时了) 解法二:双指…...

IDEA-Plugins无法下载插件(网络连接问题-HTTP Proxy Settings)
IDEA-Plugins无法下载插件(网络连接问题) 改成如下配置: 勾选 添这个url即可:https://plugins.jetbrains.com/ 重启插件中心,问题解决。...

AWTK-WIDGET-WEB-VIEW 发布
awtk-widget-web-view 是通过 webview 提供的接口,实现的 AWTK 自定义控件,使得 AWTK 可以方便的显示 web 页面。 项目网址: https://gitee.com/zlgopen/awtk-widget-web-view webview 提供了一个跨平台的 webview 接口,是一个非…...

Mysql每日一题(if函数)
两种写法if()和case if()函数 select *,if(T.xT.y>T.z and T.xT.z>T.y and T.yT.z>T.x,Yes,No) as triangle from Triangle as T; case方法 select *, case when T.xT.y>T.z and T.xT.z>T.y and T.yT.z>T.x then Yes else No end as triangle from Trian…...

Spring Cloud Alibaba [Gateway]网关。
1 简介 网关作为流量的入口,常用功能包括路由转发、权限校验、限流控制等。而springcloudgateway 作为SpringCloud 官方推出的第二代网关框架,取代了Zuul网关。 1.1 SpringCloudGateway特点: (1)基于Spring5,支持响应…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
