【神经网络基础】
神经网络基础
- 1.损失函数
- 1.损失函数的概念
- 2.分类任务损失函数-多分类损失:
- 3.分类任务损失函数-二分类损失:
- 4.回归任务损失函数计算-MAE损失
- 5.回归任务损失函数-MSE损失
- 6.回归任务损失函数-Smooth L1损失
- 2.网络优化方法
- 1.梯度下降算法
- 2.反向传播算法(BP算法)
- 3.梯度下降优化方法
- 4.学习率衰减方法
- 3.正则化方法
1.损失函数
1.损失函数的概念
什么是损失函数
在深度学习中,**损失函数是用来衡量模型参数质量的函数,**衡量方式是比较网络输出和真实输出之间的差异.

不同文献中有不同命名方式
loss function:损失函数
cost function:代价函数
objective function:目标函数
error function:误差函数
2.分类任务损失函数-多分类损失:
使用nn.CrossEntropyLoss()计算交叉熵损失值
多分类任务中通常使用softmax将logits(逻辑值)转换为概率形式,多分类的交叉熵损失也叫softmax 损失,计算方法是
L = − ∑ i = 1 n y i l o g ( f θ ( X i ) ) L = -\sum_{i=1}^n{y_i}{log(f_θ(X_i))} L=−i=1∑nyilog(fθ(Xi))
y是样本x属于某一个类别的真实概率
而f(x)是样本属于某一个类别的预测分数
s为softmax激活函数,将属于莫一类别的预测分数转换成概率
L是用来衡量真实值y与预测值f(x)之间差异性的损失结果
计算 L交叉熵的值越小越与真实值更加接近

在Python中实现使用nn.CrossEntropyLoss()如下所示:
# 构建多分类损失函数-CrossEntropy
import torch
from torch import nn# 多分类任务交叉熵损失:使用nn.CrossEntropyLoss()实现
def test01():# 设置真实值:可以是热编码后的结果也可以不是y_true = torch.tensor([[0, 1, 0], [0, 0, 1]], dtype=torch.float32)# 注意的类别必须是64为整数型# y_true = torch.tensor([1, 2], dtype=torch.int64)# 构建预测值计算损失结果y_pred = torch.tensor([[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]], dtype=torch.float32)# 实例化交叉熵损失loss = nn.CrossEntropyLoss()# 计算损失结果:默认情况下,CrossEntropyLoss()会自动将预测值进行one-hot编码。# 转换为numpy类型my_loss = loss(y_pred, y_true).numpy()print('loss', my_loss)
3.分类任务损失函数-二分类损失:
使用nn.BCELoss()计算二分类交叉熵
在处理二分类任务时使用sigmoid激活函数,使用二分类的交叉熵损失函数:
L = − y l o g y ^ − ( 1 − y ) l g ( 1 − y ^ ) L = -ylog\hat y - (1-y)lg(1-\hat y) L=−ylogy^−(1−y)lg(1−y^)
- y样本x属于某一个类别的真实概率
- 而y^是样本属于某一类别的预测概率
- L是衡量真实值与预测值之间差异性的损失结果
在Python实现nn.BCELoss()结果:如下所示
# 2-二分类-BCELoss.py
import torch
from torch import nndef test01():# 1.设置真实值与预测值# 预测值为sigmoid()函数的输出结果# requires_grad=True:表示需要计算梯度,用于反向传播。y_pred = torch.tensor([0.6901, 0.5459, 0.2469], requires_grad=True)y_true = torch.tensor([0, 1, 0], dtype=torch.float32)# 2.实例化二分类交叉熵loss = nn.BCELoss()# 3,计算损失值# 在 PyTorch 中,如果一个张量需要梯度(即 requires_grad=True),# 则不能直接调用 .numpy() 方法,因为这会导致梯度信息丢失,从而影响反向传播# 需要使用 .detach() 方法my_loss = loss(y_pred, y_true).detach().numpy()print('loss', my_loss)
4.回归任务损失函数计算-MAE损失
Mean absolute loss (MAE)被称为L1 Loss,以绝对误差作为距离,损失函数公式
L = 1 n ∑ i = 1 n ∣ y i − f θ ( x i ) ∣ L = \frac{1}{n}\sum_{i=1}^n|y_i-f_θ(x_i)| L=n1i=1∑n∣yi−fθ(xi)∣
曲线图如下:

特点是
-
1.由于 LI Loss具有稀疏性,为了惩罚较大的值常作为正则化添加到其他loss中作为约束
-
2. L1 Loss最大问题就是零点梯度不平滑,导致会跳过极小值
在python中实现使用nn.L1Loss()实现
import torch
from torch import nndef test01():# 1.设置真实值与预测值# requires_grad=True:表示需要计算梯度,前向传播会记录梯度,用于反向传播。y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)y_true = torch.tensor([2.0, 2.0, 2.9], dtype=torch.float32)# 2.实例化MAE损失对象loss = nn.L1Loss()# 3.计算损失my_loss = loss(y_pred,y_true).detach().numpy()print('loss',my_loss)
if __name__ == '__main__':test01()
5.回归任务损失函数-MSE损失
MSE:L2 Loss 损失或者叫欧式距离,以误差的平方和的均值作为距离
损失公式
L = 1 n ∑ i = 1 n ( y i − f θ ( x i ) ) 2 L = \frac{1}{n}\sum_{i=1}^n(y_i-fθ(x_i))^2 L=n1i=1∑n(yi−fθ(xi))2
曲线图如下:

特点是:
1.L2 loss也常作为正则化项
2.当预测值与目标值相差较大时,梯度容易发生爆炸
在 python中使用nn.MSELoss()实现,如下所示
import torch
from torch import nndef test01():# 1.设置真实值与预测值y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)# 2.实例化MSE损失对象loss = nn.MSELoss()# 3.计算损失my_loss = loss(y_pred, y_true).detach().numpy()print('loss', my_loss)if __name__ == '__main__':test01()
6.回归任务损失函数-Smooth L1损失
smooth L1说的是光滑之后的L1,损失函数公式:
s m o o t h L 1 ( x ) = { 0.5 ( x ) 2 if ∣ x ∣ < 1 ∣ x ∣ − 0.5 otherwise smooth_{L1}(x) = \begin{cases} 0.5(x )^2 & \text{if } |x | < 1 \\ |x | - 0.5 & \text{otherwise} \end{cases} smoothL1(x)={0.5(x)2∣x∣−0.5if ∣x∣<1otherwise
x = f(x) - y 为真实值 和 预测值之间的差值
从下图可以看出该函数实际为一个分段函数
1.在区间[-1,1]实际是L2损失,解决了L1不光滑问题
2.在区间[-1,1]外,实际就是L1损失,这就解决离群点爆炸问题

在python中使用 nn.SmoothL1Loss()实现,如下所示
import torch
from torch import nndef test01():# 1.设置真实值与预测值y_pred = torch.tensor([0.6, 0.4], requires_grad=True)y_true = torch.tensor([0, 3])# 2.实例化SmoothL1损失对象loss = nn.SmoothL1Loss()# 3.计算损失# detach():将损失张量从计算图中分离出来,不影响梯度计算my_loss = loss(y_pred, y_true).detach().numpy()print('loss', my_loss)if __name__ == '__main__':test01()
2.网络优化方法
1.梯度下降算法
梯度下降法是一种寻找使损失函数最小化的方法,从数学的角度看,梯度方向是函数增长最快的方向, 梯度的反方向就是函数减少最快的方向,所以有:
W i j n e w = W i j o i d − α ∂ E ∂ W i j W_{ij}^{new} = W_{ij}^{oid} - α\frac{∂E}{∂W_{ij}} Wijnew=Wijoid−α∂Wij∂E
其中α为学习率,如果学习率太小,得到的效果就太小,增大训练成本.学习率太大可能跳过最优解,解决方法是,让学习率需要需要随着训练的进行而变化.

在进行模型训练时,有三个基础概念:
-
Epoch:使用全部数据对模型进行完整的训练,训练轮次
-
Batch_size:使用 训练集中小部分样本对模型权重进行以此反向传播的参数的更新,每次训练每批次的数据
-
Iteration:使用一个Batch的数据对模型进行一次参数的更新的过程
# 假设数据集有 50000 个训练样本,现在选择 Batch Size = 256 对模型进行训练。- 每个 Epoch 要训练的图片数量:50000- 训练集具有的 Batch 个数:50000/256+1=196- 每个 Epoch 具有的 Iteration 个数:196- 10个 Epoch 具有的 Iteration 个数:1960
在深度学习过程中,梯度下降的几种方式根本区别在于Batch_size的不同,如下表所示:

注:上表中Mini-Batch的Batch个数为N/B+1是针对未整除的情况,整除则是N/B
2.反向传播算法(BP算法)
**前向传播:**指的是数据输入的神经网络中,逐层向前传输,一直=运输到输出层为止
**反向传播:利用损失函数从后往前,结合梯度下降算法,**依次对各个参数的偏导,并进行参数更新

**反向传播对神经网络中的各个节点的权重进行更新.**一个简单的神经网络 用来举例:激活函数为sigmoid

前向传播运算过程:

反向传播:我们先来求最简单的,求误差E对w5的导数。要求误差E对w5的导数,需要先求误差E对out o1的导数,再求out o1对net o1的导数,最后再求net o1对w5的导数,经过这个处理,我们就可以求出误差E对w5的导数(偏导),如下图所示:

导数(梯度)计算出来,下面就是反向传播与参数更新过程:

如果要想求误差E对W1的导数,误差E对W1的求导路径不止一条,计算过程如图所示:

- 代码实现
# 构建神经元网络
# 导入数据包
import torch
# 导入神经元nn模块
import torch.nn as nn
# 优化器
from torch import optim# 创建神经元网络类
class Model(nn.Module):# 初始化两个方法# 初始化参数def __init__(self):# 调用父类初始化方法super(Model, self).__init__()# 构建网络层self.linear1 = nn.Linear(2, 2)self.linear2 = nn.Linear(2, 2)# 初始化权重参数nn.init.kaiming_normal_(self.linear1.weight)nn.init.xavier_normal_(self.linear2.weight)# 前向传播def forward(self, x):# 数据经过第一层网络x = self.linear1(x)# 计算第一层激活值x = torch.relu(x)# 数据经过第二层网络x = self.linear2(x)# 计算第二层激活值x = torch.sigmoid(x)return xif __name__ == '__main__':# 定义输入值和目标值inputs = torch.tensor([[0.05, 0.10]])target = torch.tensor([0.01, 0.99])# 实例化神经元网络对象model = Model()# 预测值output = model(inputs)# 计算误差loss = nn.MSELoss()my_loss = loss(output, target)print('loss', my_loss)# 优化方法和反向传播方法optimizer = optim.SGD(model.parameters(), lr=1e-2)optimizer.zero_grad()# 自己计算的损失函数进行反向传播my_loss.backward()print('梯度', model.linear1.weight.grad)print('梯度', model.linear2.weight.grad)optimizer.step()# 打印神经网络参数# state_dict():于获取模型参数状态字典的方法print(model.state_dict())
总结
前向传播:指的就是数据输入的神经网络中,逐层向前传输,一直运算到输出层为止
反向传播(Back Propagation):利用损失函数ERROR,从后往前,结合梯度下降算法,一次求各个参数的偏导数
3.梯度下降优化方法
梯度下降优化算法中,可能碰到以下情况:
1.碰到平缓区域,梯度值较小,参数优化变慢
2.碰到’‘鞍点’',梯度为0,参数无法优化
3.碰到局部最小值,参数不是最优
对于以下问题,出现一些梯度下降算法的优化方法,例如: Monmentum,AdaGrad,RMSprop,Adqam等.

1.指数加权平均
指数移动加权平均则是参考各数值 ,并且各数值权重都不同,距离越远的数字对平均计算贡献越小,距离越近则对平均数的计算贡献越大.
计算公式为:
S t = { Y 1 , t = 0 β ∗ S t − 1 + ( 1 − β ) ∗ Y t t>0 S_t = \begin{cases} Y_1, & \text t =0 \\ β*S_{t-1} + (1-β)*Y_t & \text{t>0} \end{cases} St={Y1,β∗St−1+(1−β)∗Ytt=0t>0
St表示指数加权平均值
Yt表示t时刻的值
β 调节权重系数,该值越大平均数越平缓
2.动量算法Momentum:
梯度计算公式:Dt = β * St-1 + (1- β) * Wt
梯度更新公式为:
St-1 表示历史梯度移动加权平均值
Wt 表示当前时刻的梯度值
Dt 为当前时刻的指数加权平均梯度值
β 为权重系数
假设:权重 β 为 0.9,例如:
- 第一次梯度值:D1 = S1 = W1
- 第二次梯度值:D2=S2 = 0.9 * S1 + W2 * 0.1
- 第三次梯度值:D3=S3 = 0.9 * S2 + W3 * 0.1
- 第四次梯度值:D4=S4 = 0.9 * S3 + W4 * 0.1
梯度下公式中的梯度计算,不在是当前时刻的t的梯度值,而是历史梯度值而历史梯度值的指数移动加权平均值,公式修改为:
W i j n e w = W i j o i d − α D t W_{ij}^{new} = W_{ij}^{oid} - αD_t Wijnew=Wijoid−αDt
Monmentum 优化方法是如何一定程度上克服 “平缓”、”鞍点” 的问题呢?

当处于鞍点位置时,由于当前的梯度为 0,参数无法更新。但是 Momentum 动量梯度下降算法已经在先前积累了一些梯度值,很有可能使得跨过鞍点
由于 mini-batch 普通的梯度下降算法,每次选取少数的样本梯度确定前进方向,可能会出现震荡,使得训练时间变长。Momentum 使用移动加权平均,平滑了梯度的变化,使得前进方向更加平缓,有利于加快训练过程。
import torch
import matplotlib.pyplot as pltdef test03():# 1 初始化权重参数w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)y = ((w ** 2) / 2.0).sum()# 2 实例化优化方法,SGD指定参数beta=0.9optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)# 3 第一次更新计算梯度,并对参数进行更新optimizer.zero_grad()y.backward()optimizer.step()print('第1次: 梯度w.grad: %f,更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))# 4 第2次更新 计算梯度,并对参数进行更新# 使用更新后的参数机选输出结果y = ((w ** 2) / 2.0).sum()optimizer.zero_grad()y.backward()optimizer.step()print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy())
3.AdaGrad:通过对不同的参数分量使用不同的学习率,AdaGrad学习率总体会逐渐减小
计算步骤如下:
import torch
import matplotlib.pyplot as pltdef test04():# 1 初始化权重参数w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)y = ((w ** 2) / 2.0).sum()# 2 实例化优化方法:adagrad优化方法optimizer = torch.optim.Adagrad([w], lr=0.01)# 3 第1次更新 计算梯度,并对参数进行更新optimizer.zero_grad()y.backward()optimizer.step()print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))# 4 第2次更新 计算梯度,并对参数进行更新# 使用更新后的参数机选输出结果y = ((w ** 2) / 2.0).sum()optimizer.zero_grad()y.backward()optimizer.step()print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))1.初始化学习率 α、初始化参数 θ、小常数 σ = 1e-6(表示为10的-6次方)
2.初始化梯度累积变量 s = 0
3.从训练集中采样 m 个样本的小批量,计算梯度 g
4.累积平方梯度 s = s + g ⊙ g,⊙ 表示各个分量相乘
学习率计算α的计算公式为:
α = α s + σ α = \frac{α}{\sqrt{s} + σ} α=s+σα
参数更新公式为:
w = w − α s + σ w = w - \frac{α}{\sqrt{s} + σ} w=w−s+σα
注:AdaGrad缺点是可能使得学习率过早,过量的降低,导致模型 训练到后期学习率太小,难以找到最优解.
4.RMSProp
RMSProp优化算法是对AdaGrad的优化,使用指数移动加权平均梯度替换历史梯度的平方和,计算如下:
# alpha=0.9 初始化β权重系数
"""
初始化学习率 α、初始化参数 θ、小常数 σ = 1e-6初始化参数 θ初始化梯度累计变量 s从训练集中采样 m 个样本的小批量,计算梯度 g使用指数移动平均累积历史梯度,
"""
公式如下:
s = β ∗ s + ( 1 − β ) g ⊙ g ( ⊙ 表示各个分量相乘 ) s = β*s + (1-β)g⊙g (⊙ 表示各个分量相乘) s=β∗s+(1−β)g⊙g(⊙表示各个分量相乘)
学习率计算公式为:
α = α s + σ α = \frac{α}{\sqrt{s} + σ} α=s+σα
参数更新公式为:
w = w − α s + σ . g w = w - \frac{α}{\sqrt{s} + σ}.g w=w−s+σα.g
import torch
import matplotlib.pyplot as pltdef test05():# 1 初始化权重参数w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)y = ((w ** 2) / 2.0).sum()# 2 实例化优化方法:RMSprop算法,其中alpha对应这betaoptimizer = torch.optim.RMSprop([w], lr=0.01, alpha=0.9)# 3 第1次更新 计算梯度,并对参数进行更新optimizer.zero_grad()y.backward()optimizer.step()print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))# 4 第2次更新 计算梯度,并对参数进行更新# 使用更新后的参数机选输出结果y = ((w ** 2) / 2.0).sum()optimizer.zero_grad()y.backward()optimizer.step()print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
5.Adam:使用动量和RMSProp来动态调整每个参数的学习率
- Momentum使用指数加权平均计算当前梯度值
- AdaGrad , RMSProp 使用自适应的学习率
- Adam优化算法将Momentum 和RMSProp算法结合一起
- 修正梯度:使用梯度的指数加权平均
- 修正学习率:使用梯度平方的指数加权平均
# 2 实例化优化方法:Adam算法,其中betas是指数加权的系数
optimizer = torch.optim.Adam([w], lr=0.01, betas=[0.9, 0.99])
4.学习率衰减方法
1.等间隔学习率衰减
学习率衰减方法-等间隔学习率衰减
如图所示

def test_StepLR():# 0.参数初始化LR = 0.1 # 设置学习率初始化值为0.1iteration = 10max_epoch = 200# 1 初始化参数y_true = torch.tensor([0])x = torch.tensor([1.0])w = torch.tensor([1.0], requires_grad=True)# 2.优化器optimizer = optim.SGD([w], lr=LR, momentum=0.9)# 3.设置学习率下降策略scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)# 4.获取学习率的值和当前的epochlr_list, epoch_list = list(), list()for epoch in range(max_epoch):lr_list.append(scheduler_lr.get_last_lr()) # 获取当前lrepoch_list.append(epoch) # 获取当前的epochfor i in range(iteration): # 遍历每一个batch数据loss = ((w*x-y_true)**2)/2.0 # 目标函数optimizer.zero_grad()# 反向传播loss.backward()optimizer.step()# 更新下一个epoch的学习率scheduler_lr.step()# 5.绘制学习率变化的曲线plt.plot(epoch_list, lr_list, label="Step LR Scheduler")plt.xlabel("Epoch")plt.ylabel("Learning rate")plt.legend()plt.show()
2.指定间隔学习率衰减
学习率优化方法-指定间隔学习率衰减
如图所示

def test_MultiStepLR():torch.manual_seed(1)LR = 0.1iteration = 10max_epoch = 200weights = torch.randn((1), requires_grad=True)target = torch.zeros((1))print('weights--->', weights, 'target--->', target)optimizer = optim.SGD([weights], lr=LR, momentum=0.9)# 设定调整时刻数milestones = [50, 125, 160]# 设置学习率下降策略scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.5)lr_list, epoch_list = list(), list()for epoch in range(max_epoch):lr_list.append(scheduler_lr.get_last_lr())epoch_list.append(epoch)for i in range(iteration):loss = torch.pow((weights - target), 2)optimizer.zero_grad()# 反向传播loss.backward()# 参数更新optimizer.step()# 更新下一个epoch的学习率scheduler_lr.step()plt.plot(epoch_list, lr_list, label="Multi Step LR Scheduler\nmilestones:{}".format(milestones))plt.xlabel("Epoch")plt.ylabel("Learning rate")plt.legend()plt.show()3.按指数学习率衰减
学习率优化方法-按指数学习率衰减
如图所示

def test_ExponentialLR():# 0.参数初始化LR = 0.1 # 设置学习率初始化值为0.1iteration = 10max_epoch = 200# 1 初始化参数y_true = torch.tensor([0])x = torch.tensor([1.0])w = torch.tensor([1.0], requires_grad=True)# 2.优化器optimizer = optim.SGD([w], lr=LR, momentum=0.9)# 3.设置学习率下降策略gamma = 0.95scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)# 4.获取学习率的值和当前的epochlr_list, epoch_list = list(), list()for epoch in range(max_epoch):lr_list.append(scheduler_lr.get_last_lr())epoch_list.append(epoch)for i in range(iteration): # 遍历每一个batch数据loss = ((w * x - y_true) ** 2) / 2.0optimizer.zero_grad()# 反向传播loss.backward()optimizer.step()# 更新下一个epoch的学习率scheduler_lr.step()# 5.绘制学习率变化的曲线plt.plot(epoch_list, lr_list, label="Multi Step LR Scheduler")plt.xlabel("Epoch")plt.ylabel("Learning rate")plt.legend()plt.show()
3.正则化方法
正则化作用:防止神经网络表示过拟合
Dropout(随机失活)
在神经网络中模型参数较多,在数据不足的情况下,容易过拟合,**Dropout(随机失活)**是一个简单有效的正则化方法.

在训练过程中,Dropout的实现是让神经元 以超参数p的概率停止工作或者 激活被置为0,未被置为0的进行缩放,缩放比例为1/(1-p)
在测试过程中,随机失活不起作用
import torch
import torch.nn as nndef test():# 初始化随机失活层dropout = nn.Dropout(p=0.4)# 初始化输入数据:表示某一层的weight信息inputs = torch.randint(0, 10, size=[1, 4]).float()layer = nn.Linear(4,5)y = layer(inputs)print("未失活FC层的输出结果:\n", y)y = dropout(y)print("失活后FC层的输出结果:\n", y)# 上述代码将 Dropout 层的概率 p 设置为 0.4,此时经过 Dropout 层计算的张量中就出现了很多 0 , 未变为0的按照(1/(1-0.4))进行处理。
相关文章:

【神经网络基础】
神经网络基础 1.损失函数1.损失函数的概念2.分类任务损失函数-多分类损失:3.分类任务损失函数-二分类损失:4.回归任务损失函数计算-MAE损失5.回归任务损失函数-MSE损失6.回归任务损失函数-Smooth L1损失 2.网络优化方法1.梯度下降算法2.反向传播算法(BP算法)3.梯度下降优化方法…...

实战 | C#中使用YoloV8和OpenCvSharp实现目标检测 (步骤 + 源码)
导 读 本文主要介绍在C#中使用YoloV8实现目标检测,并给详细步骤和代码。 详细步骤 【1】环境和依赖项。 需先安装VS2022最新版,.NetFramework8.0,然后新建项目,nuget安装 YoloSharp,YoloSharp介绍: https://github.com/dme-compunet/YoloSharp 最新版6.0.1,本文…...

debian 如何进入root
debian root默认密码, 在Debian系统中,安装完成后,默认情况下root账户是没有密码的。 你可以通过以下步骤来设置或更改root密码: 1.打开终端。 2.输入 sudo passwd root 命令。 3.当提示输入新的root密码时,输入你想要的密码…...

短视频矩阵系统:智能批量剪辑、账号管理新纪元!
在当今快节奏的数字化时代,短视频已经成为人们获取信息和娱乐的主要途径。 然而,对于创作者和企业来说,如何高效地管理多个短视频账号并保持内容的质量和一致性,成为了一个令人头疼的问题。 短视频矩阵系统就是为了解决这一难题…...

【SpringMVC - 1】基本介绍+快速入门+图文解析SpringMVC执行流程
目录 1.Spring MVC的基本介绍 2.大致分析SpringMVC工作流程 3.SpringMVC的快速入门 首先大家先自行配置一个Tomcat 文件的配置 配置 WEB-INF/web.xml 创建web/login.jsp 创建com.ygd.web.UserServlet控制类 创建src下的applicationContext.xml文件 重点的注意事项和说明…...

vitepress博客模板搭建
vitepress博客搭建 个人博客技术栈更新,快速搭建一个vitepress自定义博客 建议去博客查看文章,观感更佳。原文地址 模板仓库: vitepress-blog-template 前言 服务器过期快一年了,博客也快一年没更新了,最近重新搭…...

Git入门图文教程 -- 深入浅出 ( 保姆级 )
01、认识一下Git!—简介 Git是当前最先进、最主流的分布式版本控制系统,免费、开源!核心能力就是版本控制。再具体一点,就是面向代码文件的版本控制,代码的任何修改历史都会被记录管理起来,意味着可以恢复…...
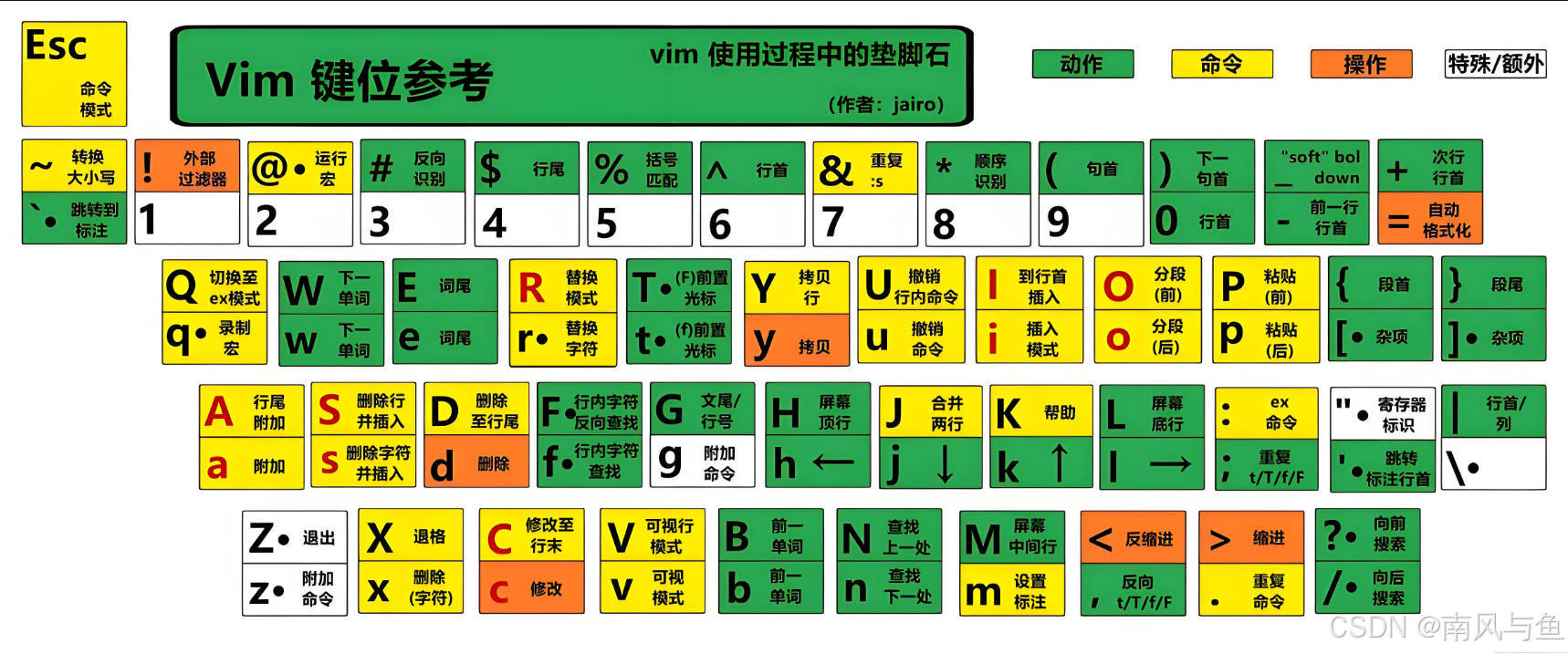
Linux编辑器 - vim
目录 一、vim 的基本概念 1. 正常/普通/命令模式(Normal mode) 2. 插入模式(Insert mode) 3. 末行模式(last line mode) 二、vim 的基本操作 三、vim 正常模式命令集 1. 插入模式 2. 移动光标 3. 删除文字 4. 复制 5. 替换 6. 撤销上一次操作 7. 更改 8. 调至指定…...

Spring Security使用基本认证(Basic Auth)保护REST API
基本认证概述 基本认证(Basic Auth)是保护REST API最简单的方式之一。它通过在HTTP请求头中携带Base64编码过的用户名和密码来进行身份验证。由于基本认证不使用cookie,因此没有会话或用户登出的概念,这意味着每次请求都必须包含…...

MySQL —— explain 查看执行计划与 MySQL 优化
文章目录 explain 查看执行计划explain 的作用——查看执行计划explain 查看执行计划返回信息详解表的读取顺序(id)查询类型(select_type)数据库表名(table)联接类型(type)可用的索引…...

出海第一步:搞定业务系统的多区域部署
出海的企业越来越多,他们不约而同开始在全球范围内部署应用程序。这样做的原因有很多,例如降低延迟,改善用户体验;满足一些国家或地区的数据隐私法规与合规要求;通过在全球范围内部署应用程序来提高容灾能力和可用性&a…...

二手手机回收小程序,一键便捷高效回收
随着科技的不断升级,智能手机也在快速进行更新换代,出现了大量的闲置手机,这为二手手机市场提供了巨大的发展空间! 经过手机回收市场的快速发展,二手手机回收已经成为了消费者的新选择,既能够减少手机的浪…...
)
开源模型应用落地-Qwen2.5-7B-Instruct与vllm实现离线推理-性能分析(四)
一、前言 离线推理能够在模型训练完成后,特别是在处理大规模数据时,利用预先准备好的输入数据进行批量推理,从而显著提高计算效率和响应速度。通过离线推理,可以在不依赖实时计算的情况下,快速生成预测结果,从而优化决策流程和提升用户体验。此外,离线推理还可以降低云计…...

深入解析小程序组件:view 和 scroll-view 的基本用法
深入解析小程序组件:view 和 scroll-view 的基本用法 引言 在微信小程序的开发中,组件是构建用户界面的基本单元。两个常用的组件是 view 和 scroll-view。这两个组件不仅功能强大,而且使用灵活,是开发者实现复杂布局和交互的基础。本文将深入探讨这两个组件的基本用法,…...

【汇编语言】转移指令的原理(三) —— 汇编跳转指南:jcxz、loop与位移的深度解读
文章目录 前言1. jcxz 指令1.1 什么是jcxz指令1.2 如何操作 2. loop 指令2.1 什么是loop指令2.2 如何操作 3. 根据位移进行转移的意义3.1 为什么?3.2 举例说明 4. 编译器对转移位移超界的检测结语 前言 📌 汇编语言是很多相关课程(如数据结构…...

opencv-python 分离边缘粘连的物体(距离变换)
import cv2 import numpy as np# 读取图像,这里添加了判断图像是否读取成功的逻辑 img cv2.imread("./640.png") # 灰度图 gray cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 高斯模糊 gray cv2.GaussianBlur(gray, (5, 5), 0) # 二值化 ret, binary cv2…...

机器学习杂笔记1:类型-数据集-效果评估-sklearn-机器学习算法分类
文章目录 1.类型2.数据集3.效果评估4.sklearn5.sklearn机器学习算法七种数据分析方法1.对比分析2.细分分析3.A/B测试 (单一变量分析)4.漏斗分析5.留存分析6.相关分析7.聚类分析 1.类型 【1】监督学习:从成对的已经标记好的输入和输出经验数据…...

Django+Nginx+uwsgi网站使用Channels+redis+daphne实现简单的多人在线聊天及消息存储功能
网站部署在华为云服务器上,Debian系统,使用DjangoNginxuwsgi搭建。最终效果如下图所示。 一、响应逻辑顺序 1. 聊天页面请求 客户端请求/chat/(输入聊天室房间号界面)和/chat/room_name(某个聊天室页面)链…...

数据结构在二叉树Oj中利用子问题思路来解决问题
二叉树Oj题 获取二叉树的节点数获取二叉树的终端节点个数获取k层节点的个数获取二叉树的高度检测为value的元素是否存在判断两颗树是否相同判断是否是另一棵的子树反转二叉树判断一颗二叉树是否是平衡二叉树时间复杂度O(n*n)复杂度O(N) 二叉树的遍历判断是否是对称的二叉树二叉…...

华为openEuler考试真题演练(附答案)
【单选题】 以下关于互联网的描述,哪个选项是正确的? A:Nginx 在万维网中可以作为 ftp 服务器的反向代理,并与ftp服务器的数量--对应 B:Nginx 在互联网中可以作为 web服务器端,成为万维网的一个节点 C:互联网上的的资源需使用 Nginx进行七层…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
