集合卡尔曼滤波(Ensemble Kalman Filter),用于二维滤波(模拟平面上的目标跟踪),MATLAB代码

集合卡尔曼滤波(Ensemble Kalman Filter)
文章目录
- 引言
- 理论基础
- 卡尔曼滤波
- 集合卡尔曼滤波
- 初始化
- 预测步骤
- 更新步骤
- 卡尔曼增益
- 更新集合
- MATLAB 实现
- 运行结果
- 3. 应用领域
- 结论
引言
集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)是一种基于状态估计的非线性滤波方法,广泛应用于动态系统中的状态估计和数据同化问题。它通过使用一组样本(即“集合”)来近似状态的概率分布,有效地处理高维和非线性系统。
理论基础
卡尔曼滤波
卡尔曼滤波是一种递归算法,用于估计线性动态系统的状态。其基本模型可以描述为:
-
状态方程:
x k = A x k − 1 + B u k + w k x_k = Ax_{k-1} + Bu_k + w_k xk=Axk−1+Buk+wk
其中, x k x_k xk 是当前状态, A A A 是状态转移矩阵, B B B 是控制输入矩阵, u k u_k uk 是控制输入, w k w_k wk 是过程噪声,通常假设为高斯分布。 -
测量方程:
z k = H x k + v k z_k = Hx_k + v_k zk=Hxk+vk
其中, z k z_k zk 是测量值, H H H 是测量矩阵, v k v_k vk 是测量噪声,通常也假设为高斯分布。
集合卡尔曼滤波
当系统是非线性时,传统卡尔曼滤波的假设可能不再成立,因此需要引入集合卡尔曼滤波。EnKF的基本思想是使用一组状态样本来表示状态分布。具体步骤如下:
初始化
生成初始状态的集合:
X 0 = { x 0 1 , x 0 2 , … , x 0 N } X_0 = \{x_0^1, x_0^2, \ldots, x_0^{N}\} X0={x01,x02,…,x0N}
其中, N N N 是集合的大小。通常,样本是从初始状态的概率分布中采样。
预测步骤
根据状态方程更新每个样本:
x k i = A x k − 1 i + B u k + w k i ( i = 1 , 2 , … , N ) x_k^i = A x_{k-1}^i + B u_k + w_k^i \quad (i = 1, 2, \ldots, N) xki=Axk−1i+Buk+wki(i=1,2,…,N)
其中, w k i w_k^i wki 是从过程噪声分布中采样的噪声。
更新步骤
计算样本的均值和协方差:
-
均值:
x ˉ k = 1 N ∑ i = 1 N x k i \bar{x}_k = \frac{1}{N} \sum_{i=1}^{N} x_k^i xˉk=N1i=1∑Nxki -
协方差:
P k = 1 N − 1 ∑ i = 1 N ( x k i − x ˉ k ) ( x k i − x ˉ k ) T P_k = \frac{1}{N-1} \sum_{i=1}^{N} (x_k^i - \bar{x}_k)(x_k^i - \bar{x}_k)^T Pk=N−11i=1∑N(xki−xˉk)(xki−xˉk)T
根据测量方程计算创新和创新协方差:
-
创新:
y k = z k − H x ˉ k y_k = z_k - H \bar{x}_k yk=zk−Hxˉk -
创新协方差:
S k = H P k H T + R S_k = H P_k H^T + R Sk=HPkHT+R
其中, R R R 是测量噪声的协方差。
卡尔曼增益
计算卡尔曼增益:
K k = P k H T S k − 1 K_k = P_k H^T S_k^{-1} Kk=PkHTSk−1
更新集合
最后,更新每个样本:
x k i = x k i + K k y k ( i = 1 , 2 , … , N ) x_k^i = x_k^i + K_k y_k \quad (i = 1, 2, \ldots, N) xki=xki+Kkyk(i=1,2,…,N)
MATLAB 实现
以下是基于上述理论的 MATLAB 代码示例,用于实现集合卡尔曼滤波:
% 集合卡尔曼滤波示例
% 2024-11-12/Ver1
clear; clc; close all; % 清除工作空间,清空命令窗口,关闭所有图形窗口
rng(0); % 设置随机数生成器的种子,以确保结果可重复% 参数设置
n = 4; % 状态维度(4个状态变量)
m = 2; % 测量维度(2个测量变量)
N = 100; % 时间步数(总共进行100个时间步的模拟)
num_ensemble = 10; % 集合成员数量(使用10个样本进行估计)
process_noise_cov = 1e-5 * eye(n); % 过程噪声协方差矩阵(小值,表示低噪声)
measurement_noise_cov = 1 * eye(m); % 测量噪声协方差矩阵(较大值,表示较高噪声)% 初始化真实状态
true_state = zeros(n, N); % 创建一个n行N列的零矩阵,用于存储真实状态
true_state(:, 1) = [1; 0; 2; 1]; % 设置初始真实状态(X位移、X速度、Y位移、Y速度)T = 1; %时间间隔
% 状态转移矩阵
A = [1 T 0 0; % 状态转移矩阵,定义如何从一个状态转移到下一个状态0 1 0 0; 0 0 1 T; 0 0 0 1];% 测量矩阵
H = [1 0 0 0; % 测量矩阵,定义如何从状态生成测量值0 0 1 0];
完整代码下载链接:https://download.csdn.net/download/callmeup/89986951
运行结果
轨迹图:

状态曲线:

误差曲线:

误差统计特性输出:

3. 应用领域
集合卡尔曼滤波在多个领域中得到了广泛应用,包括:
- 气象学:在天气预报和气候模型中进行数据同化。
- 环境科学:用于水文模型、污染扩散模型等。
- 机器人:在定位和导航中进行状态估计。
- 金融:用于时间序列数据的预测与分析。
结论
集合卡尔曼滤波是一种强大的工具,能够在复杂的非线性和高维状态空间中实现有效的状态估计。通过使用集合样本来近似状态分布,EnKF克服了传统卡尔曼滤波在处理非线性问题时的局限性,具有良好的计算效率和灵活性。随着数据同化和状态估计需求的增加,EnKF的应用前景将更加广泛。
如有需要,可私信或通过下方的卡片联系我
相关文章:

集合卡尔曼滤波(Ensemble Kalman Filter),用于二维滤波(模拟平面上的目标跟踪),MATLAB代码
集合卡尔曼滤波(Ensemble Kalman Filter) 文章目录 引言理论基础卡尔曼滤波集合卡尔曼滤波初始化预测步骤更新步骤卡尔曼增益更新集合 MATLAB 实现运行结果3. 应用领域结论 引言 集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)是…...

北京申请中级职称流程(2024年)
想找个完整详细点的申请流程资料真不容易,做个分享送给需要的人吧。 不清楚为什么说文章过度宣传,把链接和页面去掉了,网上自己找一下。 最好用windows自带的EDGE浏览器打开申请网站,只有在开始申请的时间内才可以进行网上申报&…...

ubuntu.24安装cuda
1.下载CUDA Toolkit https://developer.nvidia.com/cuda-toolkit-archive 2.按照命令下载,安装 sudo sh cuda_12.2.2_535.104.05_linux.run 3.环境变量 sudo vi /etc/profile 最后面添加 export PATH“/usr/local/cuda-12.2/bin: P A T H " e x p o r t L D L…...

unity li2cpp逆向原理是什么?
主要涉及将Unity游戏引擎中的C#代码转换为C代码,并进一步编译为各平台的原生(Native)代码的过程,以及逆向工程工具如何利用这一过程中的特定文件来还原和分析原始代码。以下是对Unity IL2CPP逆向原理的详细解释: 对惹…...

Python网络爬虫实践案例:爬取猫眼电影Top100
以下是一个Python网络爬虫的实践案例,该案例将演示如何使用Python爬取猫眼电影Top100的电影名称、主演和上映时间等信息,并将这些信息保存到TXT文件中。此案例使用了requests库来发送HTTP请求,使用re库进行正则表达式匹配,并包含详…...

卷积神经网络(CNN)中的权重(weights)和偏置项(bias)
在卷积神经网络(CNN)中,权重(weights)和偏置项(bias)是两个至关重要的参数,它们在网络的学习和推断过程中起着关键作用。 一、权重(Weights) 1. 定义…...

华为FusionCube 500-8.2.0SPC100 实施部署文档
环境: 产品:FusionCube 500版本:8.2.0.SPC100场景:虚拟化基础设施平台:FusionCompute两节点 MCNA * 2硬件部署(塔式交付场景)免交换组网(配置AR卡) 前置准备 组网规划 节…...
OKHttp网络通信)
Android 网络请求(二)OKHttp网络通信
学习笔记 OkHttp 是一个非常强大且流行的 HTTP 客户端库,广泛用于 Android 开发中进行网络请求。与 HttpURLConnection 相比,OkHttp 提供了更简单、更高效的 API,特别是在处理复杂的 HTTP 请求时。 如何使用 OkHttp 进行网络请求 以下是使…...

npm上传自己封装的插件(vue+vite)
一、npm账号及发包删包等命令 若没有账号,可在npm官网:https://www.npmjs.com/login 进行注册。 在当前项目根目录下打开终端命令窗口,常见命令如下: 1、登录命令:npm login(不用每次都重新登录࿰…...
如何在Word文件中设置水印以及如何禁止修改水印
在日常办公和学习中,我们经常需要在Word文档中设置水印,以保护文件的版权或标明文件的机密性。水印可以是文字形式,也可以是图片形式,能够灵活地适应不同的需求。但仅仅设置水印是不够的,有时我们还需要确保水印不被随…...

.NET桌面应用架构Demo与实战|WPF+MVVM+EFCore+IOC+DI+Code First+AutoMapper
目录 .NET桌面应用架构Demo与实战|WPFMVVMEFCoreIOCDICode FirstAutoPapper技术栈简述项目地址:功能展示项目结构项目引用1. 新建模型2. Data层,依赖EF Core,实现数据库增删改查3. Bussiness层,实现具体的业务逻辑4. Service层&am…...

el-table根据指定字段合并行和列+根据屏幕高度实时设置el-table的高度
文章目录 html代码script代码arraySpanMethod.js代码 html代码 <template><div class"rightBar"><cl-table ref"tableData"border :span-method"arraySpanMethod" :data"tableData" :columns"columns":max-…...
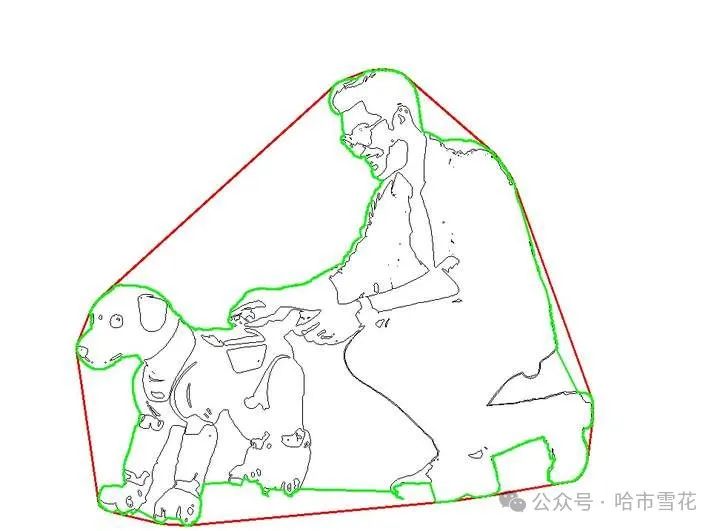
图像处理 之 凸包和最小外围轮廓生成
“ 最小包围轮廓之美” 一起来欣赏图形之美~ 1.原始图片 男人牵着机器狗 2.轮廓提取 轮廓提取 3.最小包围轮廓 最小包围轮廓 4.凸包 凸包 5.凸包和最小包围轮廓的合照 凸包和最小包围轮廓的合照 上述图片中凸包、最小外围轮廓效果为作者实现算法生成。 图形几何之美系列&#…...

萤石设备视频接入平台EasyCVR私有化视频平台视频监控系统的需求及不同场景摄像机的选择
在现代社会,随着安全意识的提高和技术的进步,安防监控视频系统已成为保障人们生活和财产安全的重要工具。EasyCVR安防监控视频系统,以其先进的网络传输技术和强大的功能,为各种规模的项目提供了一个高效、可靠的监控解决方案。以下…...

网络安全之接入控制
身份鉴别 定义:验证主题真实身份与其所声称的身份是否符合的过程,主体可以是用户、进程、主机。同时也可实现防重放,防假冒。 分类:单向鉴别、双向鉴别、三向鉴别。 主题身份标识信息:密钥、用户名和口令、证书和私钥 Internet接入控制过程 …...

Sqlite: Java使用、sqlite-devel
这里写目录标题 一、简介二、使用1. Java项目中(1)引入驱动(2)工具类(3)调用举例 2. sqlite-devel in linuxsqlite-devel使用 三、更多应用1. 数据类型2. 如何存储日期和时间3. 备份 一、简介 非常轻量级&…...

京东面试题目分享
话不多说,直接上问题 一面(视频面) 1小时30分钟 1、类加载机制概念、加载步骤、双亲委托机制、全盘委托机制、类加载器种类及继承关系 2、如何实现让类加载器去加载网络上的资源文件?怎么自定义类加载器?自定义的加…...

STM32 使用 STM32CubeMX HAL库实现低功耗模式
STM32 使用 HAL 库的低功耗模式测试使用 ...... 矜辰所致前言 上次画了一个 STM32L010F4 最小系统的板子,也做了一些基本测试,但是最重要的低功耗一直拖到现在,以前在使用 STM32L151 的时候用标准库做过低功耗的项目,现在都使…...
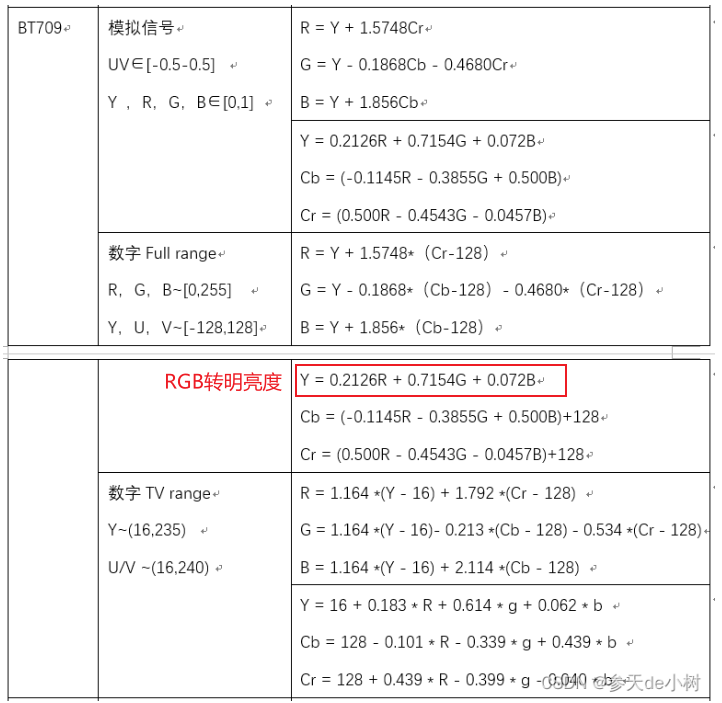
技术美术百人计划 | 《2.1 色彩空间介绍》笔记
总览 一、色彩发送器 色彩认知: 光源是出生点,光源发射出光线,光线通过直射反射折射等路径最终进入人眼。 但人眼接收到光线后,人眼的细胞产生了一系列化学反应。 由此把产生的信号传入大脑,最终大脑对颜色产生了认…...
如何在 Ubuntu 上安装 Mosquitto MQTT 代理
如何在 Ubuntu 上安装 Mosquitto MQTT 代理 Mosquitto 是一个开源的消息代理,实现了消息队列遥测传输 (MQTT) 协议。在 Ubuntu 22.04 上安装 MQTT 代理,您可以利用 MQTT 轻量级的 TCP/IP 消息平台,该平台专为资源有限的物联网 (IoT) 设备设计…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
