java-贪心算法
1. 霍夫曼编码(Huffman Coding)
描述:
霍夫曼编码是一种使用变长编码表对数据进行编码的算法,由David A. Huffman在1952年发明。它是一种贪心算法,用于数据压缩。霍夫曼编码通过构建一个二叉树(霍夫曼树),树中的每个叶子节点代表一个字符,树的权重表示字符出现的频率。构建树的过程中,总是将两个权重最小的节点合并。
Java案例:
import java.util.PriorityQueue;public class HuffmanCoding {static class Node {char data;int frequency;Node left, right;Node(char data, int frequency) {this.data = data;this.frequency = frequency;left = right = null;}}// 构建霍夫曼树static Node buildHuffmanTree(char data[], int frequency[]) {PriorityQueue<Node> minHeap = new PriorityQueue<>((a, b) -> a.frequency - b.frequency);for (int i = 0; i < data.length; i++) {minHeap.add(new Node(data[i], frequency[i]));}while (minHeap.size() > 1) {Node x = minHeap.poll();Node y = minHeap.poll();Node f = new Node('\0', x.frequency + y.frequency);f.left = x;f.right = y;minHeap.add(f);}return minHeap.poll();}// 打印霍夫曼编码static void printCodes(Node root, String s) {if (root.left == null && root.right == null && Character.isLetter(root.data)) {System.out.println(root.data + ": " + s);return;}printCodes(root.left, s + "0");printCodes(root.right, s + "1");}public static void main(String[] args) {char data[] = {'a', 'b', 'c', 'd', 'e', 'f'};int frequency[] = {5, 9, 12, 13, 16, 45};Node root = buildHuffmanTree(data, frequency);printCodes(root, "");}
}
2. 活动选择问题(Activity Selection Problem)
描述:
活动选择问题是一个经典的贪心算法问题,给定一系列活动,每个活动都有开始时间和结束时间,目标是选择最大数量的互不重叠的活动。
Java案例:
import java.util.Arrays;public class ActivitySelection {public static void selectActivities(int start[], int end[]) {Arrays.sort(end); // 按结束时间排序int i = 0, activities = 0;for (int j = 1; j < end.length; j++) {if (start[i] < end[j]) { // 如果当前活动的开始时间小于前一个活动的结束时间activities++;i = j; // 更新当前活动的索引}}System.out.println("Total activities selected: " + activities);}public static void main(String[] args) {int start[] = {1, 3, 0, 5, 8, 5};int end[] = {2, 4, 6, 7, 9, 9};selectActivities(start, end);}
}
3. 硬币找零问题(Coin Change Problem)
描述:
硬币找零问题是一个典型的贪心算法问题,给定不同面额的硬币和一个总金额,目标是使用最少数量的硬币凑成总金额。
Java案例:
public class CoinChange {public static int coinChange(int[] coins, int amount) {int[] dp = new int[amount + 1];Arrays.fill(dp, amount + 1); // 初始化为最大值dp[0] = 0; // 0元需要0个硬币for (int i = 1; i <= amount; i++) {for (int coin : coins) {if (i >= coin && dp[i - coin] != amount + 1) {dp[i] = Math.min(dp[i], dp[i - coin] + 1);}}}return dp[amount] > amount ? -1 : dp[amount];}public static void main(String[] args) {int[] coins = {1, 2, 5};int amount = 11;int result = coinChange(coins, amount);if (result != -1) {System.out.println("Minimum number of coins required: " + result);} else {System.out.println("Not possible to make the given amount");}}
}
这些案例展示了贪心算法在不同问题中的应用,包括霍夫曼编码、活动选择问题和硬币找零问题。贪心算法通过在每一步选择局部最优解来寻找全局最优解。
🌐 霍夫曼编码和哈夫曼编码有什么区别?
霍夫曼编码(Huffman Coding)和哈夫曼编码(Huffman Coding)实际上是同一个概念,只是翻译名称上的不同。在中文文献和技术社区中,这两种叫法都被广泛使用,但它们指的是同一种编码方法。
霍夫曼编码是一种广泛使用的无损数据压缩算法,由David A. Huffman在1952年发明。它是一种贪心算法,通过构建一个二叉树(霍夫曼树)来为输入字符分配可变长度的编码。树的叶子节点代表输入字符,而树的权重表示字符出现的频率。构建树的过程中,总是将两个权重最小的节点合并,直到构建出完整的霍夫曼树。然后,通过遍历树来为每个字符分配一个唯一的二进制编码,频率高的字符会被分配较短的编码,而频率低的字符则会被分配较长的编码。
因此,当你看到“霍夫曼编码”和“哈夫曼编码”时,可以认为它们是同一个算法的不同叫法。在英文中,这个算法统一被称为“Huffman Coding”。

🤔 霍夫曼编码在哪些场景下应用效果最好?
霍夫曼编码(Huffman Coding)在以下场景下应用效果最好:
-
文件压缩:
霍夫曼编码广泛应用于文件压缩领域,特别是在存储文件时,可以通过压缩来节省磁盘空间。虽然文件压缩后需要解压缩才能使用,但这通常是一次性的操作,因此空间和时间的权衡是可接受的。例如,在文件系统中存储不常使用的文件时,使用霍夫曼编码进行压缩可以显著减少存储空间的需求。 -
数据通信:
在数据通信领域,霍夫曼编码可以减少通信和I/O开销,特别是在高速流处理中。压缩原始模拟数据并在后处理前解压缩可以显著提高工作效率。 -
图像和视频压缩:
霍夫曼编码是许多图像和视频压缩标准的一部分,如JPEG。它用于对图像和视频数据进行无损压缩,是这些应用中不可或缺的一部分。 -
大规模科学数据集:
霍夫曼编码也被广泛用于压缩大型科学数据集,这些数据集对数据保真度有很高的要求。它在这些应用中表现出色,因为它可以有效地压缩数据,同时保持高数据保真度。 -
文本编码:
霍夫曼编码用于文本编码,特别是在不同字符使用频率差异较大的情况下。它通过为更频繁出现的字符分配较短的编码来实现空间效率,这在英语文档等文本中尤其有效,因为不同字母的使用频率差异很大。 -
通用无损压缩软件或库:
霍夫曼编码是许多通用无损压缩软件或库(如GZIP、Zstd和Blosc)中的关键步骤,它提供了一种有效的熵编码算法。 -
错误有界损失压缩:
在一些需要错误有界损失压缩的应用中,霍夫曼编码也被广泛使用,例如SZ和MGARD压缩器,这些压缩器在压缩大数据集时非常有效。
综上所述,霍夫曼编码在需要有效压缩数据以节省空间或减少传输时间的场景中效果最好,尤其是在字符使用频率不均的文本数据、图像和视频数据以及大规模科学数据集的压缩中。
📈 霍夫曼编码在减少网络带宽方面有哪些优势?
霍夫曼编码在减少网络带宽方面的优势主要体现在以下几个方面:
-
高效压缩:
霍夫曼编码为每个字符分配一个基于其出现频率的变长编码,高频字符使用较短的编码,低频字符使用较长的编码。这种优化可以显著减少数据的整体大小,从而减少网络传输所需的带宽。 -
适应性:
霍夫曼编码是自适应的,可以根据数据的实际内容动态构建最优编码树。这意味着它能够针对特定的数据集进行优化,与固定编码方案相比,能够更有效地压缩数据。 -
无损压缩:
霍夫曼编码是一种无损压缩算法,这意味着压缩和解压后的数据与原始数据完全相同。这对于必须确保数据完整性的应用场景(如文件传输、视频流等)至关重要。 -
广泛支持:
霍夫曼编码被广泛支持和实现在各种压缩工具和协议中,如HTTP压缩、ZIP文件格式、JPEG图像压缩等。这种广泛的支持意味着它可以很容易地集成到现有的网络通信系统中。 -
减少延迟:
通过减少数据的大小,霍夫曼编码可以减少数据在网络上的传输时间,从而降低延迟,特别是在高延迟网络环境中。 -
节省成本:
减少网络带宽的使用可以直接降低网络服务提供商的成本,尤其是在需要支付流量费用的场景下,如移动数据服务。 -
提高吞吐量:
在带宽受限的网络中,更有效地压缩数据可以提高网络的吞吐量,允许在同一带宽内传输更多的数据。 -
支持流式传输:
霍夫曼编码支持流式压缩和解压,这意味着数据可以边传输边解压,而不需要等待整个文件传输完成,这对于流媒体应用(如视频会议和在线视频流)非常有用。 -
易于实现:
霍夫曼编码算法相对简单,易于实现,并且有许多现成的库和工具可供使用,这使得它能够快速部署在各种网络应用中。 -
可扩展性:
霍夫曼编码可以应用于不同规模的数据,从小型文本文件到大型视频文件,都能有效地减少所需的网络带宽。
综上所述,霍夫曼编码在减少网络带宽方面的优势使其成为网络数据传输中不可或缺的技术之一。
相关文章:

java-贪心算法
1. 霍夫曼编码(Huffman Coding) 描述: 霍夫曼编码是一种使用变长编码表对数据进行编码的算法,由David A. Huffman在1952年发明。它是一种贪心算法,用于数据压缩。霍夫曼编码通过构建一个二叉树(霍夫曼树&a…...

OpenCV和Qt坐标系不一致问题
“ OpenCV和QT坐标系导致绘图精度下降问题。” OpenCV和Qt常用的坐标系都是笛卡尔坐标系,但是细微处有些不同。 01 — OpenCV坐标系 OpenCV是图像处理库,是以图像像素为一个坐标位置,即一个像素对应一个坐标,所以其坐标系也叫图像…...

前端VUE项目启动方式
将VUE项目的前端项目运行起来,整个过程非常简单,预计5分钟就可以完成,取决于大家的网速。 项目运行先安装Node.js Windows 安装 Node.js 指南:http://www.iocoder.cn/NodeJS/windows-install(opens new window) Mac 安装 Node.js…...
)
Python小白学习教程从入门到入坑------习题课5(基础巩固)
目录 实战题 1、“千年虫”是什么虫? 2、模拟京东购物流程 3、模拟12306火车票订票流程 4、模拟手机通讯录 实战题 1、“千年虫”是什么虫? 要求:已知一个列表中存储的是员工的出生年份 [88,89,90,98,00,99] 由于时间比较久,出生的年份均为2位整数…...

飞凌嵌入式T113-i开发板RISC-V核的实时应用方案
随着市场对嵌入式设备的功能需求越来越高,集成了嵌入式处理器和实时处理器的主控方案日益增多,以便更好地平衡性能与效率——实时核负责高实时性任务,A核处理复杂任务,两核间需实时交换数据。然而在数据传输方面,传统串…...

基于Java后台实现百度、高德和WGS84坐标的转换实战
目录 前言 一、需求的缘由 1、百度坐标拾取 2、高德坐标拾取 3、不同地图的坐标展示 二、后端坐标偏移转换处理 1、相关类库介绍 2、coordtransorm类图介绍 3、后台实际转换 三、总结 前言 在当今数字化时代,地理位置信息的精确性和实时性对于各种应用至…...

SQL,力扣题目1635,Hopper 公司查询 I
一、力扣链接 LeetCode_1635 二、题目描述 表: Drivers ---------------------- | Column Name | Type | ---------------------- | driver_id | int | | join_date | date | ---------------------- driver_id 是该表的主键(具有唯一值的列)。 该表的每一行…...

Android 分区相关介绍
目录 一、MTK平台 1、MTK平台分区表配置 2、MTK平台刷机配置表 3、MTK平台分区表配置不生效 4、Super分区的研究 1)Super partition layout 2)Block device table 二、高通平台 三、展锐平台 四、相关案例 1、Super分区不够导致编译报错 经验…...

JMeter监听器与压测监控之 InfluxDB
1. 简介 在本文中,我们将介绍如何在 Kali Linux 上通过 Docker 安装 InfluxDB,并使用 JMeter 对其进行性能监控。InfluxDB 是一个高性能的时序数据库,而 JMeter 是一个开源的性能测试工具,可以用于对各种服务进行负载测试和性能监…...

信息安全管理与评估赛项(网络安全)--应急响应专项训练
web1 题目来源:https://mp.weixin.qq.com/s/89IS3jPePjBHFKPXnGmKfA 题目 1.攻击者的shell密码2.攻击者的IP地址3.攻击者的隐藏账户名称4.攻击者挖矿程序的矿池域名(仅域名)5.有实力的可以尝试着修复漏洞靶机 用户:administrator密码:Zgsfadmin.com题解 攻击者…...
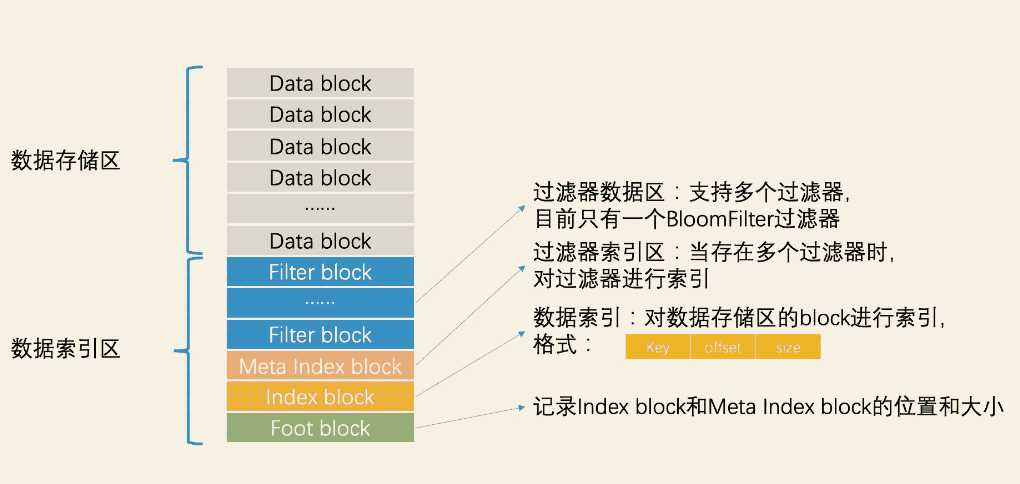
ElasticSearch学习篇18_《检索技术核心20讲》LevelDB设计思想
目录 一些常见的设计思想以及基于LSM树的LevelDB是如何利用这些设计思想优化存储、检索效率的。 几种常见的设计思想 索引和数据分离减少磁盘IO读写分离分层思想 LevelDB的设计思想 读写分离设计分层设计与延迟合并LRU缓存加速检索 几种常见设计思想 索引与数据分离 索引…...

使用 FFmpeg 提取音频的详细指南
FFmpeg 是一个开源的多媒体处理工具,支持视频、音频的编码、解码、转换等多种功能。通过 FFmpeg,提取视频中的音频并保存为各种格式非常简单和高效。这在音视频剪辑、媒体处理、转码等场景中具有广泛的应用。 本文将详细讲解如何使用 FFmpeg 提取音频&a…...

中国省级新质生产力发展指数数据(任宇新版本)2010-2023年
一、测算方式:参考C刊《财经理论与实践》任宇新(2024)老师的研究,新质生产力以劳动者劳动资料劳动对象及其优化组合的质变为 基本内涵,借 鉴 王 珏 和 王 荣 基 的 做 法构建新质生产力发展水平评价指标体系如下所示&a…...
 房屋建造案例)
C++设计模式:建造者模式(Builder) 房屋建造案例
什么是建造者模式? 建造者模式是一种创建型设计模式,它用于一步步地构建一个复杂对象,同时将对象的构建过程与它的表示分离开。简单来说: 它将复杂对象的“建造步骤”分成多部分,让我们可以灵活地控制这些步骤。通过…...

Python 快速入门(上篇)❖ Python基础知识
Python 基础知识 Python安装**运行第一个程序:基本数据类型算术运算符变量赋值操作符转义符获取用户输入综合案例:简单计算器实现Python安装** Linux安装: yum install python36 -y或者编译安装指定版本:https://www.python.org/downloads/source/ wget https://www.pyt…...

string接口的模拟实现
文章目录 一. string底层逻辑演示声明和定义分开 二. size()三. operator[]四. 迭代器四. const迭代器五. 预留空间(reserve)六. 尾插一个字符push_back七. 尾插一个字符串append八. operator九. operator 一. string底层逻辑 (1)为了和库里面…...

sed使用扩展正则表达式时, -i 要写在 -r 或 -E 的后面
sed使用扩展正则表达式时, -i 要写在 -r 或 -E 的后面 前言 -r 等效 -E , 启用扩展正则表达式 -E是新叫法,更统一,能增强可移植性 , 但老系统,比如 CentOS-7 的 sed 只能用 -r ### Ubuntu24.04-E, -r, --regexp-extendeduse extended regular expressions in the script(fo…...

Verilog HDL可综合与不可综合语句
目录 什么是逻辑综合 可综合语句 不可综合语句 逻辑综合建模建议 综合流程 什么是逻辑综合 所谓逻辑综合就是在标准单元库和特定的设计约束的基础上,把设计的高层次描述转换成优化的门级网表的过程。 标准单元库(工艺库)可以包含简单的…...
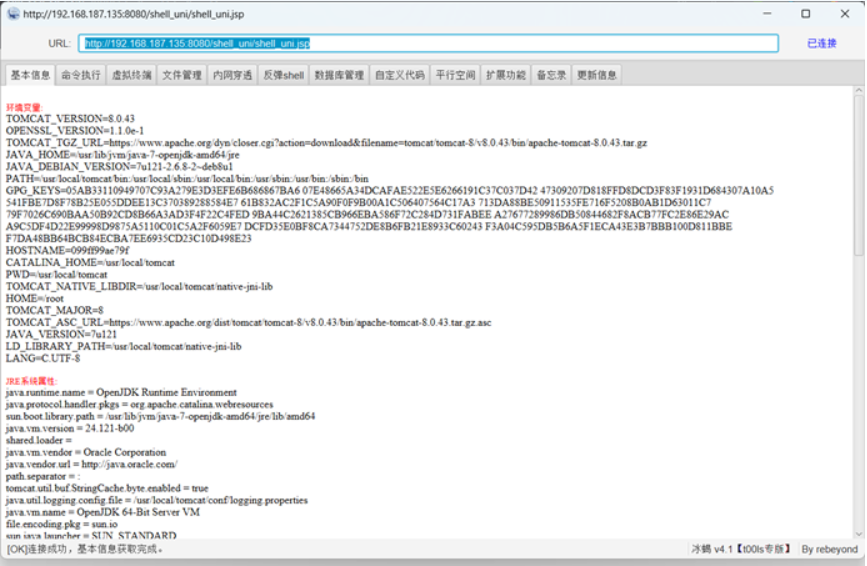
tomcat 后台部署 war 包 getshell
1. tomcat 后台部署 war 包 getshell 首先进入该漏洞的文件目录 使用docker启动靶场环境 查看端口的开放情况 访问靶场:192.168.187.135:8080 访问靶机地址 http://192.168.187.135:8080/manager/html Tomcat 默认页面登录管理就在 manager/html 下,…...

网络云计算】2024第47周-每日【2024/11/21】周考-实操题-RAID6实操解析1
文章目录 1、RAID6配置指南(大致步骤)2、注意事项3、截图和视频 网络云计算】2024第47周-每日【2024/11/21】周考-实操题-RAID6实操 RAID6是一种在存储系统中实现数据冗余和容错的技术,其最多可以容忍两块磁盘同时损坏而不造成数据丢失。RAID…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
