深入解密 K 均值聚类:从理论基础到 Python 实践
1. 引言
在机器学习领域,聚类是一种无监督学习的技术,用于将数据集分组成若干个类别,使得同组数据之间具有更高的相似性。这种技术在各个领域都有广泛的应用,比如客户细分、图像压缩和市场分析等。聚类的目标是使得同类样本之间的相似性最大化,而不同类样本之间的相似性最小化。
K 均值聚类 (K-Means Clustering) 是一种基于距离度量的迭代优化算法,通过选择若干个质心 (centroid) 来对数据进行分组,使得每个数据点所属的聚类内距离质心的距离之和最小化。由于其算法的简单性和高效性,K 均值在数据分析中被广泛使用。
在现实生活中,我们可以将 K 均值聚类应用于客户细分,以帮助企业识别具有相似购买行为的客户群体,或者用于图像压缩,通过将图像像素点聚类来减少颜色的数量。在这篇文章中,我们将深入探讨 K 均值聚类的数学原理、算法实现步骤,并提供 Python 代码示例来帮助读者理解其实际应用。
2. 什么是 K 均值聚类?
K 均值聚类是一种基于质心的聚类算法,它通过反复迭代的方式将数据点分配到 K 个聚类中。每个质心代表一个聚类的中心位置,算法会不断调整质心的位置,直到满足一定的收敛条件。K 均值聚类的目标是最小化每个聚类内部所有点到其质心的距离之和。
具体来说,K 均值聚类的步骤可以概括如下:
-
随机选择 K 个初始质心。
-
将每个数据点分配到离它最近的质心所在的聚类。
-
重新计算每个聚类的质心,即对聚类中的所有数据点取平均值。
-
重复步骤 2 和 3,直到质心的位置不再发生变化,或者达到预设的迭代次数。
K 均值聚类的最终结果是 K 个聚类,每个聚类由一个质心及其所有属于该聚类的数据点组成。其目标是使得每个聚类内的数据点与质心之间的总距离最小。
3. K 均值聚类的数学原理
K 均值聚类的目标是最小化每个数据点到所属质心的距离的平方和 (Sum of Squared Errors, SSE):

其中,
-
:聚类的数量。
-
:第 i 个聚类。
-
:第 i 个聚类的质心。
-
:属于聚类 的数据点。
这个优化问题的目标是通过不断调整每个聚类的质心来最小化 SSE。该过程通过交替进行两步:分配 (Assignment) 和更新 (Update),直到达到收敛条件。
4. 算法实现步骤详解
K 均值聚类算法主要包含以下步骤:
步骤 1:选择 K 值
K 值是指要将数据分成的聚类数。选择合适的 K 值是 K 均值聚类算法中一个非常重要的步骤,因为不合适的 K 值会影响聚类的效果。通常可以通过 "肘部法则 (Elbow Method)" 来确定合适的 K 值。
步骤 2:初始化质心
可以随机选择 K 个数据点作为初始质心,或者使用一些启发式的方法,如 K-Means++,以更好地初始化质心,减少随机性对聚类效果的影响。
步骤 3:分配数据点
将每个数据点分配到离它最近的质心所在的聚类中。通常使用欧几里得距离来计算数据点与质心之间的距离。
步骤 4:更新质心
对于每一个聚类,重新计算其质心的位置。具体来说,将聚类中的所有数据点的坐标进行平均,得到新的质心位置。
步骤 5:收敛判断
判断质心是否发生变化。如果质心位置不再变化,或者达到预设的最大迭代次数,算法停止。此时的聚类结果即为最终的聚类划分。
5. Python 代码实现
下面我们用 Python 及其常用库 NumPy 和 Matplotlib 实现 K 均值聚类算法:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# 生成模拟数据集
np.random.seed(42)
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=0)
# 可视化数据集
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Generated Data')
plt.show()
# 定义K均值聚类算法
class KMeans:def __init__(self, k=3, max_iters=100, tol=1e-4):self.k = kself.max_iters = max_itersself.tol = tol
def fit(self, X):self.centroids = X[np.random.choice(range(X.shape[0]), self.k, replace=False)]for _ in range(self.max_iters):# 分配数据点到最近的质心self.clusters = self._assign_clusters(X)# 重新计算质心new_centroids = self._compute_centroids(X)# 检查质心是否收敛if np.all(np.linalg.norm(self.centroids - new_centroids, axis=1) < self.tol):breakself.centroids = new_centroids
def _assign_clusters(self, X):distances = np.linalg.norm(X[:, np.newaxis] - self.centroids, axis=2)return np.argmin(distances, axis=1)
def _compute_centroids(self, X):return np.array([X[self.clusters == i].mean(axis=0) for i in range(self.k)])
def predict(self, X):distances = np.linalg.norm(X[:, np.newaxis] - self.centroids, axis=2)return np.argmin(distances, axis=1)
# 训练模型
kmeans = KMeans(k=4)
kmeans.fit(X)
# 预测聚类结果
y_pred = kmeans.predict(X)
# 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis', s=50)
plt.scatter(kmeans.centroids[:, 0], kmeans.centroids[:, 1], s=200, c='red', marker='X')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('K-Means Clustering Results')
plt.show()6. 选择 K 值:肘部法则
选择合适的 K 值是 K 均值聚类的重要步骤。肘部法则是一种常用的方法,它通过计算不同 K 值下 SSE 的变化趋势来选择合适的 K。随着 K 的增加,SSE 会减少,但当减少的速度显著减小时,最佳 K 值即为 "肘部点"。
以下是使用肘部法则的代码示例:
sse = []
for k in range(1, 10):kmeans = KMeans(k=k)kmeans.fit(X)sse.append(sum(np.min(np.linalg.norm(X[:, np.newaxis] - kmeans.centroids, axis=2), axis=1) ** 2))
# 可视化肘部法则
plt.plot(range(1, 10), sse, marker='o')
plt.xlabel('Number of Clusters (K)')
plt.ylabel('SSE')
plt.title('Elbow Method for Optimal K')
plt.show()7. K 均值聚类的优缺点
优点:
-
简单易懂:K 均值聚类算法简单直观,易于实现。
-
高效性:对于较大规模的数据,K 均值算法计算效率较高。
缺点:
-
对初始值敏感:算法对初始质心位置敏感,可能陷入局部最优。K-Means++ 是一种改进方法,可以更好地选择初始质心。
-
需指定 K 值:K 值需要事先给定,这对于不熟悉数据结构的用户来说是个挑战。
-
易受异常值影响:异常值对质心计算有较大影响,可能使结果偏离。
8. K-Means++ 的改进
为了减少对初始质心选择的敏感性,K-Means++ 提供了一种改进策略,确保初始质心尽可能分散,减少局部最优解的可能性。Scikit-Learn 库实现的 KMeans 就采用了 K-Means++ 作为默认的初始质心选择方法。
from sklearn.cluster import KMeans
# 使用KMeans++初始化
kmeans = KMeans(n_clusters=4, init='k-means++', max_iter=300, n_init=10, random_state=0)
y_kmeans = kmeans.fit_predict(X)
# 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, cmap='viridis', s=50)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, c='red', marker='X')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('K-Means++ Clustering Results')
plt.show()9. 实际应用
K 均值聚类在实际生活中有着广泛的应用,包括:
-
客户细分:根据购买行为或浏览习惯将客户进行分类,方便精准营销。
-
图像压缩:通过对图像的像素进行聚类,将相似颜色的像素归为同一类,从而减少颜色种类,达到压缩图像的目的。
-
市场分析:K 均值可以用于找出不同市场中的相似产品。
10. 总结
K 均值聚类是一种强大且简单的聚类算法,适合处理结构化的数值数据。它在很多应用场景下表现良好,但也有其局限性,比如对初始值敏感和易受异常值影响。在实际应用中,结合肘部法则和 K-Means++ 等改进方法,可以提高聚类效果。
希望本文让你对 K 均值聚类的原理和实现有更深的理解,并能利用代码在自己的项目中进行聚类分析。如果你有任何问题或建议,欢迎在评论区交流!
相关文章:

深入解密 K 均值聚类:从理论基础到 Python 实践
1. 引言 在机器学习领域,聚类是一种无监督学习的技术,用于将数据集分组成若干个类别,使得同组数据之间具有更高的相似性。这种技术在各个领域都有广泛的应用,比如客户细分、图像压缩和市场分析等。聚类的目标是使得同类样本之间的…...
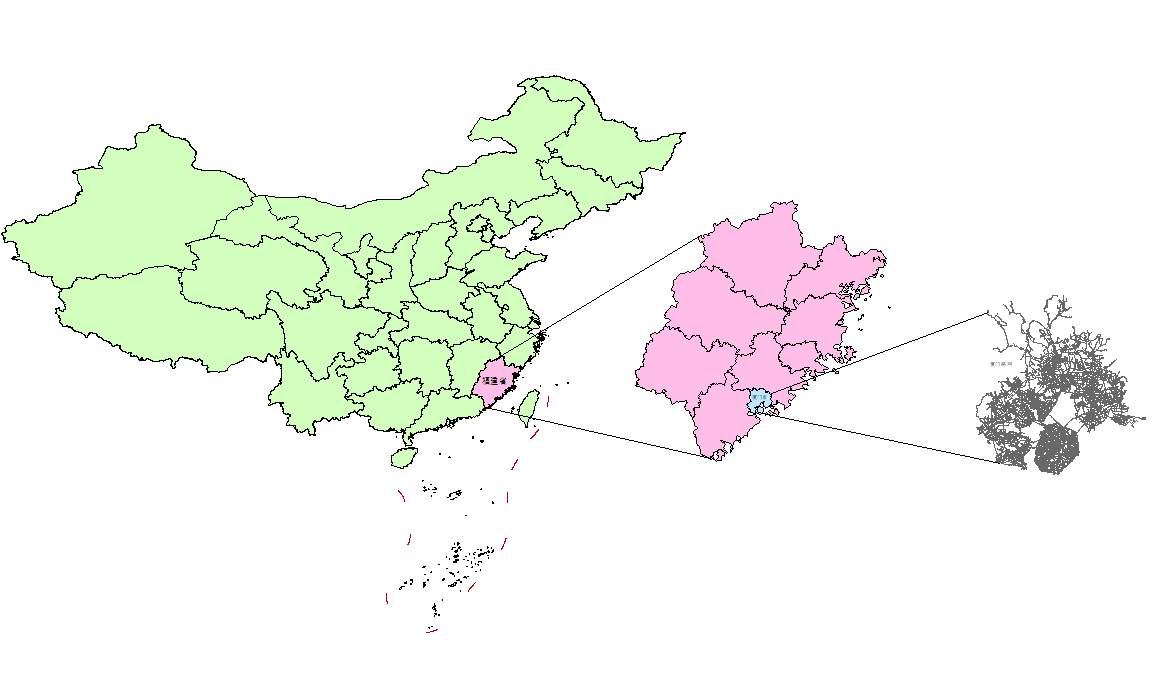
ArcGIS应用指南:ArcGIS制作局部放大地图
在地理信息系统(GIS)中,制作详细且美观的地图是一项重要的技能。地图制作不仅仅是简单地将地理数据可视化,还需要考虑地图的可读性和美观性。局部放大图是一种常见的地图设计技巧,用于展示特定区域的详细信息ÿ…...

非root用户安装CUDA
1.使用nvidia-smi查看当前驱动支持的最高CUDA版本: 表示当前驱动最多支持cuda12.1 2.进入cuda安装界面,https://developer.nvidia.com/cuda-toolkit-archive,选择想要安装的版本,例如想要安装CUDA11.4: 如果需要查看ub…...
)
单点修改,区间求和或区间询问最值(线段树)
【题目描述】 给定一个长度为n的非负整数序列,接下来有m次操作,操作共有3种:一是修改序列中某个元素的大小,二是求某个区间的所有元素的和,三是询问某个区间的最大值。整数序列下标从1开始。n<10^5, m<10^5。 …...

线性代数空间理解
学习线性代数已经很久,但是在使用过程中仍然还是不明所以,比如不知道特征向量和特征值的含义、矩阵的相乘是什么意思、如何理解矩阵的秩……。随着遇到的次数越来越多,因此我决定需要对线性代数的本质做一次深刻的探讨了。 本次主要是参考了3…...
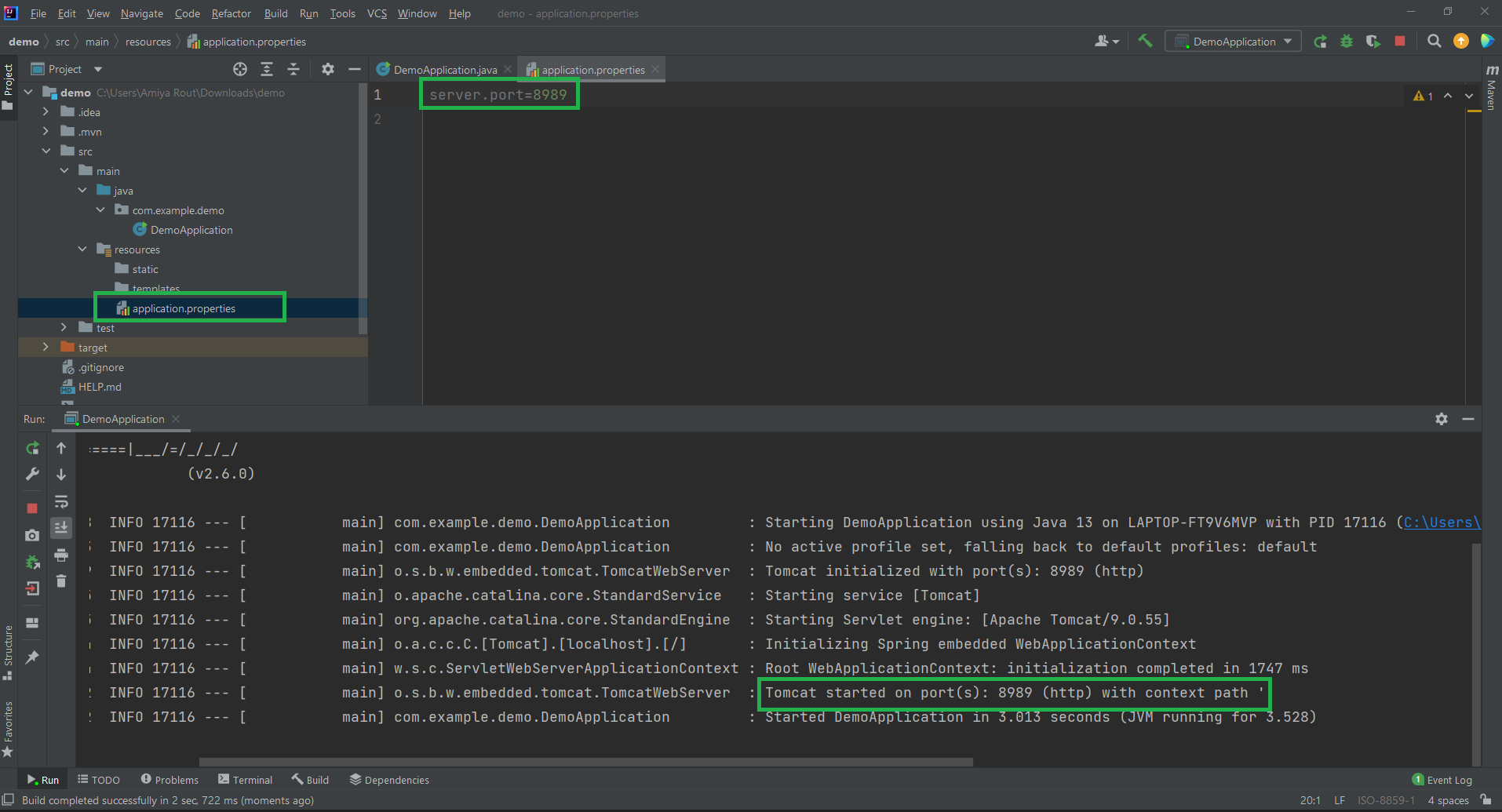
Spring Boot教程之五:在 IntelliJ IDEA 中运行第一个 Spring Boot 应用程序
在 IntelliJ IDEA 中运行第一个 Spring Boot 应用程序 IntelliJ IDEA 是一个用 Java 编写的集成开发环境 (IDE)。它用于开发计算机软件。此 IDE 由 Jetbrains 开发,提供 Apache 2 许可社区版和商业版。它是一种智能的上下文感知 IDE,可用于在各种应用程序…...

C51相关实验
C51相关实验 LED //功能:1.让开发板的LED全亮,2,点亮某一个LED,3.让LED3以5Hz的频率闪动#include "reg52.h"#define LED P2 sbit led1 LED^1;void main(void) {LED 0xff;//LED全灭led1 0;while(1)//保持应用程序不退出{} }LED 输出端是高…...

docker离线安装linux部分问题整理
0:离线安装docker过程命令 echo $PATH tar -zxvf docker-26.1.4.tgz chmod 755 -R docker cp docker/* /usr/bin/ root 权限 vim /etc/systemd/system/docker.service --------- [Unit] DescriptionDocker Application Container Engine Documentationhttps://docs.do…...

ISUP协议视频平台EasyCVR萤石设备视频接入平台银行营业网点安全防范系统解决方案
在金融行业,银行营业厅的安全保卫工作至关重要,它不仅关系到客户资金的安全,也关系到整个银行的信誉和运营效率。随着科技的发展,传统的安全防护措施已经无法满足现代银行对于高效、智能化安全管理的需求。 EasyCVR视频汇聚平台以…...

递推概念和例题
一、什么是递推 递推算法以初始值为基础,用相同的运算规律,逐次重复运算,直至求出问题的解,它的本质是按照固定的规律逐步推出(计算出)下一步的结果 这种从“起点”重复相同的的方法直至到达问题的解&…...

开发工具 - VSCode 快捷键
以下是一些常用的 VS Code 快捷键(Windows、macOS 和 Linux 均适用,略有不同): 常用快捷键 功能Windows/LinuxmacOS打开命令面板Ctrl Shift P 或 F1Cmd Shift P打开文件Ctrl OCmd O保存文件Ctrl SCmd S全部保存Ctrl K,…...

数据库的联合查询
数据库的联合查询 简介为什么要使⽤联合查询多表联合查询时MYSQL内部是如何进⾏计算的构造练习案例数据案例:⼀个完整的联合查询的过程 内连接语法⽰例 外连接语法 ⽰例⾃连接应⽤场景示例表连接练习 ⼦查询语法单⾏⼦查询多⾏⼦查询多列⼦查询在from⼦句中使⽤⼦查…...

【人工智能】基于PyTorch的深度强化学习入门:从DQN到PPO的实现与解析
《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 深度强化学习(Deep Reinforcement Learning)是一种结合深度学习和强化学习的技术,适用于解决复杂的决策问题。深度Q网络(DQN)和近端策略优化(PPO)是其中两种经典的算法,被广泛应用于游戏、机器人控…...

【深度学习】【RKNN】【C++】模型转化、环境搭建以及模型部署的详细教程
【深度学习】【RKNN】【C】模型转化、环境搭建以及模型部署的详细教程 提示:博主取舍了很多大佬的博文并亲测有效,分享笔记邀大家共同学习讨论 文章目录 【深度学习】【RKNN】【C】模型转化、环境搭建以及模型部署的详细教程前言模型转换--pytorch转rknnpytorch转onnxonnx转rkn…...

CentOS环境上离线安装python3及相关包
0. 准备操作系统及安装包 准备操作系统环境: 首先安装依赖包,安装相应的编译工具 [rootbigdatahost bin]# yum -y install zlib-devel bzip2-devel openssl-devel ncurses-devel sqlite-devel readline-devel tk-devel gdbm-devel db4-devel libpcap-d…...

学习threejs,使用设置bumpMap凹凸贴图创建褶皱,实现贴图厚度效果
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:threejs gis工程师 文章目录 一、🍀前言1.1 ☘️THREE.MeshPhongMaterial高…...

React表单联动
Ant Design 1、dependencies Form.Item 可以通过 dependencies 属性,设置关联字段。当关联字段的值发生变化时,会触发校验与更新。 一种常见的场景:注册用户表单的“密码”与“确认密码”字段。“确认密码”校验依赖于“密码”字段&#x…...

408数据结构:栈、队列和数组选择题做题笔记
408数据结构 第一章 绪论 第二章 线性表 绪论、线性表选择题做题笔记 第三章 栈、队列和数组 栈、队列和数组选择题做题笔记 文章目录 408数据结构前言 一、队列二、栈和队列的应用总结 前言 本篇文章为针对王道25数据结构课后习题的栈、队列和数组的做题笔记,后续…...
sql工具!好用!爱用!
SQLynx的界面设计简洁明了,操作逻辑清晰易懂,没有复杂的图标和按钮,想对哪部分操作就在哪里点击右键,即使你是数据库小白也能轻松上手。 尽管SQLynx是一款免费的工具,但是它的功能却丝毫不逊色于其他付费产品ÿ…...

嵌入式驱动开发详解3(pinctrl和gpio子系统)
文章目录 前言pinctrl子系统pin引脚配置pinctrl驱动详解 gpio子系统gpio属性配置gpio子系统驱动gpio子系统API函数与gpio子系统相关的of函数 pinctrl和gpio子系统的使用设备树配置驱动层部分用户层部分 前言 如果不用pinctrl和gpio子系统的话,我们开发驱动时需要先…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
