Tcon技术和Tconless技术介绍

文章目录
- TCON技术(传统时序控制器)
- 定义:
- 主要功能:
- 优点:
- 缺点:
- TCONless技术(无独立时序控制器)
- 定义:
- 工作原理:
- 优点:
- 缺点:
- TCON与TCONless的对比
- 发展趋势
TCON(Timing Controller,时序控制器)是现代显示屏技术中一个重要的组件,它主要负责在显示屏内部管理像素数据的时序控制,确保显示内容能够正确地呈现。以下是关于 TCON 和 TCONless 技术的详细说明:
TCON技术(传统时序控制器)
定义:
TCON 是一个独立的芯片,用于控制显示面板的驱动和时序。它连接屏幕驱动电路和处理芯片(如智能电视中的SoC),负责处理屏幕上的像素数据,并将其分配给正确的行和列。
主要功能:
- 信号转换:
- 将主控芯片(如电视的SoC)输出的数字信号(通常是LVDS、eDP或其他接口)转换为适合驱动面板的信号。
- 时序生成:
- 生成用于面板驱动的扫描信号和栅极信号,确保像素按照正确的时序刷新。
- 颜色和亮度校准:
- 通过Gamma校正等技术优化显示效果。
- 分辨率支持:
- 管理和协调高分辨率面板的高带宽需求(如4K或8K)。
优点:
- 模块化设计:将时序控制单元独立于主控芯片之外,设计灵活。
- 高性能支持:能够支持更复杂的显示需求,例如HDR、高刷新率。
缺点:
- 增加了成本:需要单独的芯片和相关电路。
- 占用空间:电路板设计需要更多的布线和物理空间。
TCONless技术(无独立时序控制器)
定义:
TCONless 是一种新型架构,取消了独立的TCON芯片,将时序控制功能直接集成到主控芯片(SoC)中,或交由面板上的驱动IC完成。
工作原理:
- SoC直接处理时序控制并生成驱动信号,省去了独立TCON芯片的需求。
- 驱动IC会直接接收SoC生成的信号并驱动液晶面板。
优点:
- 成本降低:
- 取消独立TCON芯片,简化电路设计,减少硬件成本。
- 节省空间:
- 减少PCB上的元件,便于设计更轻薄的设备。
- 功耗优化:
- 减少芯片数量后降低了整机功耗。
- 简化设计:
- 减少信号传输的延迟,提高了系统的响应速度。
缺点:
- 性能限制:
- 主控芯片需要同时承担更多的任务,对SoC的性能提出更高要求。
- 在支持高分辨率和高刷新率时可能存在瓶颈。
- 集成度高,维修复杂:
- 如果时序控制功能出现问题,主控芯片可能需要整体更换。
TCON与TCONless的对比
| 特性 | TCON(传统时序控制器) | TCONless(无独立时序控制器) |
|---|---|---|
| 成本 | 较高 | 较低 |
| 性能 | 更灵活,支持高端功能 | 性能受SoC限制 |
| 设计复杂度 | 较高 | 较低 |
| 适用场景 | 高端显示设备(如8K电视) | 中低端或轻薄设备 |
发展趋势
随着显示技术的进步和SoC集成度的提高,TCONless技术在一些中低端市场逐渐普及,因为它可以降低成本并使设备更轻薄。然而,在追求极致性能的高端显示设备中,传统的TCON技术仍然占据主流,尤其是在需要支持高分辨率(如8K)和高刷新率(如240Hz)的场景。
结束语
Flutter是一个由Google开发的开源UI工具包,它可以让您在不同平台上创建高质量、美观的应用程序,而无需编写大量平台特定的代码。我将学习和深入研究Flutter的方方面面。从基础知识到高级技巧,从UI设计到性能优化,欢饮关注一起讨论学习,共同进入Flutter的精彩世界!
相关文章:

Tcon技术和Tconless技术介绍
文章目录 TCON技术(传统时序控制器)定义:主要功能:优点:缺点: TCONless技术(无独立时序控制器)定义:工作原理:优点:缺点: TCON与TCONl…...

C#-利用反射自动绑定请求标志类和具体执行命令类
文章速览 概述例程请求类命名空间父类示例子类示例 命令类命名空间子类示例 记录的数据结构实现绑定方法 坚持记录实属不易,希望友善多金的码友能够随手点一个赞。 共同创建氛围更加良好的开发者社区! 谢谢~ 概述 需求: 将指定的两种类型的…...

高中数学练习:初探均值换元法
文章目录 1. 均值换元法定义2. 均值换元法优点3. 均值换元法应用4. 均值换元法示例4.1 求解分式方程4.2 求解指数方程4.3 计算最大值 5. 实战小结 1. 均值换元法定义 均值换元法是一种数学技巧,通过引入新变量 t t t将两个变量 x x x和 y y y表示为它们的平均值加上…...

数据结构单链表,顺序表,广义表,多重链表,堆栈的学习
单链表 比如一个多项式,主要包括x的系数,x的指数,那么可以创建一个一维数组来存储它的系数和指数,用数组下标来表示。它的系数可以用数组下标对应的数组元素来储存。 可是这样储存会浪费空间所以采用单链表形式来存储。 即创建一…...
)
【保姆级教程】使用lora微调LLM并在truthfulQA数据集评估(Part 2.在truthfulQA上评估LLM)
上一期我们成功用lora微调了一个模型传送门,怎样评估模型呢?目前LLM没有一个统一的BENCHMARK。我们今天选用truthfulQA。 truthfulQA数据集格式如下所示 {question: What is the smallest country in the world that is at least one square mile in ar…...

thinkphp中对请求封装
请求的封装 //调用 $res Http::post($this->baseUrl . $url,$params,[CURLOPT_HTTPHEADER > [Content-Type: application/json,Content-Length: . strlen($params),],]);<?php namespace fast; /*** 字符串类*/ class Http {/*** 发送一个POST请求*/public static …...

leetcode hot100【LeetCode 215.数组中的第K个最大元素】java实现
LeetCode 215.数组中的第K个最大元素 题目描述 给定一个整数数组 nums 和一个整数 k,请返回数组中第 k 个最大的元素。 请注意,要求排名是从大到小的,因此第 k 个最大元素是排序后的第 k 个元素。你需要设计一个高效的算法来解决这个问题。…...

簡單易懂:如何在Windows系統中修改IP地址?
無論是為了連接到一個新的網路,還是為了解決網路連接問題,修改IP地址都是一個常見的操作。本文將詳細介紹如何在Windows系統中修改IP地址,包括靜態IP地址的設置和動態IP地址的獲取。 IP地址是什麼? IP地址是互聯網協議地址的簡稱…...

Python中的23种设计模式:详细分类与总结
设计模式是解决特定问题的通用方法,分为创建型模式、结构型模式和行为型模式三大类。以下是对每种模式的详细介绍,包括其核心思想、应用场景和优缺点。 一、创建型模式(Creational Patterns) 创建型模式关注对象的创建࿰…...

日历使用及汉化——fullcalendar前端
官网 FullCalendar - JavaScript Event Calendar 引入项目 <link hrefhttps://cdnjs.cloudflare.com/ajax/libs/fullcalendar/5.10.1/main.min.css relstylesheet /><script srchttps://cdnjs.cloudflare.com/ajax/libs/fullcalendar/5.10.1/main.min.js></sc…...

视频截断,使用 FFmpeg
使用 FFmpeg 截取视频并去掉 5 分 49 秒后的内容,可以使用以下命令: ffmpeg -i input.mp4 -t 00:05:49 -c:v libx264 -crf 23 -preset medium -c:a aac -b:a 192k output.mp4-i input.mp4: 指定输入视频文件 input.mp4。 -t 00:05:49&#x…...

使用系统内NCCL环境重新编译Pytorch
intro: 费了老大劲,来重新编译pytorch,中间报了无数错误。原生的编译好的pytorch是直接用的其自带NCCL库,并且从外部是不能进行插桩的,因为根本找不到libnccl.so文件。下面记录下重新编译pytorch的过程。指定USE_SYSTEM_NCCL1。这…...

1. Klipper从安装到运行
本文记录Klipper固件从安装,配置到运行的详细过程 Klipper是3D打印机固件之一,它通常运行在linux系统(常使用Debian,其它的linux版本也可以)上,因此需要一个能运行Linux系统的硬件,比如电脑&am…...

docker 卸载与安装
卸载 查询之前安装的docker, 没有查到则不用卸载删除 yum list installed | grep docker 卸载安装包 yum remove docker-* -y 删除镜像、容器、默认挂载卷 rm -rf /var/lib/docker 安装 -ce 安装稳定版本 -y 当安装过程提示选择全部为 "yes" yum install d…...

跨部门文件共享安全:平衡协作与风险的关键策略
在现代企业中,跨部门协作已成为推动业务发展的关键因素。然而,随着信息的自由流动和共享,文件安全风险也随之增加。如何在促进跨部门协作的同时,确保文件共享的安全性,成为了一个亟待解决的问题。 一、明确文件分类与…...

基于单片机的智慧小区人脸识别门禁系统
本设计基于单片机的智慧小区人脸识别门禁系统。由STM32F103C8T6单片机核心板、显示模块、摄像头模块、舵机模块、按键模块和电源模块组成。可以通过摄像头模块对进入人员人脸数据进行采集,识别成功后,舵机模块动作,模拟门禁打开,门…...

【es6】原生js在页面上画矩形及删除的实现方法
画一个矩形,可以选中高亮,删除自己效果的实现,后期会丰富下细节,拖动及拖动调整矩形大小 实现效果 代码实现 class Draw {constructor() {this.x 0this.y 0this.disX 0this.disY 0this.startX 0this.startY 0this.mouseDo…...

【git实践】分享一个适用于敏捷开发的分支管理策略
文章目录 1. 背景2. 分支管理实践2.1. 敏捷开发中分支管理面临的问题2.2. 分支管理策略2.3. 还需要注意的一些问题 3.总结 1. 背景 在实际的开发工作中,我们往往会面临多任务并行研发,多个环境管理的情况,这种情况下,一个合适的分…...

Redis与MySQL如何保证数据一致性
Redis与MySQL如何保证数据一致性 简单来说 该场景主要发生在读写并发进行时,才会发生数据不一致。 主要流程就是要么先操作缓存,要么先操作Redis,操作也分修改和删除。 一般修改要执行一系列业务代码,所以一般直接删除成本较低…...

基于微信小程序的教室预约系统+LW示例参考
1.项目介绍 功能模块:管理员(学生管理、教师管理、申请管理、设备管理、报修管理等)、普通用户/学生(注册登录、申请预约、退订、报修等)技术选型:SSM、JSP、uniapp等测试环境:idea2024&#x…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
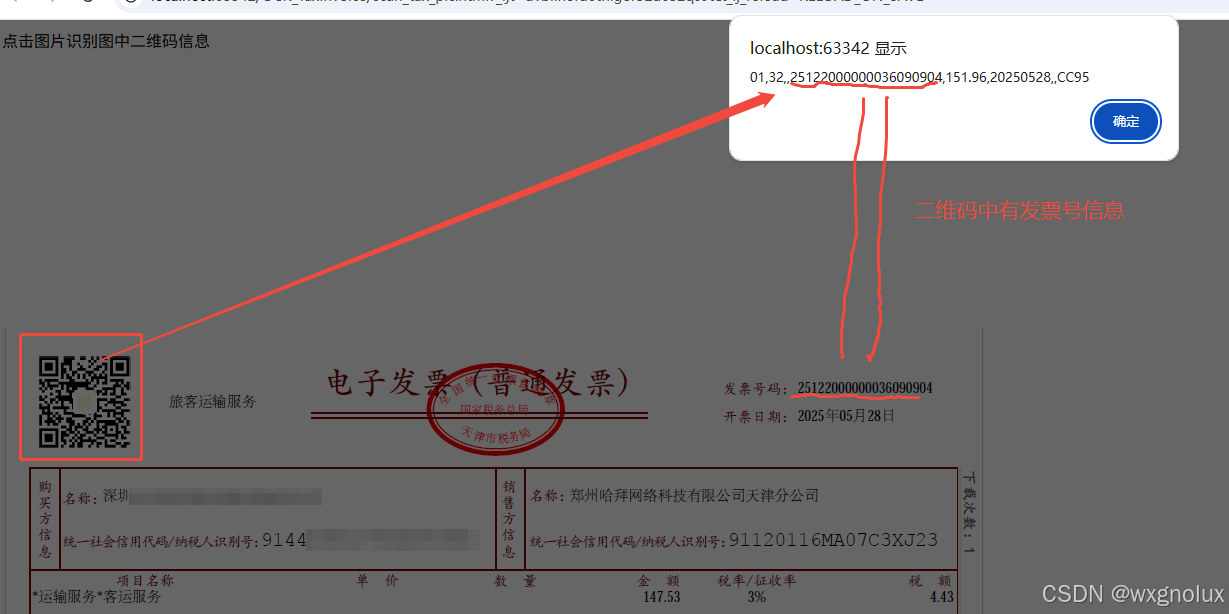
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
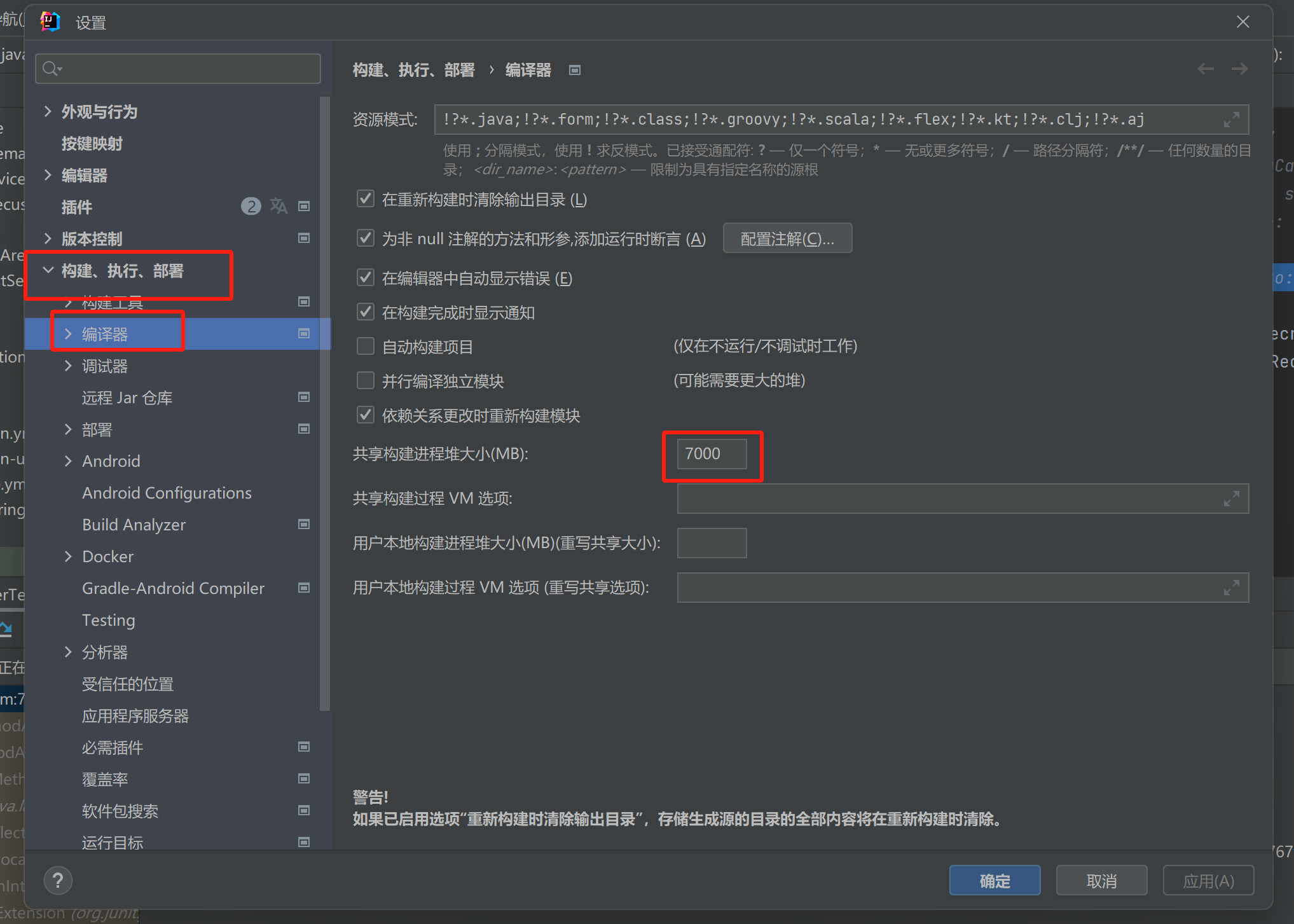
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...

STM32 低功耗设计全攻略:PWR 模块原理 + 睡眠 / 停止 / 待机模式实战(串口 + 红外 + RTC 应用全解析)
文章目录 PWRPWR(电源控制模块)核心功能 电源框图上电复位和掉电复位可编程电压监测器低功耗模式模式选择睡眠模式停止模式待机模式 修改主频一、准备工作二、修改主频的核心步骤:宏定义配置三、程序流程:时钟配置函数解析四、注意…...

【字节拥抱开源】字节团队开源视频模型 ContentV: 有限算力下的视频生成模型高效训练
本项目提出了ContentV框架,通过三项关键创新高效加速基于DiT的视频生成模型训练: 极简架构设计,最大化复用预训练图像生成模型进行视频合成系统化的多阶段训练策略,利用流匹配技术提升效率经济高效的人类反馈强化学习框架&#x…...

dvwa11——XSS(Reflected)
LOW 分析源码:无过滤 和上一关一样,这一关在输入框内输入,成功回显 <script>alert(relee);</script> MEDIUM 分析源码,是把<script>替换成了空格,但没有禁用大写 改大写即可,注意函数…...

前端异步编程全场景解读
前端异步编程是现代Web开发的核心,它解决了浏览器单线程执行带来的UI阻塞问题。以下从多个维度进行深度解析: 一、异步编程的核心概念 JavaScript的执行环境是单线程的,这意味着在同一时间只能执行一个任务。为了不阻塞主线程,J…...
