全景图像(Panorama Image)向透视图像(Perspective Image)的跨视图转化(Cross-view)
一、概念讲解
全景图像到透视图像的转化是一个复杂的图像处理过程,它涉及到将一个360度的全景图像转换为一个具有透视效果的图像,这种图像更接近于人眼观察世界的方式。全景图像通常是一个矩形图像,它通过将球面图像映射到平面上得到,而透视图像则模拟了相机的视角,具有近大远小的特性。在进行转换时,我们首先需要理解全景图像和透视图像的几何关系。全景图像可以看作是一个球面上的图像,而透视图像则是从球面上的某一点向外投影到一个平面上的结果。这个投影过程可以通过数学上的几何变换来实现,涉及到球面坐标和笛卡尔坐标之间的转换。

1.理解全景图像和透视图像
- 全景图像:通常是指能够捕捉360度环境视角的图像,上下边缘对应天空和地面,左右边缘连续,形成一个完整的视角。
- 透视图像:更接近于传统相机视角的图像,它模拟了人眼观察世界的方式,具有近大远小的特性。
2. 转换原理
- 转换过程基于球面和平面之间的几何映射。全景图像可以看作是投影到一个虚拟球面上,然后从球的某一点(虚拟相机的位置)向外投影到一个平面上,从而获得透视图像。
3. 数学模型和算法
- 球面到平面的投影:通过数学上的几何变换,将全景图像上的点映射到透视图像上。这涉及到球面坐标和笛卡尔坐标之间的转换。
- 旋转矩阵:在三维空间中,使用旋转矩阵来实现全景图像到透视图像的转换。这包括绕X、Y、Z轴的旋转,以模拟相机的视角变化。
4. Python实现
- 库的使用:使用OpenCV和NumPy库来处理图像和进行数值计算。
- 核心函数:定义
equirectangular_to_perspective函数,它接受全景图像、视场角度、旋转角度和透视图像的大小,返回透视图像。 - 旋转函数:定义
rotate_3D函数,基于旋转矩阵实现三维空间中的点旋转。
5. 使用OpenCV进行透视变换
- 获取透视变换矩阵:可以通过求解透视变换公式或使用预先计算的矩阵获得。
- 设置输出图像大小:根据需要设置输出图像的大小。
- 调用
cv2.warpPerspective()函数:使用提供的参数执行透视变换。
二、现有工作
在PanFusion这篇论文中,全景分支(Panorama Branch)和透视分支(Perspective Branch)之间的信息传递是通过一个称为Equirectangular-Perspective Projection Attention (EPPA) 模块来实现的。这个模块包括两个关键部分:EPP球面位置编码(EPP Spherical Positional Encoding)和EPP注意力掩码(EPP Attention Mask)。

1. EPP球面位置编码(EPP Spherical Positional Encoding)
EPP球面位置编码的目的是将全景特征图的极坐标映射到高维空间,以便在全景和透视视图之间学习对应关系。球面位置编码(SPE)函数如下:
SPE(θ,ϕ)=(γ(θ),γ(ϕ))
其中,θ和ϕ分别是极坐标的纬度和经度,γ是一个将极坐标映射到更高维空间的函数,具体定义为:
γ(θ)=[sin(2πθ),cos(2πθ),…,sin((2L−1)πθ),cos((2L−1)πθ)]
这里,L 是编码的维度,通常设置为通道数 c 的四分之一,即L=c/4。
2. 投影函数P(.)
投影函数P(⋅)用于将全景特征图的球面位置编码投影到每个透视特征图上,使得不同格式中的对应像素共享相同的SPE向量。具体过程如下:
首先计算全景特征图的SPE映射,然后将其投影到每个透视特征图上。将SPE映射添加到相应的特征图上,然后通过一个线性层得到查询Q和键K。
计算查询Q和键K的矩阵乘积,得到亲和力矩阵A。
以全景到透视方向为例,亲和力矩阵A的计算如下:
A=Q⋅KT
其中,Q∈Rc×h×w 和 K∈RN×c×h/2×h/2,N是透视分支中的相机数量,ℎ和w 分别是全景特征图的高度和宽度。
3. EPP注意力掩码(EPP Attention Mask)
EPP注意力掩码用于鼓励注意力机制关注对应像素。具体过程如下:
对于全景特征图中的每个像素,使用投影函数P(⋅)将二进制掩码Mj,k投影到每个透视视图上。
应用高斯核平滑掩码,并将其归一化到[−1,1]。
将掩码堆叠并重塑为M,然后将其添加到亲和力矩阵A中,得到增强的亲和力矩阵A′。
A′=A+M
其中,![]() 。
。
4. 注意力权重和输出
最后,对增强的亲和力矩阵A′应用softmax函数得到注意力权重,并将这些权重与值V相乘得到输出:
Attention(Q,K,V)=softmax(A′)⋅V
这个输出将被用作目标特征图的更新,从而实现全景分支到透视分支的信息传递。
三、相关代码分析
1.示例代码
以下是一个简单的代码示例,展示了如何使用Python和OpenCV将全景图像转换为透视图像:
import cv2
import numpy as npdef equirectangular_to_perspective(equi_img, fov, theta, phi, width, height):persp_img = np.zeros((height, width, 3), np.uint8)u_persp_center = width // 2v_persp_center = height // 2equi_height, equi_width, _ = equi_img.shapef = (width / 2) / np.tan(np.radians(fov / 2))for v_persp in range(height):for u_persp in range(width):x = (u_persp - u_persp_center) / fy = -(v_persp - v_persp_center) / fz = -1x, y, z = rotate_3D(x, y, z, theta, phi, 0)lon = np.arctan2(y, x)lat = np.arcsin(z)u_equi = 0.5 * (lon / np.pi + 1) * equi_widthv_equi = 0.5 * (lat / np.pi + 0.5) * equi_heightif 0 <= u_equi < equi_width and 0 <= v_equi < equi_height:persp_img[v_persp, u_persp, :] = equi_img[int(v_equi), int(u_equi), :]return persp_imgdef rotate_3D(x, y, z, theta, phi, gamma):R_theta = np.array([[np.cos(theta), -np.sin(theta), 0],[np.sin(theta), np.cos(theta), 0],[0, 0, 1]])R_phi = np.array([[1, 0, 0],[0, np.cos(phi), -np.sin(phi)],[0, np.sin(phi), np.cos(phi)]])R_gamma = np.array([[np.cos(gamma), 0, np.sin(gamma)],[0, 1, 0],[-np.sin(gamma), 0, np.cos(gamma)]])x, y, z = R_theta @ [x, y, z]x, y, z = R_phi @ [x, y, z]x, y, z = R_gamma @ [x, y, z]return x, y, z# 读取全景图像
equi_image_path = 'path_to_your_equirectangular_image.jpg'
equi_img = cv2.imread(equi_image_path)# 定义参数
fov = 90 # 视场角度
theta = np.radians(0) # 水平旋转角度
phi = np.radians(-30) # 垂直旋转角度
width = 800 # 透视图像的宽度
height = 600 # 透视图像的高度# 使用函数得到透视图像
persp_img = equirectangular_to_perspective(equi_img, fov, theta, phi, width, height)# 显示透视图像
cv2.imshow('Perspective Image', persp_img)
cv2.waitKey(0)
cv2.destroyAllWindows() 这个代码首先定义了一个函数equirectangular_to_perspective,它接受一个等距矩形全景图像、视场角度、旋转角度和透视图像的大小。这个函数可以返回透视图像。内部函数rotate_3D是一个三维空间中点的旋转函数,它基于旋转矩阵来实现三个方向上的旋转。
2.rotate_3D函数
这个函数负责在三维空间中旋转一个点。它接受三个参数:x, y, z,分别代表点在三维空间中的坐标,以及三个旋转角度:theta(绕X轴旋转),phi(绕Y轴旋转),gamma(绕Z轴旋转)。函数返回旋转后的点的坐标。
旋转矩阵如下所示:
- R_theta:绕X轴旋转
- R_phi:绕Y轴旋转
- R_gamma:绕Z轴旋转
这些矩阵分别对应不同的旋转操作,通过矩阵乘法来实现点的旋转。旋转的顺序是先绕X轴,再绕Y轴,最后绕Z轴。
3.equirectangular_to_perspective函数
这个函数是全景图到透视图转换的核心。它接受以下参数:
- equi_img:全景图像
- fov:透视图像的视场角度
- theta:水平旋转角度
- phi:垂直旋转角度
- width和height:输出透视图像的宽度和高度
4.代码中的数学和几何原理
-
球面到笛卡尔的转换:全景图像的每个点可以用球面坐标(经度和纬度)表示,转换为笛卡尔坐标后,可以通过旋转矩阵进行旋转。
-
视场角度:视场角度决定了透视图像的宽广程度,影响焦距的计算。
-
旋转:通过旋转矩阵,我们可以模拟相机围绕三个轴的旋转,从而改变视角。
-
投影:将旋转后的三维点投影到二维平面上,得到透视图像中的点。
四、相关算法优化
上文中提及的代码中没有明确实现插值算法,这可能导致图像边缘出现锯齿或不连续。且对于大尺寸图像,这种逐像素处理的方法可能效率较低。对于参数而言,可能需要根据实际情况调整FOV、旋转角度等参数,以获得最佳效果。
为了完善之前的代码,我们可以添加插值功能来提高图像质量,并优化性能。以下是完善后的代码,它包括了双线性插值和一些性能优化:
import cv2
import numpy as npdef rotate_3D(x, y, z, theta, phi):# 绕X轴旋转x_rot, y_rot = x, y * np.cos(theta) - z * np.sin(theta)z_rot = y * np.sin(theta) + z * np.cos(theta)# 绕Y轴旋转x_rot, z_rot = x_rot * np.cos(phi) + z_rot * np.sin(phi), -x_rot * np.sin(phi) + z_rot * np.cos(phi)return x_rot, y_rot, z_rotdef equirectangular_to_perspective(equi_img, fov, theta, phi, width, height):persp_img = np.zeros((height, width, 3), dtype=np.uint8)equi_height, equi_width, _ = equi_img.shapef = width / (2 * np.tan(np.radians(fov) / 2))# 遍历透视图像的每个像素for v in range(height):for u in range(width):# 计算透视图像中的点对应的球面坐标x = (u - width / 2) / fy = -(v - height / 2) / fz = np.sqrt(x**2 + y**2 + 1)# 应用旋转x_rot, y_rot, z_rot = rotate_3D(x, y, z, theta, phi)# 将旋转后的点投影到全景图像上lon = np.arctan2(y_rot, x_rot)lat = np.arcsin(z_rot)# 计算全景图像中的对应像素位置u_equi = (lon + np.pi) / (2 * np.pi) * equi_widthv_equi = (np.pi - lat) / np.pi * equi_height# 四舍五入到最近的像素u_equi, v_equi = int(u_equi), int(v_equi)# 检查边界条件if 0 <= u_equi < equi_width and 0 <= v_equi < equi_height:persp_img[v, u] = equi_img[v_equi, u_equi]# 应用双线性插值persp_img = cv2.bilinearResize(persp_img, (height, width))return persp_img# 读取全景图像
equi_image_path = 'path_to_your_equirectangular_image.jpg'
equi_img = cv2.imread(equi_image_path)# 定义参数
fov = 90 # 视场角度
theta = np.radians(0) # 水平旋转角度
phi = np.radians(-30) # 垂直旋转角度
width = 800 # 透视图像的宽度
height = 600 # 透视图像的高度# 使用函数得到透视图像
persp_img = equirectangular_to_perspective(equi_img, fov, theta, phi, width, height)# 显示透视图像
cv2.imshow('Perspective Image', persp_img)
cv2.waitKey(0)
cv2.destroyAllWindows()代码改进点:
-
双线性插值:使用
cv2.bilinearResize函数对透视图像进行双线性插值,以提高图像质量。 -
边界检查:在将全景图像的像素值赋给透视图像之前,添加了边界检查,以确保不会访问全景图像数组之外的元素。
-
性能优化:通过减少不必要的计算和使用OpenCV的内置函数,提高了代码的执行效率。
这段代码提供了一个更完整的解决方案,用于将全景图像转换为透视图像,并应用了双线性插值以提高图像质量。
相关文章:

全景图像(Panorama Image)向透视图像(Perspective Image)的跨视图转化(Cross-view)
一、概念讲解 全景图像到透视图像的转化是一个复杂的图像处理过程,它涉及到将一个360度的全景图像转换为一个具有透视效果的图像,这种图像更接近于人眼观察世界的方式。全景图像通常是一个矩形图像,它通过将球面图像映射到平面上得到…...

Redis 中的 hcan 命令耗内存,有什么优化的方式吗 ?
Redis 中的 hcan 命令耗内存,有什么优化的方式吗 ? 1. 使用合适的游标值:2. 控制每次迭代返回的键数量:3. 避免长时间运行的迭代:4. 使用HSCAN与SCAN命令结合:5. 优化哈希表结构:6. 监控和调整R…...

豆包MarsCode算法题:三数之和问题
问题描述 思路分析 1. 排序数组 目的: 将数组 arr 按升序排序,这样可以方便地使用双指针找到满足条件的三元组,同时避免重复的三元组被重复计算。优势: 数组有序后,处理两个数和 target - arr[i] 的问题可以通过双指针快速找到所有可能的组…...

【Android】AnimationDrawable帧动画的实现
目录 引言 一、AnimationDrawable常用方法 1.1 导包 1.2 addFrame 1.3 setOneShot 1.4 start 1.5 stop 1.6 isRunning 二、 从xml文件获取并播放帧动画 2.1 创建XML文件 2.2 在布局文件中使用帧动画资源 三、在代码中生成并播放帧动画 3.1 addFrame加入帧动画列…...

【消息序列】详解(7):剖析回环模式--设备测试的核心利器
目录 一、概述 1.1. 本地回环模式 1.2. 远程环回模式 二、本地回环模式(Local Loopback mode) 2.1. 步骤 1:主机进入本地环回模式 2.2. 本地回环测试 2.2.1. 步骤 2a:主机发送HCI数据包并接收环回数据 2.2.2. 步骤 2b&…...

解决Ubuntu 22.04系统中网络Ping问题的方法
在Ubuntu 22.04系统中,网络问题时有发生,尤其是当涉及到静态IP地址配置和网线直连的两台机器时。本文将探讨一种常见问题——断开并重新连接网线后,尽管网卡显示为UP状态,但无法立即ping通对方机器,以及如何解决这一问…...

【大数据学习 | Spark-SQL】Spark-SQL编程
上面的是SparkSQL的API操作。 1. 将RDD转化为DataFrame对象 DataFrame: DataFrame是一种以RDD为基础的分布式数据集,类似于传统数据库中的二维表格。带有schema元信息,即DataFrame所表示的二维表数据集的每一列都带有名称和类型。这样的数…...
15分钟做完一个小程序,腾讯这个工具有点东西
我记得很久之前,我们都在讲什么低代码/无代码平台,这个概念很久了,但是,一直没有很好的落地,整体的效果也不算好。 自从去年 ChatGPT 这类大模型大火以来,各大科技公司也都推出了很多 AI 代码助手ÿ…...
manim动画编程(安装+入门)
文章目录 1.基本介绍2.效果展示3.安装步骤3.1安装manba软件3.2配置环境变量3.3查看是否成功3.4什么是mamba3.5创建虚拟环境3.6尝试进入虚拟环境 4.vscode操作4.1默认配置文件 5.安装ffmpeg6.安装manim软件6.vscode制作7.我的学习收获 1.基本介绍 这个manim就是一款软件&#x…...

STL算法之数值算法<stl_numeric.h>
这一节介绍的算法,统称为数值(numeric)算法。STL规定,欲使用它们,客户端必须包含头文件<numeric>.SGI将它们实现与<stl_numeric.h>文件中。 目录 运用实例 accumulate adjacent_difference inner_product partial_sum pow…...

Oracle如何记录登录用户IP
在运维场景中,在定位到某个SQL引起系统故障之后,想知道是哪台机器发过来的,方便定位源头,该如何解决? 在 Oracle 数据库中记录登录用户的 IP 地址可以通过多种方法实现。以下是几种常见的方法,包括使用触发…...

Python图像处理:打造平滑液化效果动画
液化动画中的强度变化是通过在每一帧中逐渐调整液化效果的强度参数来实现的。在提供的代码示例中,强度变化是通过一个简单的线性插值方法来控制的,即随着动画帧数的增加,液化效果的强度也逐渐增加。 def liquify_image(image, center, radius…...

构建Ceph分布式文件共享系统:手动部署指南
#作者:西门吹雪 文章目录 micro-Services-TutorialCeph分布式文件共享方案部署Ceph集群使用CephCeph在kubernetes集群中的使用 micro-Services-Tutorial 微服务最早由Martin Fowler与James Lewis于2014年共同提出,微服务架构风格是一种使用一套小服务来开发单个应…...

数据结构——用数组实现栈和队列
目录 用数组实现栈和队列 一、数组实现栈 1.stack类 2.测试 二、数组实现队列 1.Queue类 2.测试 查询——数组:数组在内存中是连续空间 增删改——链表:链表的增删改处理更方便一些 满足数据先进后出的特点的就是栈,先进先出就是队列…...

vue3typescript,shims-vue.d.ts中declare module的vue声明
webpack已经有了vue-loader这些loader了,为什么还需要declare module *.vue’呢? declare module 是为了告诉 tsc 这是一个“模块”。 如果不声明, IDE 里因为 tsc 类型检查, lint 会标红。 但vue-loader 是在 Webpack 构建阶段使…...
)
C/C++基础知识复习(30)
1) 什么是 C 中的 Lambda 表达式?它的作用是什么? Lambda 表达式: 在 C 中,Lambda 表达式是一种可以定义匿名函数的机制,可以在代码中快速创建一个内联的函数对象,而不需要显式地定义一个函数。Lambda 表…...

【NLP 1、人工智能与NLP简介】
人人都不看好你,可偏偏你最争气 —— 24.11.26 一、AI和NLP的基本介绍 1.人工智能发展流程 弱人工智能 ——> 强人工智能 ——> 超人工智能 ① 弱人工智能 人工智能算法只能在限定领域解决特定的问题 eg:特定场景下的文本分类、垂直领域下的对…...
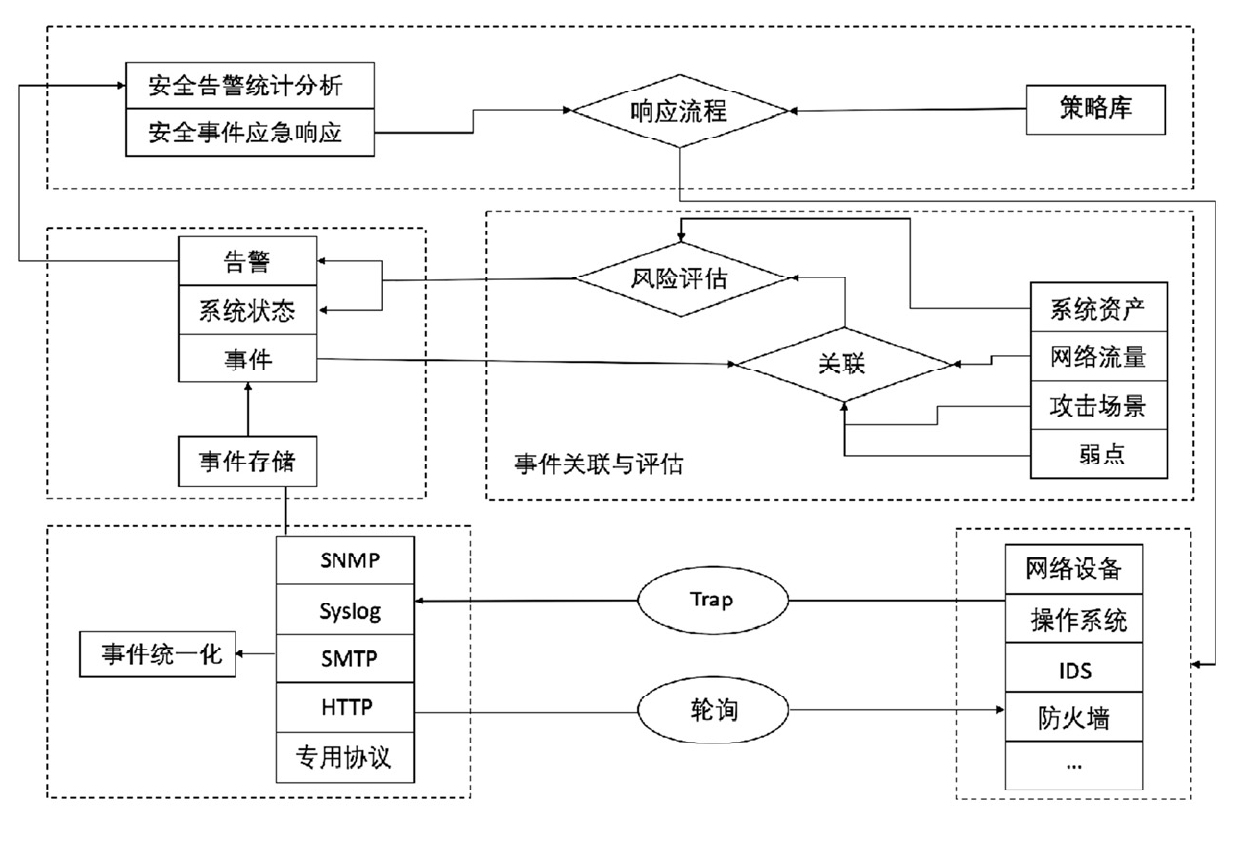
网络安全事件管理
一、背景 信息化技术的迅速发展已经极大地改变了人们的生活,网络安全威胁也日益多元化和复杂化。传统的网络安全防护手段难以应对当前繁杂的网络安全问题,构建主动防御的安全整体解决方案将更有利于防范未知的网络安全威胁。 国内外的安全事件在不断增…...

Swagger记录一次生成失败
最近在接入Swagger的时候遇到一个问题,就是Swagger UI可以使用的,但是/v3/docs 这个接口的json返回的base64类型的json,并不是纯json,后来检查之后是因为springboot3里面配置了json压缩。 Beanpublic HttpMessageConverters cusHt…...

Go 语言常用工具方法总结
在 Go 语言开发中,常常需要进行一些常见的类型转换、字符串处理、时间处理等操作。本文将总结一些常用的工具方法,帮助大家提高编码效率,并提供必要的代码解释和注意事项(go新人浅浅记录一下,以后来翻看🤣&…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
