当前位置：首页 > news >正文

电机瞬态分析基础（7）：坐标变换（3）αβ0变换，dq0变换

news 2025/9/13 9:37:20

1. 三相静止坐标系与两相静止坐标系的坐标变换―αβ0坐标变换

若上述x、y坐标系在空间静止不动，且x轴与A轴重合，即 $\theta =0$ ，如图1所示，则为两相静止坐标系，常称为 $\alpha \beta$ 坐标系，考虑到零轴分量，也称为αβ0坐标系。

图1. ABC坐标系与 $\alpha \beta$ 坐标系

从三相静止坐标系到两相静止坐标系的变换称为三相-两相变换，简称3/2变换。由下式，

$\left[ \begin{array}{c} i_A \\ i_B \\ i_C \end{array} \right] = \left[ \begin{array}{ccc} \cos\theta & -\sin\theta & 1 \\ \cos(\theta - 120^\circ) & -\sin(\theta - 120^\circ) & 1 \\ \cos(\theta + 120^\circ) & -\sin(\theta + 120^\circ) & 1 \end{array} \right] \left[ \begin{array}{c} i_x \\ i_y \\ i_0 \end{array} \right] = \mathbf{C}_{2r/3s} \left[ \begin{array}{c} i_x \\ i_y \\ i_0 \end{array} \right]$

令 $\theta =0$ 可得

$\left[ \begin{array}{c} i_a \\ i_\beta \\ i_0 \end{array} \right] = \frac{2}{3} \left[ \begin{array}{ccc} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{array} \right] \left[ \begin{array}{c} i_A \\ i_B \\ i_C \end{array} \right]$ (1)

令 $C_{3/2}$ 表示从三相静止坐标系到两相静止坐标系的变换矩阵，则

$\mathbf{C}_{3/2} = \frac{2}{3} \left[ \begin{array}{ccc} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{array} \right]$ (2)

相应地，从两相坐标系到三相坐标系的变换矩阵为

$\mathbf{C}_{2/3} = \mathbf{C}_{3/2}^{-1} = \left[ \begin{array}{ccc} 1 & 0 & 1 \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} & 1 \\ -\frac{1}{2} & -\frac{\sqrt{3}}{2} & 1 \end{array} \right]$ (3)

式（2）和式（3）不满足功率不变约束。由上一节式（9），令 $\theta =0$ 可得满足功率不变约束的从三相静止坐标系到两相静止坐标系的变换矩阵

$\mathbf{C}_{3/2} = \sqrt{\frac{2}{3}} \left[ \begin{array}{ccc} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right]$ （4）

相应地，从两相坐标系到三相坐标系满足功率不变约束的变换矩阵为

$\mathbf{C}_{2/3} = \mathbf{C}_{3/2}^{-1} = \mathbf{C}_{3/2}^T = \sqrt{\frac{2}{3}} \left[ \begin{array}{ccc} 1 & 0 & \frac{1}{\sqrt{2}} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} & \frac{1}{\sqrt{2}} \\ -\frac{1}{2} & -\frac{\sqrt{3}}{2} & \frac{1}{\sqrt{2}} \end{array} \right]$ （5）

在实际应用中，上述坐标变换关系常可进一步简化。例如，在交流调速系统中，交流电机通常为中性点隔离的三相星型连接（Y接），有 $i_{A}+i_{B}+i_{C}=0$ ，则 $i_{0}=0$ ，因此可将零轴分量去掉。同时，由于三相电流中只有两相独立，三相系统中的电流可以只用 $i_{A}$ 、 $i_{B}$ 表达，而将C相电流用 $i_{C}=-(i_{A}+i_{B})$ 代入。相应的坐标变换关系简化为

$\left[ \begin{array}{c} i_\alpha \\ i_\beta \end{array} \right] = \left[ \begin{array}{cc} 1 & 0 \\ \frac{1}{\sqrt{3}} & \frac{2}{\sqrt{3}} \end{array} \right] \left[ \begin{array}{c} i_A \\ i_B \end{array} \right] \text{or} \left[ \begin{array}{c} i_\alpha \\ i_\beta \end{array} \right] = \left[ \begin{array}{cc} \sqrt{\frac{2}{3}} & 0 \\ \frac{1}{\sqrt{2}} & \sqrt{2} \end{array} \right] \left[ \begin{array}{c} i_A \\ i_B \end{array} \right]$ (6)

以及

$\left[ \begin{array}{c} i_A \\ i_B \end{array} \right] = \left[ \begin{array}{cc} 1 & 0 \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \end{array} \right] \left[ \begin{array}{c} i_\alpha \\ i_\beta \end{array} \right] \text{or} \left[ \begin{array}{c} i_\alpha \\ i_\beta \end{array} \right] = \left[ \begin{array}{cc} \sqrt{\frac{2}{3}} & 0 \\ -\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} \end{array} \right] \left[ \begin{array}{c} i_A \\ i_B \end{array} \right]$ （7）

可见，三相/两相变换（3/2变换）是任意速xy0坐标系当其转速等于零时的特例。3/2变换是静止坐标系之间的变换，因此其变换矩阵中所有元素均与坐标旋转角 $\theta$ 无关，都是常数。

隐极三相交流电机的定子和转子的电感矩阵，经过 $\alpha \beta 0$ 变换将成为对角矩阵。因为，从三相变为两相系统后，由于 $\alpha$ 轴和 $\beta$ 轴在空间互相垂直，互感为零，而零序又是一个孤立的系统，所以

$\alpha$ 、 $\beta$ 、0三根轴线之间达到“解耦”。这一点，以后在感应电机的分折中将会用到。

2. 三相静止坐标系与两相转子速旋转坐标系的坐标变换―dq0坐标变换

图2. $dq0$ 坐标变换

$dq0$ 坐标系是一种与转子一起旋转的两相坐标系和零序系统的组合。若转子为凸极，则 $d$ 轴(直轴)通常与凸极的中心轴线重合， $q$ 轴(交轴)超前于 $d$ 轴90“电角，如图2所示。 $dq0$ 变换是从静止的ABC坐标系变换到转子速旋转的 $dq0$ 坐标系的一种变换。 $dq0$ 分量首先由帕克(Park)提出．所以亦称为帕克分量。显然， $dq0$ 坐标变换的变换矩阵在形式上与 $xy0$ 坐标变换的变换矩阵完全相同，

只不过， $dq0$ 坐标系是一种与转子一起旋转的坐标系，而 $xy0$ 坐标系是一种以任意速旋转的坐标系。可见， $dq0$ 坐标系是任意速 $xy0$ 坐标系当其转速等于转子速时的特例，当然， $\alpha \beta 0$ 坐标系也是

$xy0$ 坐标系当其转速等于零时的特例。

$dq0$ 坐标变换主要用于凸极同步电机的瞬态分析中，在转速为常值和磁路为线性的条件下，它可以把含有时变系数的自感和互感所组成的定子电感矩阵，通过坐标变换，变成元素为常数的对角线矩阵，达到“解耦”和“元素常数化”的目的，使凸极电机的分析大为简化。

$\alpha \beta 0$ 坐标变换和 $dq0$ 坐标变换是电机瞬态分析中最常用的坐标变换。

电机瞬态分析基础（7）：坐标变换（3）αβ0变换，dq0变换

1. 三相静止坐标系与两相静止坐标系的坐标变换―αβ0坐标变换

2. 三相静止坐标系与两相转子速旋转坐标系的坐标变换―dq0坐标变换

相关文章：

电机瞬态分析基础（7）：坐标变换（3）αβ0变换，dq0变换

Open3D (C++) 生成任意3D椭圆点云

5.利用Pandas以及Numpy进行数据清洗

@Bean注解详细介绍以及应用

基于SpringBoot的预制菜销售系统

从 EXCEL 小白到 EXCEL 高手的成长之路

【纸飞机串口调试工具】数值显示器及四则运算

浅谈volatile

Python3 爬虫 Scrapy的使用

多线程篇-4--重点概念1（volatile，Synchronized，内存屏障，MESI协议）

本地学习axios源码-如何在本地打印axios里面的信息

1、SpringBoo中Mybatis多数据源动态切换

【浏览器】缓存与存储

积鼎科技携手西北工业大学动力与能源学院共建复杂多相流仿真联合实验室

5. langgraph实现高级RAG (Adaptive RAG)

Postman设置接口关联，实现参数化

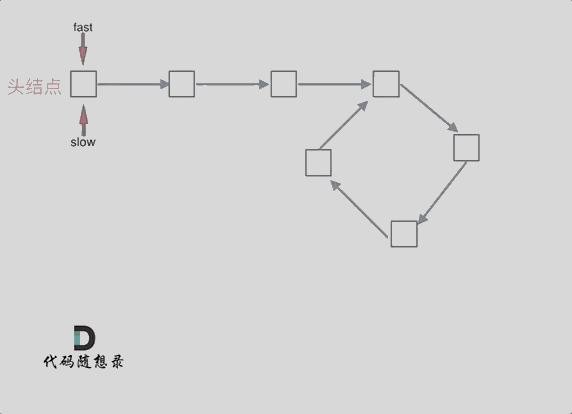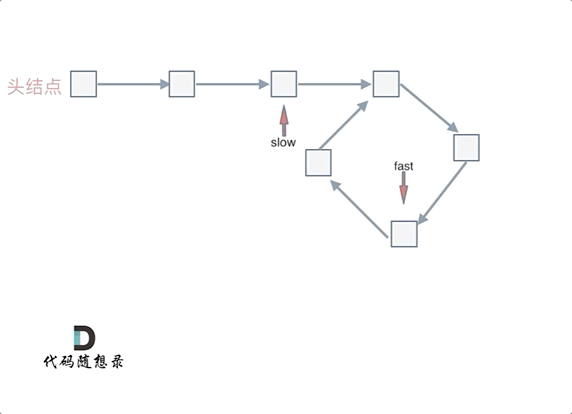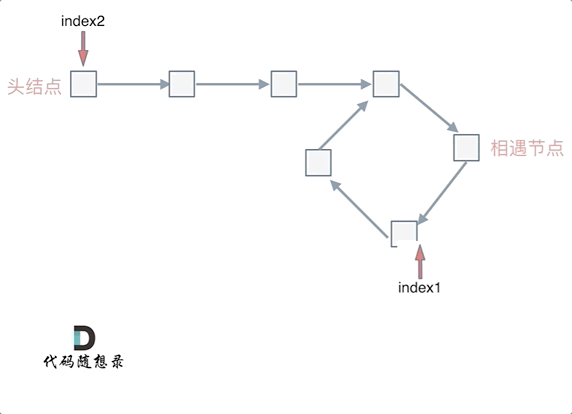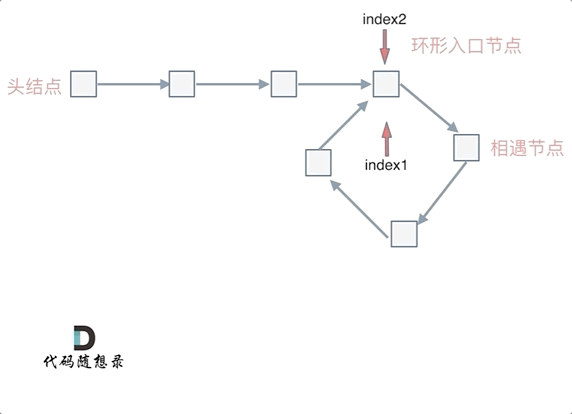
代码随想录day02--链表

杰发科技AC7803——不同晶振频率时钟的配置

ArcGIS栅格影像裁剪工具

【查询目录】.NET开源 ORM 框架 SqlSugar 系列

Redis相关知识总结（缓存雪崩，缓存穿透，缓存击穿，Redis实现分布式锁，如何保持数据库和缓存一致）

剑指offer20_链表中环的入口节点

Element Plus 表单(el-form)中关于正整数输入的校验规则

JVM 内存结构详解

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能

uniapp 集成腾讯云 IM 富媒体消息（地理位置/文件）

[拓扑优化] 1.概述

高保真组件库：开关

【Java】Ajax 技术详解

使用python进行图像处理—图像滤波（5）