交换排序----快速排序

快速排序

快速排序是一种高效的排序算法，它采用分治法策略，将数组分为较小和较大的两个子数组，然后递归排序两个子数组。

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

快速排序递归实现的主框架与二叉树前序遍历规则非常像，我们在写递归框架时可想想二叉树前序遍历规则即可快速写出来，后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。而将区间按照基准值划分为左右两半部分的常见方式有：hoare版本、挖坑法、前后指针版本。

hoare版本

讲解

接下来我们一起看一下hoare版本的快速排序是如何实现的：

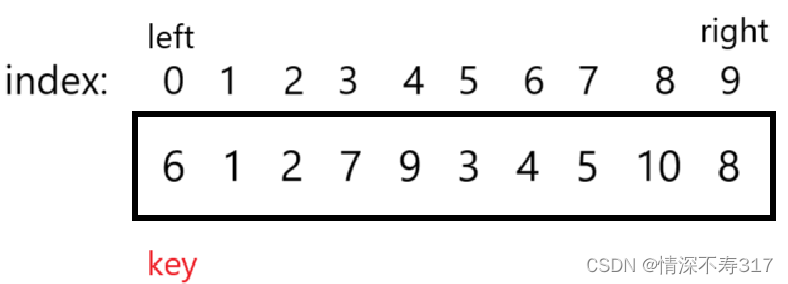
 选数组左端点为基准值（key）初始位置。

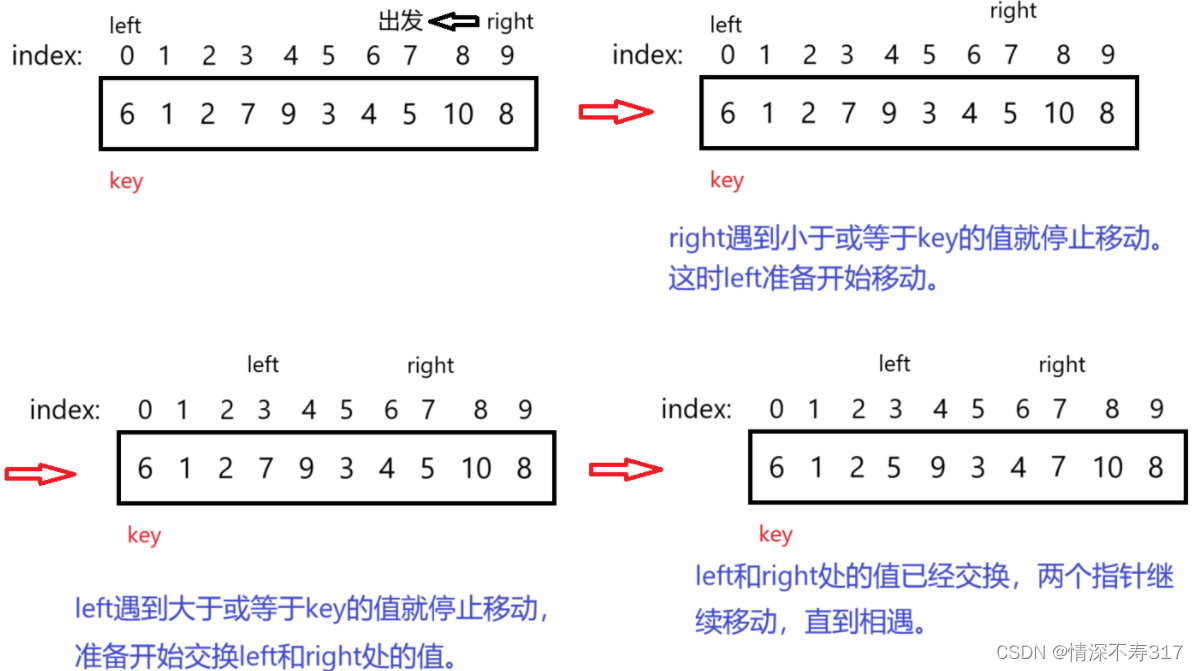
用双指针从两端向中间移动（这里需要注意，如果选数组左端的值为key，则右指针先走；如果选数组右端的值为key，则左指针先走。）。左指针遇到大于或等于key的值就停，右指针遇到小于或等于key的值就停。停后交换两指针所指元素，继续移动，直到相遇：

 这里补充一个结论：left和right相遇的值一定是小于等于key的。为什么呢？这里有三种情况：①当right向左移动找小于或等于key的值，left向右移动找大于或等于key的值却没找到，而这时left和right相遇了，此时相遇的位置肯定比key小或相等；②当right向左移动找小于或等于key的值，但是没找到就直接遇到left，那这里的left肯定就在key值的位置上，那它们就在key值相遇，这就是等于key值的情况；③right向左移动时找到了小于或等于key的值，left向右移动占到了大于或等于key的值，left和right位置上的值交换，然后right继续向左移动找小于或等于key的值，但是right已经找不到小于或等于key的值了，那它就会与left相遇，此时left上的值是刚刚从right位置上交换过来的小于或等于key的值，所以他们还是在小于或等于key上的值相遇。

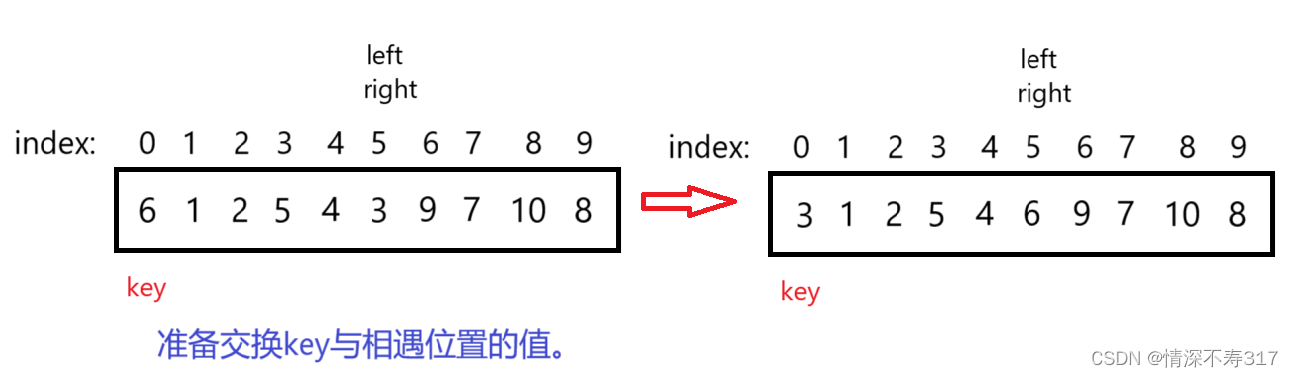
 指针相遇后，交换key与相遇位置值。

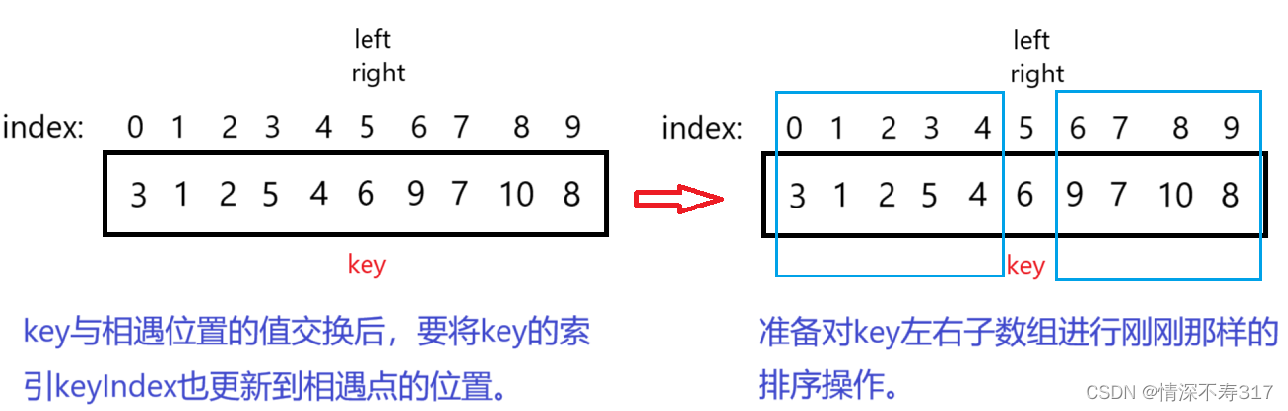
 key的索引要更新到相遇点，接下来准备对key左右子数组分别进行重复的操作。

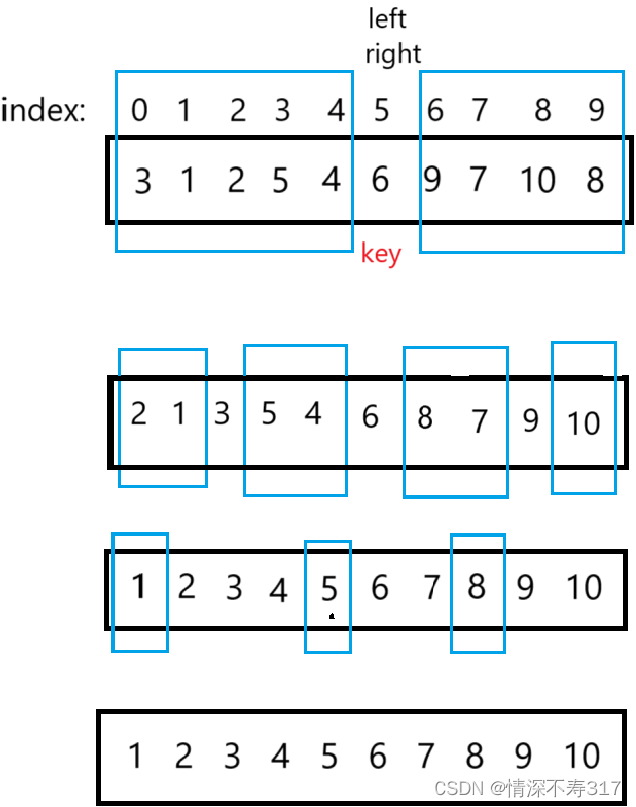 我们发现，整体看每次对key左右子数组的排序很像二叉树结构，所以我们可以通过递归完成对子区间数据的排序。

代码

void swap(int* x, int* y) {int tmp = *x;*x = *y;*y = tmp;
}int hoare(int* a, int left, int right)
{int keyIndex = left;while (left < right){while (left < right && a[keyIndex] <= a[right]){--right;}while (left < right && a[keyIndex] >= a[left]){++left;}swap(&a[left], &a[right]);}swap(&a[keyIndex], &a[right]);keyIndex = right;return keyIndex;
}void quickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;int keyIndex = hoare(a, left, right);quickSort(a, begin, keyIndex - 1);quickSort(a, keyIndex + 1, end);}

在代码中有两个点要注意：hoare函数里的最内层的两个while循环中必须要有left<right这个条件,不然会越界；while (left < right && a[keyIndex] <= a[right])不能写成while (left < right && a[keyIndex] < a[right])，while (left < right && a[keyIndex] >= a[left])不能写成 while (left < right && a[keyIndex] > a[left])，不然出现与key一样的值会进入死循环。

挖坑法

接下来，我们再看一下挖坑法的快速排序是如何实现的：

讲解

选数组左端点为key，用双指针准备从两端向中间移动。（选数组左端的值为key，则还是右指针先走。）

双指针移动，右指针遇小于或等于key值的填左坑，左指针遇大于或等于key值的填右坑，直到两个指针相遇。

指针相遇，key值填入相遇的位置。（key填入相遇的位置后别忘了更新key的索引位置）

接下来准备对key左右子数组分别进行重复的操作，与hoare的做法是一样的，进行递归排序。

代码

void swap(int* x, int* y) {int tmp = *x;*x = *y;*y = tmp;
}int hole(int* a, int left, int right)
{int keyIndex = left;int key = a[keyIndex];while (left < right){while (left < right && a[right] >= key) {--right;}a[left] = a[right];while (left < right && a[left] <= key) {++left;}a[right] = a[left];}a[right] = key;keyIndex = right;return keyIndex;
}void quickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;int keyIndex = hoare(a, left, right);quickSort(a, begin, keyIndex - 1);quickSort(a, keyIndex + 1, end);}

快慢指针法

讲解

接下来，我们再看一下快慢指针法的快速排序是如何实现的：

初始化数组左端元素为key，pre（慢指针）和cur（快指针）都向右移动。

遍历数组，当 cur 指向元素小于key时，pre向前移动一个位置，交换 cur 和 pre 位置的值（pre和cur所在的位置如果相同，就不用交换）；当cur指向元素大于或等于key，pre保持不动，cur继续往前走。

遍历结束后，交换 pre 位置的元素和key元素，然后更新key索引。

接下来准备对key左右子数组分别进行重复的操作，与hoare和挖坑法的做法是一样的，进行递归排序。

代码

void swap(int* x, int* y) {int tmp = *x;*x = *y;*y = tmp;
}int pre_cur(int* a, int left, int right)
{int keyIndex = left, pre = left, cur = left + 1;while (cur <= right){while (a[cur] < a[keyIndex] && ++pre != cur) {swap(&a[cur], &a[pre]);}++cur;}swap(&a[pre], &a[keyIndex]);keyIndex = pre;return keyIndex;
}void quickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;int keyIndex = pre_cur(a, left, right);quickSort(a, begin, keyIndex - 1);quickSort(a, keyIndex + 1, end);}

快排的时间复杂度与优化

我们前面讲了快速排序的三种写法，但其实三种写法的时间复杂度都差不多，只是第二种写法更好理解，第三种写法代码量少且不容易写错（因为在hoare和挖坑法版本的写法中，最内层的两个while循环有些细节问题需要注意）。所以总体来说更推荐第三中写法。

时间复杂度

在探讨快速排序算法时，我们注意到其递归展开图与二叉树结构有相似之处。为了深入理解其时间复杂度和最坏情况，我们可以从以下几个方面进行阐述：

1.时间复杂度分析

快速排序通过递归将数组不断划分，其递归深度与二叉树的深度相似。在理想情况下，递归深度最多为 logn，其中 n 是数组的长度。这是因为每次递归都将数组大致均匀地划分为两个子数组。

2.每层递归的工作量

在快速排序的每一层递归中，需要遍历当前子数组以定位key的最终位置。尽管随着递归的深入，之前的key元素不再需要考虑，但这对整体工作量的影响是有限的：

为了简化分析，我们可以假设每层递归都需要处理 n 个元素（尽管实际上这个数字会逐层减小，但减小的数量相对于 n 来说是可以忽略的）。

3.总体时间复杂度

结合上述两点，快速排序的总体时间复杂度为 O(n log n)。这是因为每层递归需要处理 n 个元素，而递归深度最多为 logn。

最坏情况分析

1.最坏情况的发生：

快速排序的最坏情况发生在数组已经接近排序完成（即顺序或逆序）时，或者key选择不当（如总是选择数组的第一个元素，而该元素恰好是最小值或最大值）时。

2.时间复杂度与栈溢出：

在最坏情况下，快速排序的时间复杂度可能达到 O(n²)。这是因为每次划分都极不均匀，导致递归深度接近 n，从而引发大量的递归调用和栈空间消耗，容易发生栈溢出。

3.key位置的影响：

key的位置对快速排序的性能至关重要。如果key总是选择接近数组的一端（如最小值或最大值），则划分将极不均匀，导致递归深度增加。
相反，如果key能够接近数组的中间位置，则划分将更加均匀，递归深度将更接近 logn，从而提高算法的效率。

对最坏情况的优化

当枢纽每次都接近数组的中间位置时，快速排序的递归展开图将更接近满二叉树。满二叉树的深度均匀，且每个节点都有两个子节点，这有助于减少递归调用的次数和栈空间的使用。因此，选择好的key策略（如随机选择、三数取中法等）对于提高快速排序的性能至关重要。

1.随机选择法

我们不一定让区间内第一个值作为key，我们每次在区间内随机选一个值做key。虽然随机选择的情况下也有可能选到当前区间内的最小值或最大值，但是那是一个低概率事件，大多数情况下还是不会取到区间内的最值。

代码：

void quickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//随机选keyint randIndex = left + (rand() % (right - left));swap(&a[left], &a[randIndex]);int keyIndex = pre_cur(a, left, right);if ((right - left + 1) > 10) {quickSort(a, begin, keyIndex - 1);quickSort(a, keyIndex + 1, end);}else {insertSort(a, right);}
}

2.三数取中

三数取中，将区间内的left、right和mid位置的值比较大小，取中间值。这种方法是一定不会取到区间内的最值，所以更推荐这种写法。

代码：

int getMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]) {if (a[mid] <= a[right]) {return mid;}else if (a[right] >= a[left]) {return right;}else {return left;}}else {if (a[left] <= a[right]) {return left;}else if (a[right] >= a[mid]) {return right;}else {return mid;}}
}void quickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//三数取中int midIndex = getMidIndex(a, left, right);swap(&a[left], &a[midIndex]);int keyIndex = pre_cur(a, left, right);if ((right - left + 1) > 10) {quickSort(a, begin, keyIndex - 1);quickSort(a, keyIndex + 1, end);}else {insertSort(a, right);}
}

小区间优化

在快速排序算法中，当处理小规模数据时，递归调用可能会变得低效。为了优化这种情况，我们可以引入小区间优化策略。

背景

1.递归调用的低效性：在快速排序中，当数组被划分成较小的子数组时，递归调用可能会变得频繁且低效。特别是当子数组的长度非常小（如只有几个元素）时，递归调用的开销可能会超过直接排序这些元素所需的开销。

2.插入排序的优势：插入排序在处理小规模数据时通常表现较好。当数据已经部分有序或数据量很小时，插入排序的效率往往高于快速排序的递归调用。

原理

1.设定阈值：为了避免在小规模数据上进行不必要的递归调用，我们可以设定一个阈值（通常取10左右）。当子数组的长度小于这个阈值时，我们不再使用快速排序的递归调用，而是改用插入排序来排序这些元素。

2.优化二叉树结构：在快速排序的递归过程中，二叉树的深度和形状对算法的效率有很大影响。当子数组长度较小时，递归调用会生成大量的浅层节点，这些节点的处理开销较大。通过设定阈值并使用插入排序，我们可以减少这些浅层节点的数量，从而优化二叉树的结构，提高算法的整体效率。

3.利用插入排序的优势：插入排序在处理小规模或部分有序数据时非常高效。当子数组长度小于阈值时，这些子数组很可能已经部分有序（特别是在快速排序的后期阶段），因此插入排序能够更快地完成排序任务。

为什么阈值取10左右？

经验值：通过大量的实验和观察，人们发现当子数组长度小于10时，使用插入排序通常比继续递归调用快速排序更高效。这个阈值是一个经验值，但在大多数情况下都能取得良好的效果。
平衡效率与开销：选择10作为阈值是为了在效率（即排序速度）和开销（即递归调用的额外负担）之间找到一个平衡点。当子数组长度小于10时，递归调用的开销开始变得显著，而插入排序则能够更高效地处理这些小规模数据。
优化二叉树深层节点：通过设定阈值并使用插入排序，我们可以优化二叉树中深层节点的处理。这些节点通常对应着较小的子数组，使用插入排序能够减少不必要的递归调用，从而提高算法的整体效率。

代码

void quickSort(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//随机选key/*int randIndex = left + (rand() % (right - left));swap(&a[left], &a[randIndex]);*///三路取中int midIndex = getMidIndex(a, left, right);swap(&a[left], &a[midIndex]);int keyIndex = pre_cur(a, left, right);if ((right - left + 1) > 10) {quickSort(a, begin, keyIndex - 1);quickSort(a, keyIndex + 1, end);}else {//小区间优化insertSort(a, right);}
}

非递归版本

递归版本的快速排序有一个问题：递归的深度太深容易栈溢出。

思路

非递归版本的快速排序需要借助栈来实现。其实在递归版本的快速排序中，每一次递归中变化的主要是区间的大小，所以我们可以在每次单趟排序完后，让对应区间的子区间入栈。

具体步骤

1.初始化栈并推入初始索引

创建栈，将数组的起始和结束索引入栈：

2.开始循环处理栈顶元素

弹出栈顶的左右索引，确定当前子数组的范围。

这里需要注意，在入栈的时候，如果先入栈的是end，然后再入栈begin，那先出栈的就是begin，后出栈的就是end。（先进后出）

调用划分函数（即前面讲hoare版本的hoare函数、挖坑法的hole函数、快慢指针的pre_cur函数），获取key元素的位置：

根据key元素位置，将未排序的子数组索引范围入栈：

（如果子区间只有一个值或者没有值就不入栈）

重复2的步骤，直至栈为空，则排序完成。

3.最后销毁栈。

代码

void quickSortNonOrder(int* a, int n)
{st s;initStack(&s);int begin = 0, end = n - 1;pushStack(&s, end);pushStack(&s, begin);while (!isEmpty(&s)){int left = stackTop(&s);popStack(&s);int right = stackTop(&s);popStack(&s);int keyIndex = pre_cur(a, left, right);if (keyIndex - 1 > left) //左子区间的右端索引大于左端索引说明这个子区间不止一个值，就可以入栈{pushStack(&s, keyIndex - 1);pushStack(&s, left);}if (keyIndex + 1 < right) //右子区间的右端索引大于左端索引说明这个子区间不止一个值，就可以入栈{pushStack(&s, right);pushStack(&s, keyIndex + 1);}}destroyStack(&s);
}

这里的栈会用到前面讲解栈的代码：数据结构--栈和队列-CSDN博客